基于风速估计的风力机状态反馈滑模容错控制

马磊明 ,肖玲斐 ,姜 斌

(1.南京航空航天大学自动化学院,江苏南京 210016;2.南京航空航天大学能源与动力学院,江苏南京 210016)

1 引言

近年来,风能作为一种清洁环保的可再生能源发展迅速.伴随着风机装机总量的提升,风力机的几何结构也在不断扩大,这就会造成控制难度增加和故障多发[1].故障在增加发电成本的同时,亦会导致风力机失去竞争力.

风力机的高精度控制依赖于精确的风速信息.目前,风速测量方法主要有传统的风速传感器和无传感器风速测量.由于传统风速传感器自身的机械结构和设计过程比较复杂且测量精度低等不足,很难保证风速实时准确测量.特别是在低风速地区,大惯性矩的接触式风速传感器对低风速不敏感.因此,如何获得一个成本低且效果好的风速估计方案已经成为风力机控制策略设计的关键问题.近来,无传感器风速测量成为解决这一问题的有效手段[2–8].已有文献中风速估计方法包括基于神经网络的风速估计[2–3]、基于Newton Raphson的风速估计[4]、基于未知输入的风速估计[5]、基于滤波器的风速估计[6]、基于统计模型的风速估计[7]和基于数据融合的风速估计[8]等.

文献[2]采用基于遗传算法的支持向量机模型,将功率、桨距角和转速等物理可测量信号作为输入对有效风速进行估计.文献[3]提出一种用于风速估计的无传感器控制方案,通过基于高斯径向基函数神经网络的非线性映射近似风力机的空气动力特性.文献[4]提出一种由自适应Kalman滤波器和Newton Raphson算法组成的有效风速估计方法,自适应Kalman滤波器可以实现对测量和过程噪声的估计.文献[8]分析了风速计的测量频谱和风力机功率的关系,并利用信号频域互补特性设计了有效的风速估计器.显然,上述方法需要精确的数学模型或较高的运算成本,这大大限制了其在实践中的应用.神经网络由于计算量小、计算精度高、求解速度快且易于实现等优点得到了广泛的应用.本文采用基于变速灰狼优化(variable speed grey wolf optimization,VGWO)算法的组合径向基函数神经网络(combined radial basis function neural network,CRBFNN)对风速有效值进行估计,可以改善风速测量精度并提高控制系统可靠性.

提高风力机运行可靠性一直是风力发电领域研究的关键问题,直接决定风力发电能否成为满足世界电力需求的主要动力之一.风力机发生故障是不可避免的,尤其是对于在恶劣的环境中运行的大型风力机.针对上述问题,在过去的十年中,风力发电领域的容错控制技术已得到广泛研究,极大提高了风力机的可靠性、可用性和安全性[9–16].风力机常见的容错控制方法包括T-S模糊观测器[9]、滑模控制[10]、扩展状态观测器[11]、鲁棒控制[12]、数据驱动[13]、模型预测控制[14]、模型参考自适应[15]和Kalman滤波器[16]等.

文献[9]针对受执行机构故障影响的风力机,提出了一种基于模糊观测器的容错控制方案.控制目标是要确保风力机转速跟踪给定参考转速,免受执行机构故障影响.文献[10]利用广义滑模观测器设计容错控制策略,可以同时补偿执行机构和传感器故障.文献[13]设计了一种基于数据驱动的容错控制系统,其核心是将基于奇偶矢量构造的残差生成器嵌入到控制回路中,并提出了一种优化方案用于选择对特定变量敏感的奇偶校验矢量.文献[14]提出了具有模型预测补偿的分层容错控制器,包括全局模型预测控制和监督控制.结果表明,所提控制器在发生故障时可以获得更平滑的发电机转矩和桨距角输入.在上述容错控制方法中,滑模控制由于能够克服系统不确定性,对于扰动和未建模动态具有强鲁棒性而得到广泛的应用和研究.本文设计了自适应状态反馈滑模容错控制(adaptive state feedback sliding mode fault tolerant control,AFSMFTC)策略,所提策略包含状态反馈和全阶补偿,具有较强的容错控制能力.

2 风力机模型

风力机主要由3个部分组成,包括风轮(由叶片、轮毂和变桨距系统组成),传动系统(由主轴、齿轮箱和制动器组成)和发电机.风力机结构如图1所示,本节分别对风轮模型和传统系统模型展开介绍.

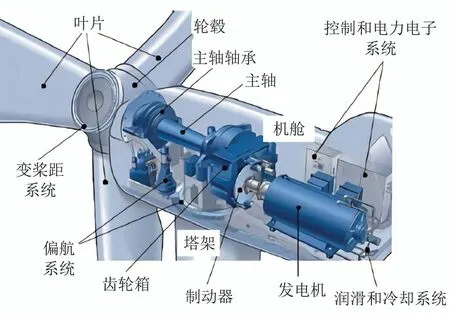
图1 风力机结构[17]Fig.1 Typical structure of wind turbine[17]

2.1 风轮模型

风力机叶尖速比λ为

式中:R是风轮半径,单位为m;v是来流风速,单位为m/s;ωr是风轮转速,单位为rad/s.

风力机风轮输出功率Pa满足如下关系:

式中:SA是风轮扫掠面积,单位为m2;ρ是空气密度,单位为kg/m3;Pa为风轮输出功率,单位为W;Cp是风力机功率系数,代表风轮从风能中吸收功率的能力,可表示为[18]

式中:λi用于简化公式,不代表任何风力机的物理参数,满足

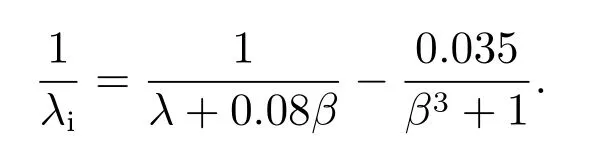
图2展示了叶尖速比λ,桨距角β和风能利用系数Cp的关系.由图可知,风能利用系数Cp对叶尖速比λ和桨距角β的变化规律.当桨距角β维持不变时,随着叶尖速比λ变化,风能利用系数Cp能获得最大值.

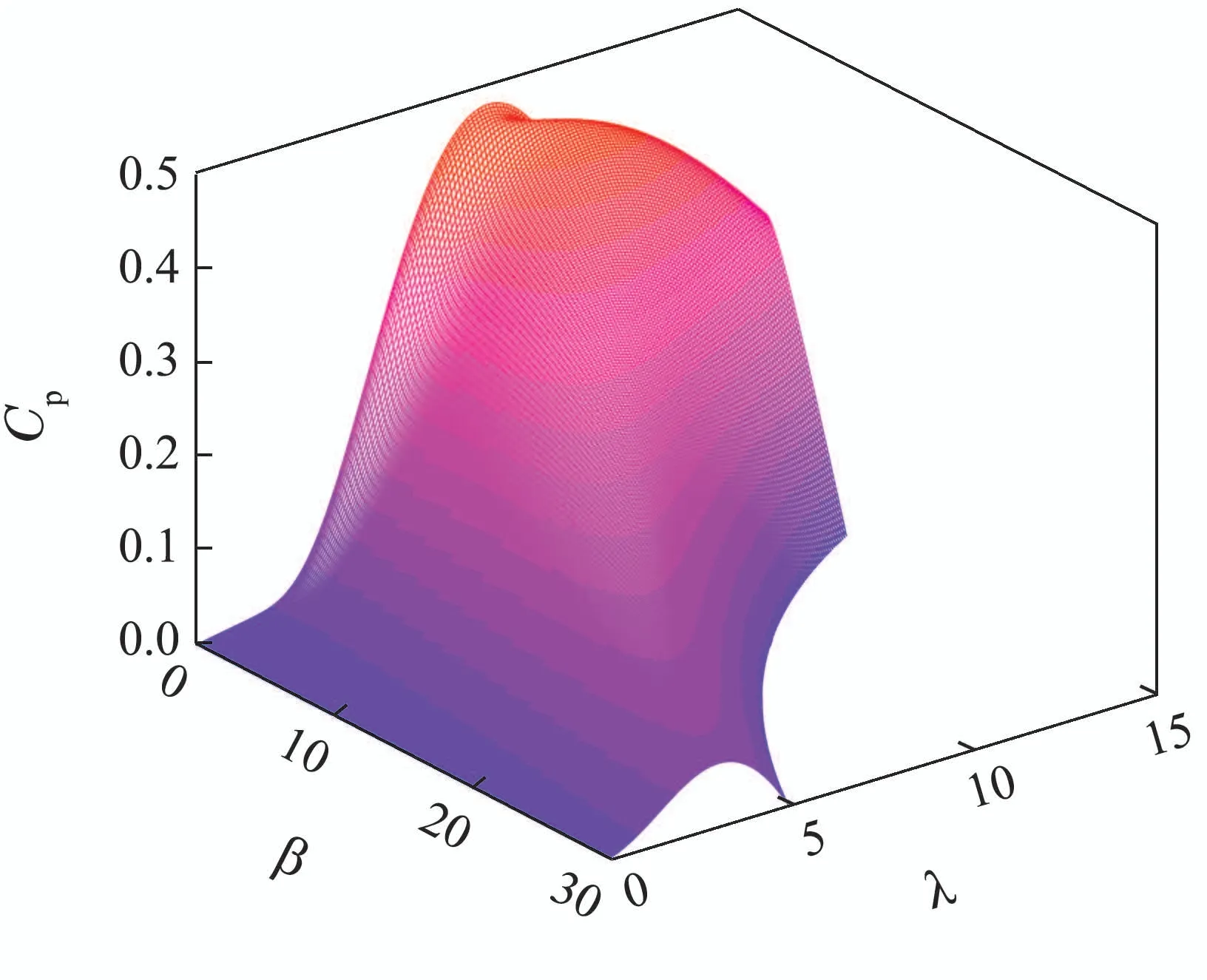
图2 功率系数曲线[19]Fig.2 Power coefficient curve[19]

2.2 传动系统模型

传动系统主要由风轮、低速轴、齿轮箱、高速轴和发电机转子组成,如图3所示.

图3 传动系统模型Fig.3 Model of transmission system

研究表明,两质量块的刚性模型能很好地满足动力学分析的需要.本文建立风力机传动系统模型如下[20–21]:

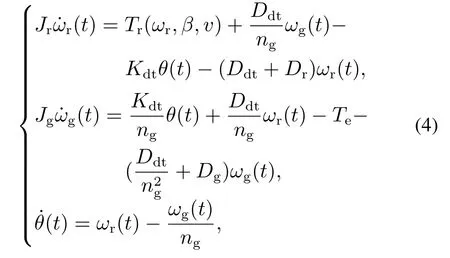
式中:Jr是风轮转动惯量,单位为kg·m2;Jg是发电机转动惯量,单位为kg·m2;ωg是发电机角速度,单位为rad/s;ng是传动比;θ是扭角,单位为rad;Kdt是扭转刚度,单位为Nm/rad;Ddt是扭转阻尼,单位为Nm·s/rad;Te是发电机转矩,单位为Nm;Tr是风轮转矩,单位为Nm;Dr是转子侧轴承摩擦阻尼系数,单位为Nm·s/rad;Dg是发电机侧轴承摩擦阻尼系数,单位为Nm·s/rad.

2.3 风力机线性化模型

令x(t)=[θ(t)ωg(t)ωr(t)]T,u(t)=β和d(t)=.其中,是风速估计值.将风力机模型(4)在稳态点x0处展开可得风力机的线性化模型

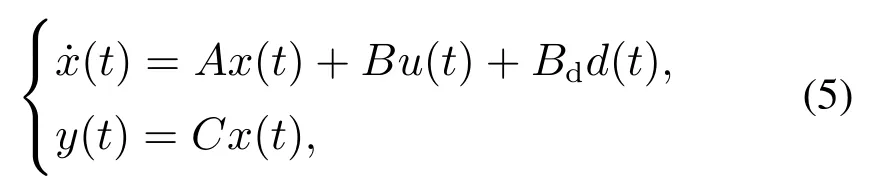
式中:x(t)是状态变量;u(t)是输入量;y(t)是输出量;d(t)是外部扰动即风速;且系数矩阵A,B,C和Bd分别满足

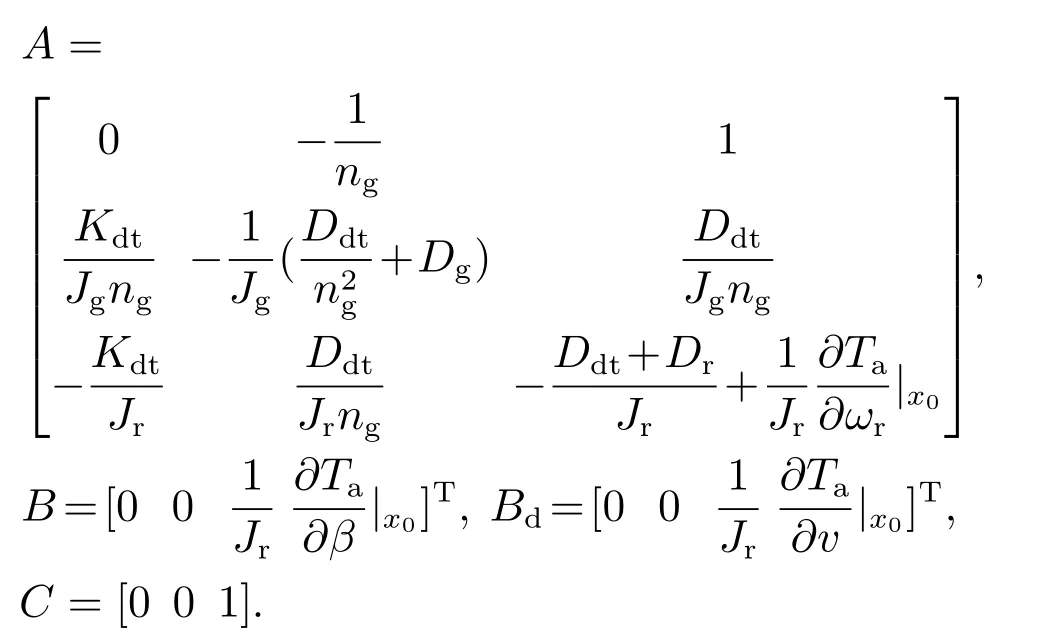
假设1外部扰动d(t)满足∥d(t)∥≤Hb,其中Hb是已知正常数.

假设2Rank(CB)=Rank(B)成立.

2.4 线性化故障模型

当非极端故障出现在变桨距执行机构中,控制输入uFault(t)可表示为

式中ρ(t)是执行机构故障因子.

3 自适应状态反馈控制器设计

本文所设计的滑模容错控制律结合了积分滑模理论和自适应增益.积分滑模控制律包含系统的状态反馈信息和全阶补偿输入,所提自适应状态反馈控制原理如图4所示.

图4 自适应状态反馈控制器原理图Fig.4 Principle of AFSMFTC

3.1 滑模面与滑模控制器

定义与状态相关的滑模面S(t)如下所示:

式中:矩阵G满足GCB矩阵可逆;补偿量l(t)由全阶补偿器确定;x(0)代表初始状态.

对式(7)求导可得

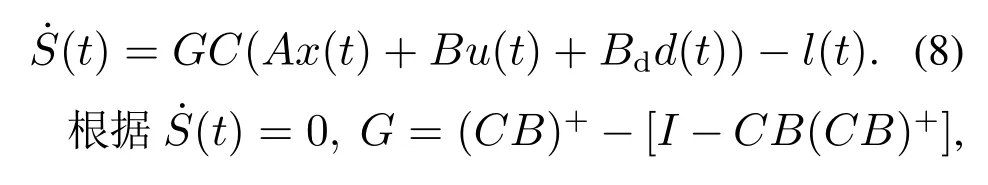
将式(9)代入式(5)可得

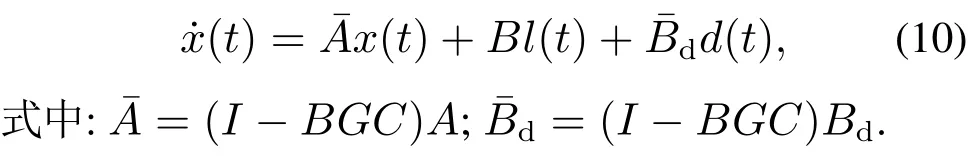
3.2 全阶补偿器

定义矩阵U=−B(CB)++Y(I −CB(CB)+),其中,Y是任意矩阵.进而定义矩阵M=I+UC,H=L(I+CU)−MAU,其中,L是增益矩阵.

根据假设2,可得MB=0,则补偿量l(t)可由全阶补偿器获得

式中:ξ是辅助变量;K是增益矩阵.

定义误差向量e(t)=Mx(t)−ξ(t),进而可得

式中Tx=MA −HC −MAM+LCM,且满足

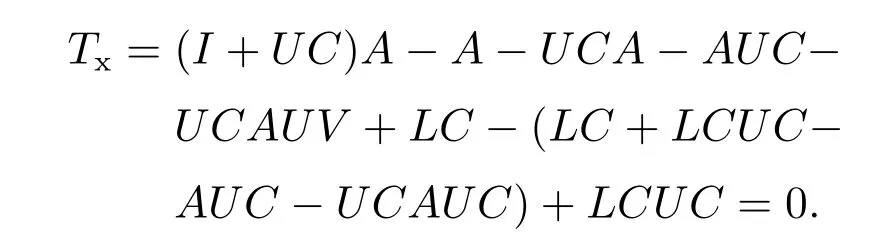
则式(12)可重写为

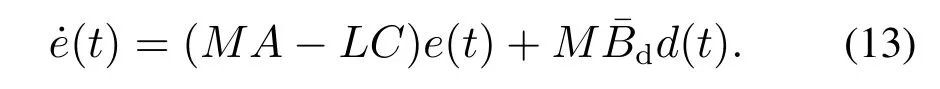
结合式(11)可得

定理1对于给定的µ>0,如果存在矩阵Px>0,Pe>0和K满足矩阵不等式(15),则滑动模态(10)渐近稳定.

证选取Lyapunov函数为

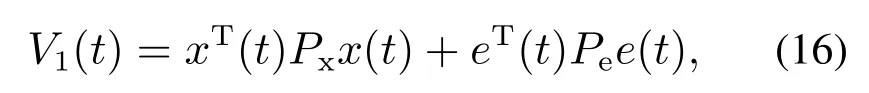
式中Px和Pe为正定矩阵.

对式(16)求一阶微分可得

式中Υ满足

将Υ放大为σ如下:

如果σ <0,则有

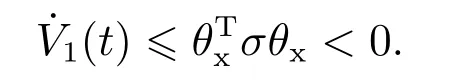
式(17)中存在3个矩阵变量,分别为Px,Pe和K.这3个矩阵变量是以非线性的形式出现在矩阵不等式中.因此,要直接从式(17)中求解Px,Pe和K是很困难的.需要将式(17)转化为线性矩阵不等式(linear matrix inequality,LMI)进行求解,补充以下引理:

引理1(Schur补引理) 对给定的对称矩阵SF满足[22]

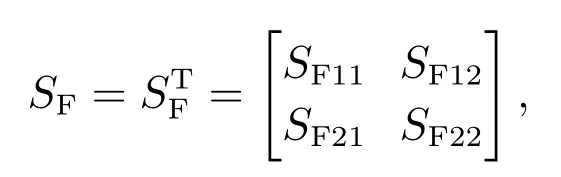
式中SF11和SF22是方阵,则以下条件等价:

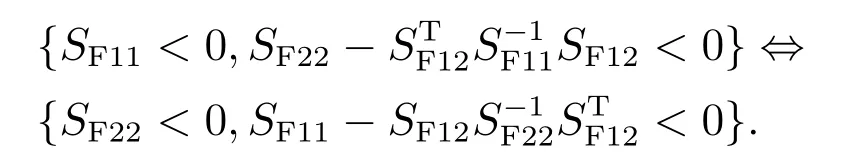
引理2给定具有适当维数的矩阵Θ=ΘT,Γ和Ψ,则Θ+ΓΛ(t)Ψ+ΨTΛT(t)ΓT<0.对所有满足ΛT(t)Λ(t)≤I的Λ(t)都成立的充分必要条件是存在一正数Ψ >0使得下式成立[23–24]:

根据式(17)可得

进一步对式(18)进行简化可得

3.3 自适应状态反馈控制器

自适应状态反馈滑模控制律u(t)设计如下:

式中:ε是正的切换增益;是自适应律,且满足

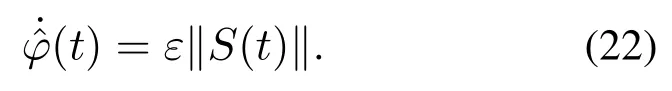
定理2若控制律满足式(21)且自适应律满足式(22),则系统状态(5)渐近稳定.

证选取Lyapunov函数为

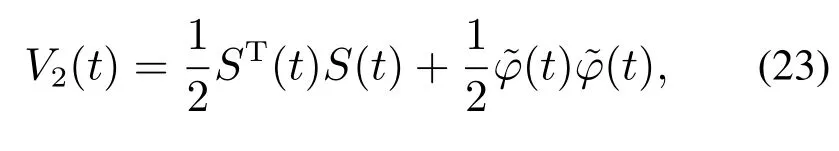
对式(23)求导可得

已知κ>0,则闭环系统渐近稳定.证毕.

4 基于VGWO的CRBFNN风速估计

针对传统风速传感器风速测量精度低的问题,本文利用改进的VGWO算法对CRBFNN权值进行寻优,结合了VGWO算法收敛速度快、求解精度高和全局搜索能力强和CRBFNN全局拟合精度高的优点,进而改善风速估计效果.其原理如图5所示.

图5 基于VGWO的CRBFNN风速估计Fig.5 Wind speed estimation based on VGWO–CRBFNN

神经网络被广泛应用于系统辨识和控制器设计[25].与BP神经网络相比,径向基函数神经网络结构更简单且学习速度更快[26].径向基函数神经网络的基函数包括高斯基函数、立方基函数、多重二次和反多重二次基函数.本文采用的基函数是具有良好非线性拟合能力的高斯基函数和具有良好线性拟合能力的立方基函数组合.改进后的神经网络称为组合径向基函数神经网络.本文利用已有的风力机输入和输出数据,对风力机的等效模型进行辨识,如图5所示.神经网络训练所需的风速v、发电机转矩Te和风轮转速ωr数据来源于美国可再生能源国家实验室[27].测试过程中,将Te和ωr作为输入量,将风速估计值作为输出量.组合径向基函数神经网络的总体输入输出映射关系如下所示:

式中:xR=[ωrTe]T表示神经网络输入向量;表示神经网络输出向量;bm是隐含层的第m个中心单元;h是神经单元数;vm是介于隐含层和输出层的权重系数;nm是基函数的宽度;∂1和∂2是权重系数.

此外,本文利用VGWO算法对CRBFNN权值寻优.思路是将PSO算法的速度和位置分量引入到GWO算法中形成VGWO算法,结合了GWO算法局部搜索能力强的优点[28]和PSO算法全局搜索能力强的优点.并设计如下目标函数:

式中:ev表示风速估计误差,满足ev=其中,GWO算法步骤如下:

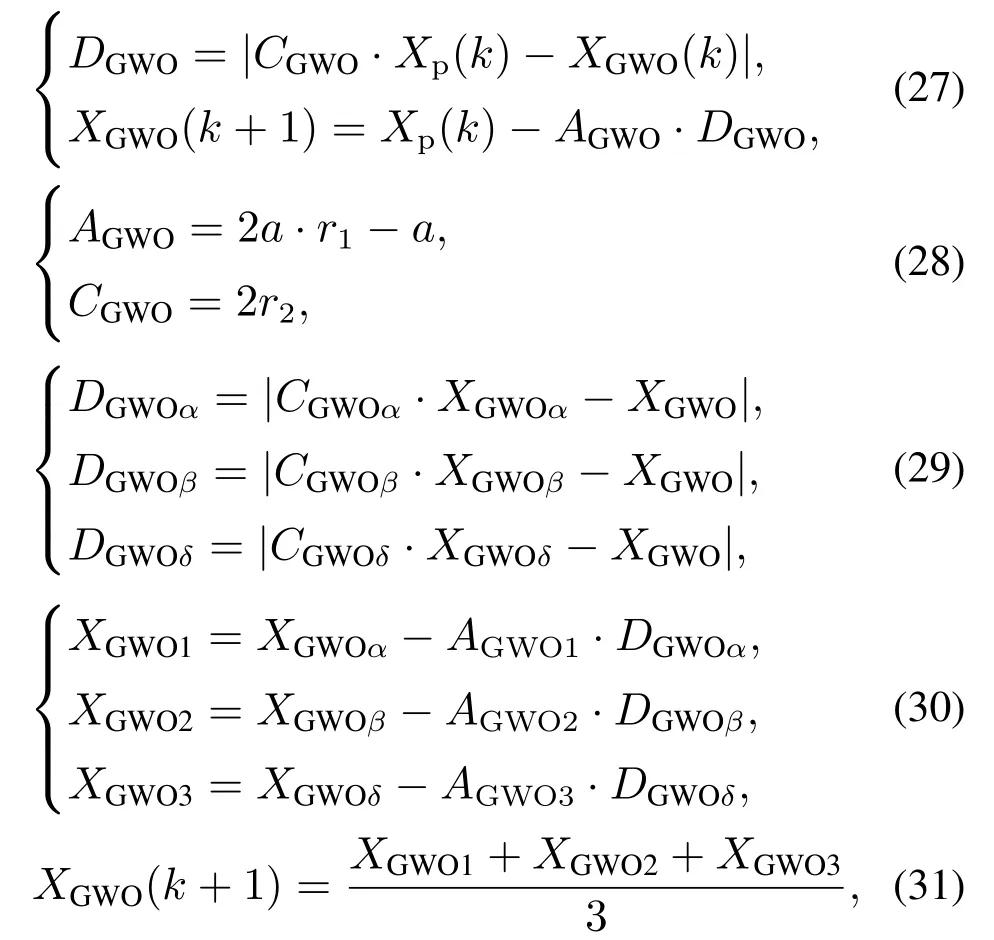
式中:k是迭代次数;AGWO和CGWO是系数向量;Xp是猎物所在的位置;XGWO是灰狼所在的位置;DGWO是灰狼与猎物之间的距离;控制参数a在范围[0,2]内线性变化;r1和r2是在范围[0,1]内变化的随机向量;XGWOα,XGWOβ和XGWOδ分别是灰狼αGWO,βGWO和δGWO当前所在的位置;CGWOα,CGWOβ和CGWOδ是算法系数;DGWOα,DGWOβ和DGWOδ分别是灰狼αGWO,βGWO和δGWO与猎物之间的距离;XGWO1,XGWO2和XGWO3分别是灰狼ωGWO相对于αGWO,βGWO和δGWO的前进向量;AGWO1,AGWO2和AGWO3分别是算法系数.融合后的速度vi和位置xi分量更新公式如下所示:

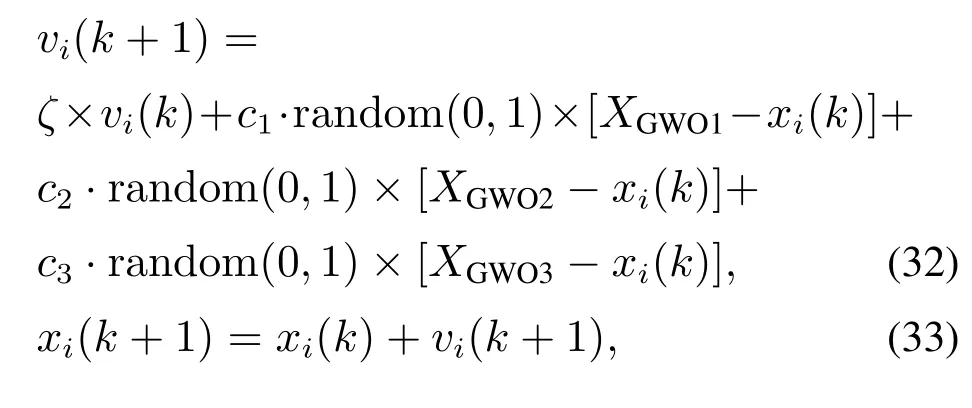
式中:c1,c2和c3是学习因子;ς是惯性因子.

5 仿真分析

为了验证所提容错控制策略的有效性和优越性.本节从4个方面进行仿真.首先,针对基于VGWO算法的CRBFNN风速估计进行仿真;其次,分别在无故障和突变故障状态下对所提AFSMFTC策略和基于线性二次型调节器的干扰抑制控制器(disturbance rejection controller based on linear quadratic regulator,LQR–DRC)进行仿真;最后,对两种控制策略进行对比.风力机参数如表1所示.

表1 8 MW风力机参数Table 1 Parameters of 8 MW wind turbine

由于文献[29]中通过比较LQR–DRC与PID验证了LQR–DRC策略有效性,因此本文仅与LQR–DRC进行仿真对比,LQR–DRC原理如图6所示.

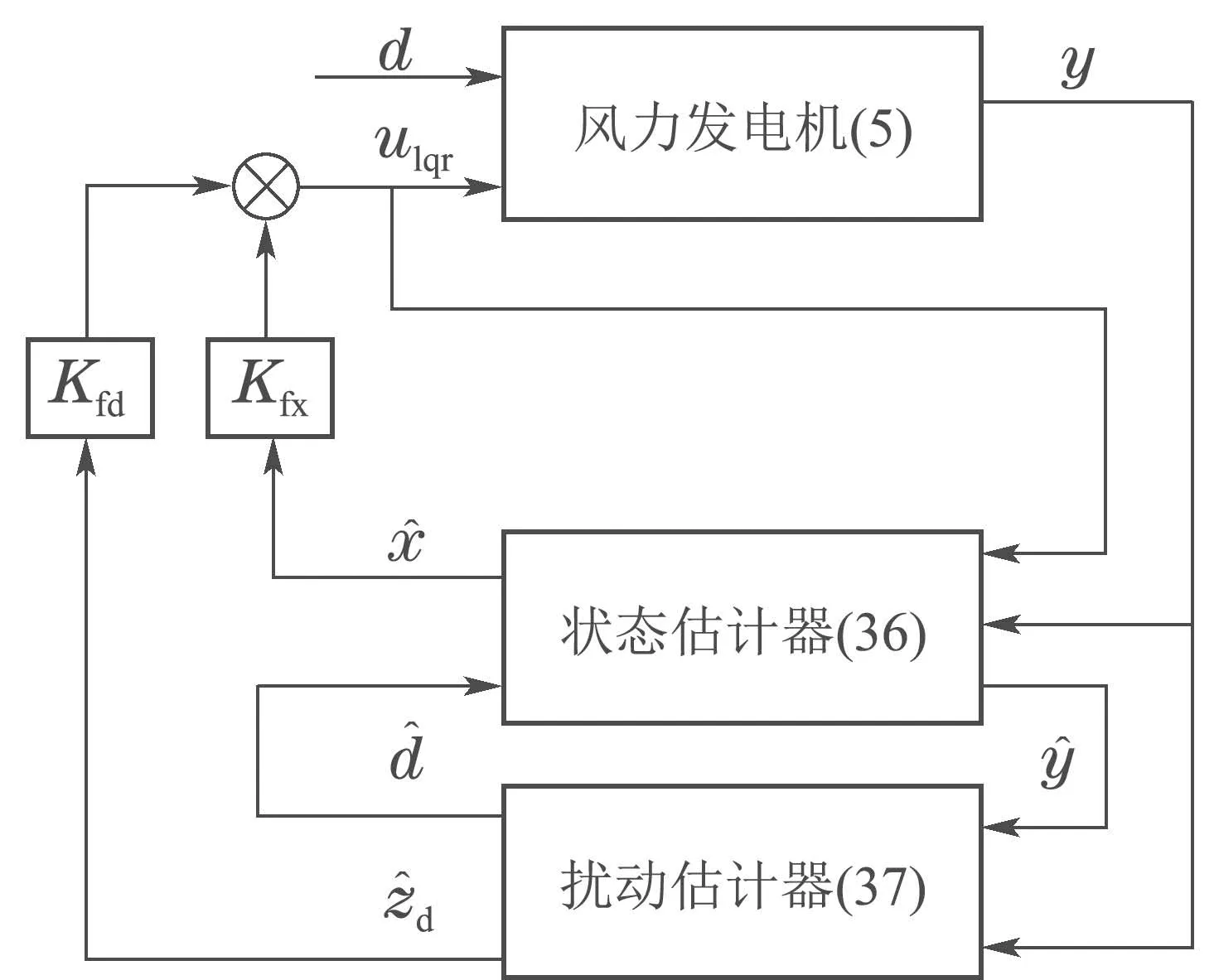
图6 LQR–DRC原理图Fig.6 Principle of LQR–DRC

反馈控制律ulqr设计为

式中:Qx是半正定对称矩阵;Ru是正定对称矩阵.

设计状态估计器如下:

设计扰动估计器如下:

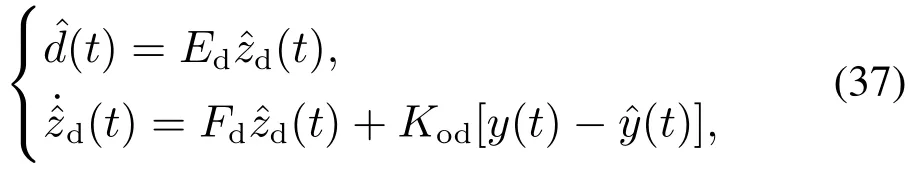
式中:Kox是状态估计矩阵;Kod是扰动估计矩阵;zd是扰动状态量;Ed和Fd是已知的扰动系数矩阵.

5.1 风速估计仿真

为了测试并验证所提出VGWO算法的性能,文献[19]分别对GWO算法,PSO算法和VGWO算法的参数优化性能进行对比.结果表明,所提VGWO算法能获得最小的适应度函数值,具有更快的寻优速度和更高的寻优精度.风速估计仿真如图7所示,结果表明基于VGWO算法的CRBFNN风速估计具有更高的观测精度和更好的跟踪性能.

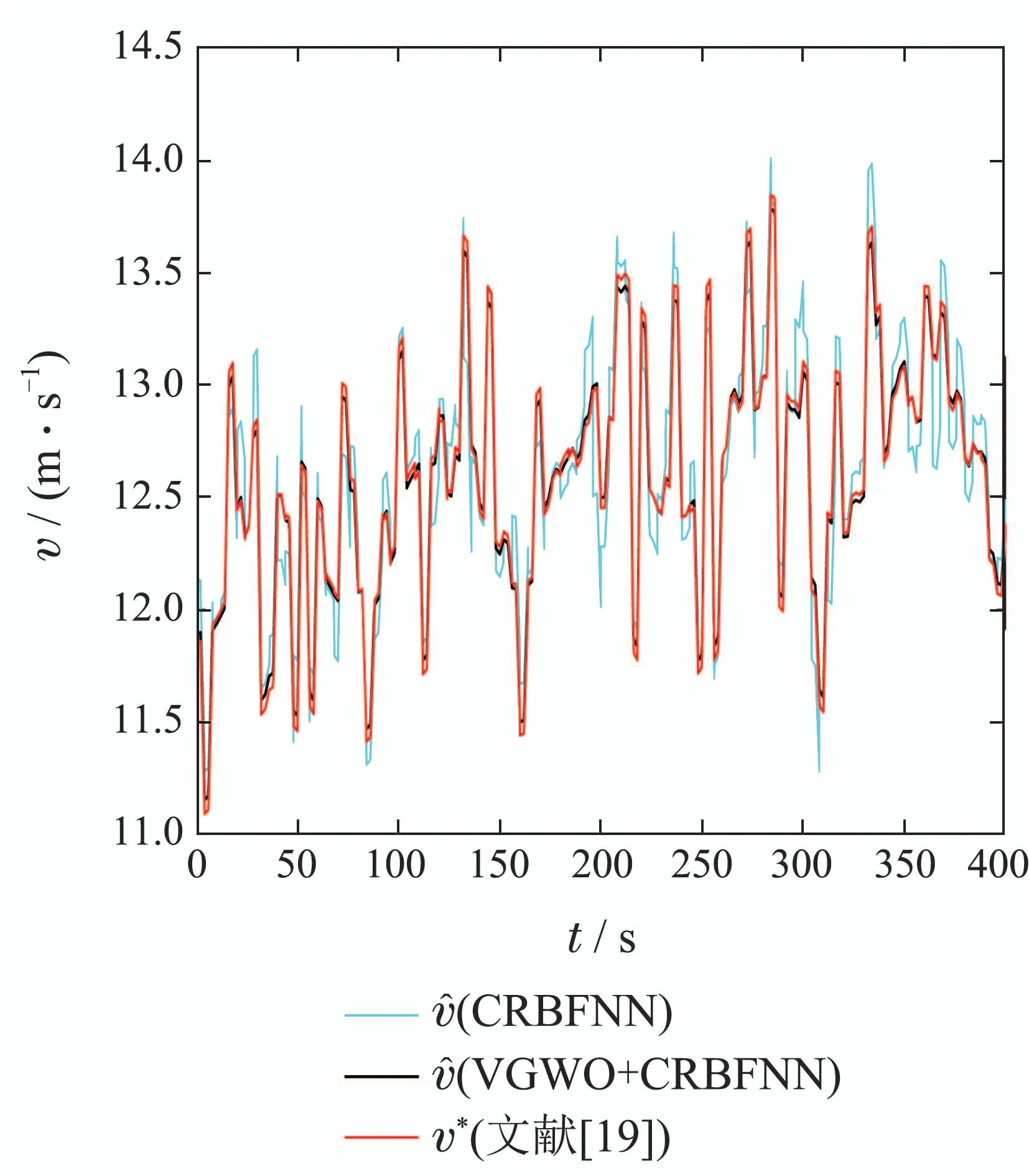
图7 风速估计曲线Fig.7 Wind speed estimation curves

5.2 无故障仿真

5.2.1 AFSMFTC策略无故障仿真

图8展示了全阶补偿器输入的变化情况.可以看出,随着风速变化,全阶补偿器在及时的调节以对控制量进行补偿.

图8 全阶补偿器输入(无故障)Fig.8 Full order compensator input(without fault)

5.2.2 LQR–DRC策略无故障仿真

图9和图10分别展示了风速与估计和风轮转速与估计的变化情况.可以看出风速估计误差和风轮转速估计误差分别为0.130%和0.006%.这表明LQR–DRC策略具有较高的观测精度.

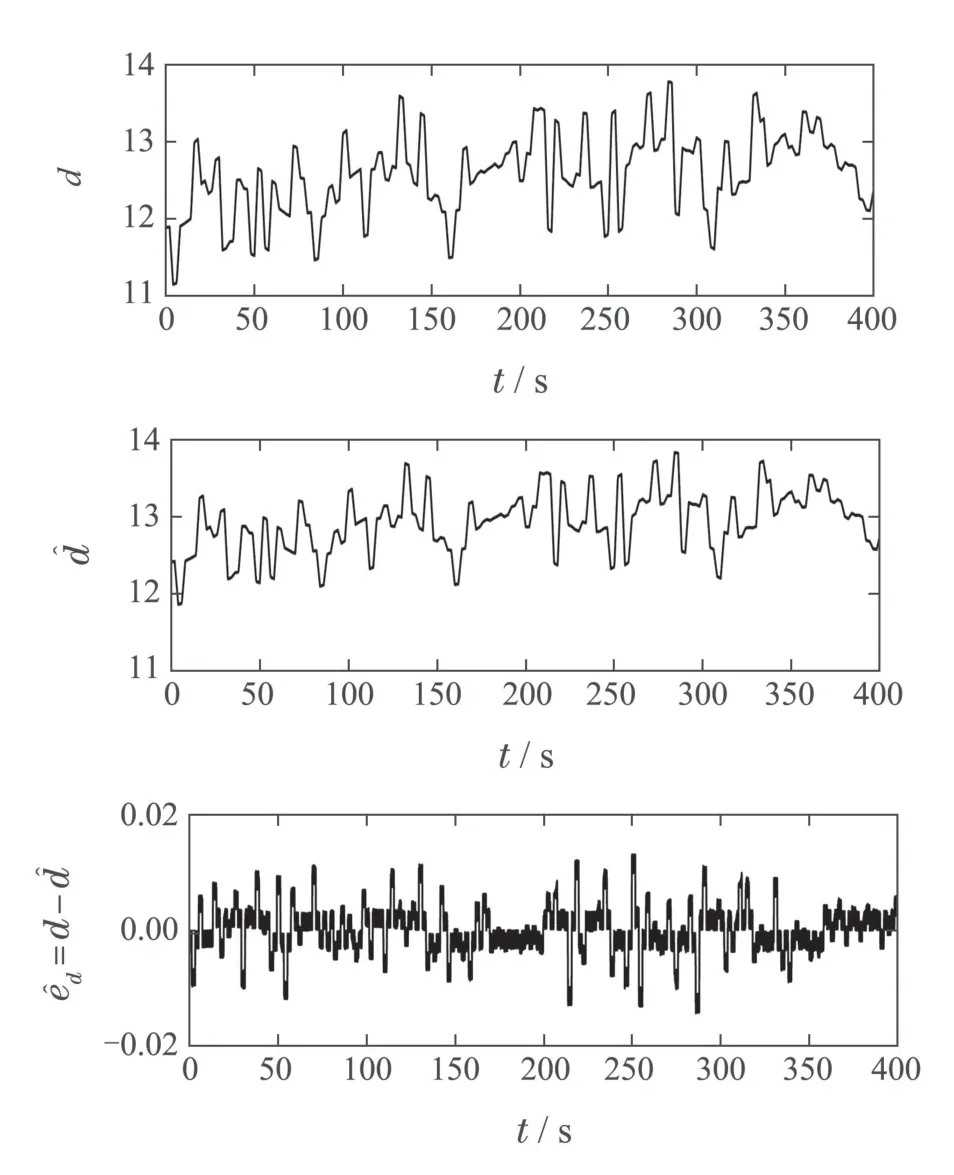
图9 风速与估计(无故障)Fig.9 Wind speed and estimation(without fault)

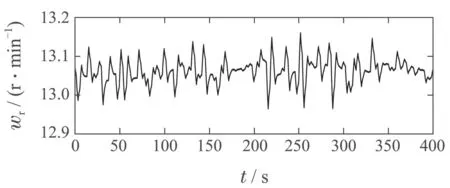
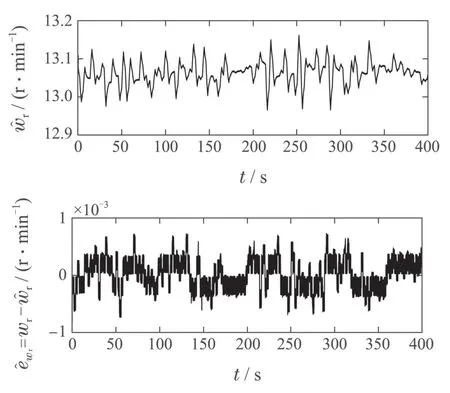
图10 风轮转速与估计(无故障)Fig.10 Rotor speed and estimation(without fault)

5.3 有突变故障仿真

5.3.1 AFSMFTC策略有突变故障仿真

为了验证AFSMFTC策略的容错能力,在仿真时间180 s处施加持续时间为1 s的突变故障,如图11所示.可以看出,与无故障仿真相比,所提AFSMFTC控制策略能及时对故障进行容错控制.

图11 全阶补偿器输入(有突变故障)Fig.11 Full order compensator input(with abrupt faults)

5.3.2 LQR–DRC策略有突变故障仿真

图12–13分别展示了基于LQR–DRC的有突变故障仿真结果,可以看出,LQR–DRC策略的风速估计误差和风轮转速估计误差分别增加了0.029%和0.009%.这表明LQR–DRC策略容错能力较差.

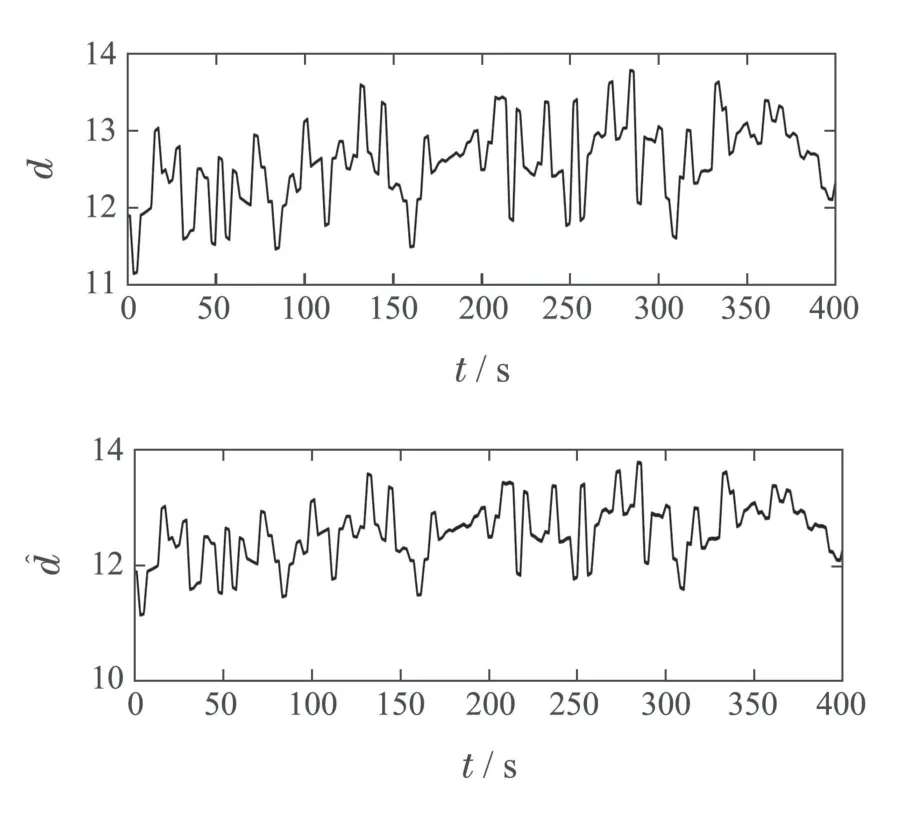
图12 风速与估计(有突变故障)Fig.12 Wind speed and estimation(with abrupt faults)

图13 风轮转速与估计(有突变故障)Fig.13 Rotor speed and estimation(with abrupt faults)

5.4 控制器对比仿真

5.4.1 无故障对比仿真

在无故障情况下,所提AFSMFTC策略产生的抖振小于LQR–DRC.分别将风轮转速、桨距角和输出功率控制效果对比可知,所提控制容错策略有更高的跟踪精度、更小的抖振和更短的收敛时间,这对风力机长久运行和降低疲劳载荷十分有利.

表2是对无故障仿真图14–16数据的进一步分析处理,其中Max(·),Min(·),Mean(·)和STDEV(·)分别代表最大值、最小值、平均值和标准偏差.通过多维度的数据分析处理,可以直观的看出所提算法具有维持风力机平稳运行的优势.

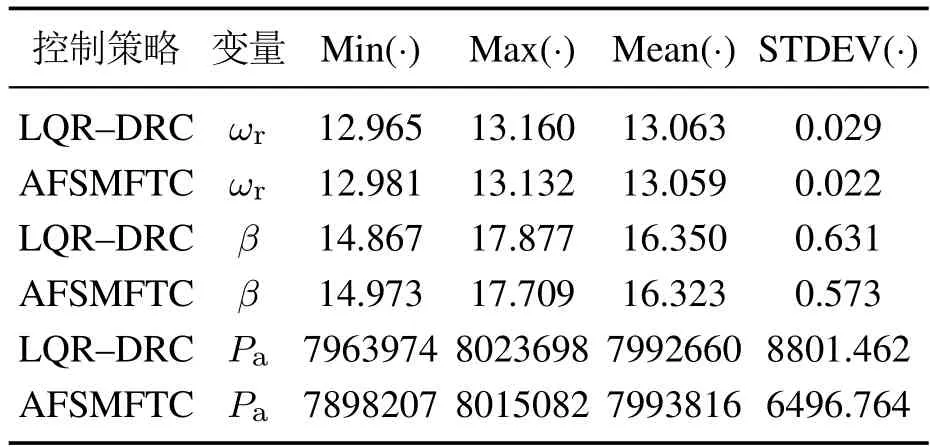
表2 无故障控制性能对比Table 2 Control performance comparison without fault

图14 风轮转速对比(无故障)Fig.14 Comparison of rotor speed(without fault)

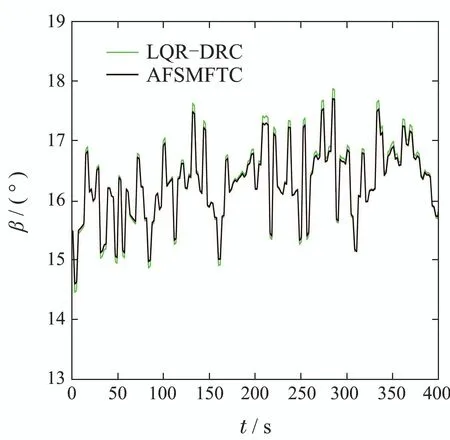
图15 桨距角对比(无故障)Fig.15 Comparison of pitch angle(without fault)

图16 输出功率对比(无故障)Fig.16 Comparison of power(without fault)

5.4.2 有突变故障对比仿真

根据图17–19可知,在风力机存在执行机构突变故障的情况下,考虑AFSMFTC策略作用的风力机主要运行参数波动范围更小,表现出较强的容错性能和鲁棒性,这对于风力机长期平稳运行非常重要.

图17 风轮转速对比(有突变故障)Fig.17 Comparison of rotor speed(with abrupt faults)

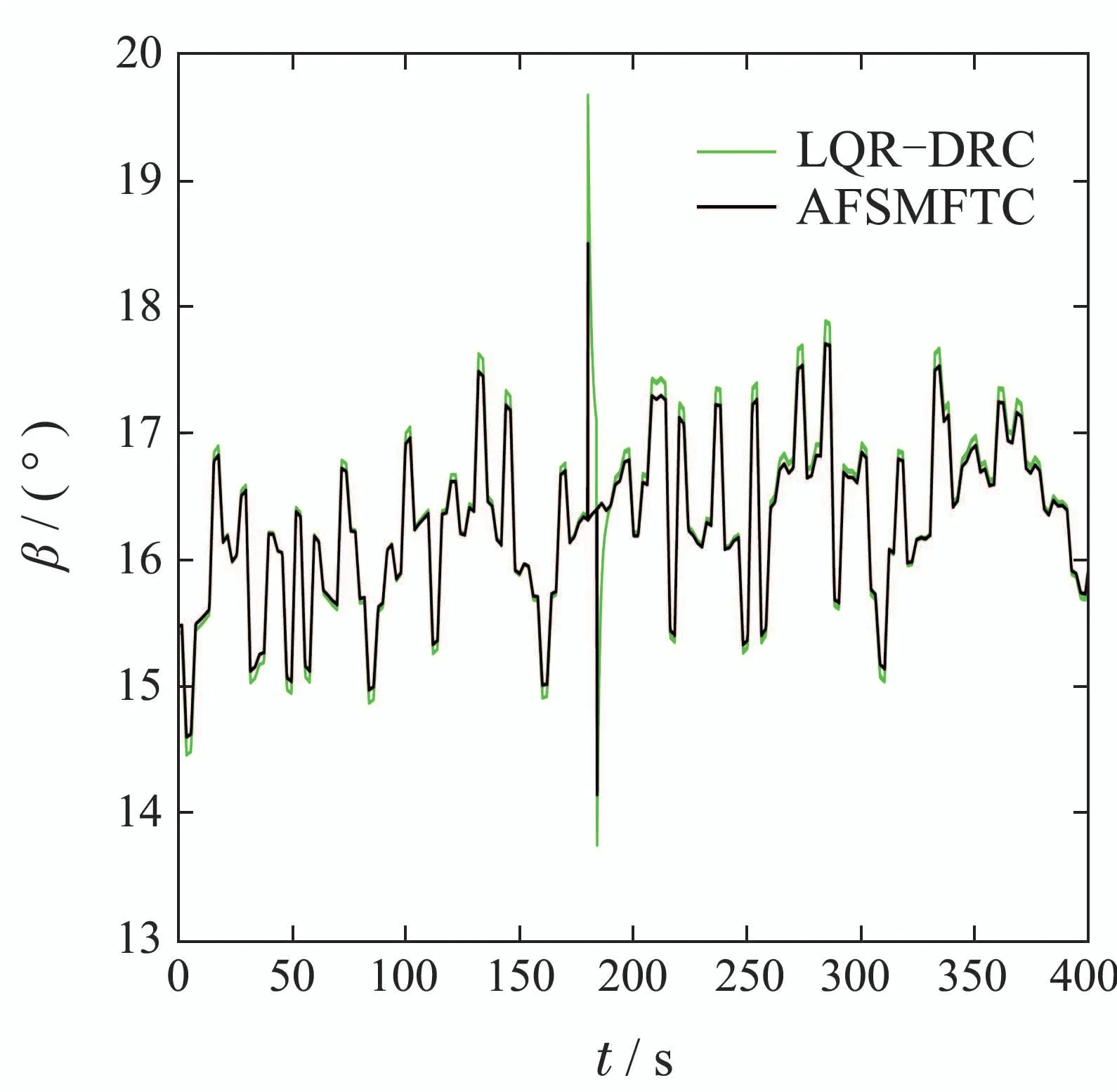
图18 桨距角对比(有突变故障)Fig.18 Comparison of pitch angle(with abrupt faults)

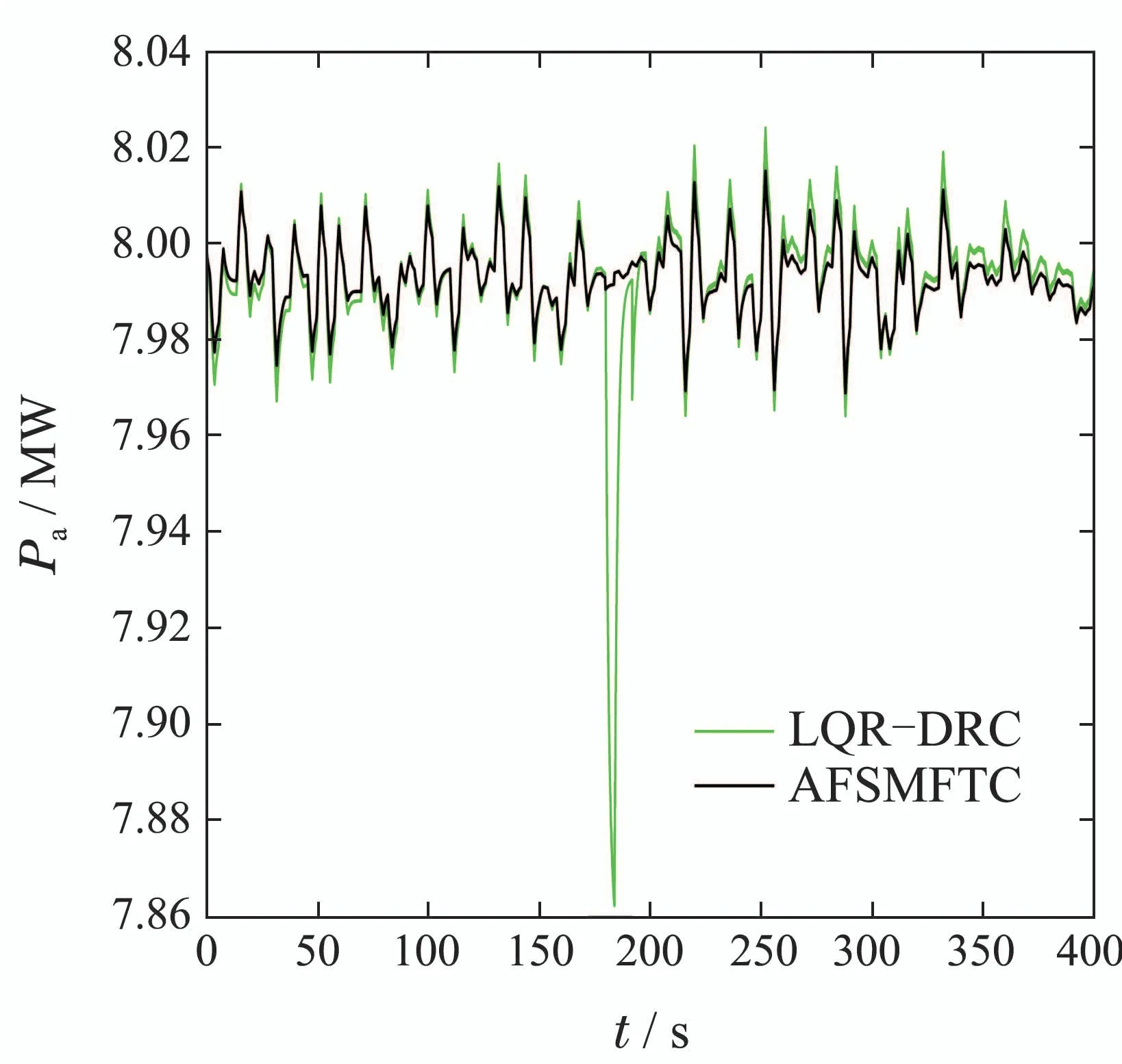
图19 输出功率对比(有突变故障)Fig.19 Comparison of power(with abrupt faults)

表3是对突变故障仿真图17–19中数据的进一步分析处理.由表3可以得知所提AFSMFTC控制策略风力机运行波动更小,能直观的展现所提算法优越的容错能力.

表3 突变故障控制性能对比Table 3 Control performance comparison with abrupt faults

5.5 结论

本文针对风力机存在执行机构故障下风轮转速控制,提出了一种基于风速估计的自适应状态反馈滑模控制器.该控制器采用由积分滑模和自适应增益组成的自适应状态反馈滑模控制策略,利用状态反馈和全阶补偿器对积分滑模控制律进行设计.并分别基于LMI和Lyapunov稳定性实现了控制律参数调整和闭环系统的稳定性证明.所设计的基于VGWO算法的CRBFNN可以提高控制系统的可靠性和风速测量精度.结果表明,在健康/故障的执行机构条件下,所提容错控制方法均能获得较好的控制效果.从实际应用的角度来看,所提容错控制策略具有较小的波动和较弱的抖振,在齿轮箱和发电机等部件上显示出较少的疲劳,这对于提高风力机的寿命具有重要意义.本文所提控制策略未考虑模型不确定性对控制效果的影响,这对于验证所提容错控制算法的鲁棒性是不利的,且未来可以进一步考虑风力机相关的状态约束[30]和故障诊断问题[31].