单相电力电子变压器整流级新型直接功率控制策略

宋平岗 ,连加巍 ,陈 怡

(华东交通大学电气与自动化工程学院,江西南昌 330013)

1 引言

近年来,电力电子变压器(power electronics transformer,PET)作为一种将电力电子技术与高频变压技术结合的新型电能转换装置备受关注[1–3].在具备传统电力变压器的功能外还具有功率因数可控、谐波治理、无功补偿、能量双向流动等诸多优势[4].目前,电力电子变压器已应用于分布式新能源发电[5]、柔性交直流配电网[6]以及电力牵引[7–8]等诸多领域.因此,研究电力电子变压器具有重要意义.

目前,三级式PET较为成熟的拓扑结构有级联H桥型PET(cascaded H-bridge type PET,CHB-PET)[9]和模块化多电平型PET(modular multilevel converter type PET,MMC-PET)[10].其中,CHB型拓扑具有模块化程度高、扩展性好、易实现冗余设计等优点[4,23],是PET常用的结构.

CHBR型整流器作为电力电子变压器的前级系统,其工作性能关系到PET后级系统的安全稳定运行.其工作目标是保证电压电流单位功率因数运行以及直流侧电容电压的平衡控制.对于CHBR整流器,众多学者进行了相应的研究,各种控制策略相继被提出,大致可以分为两类:直接电流控制和直接功率控制[11].其中,直接电流控制又包括瞬态电流控制[12]、比例谐振(proportional resonant,PR)控制[13]、模型预测电流控制[14]、滞环电流控制[15]以及dq电流解耦双闭环控制[16]等控制方法.瞬态电流控制由于采用了比例P控制器,电流存在一定的稳态误差;比例谐振控制虽然能够很好的消除稳态误差,但控制性能受网侧电压频率影响较大;模型预测电流控制作为一种非线性控制策略,适用于多变量系统,但容易受外部干扰和模型失配的影响;滞环电流控制中开关频率不固定,从而易导致输出电流波形脉动较大.此外,在电力系统中网侧电压频率存在±0.5 Hz的偏移,电感参数易发生变化,这些问题都会影响系统的动态响应能力.

为应对系统网侧频率偏移和电感参数变化的影响,文献[17]提出一种无锁相环控制策略应用于柔性直流输电系统,具有功率波动小、谐波抑制能力强的特点;文献[18]设计了一种无电感参数和系统角频率的控制策略来治理铁路牵引供电系统中负序、无功以及谐波问题.然而.在电力电子变压器领域中,却鲜有文献提出相关控制策略应对系统频率偏移和电感参数变化的影响.

综上所述,为应对系统网侧频率偏移和电感参数变化的影响,本文以三级联H桥整流器为研究对象,建立电压与功率的数学模型.首先,采用级联延时信号消除模块(cascaded delayed signal cancellation,CDSC)[19–22]提取基波正序分量,消除谐波信号干扰;然后在αβ两相静止坐标系下设计了一种无需系统角频率和电感参数的新型直接功率控制器,将双环控制简化为单环控制.最后通过搭建三级联H桥整流器仿真模型进行仿真分析,并与传统dq电流解耦双闭环控制器进行对比,仿真结果验证了所提方法理论的正确性和有效性.

2 基波正序分量的提取

2.1 单相谐波信号的反共轭分解

以电压信号为例,非标准正弦波信号可以表示为基波和谐波信号之和的形式,如式(1)所示:

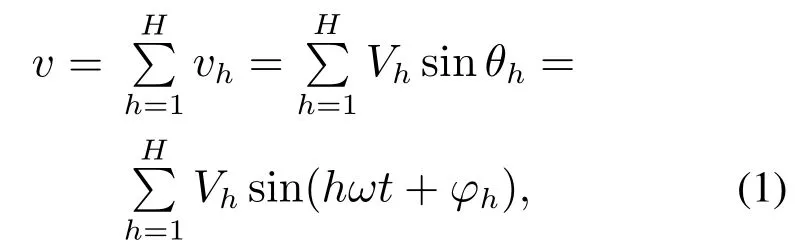
其中:Vh为电压信号的幅值;h为谐波次数;θh为相角;φh为初始相位.

在αβ静止坐标系中存在一对关于虚轴对称的空间矢量,称其为反共轭矢量[22].如式(2)所示:

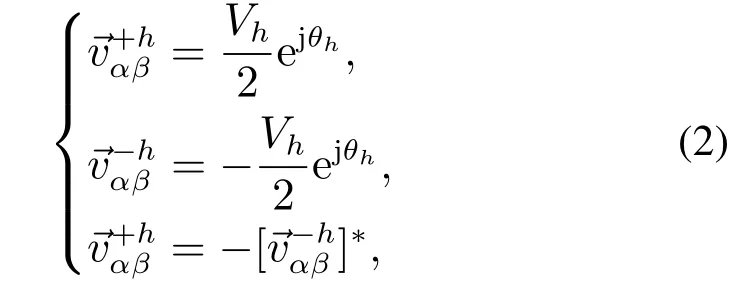
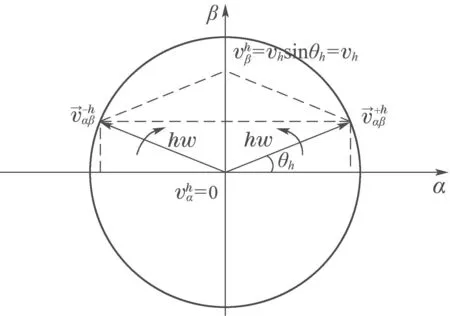
图1 反共轭分解原理图Fig.1 Schematic diagram of anti conjugate decomposition

通过式(1)和式(2)推导出两个反共轭矢量的矢量和为

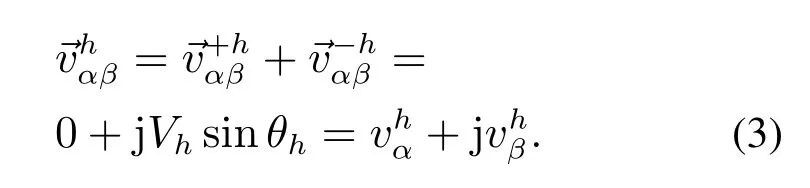
由式(3)可知任意的单相谐波信号和一个零矢量可以组成一个新的矢量,该新矢量可以被分解为一组反共轭矢量.同样,含有多次谐波的单相谐波信号与零矢量组成的新矢量集合可以被分解为反共轭谐波矢量集合的形式.通过一定的方法消除除基波正序分量以外的其他信号,就可以得到一个相对比较“干净”的基波信号.

2.2 级联延时信号消除法

根据第2.1节可知某一单相电压谐波信号可以表述为如下空间矢量的形式:

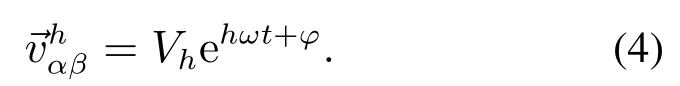
在αβ静止坐标系中,正序谐波电压矢量信号做逆时针旋转,负序谐波电压矢量信号做顺时针旋转.不同次数的谐波旋转的角频率不同,因此在相同的时间内,可以通过延时操作将其分离出来[20].

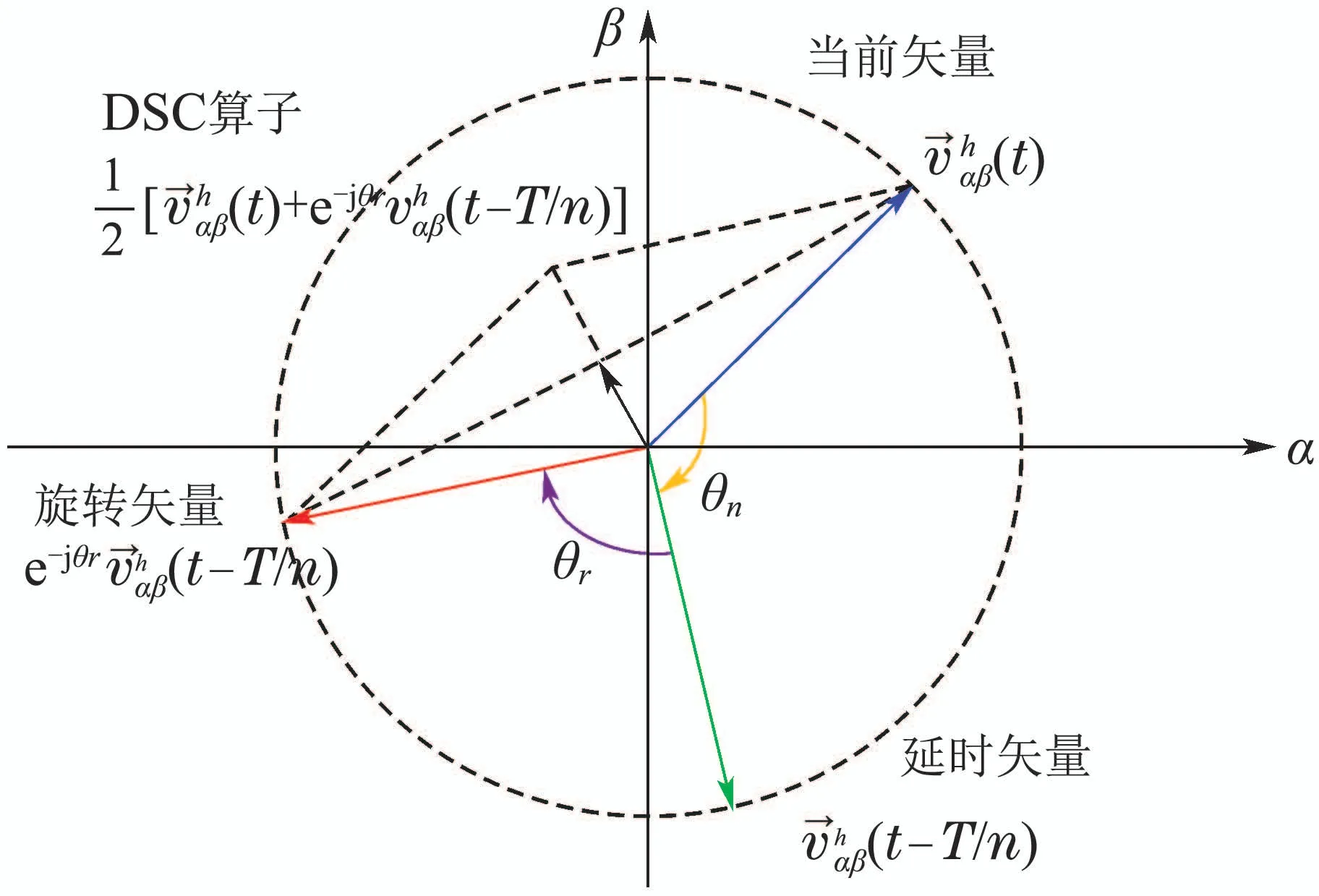
图2 延时信号消除矢量图Fig.2 Vector diagram of time delay signal elimination

应用当前矢量和旋转矢量可以构造出延时信号消除(DSC)模块,其表达式为

式(5)的时域信号表达形式为

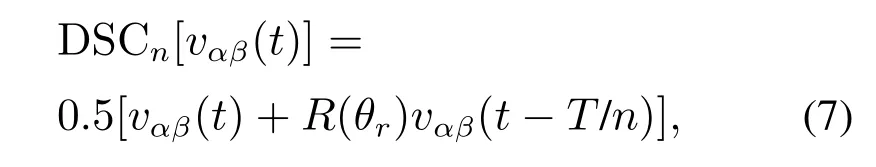
其中旋转矩阵R(θr)为

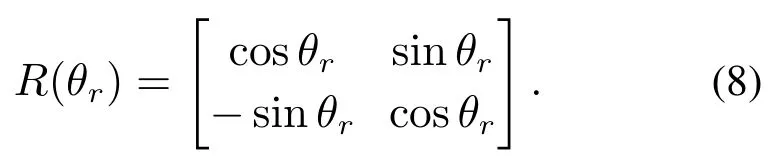
旋转角度θr为

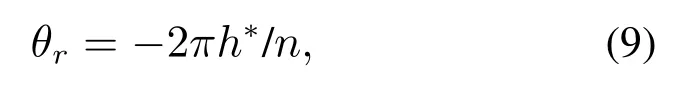
式中:h∗表示目标谐波次数,根据文献[20]的描述,当谐波次数h=h∗,即θr+θn=0时,DSC模块具有单位增益和零相移;当谐波次数h=h∗−(k+1/2)n,(k=0,±1,±2,···),即θr+θn=π时,DSC模块具有零增益.此时,这些次数的谐波将被DSC模块消除,所有单位增益和零增益点之间的谐波被衰减.单个延时信号消除模块时域结构图如图3所示.

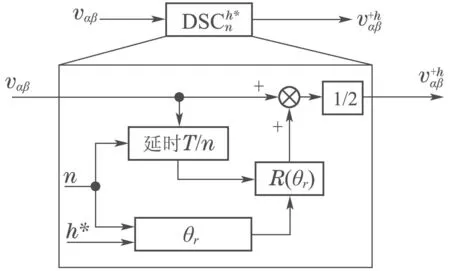
图3 单个延时信号消除模块框图Fig.3 Block diagram of a single delayed signal elimination module

由于单一的DSC模块并不能提取目标次谐波,因此可以通过构建级联形式的CDSC模块提取目标谐波,如图4所示.通过给每个DSC模块设置不同的参数就可以消除不需要的谐波,提取目标谐波信号.文献[23]指出存在多对延时因子n和目标谐波次数h∗满足消除给定谐波h的需求,且每个延时模块DSC具有多个零增益点.因此通过恰当的选取DSC模块参数就可以使得基本模块的数量远小于要消除谐波的数量,减小系统的延时时间,提高实时性.图5为选取参数h∗为1,n=2,4,8,16,325个基本单元时的DSC的幅值相应.

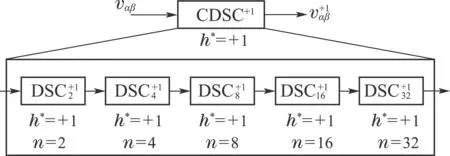
图4 基波正序分量提取CDSC结构图Fig.4 Fundamental positive sequence component extracting structural view CDSC

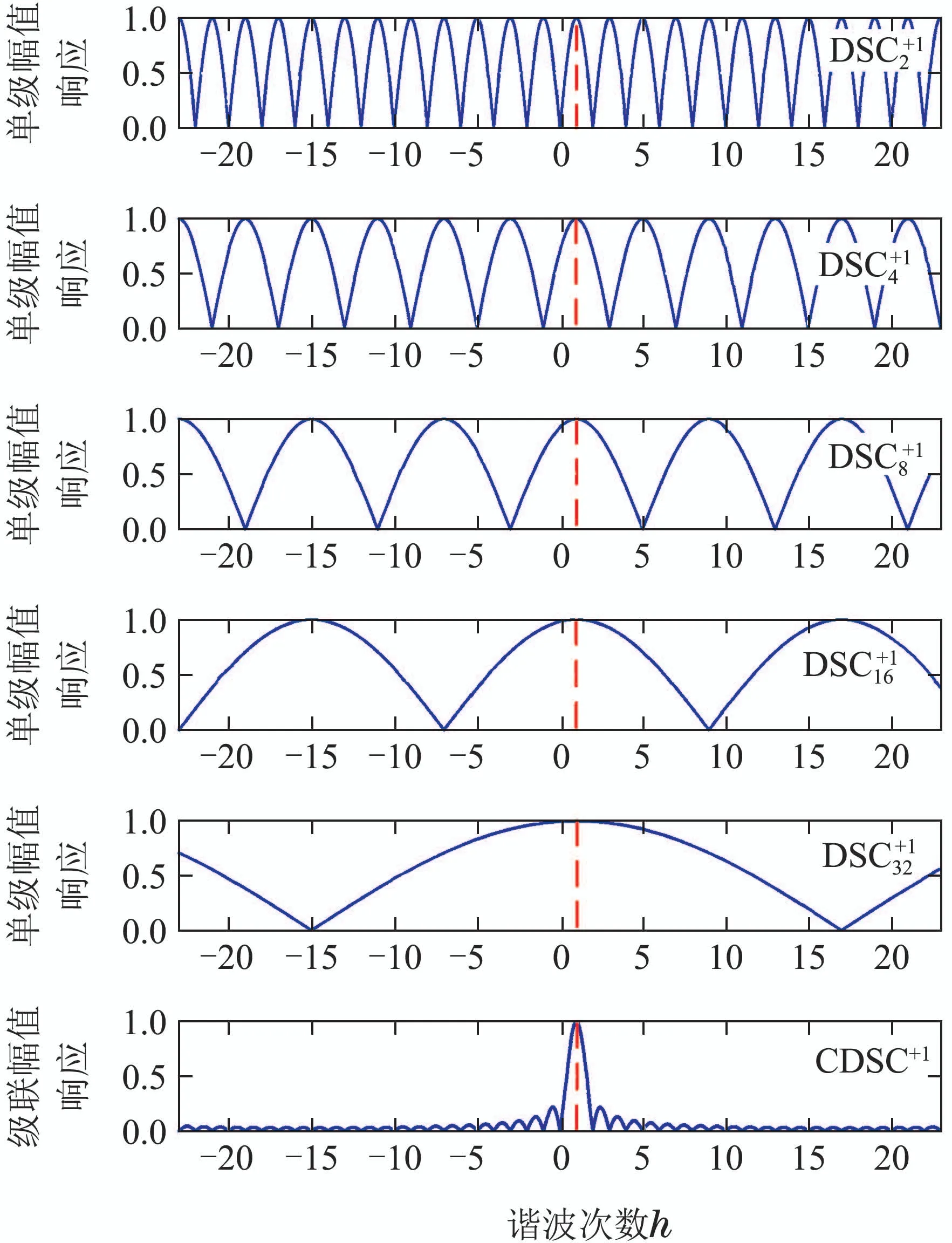
图5 CDSC算法单级和整体谐波幅值响应Fig.5 CDSC single and integral algorithm corresponding harmonic amplitude

从图5中可知直观的得出:单级DSC算子的谐波在h=1处具有统一的单位增益,在不放大某些频率分量的同时可以消除某些特定的频率分量.因此通过对多个DSC算子级联形成CDSC可以消除多种频率分量.从图5中的底图可以看出五级联的CDSC对基频正序分量的放大倍数为1,在整数倍频点幅值响应为0,非整数倍频点呈衰减特性.CDSC2,4,8,16,32在保留基频分量的同时可以很好的消除20次谐波内的高次谐波分量.

通过进一步的分析表明,虽然CDSC2,4,8,16,32具有良好的谐波消除能力,但是其总体延时时间为0.97个周期,并未有良好的优势.考虑到单相电力电子变压器整流级主要以奇次谐波为主,因此文章选择CDSC4,8,16,32作为级联延时模块进行基波正序分量的提取.

图6为CDSC2,4,8,16,32和CDSC4,8,16,32的幅值响应对比图.从图中可以看出在同一范围内CDSC4,8,16,32所有的奇数阶均为零增益,尽管偶次阶不为零,但考虑到单相系统中偶次谐波的幅值相对于奇次谐波幅值小得多,因此通过CDSC4,8,16,32可以将偶次谐波衰减到可以忽略的程度.其总体延时时间为0.44个周期,系统的实时性得到大幅提升.

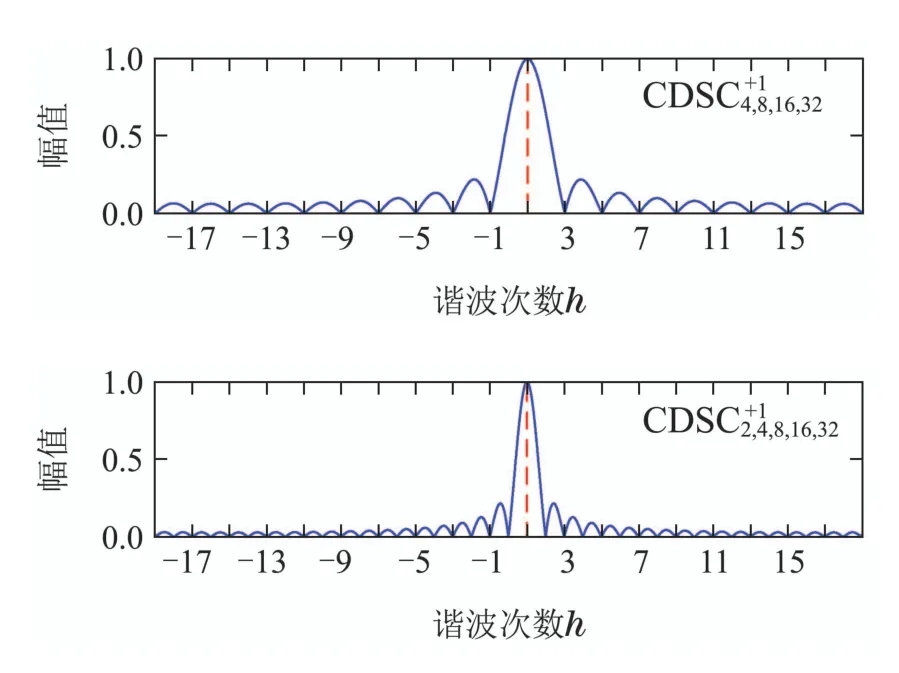
图6 两种级联延时算法幅值响应对比图Fig.6 Comparison of amplitude response of two cascaded delay algorithms

3 整流级直接功率控制策略

3.1 单相级联H桥整流器数学模型

单相电力电子变压器整流级为级联H桥整流器,其三级联拓扑结构如图7所示.图中us,is为网侧电压、电流;R0,L0为网侧等效电感和等效电阻;uab为交流侧输入电压.其中Si1,Si2,Si3,Si4(i=1,2,3)为第i个H桥的开关器件.C1,C2,C3为直流侧等效电容,uC1,uC2,uC3为各级H桥单元直流侧电压;R1,R2,R3为各H桥直流侧等效负载.

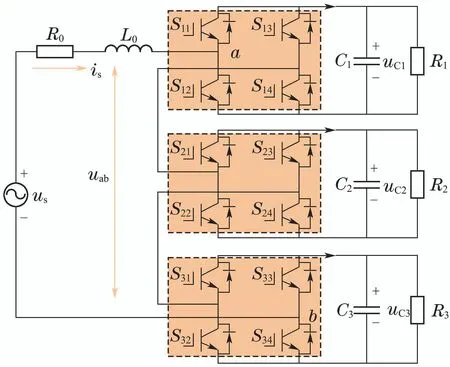
图7 三级联CHBR拓扑结构图Fig.7 Topological structure diagram of three-cascade CHBR

假设系统处于理想工作状态.由于各级联单元之间互相等效,功率均衡分布.因此,为简化分析,将CHBR等效为一个单相全桥结构的PWM整流器进行数学模型分析.其等效拓扑结构图如图8所示.

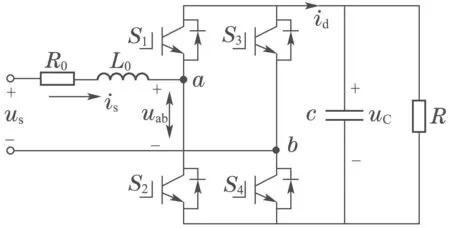
图8 单相PWM整流器拓扑结构图Fig.8 Topological structure diagram of single-phase PWM rectifier

根据KCL定律可得交流侧、直流侧数学方程为

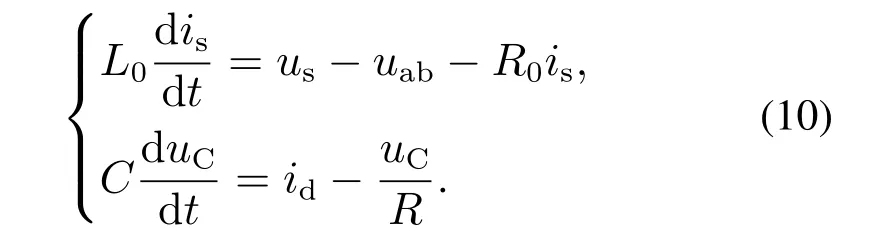
3.2 单相级联H桥整流器直接功率控制原理

为便于分析,令网侧电压αβ轴的分量为

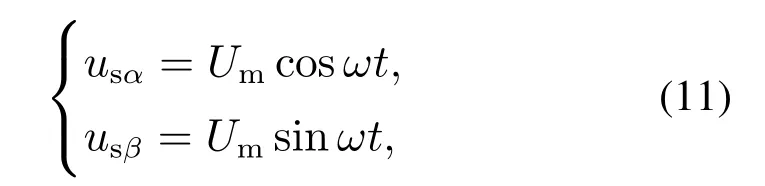
其中:Um为网侧电压幅值;ω为工频频率.

通过前述章节的CDSC模块进行基波正序分量提取并由式(10)得到αβ坐标系下的交流侧电压方程为

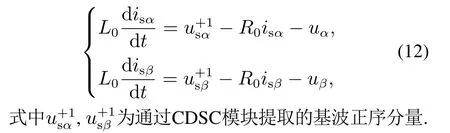
单相系统在αβ坐标系下的有功功率和无功功率表达式可以表示为

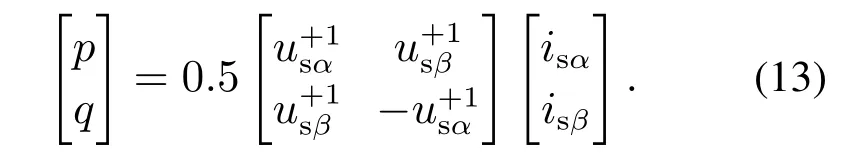
对功率进行求导可得

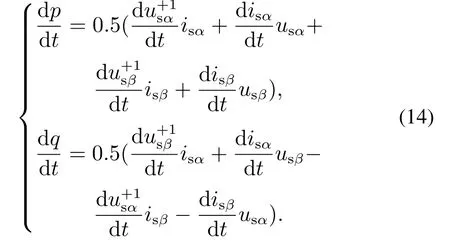
将式(11)经过求导联立式(12)和式(14)经过化简可得

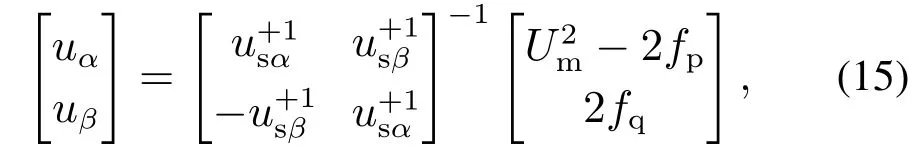
其中fp和fq的表达式为

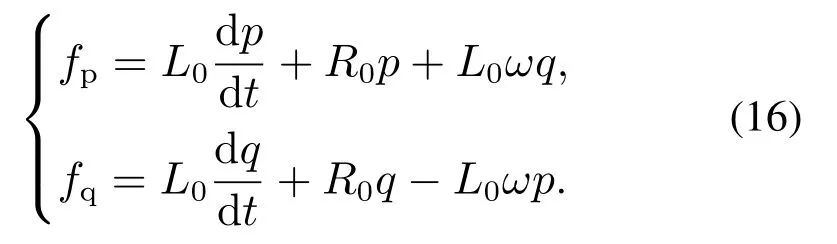
3.3 新型直接功率控制器设计

由式(15)和式(16)可知系统的有功功率和无功功率存在耦合,为了实现对有功和无功的独立控制需要设计相应的控制器对功率进行解耦.由于级联H桥整流器在实际的运行中等效电感参数可能会受到各种因素干扰,并且考虑到网侧电压频率存在±0.5 Hz的偏移.因此文章提出一种无需电感参数和系统角频率的功率解耦控制器,该控制器的设计需要借助合成矢量[24]来设计,令Mpq=p+jq.则

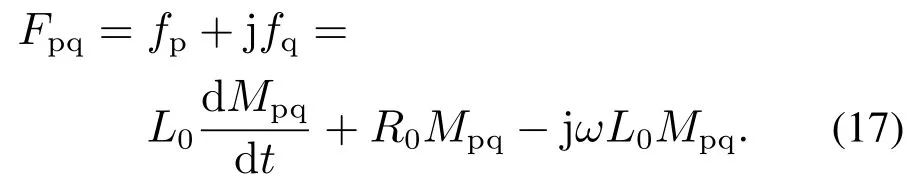
将式(17)转化为s域形式,经过化简后可得

求解式(20)可得

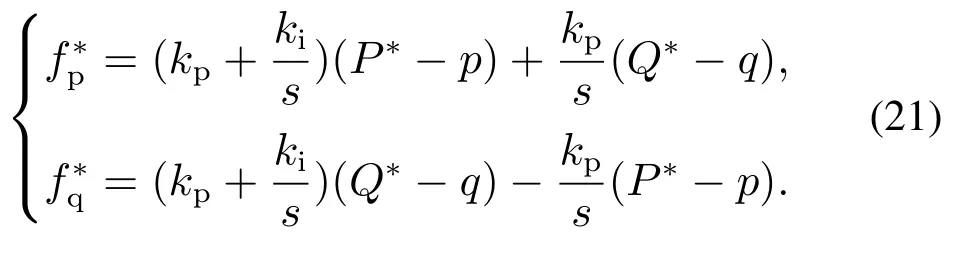
无电感参数和系统角频率的功率解耦控制框图如图9上部框图所示,通过式(15)进而可以得到电压前馈控制的模型为

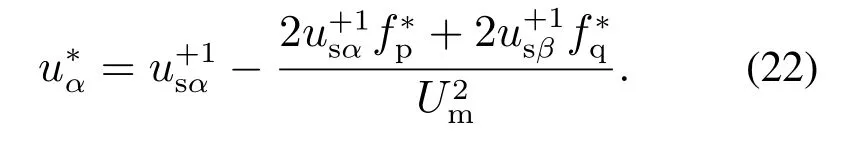
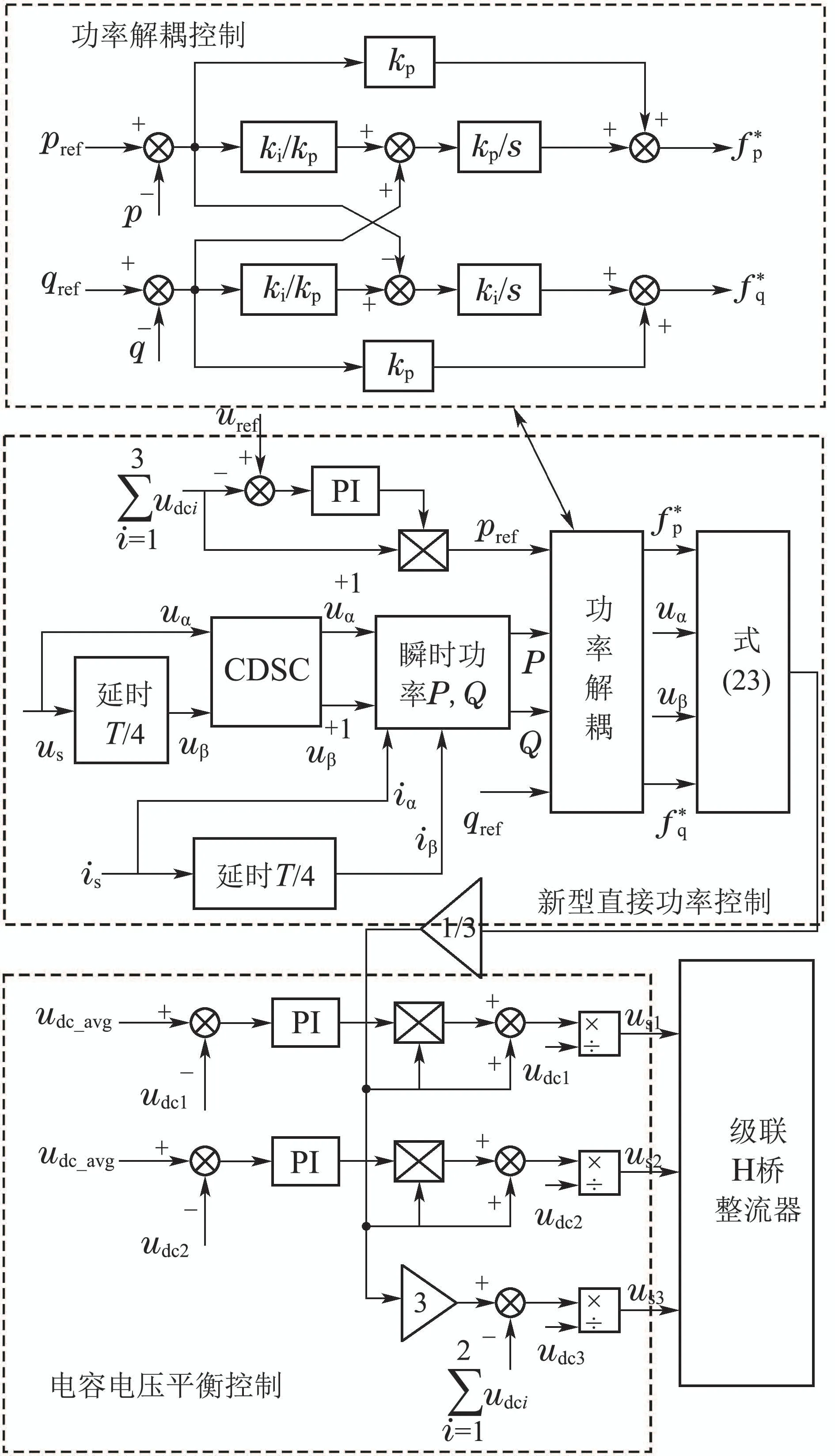
图9 级联H桥整流器控制框图Fig.9 Control block diagram of cascaded H-bridge rectifier

注1因β轴上的分量是通过CDSC模块得到的虚拟正交分量,不具有实际的物理意义,因此式(22)仅给出了α轴分量的表达式.

3.4 单相级联H桥整流器电容电压平衡控制

单相级联H桥整流器作为电力电子变压器的前级系统,各H桥输出电压的平衡关系到后级DC-DC变换器的功率均衡控制以及逆变器的平稳运行.因此,级联H桥整流器的控制包括整体控制和各H桥直流侧电容电压的平衡控制.本文在直接功率整体控制的基础上采用一种基于平均电压法的电压平衡控制方法[25]来实现对各H桥的电容电压平衡控制,控制框图如图9下部框图所示.

至此,级联H桥整流器的整个控制过程为:1)通过直接功率控制方法获得H桥整流器的PWM调制信号2)在电容电压平衡控制中,输出电压总和的平均值udc-avg与各级联模块输出电压之差通过PI控制器输出后与平均电压参考值的乘积,加上平均电压参考值然后与各H桥电容电压输出值相除得到前两个H桥单元的调制波信号us1和us2;总的电压参考值减去前两个H桥单元电压输出值之和,然后和第3个H桥单元电压输出值udc3相除得到第3个H桥单元的调制波信号us3.

4 仿真分析

为了验证本文所提新型直接功率控制策略的正确性和有效性,在MATLAB/Simulink中搭建三级联H桥整流器进行验证.模型仿真参数如表1所示.

表1 三级联CHBR仿真参数Table 1 Three-cascade CHBR simulation parameters

工况1 谐波抑制能力仿真分析.

为了验证CDSC级联延时信号消除模块的谐波抑制能力,在网侧电压中注入幅值为基波电压幅值40%的3次谐波、20%的5次谐波、10%的7次谐波、5%的9次谐波.在文章所提直接功率控制策略的基础上采用CDSC模块和采用传统SOGI[18]模块构造的αβ分量进行对比分析.仿真结果如图10所示.为便于对比分析,电流值缩小0.5倍显示于图中.

从图10(a)可以看出,文章所提新型直接功率控制策略下,网侧电压电流保持同相位,实现了单位功率因数运行.图10(b)和10(c)可以得知,当网侧电压发生畸变时,CDSC算法使得电流输出波形保持良好的正弦性,而采用SOGI时电流产生了畸变.

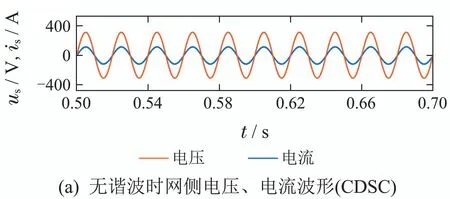
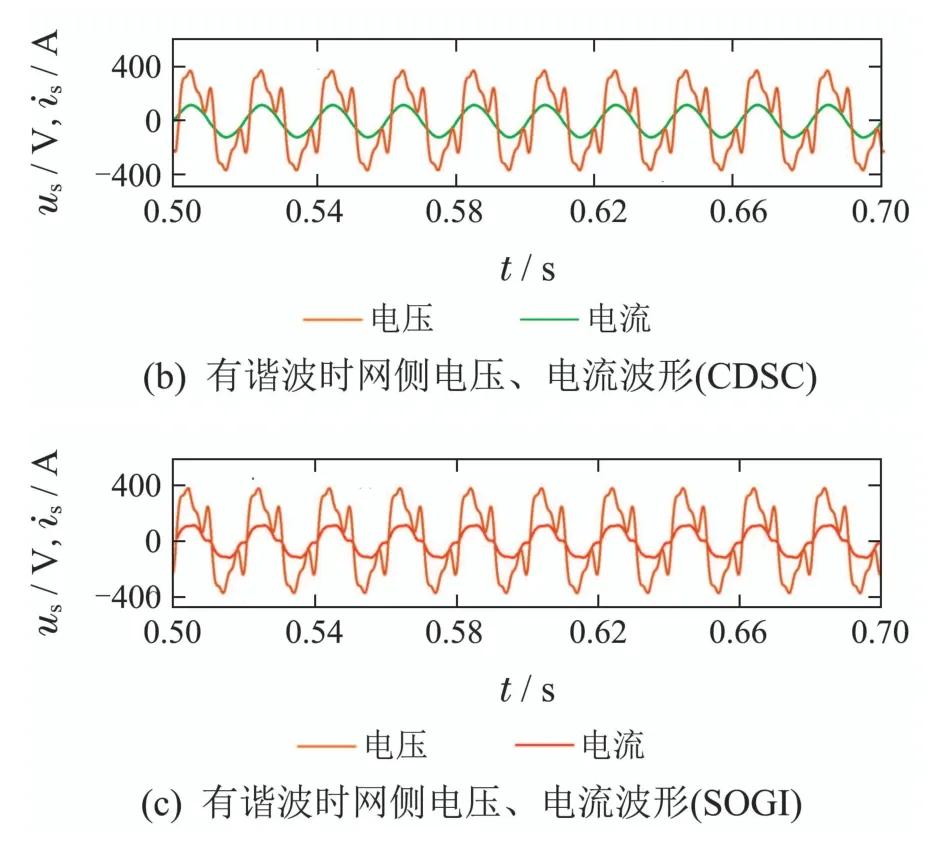
图10 网侧电压、电流波形图Fig.10 Grid-side voltage and current waveforms

图11和表2为两种算法下网侧电流的频谱分析图和各次谐波含量图.经过对比可知,采用CDSC算法时电流的THD值更低,谐波抑制能力更强.

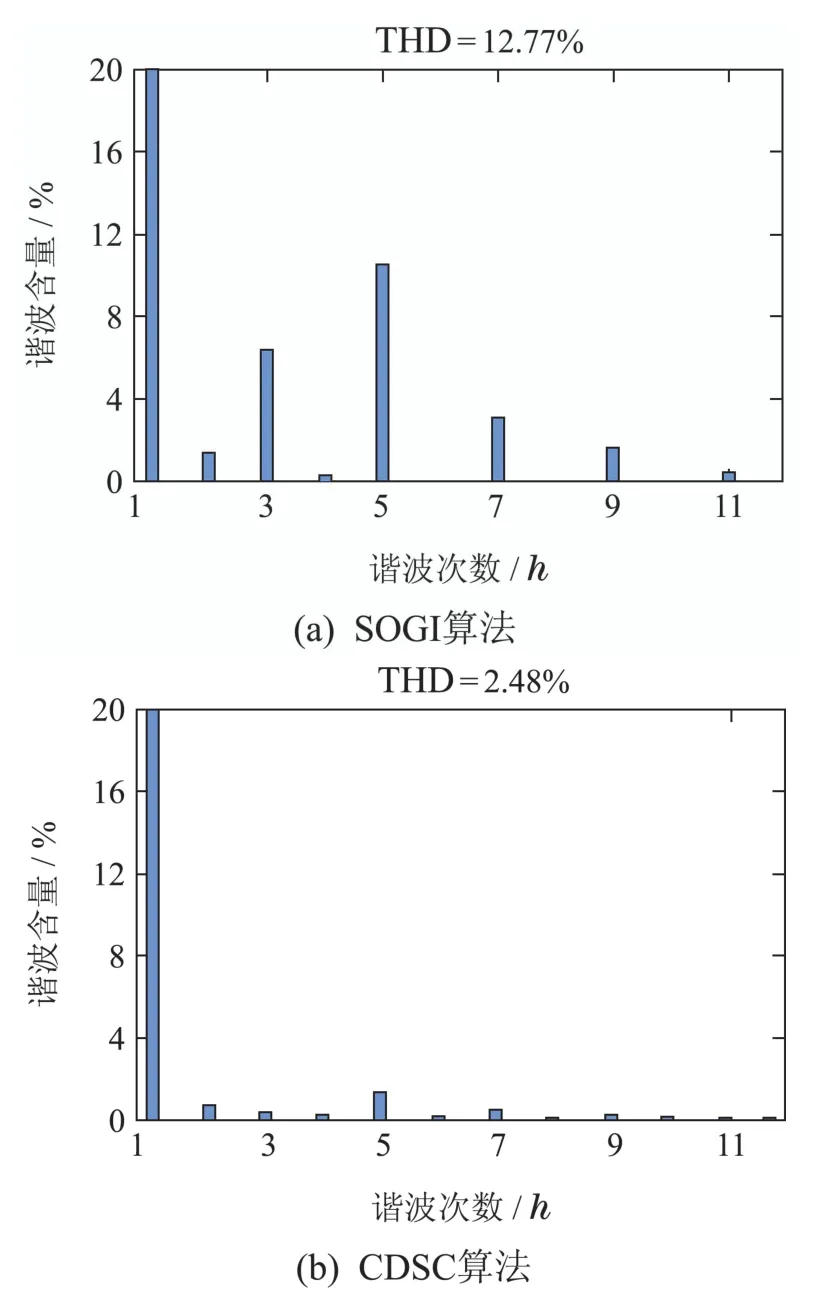
图11 网侧电流is频谱分析图Fig.11 Grid-side current is spectrum analysis diagram

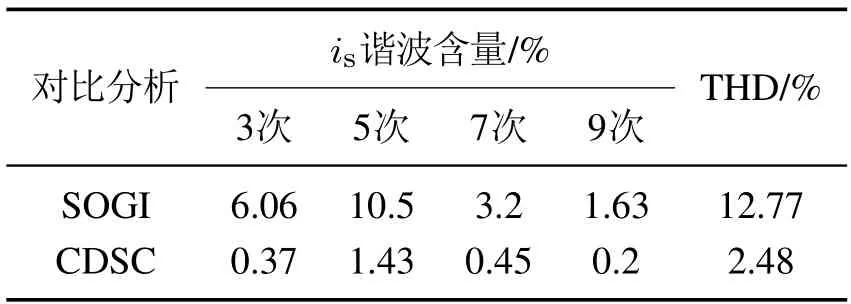
表2 网侧电流谐波含量及THD值分析Table 2 Grid-side current harmonic content and THD value

工况2 直流侧负载不平衡及突变时仿真分析.

在负载不平衡和负载突变的情况下验证所提新型直接功率控制策略的应对能力.取R1=100 Ω,R2=120 Ω,R3=140 Ω时验证负载不平衡时控制效果.在负载相同情况下,t=1.0 s时负载突变为R1=120 Ω,R2=140 Ω,R3=160 Ω时验证负载突变时的控制效果.仿真结果如图12所示.

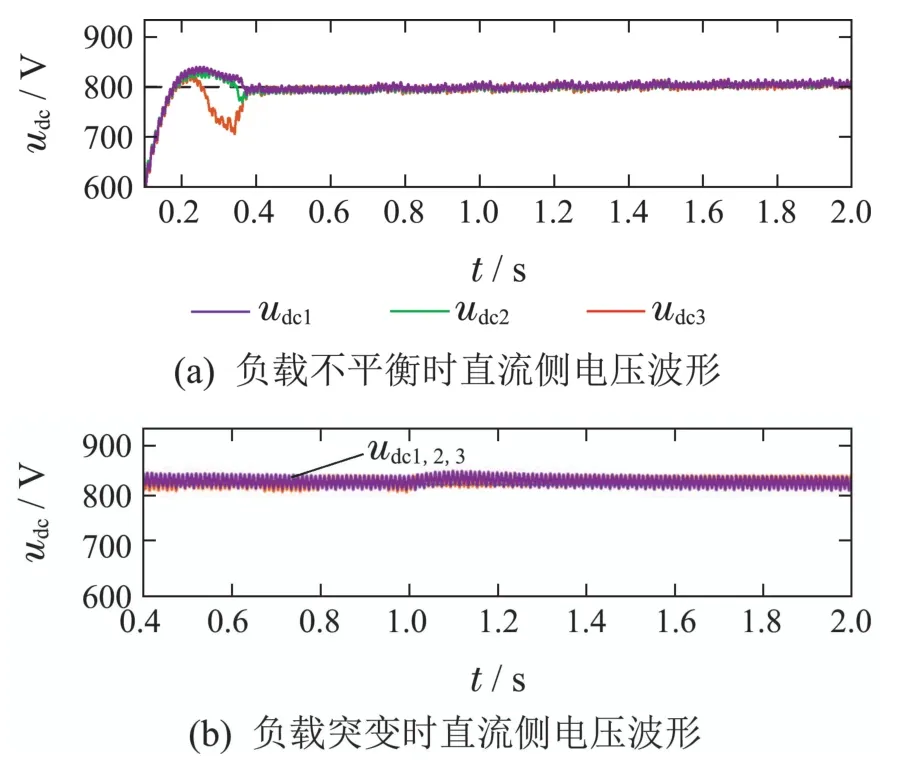
图12 直流侧负载不平衡以及突变状态下波形图Fig.12 Waveform diagram of DC side load imbalance and sudden change state

由图12可知文章所采用控制策略能够实现直流侧电压在负载不平衡以及负载突变条件下平衡稳定输出.

工况3 网侧电压频率偏移仿真对比分析.

为了验证所提控制策略能否良好应对网侧电压频率偏移的影响,仿真频率初始值设为49.5 Hz,在0.4 s至0.6 s期间,频率f以2.5 Hz/s的速度偏移至50.5 Hz,0.6 s后维持50.5 Hz不变.并与传统dq电流解耦控制做对比,仿真结果如图13–14所示.

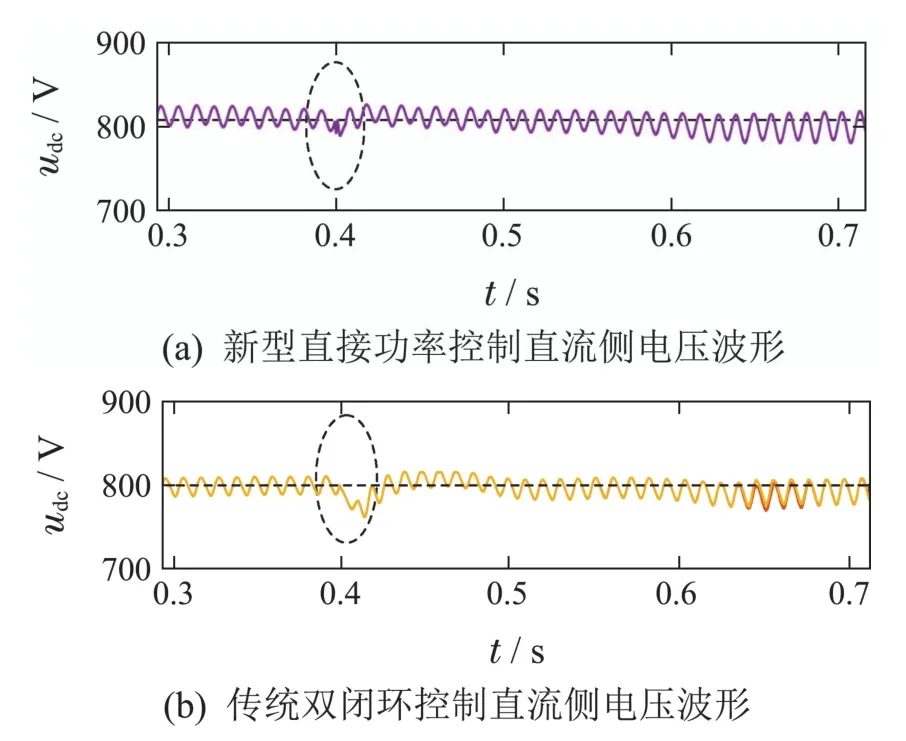
图13 频率偏移时直流侧电压波形图Fig.13 Waveform of DC side voltage in case of frequency offset

图14为图13中椭圆虚线部分放大波形图,从图中可以看出,当频率发生偏移时,传统dq电流双闭环控制下直流侧电压波形波动明显,上下幅值波动达到50 V,而文章所提新型直接功率控制策略下直流侧电压波形波动较小,上下幅值波动为36 V,仿真验证了新型直接功率控制策略能够很好应对频率偏移的影响.

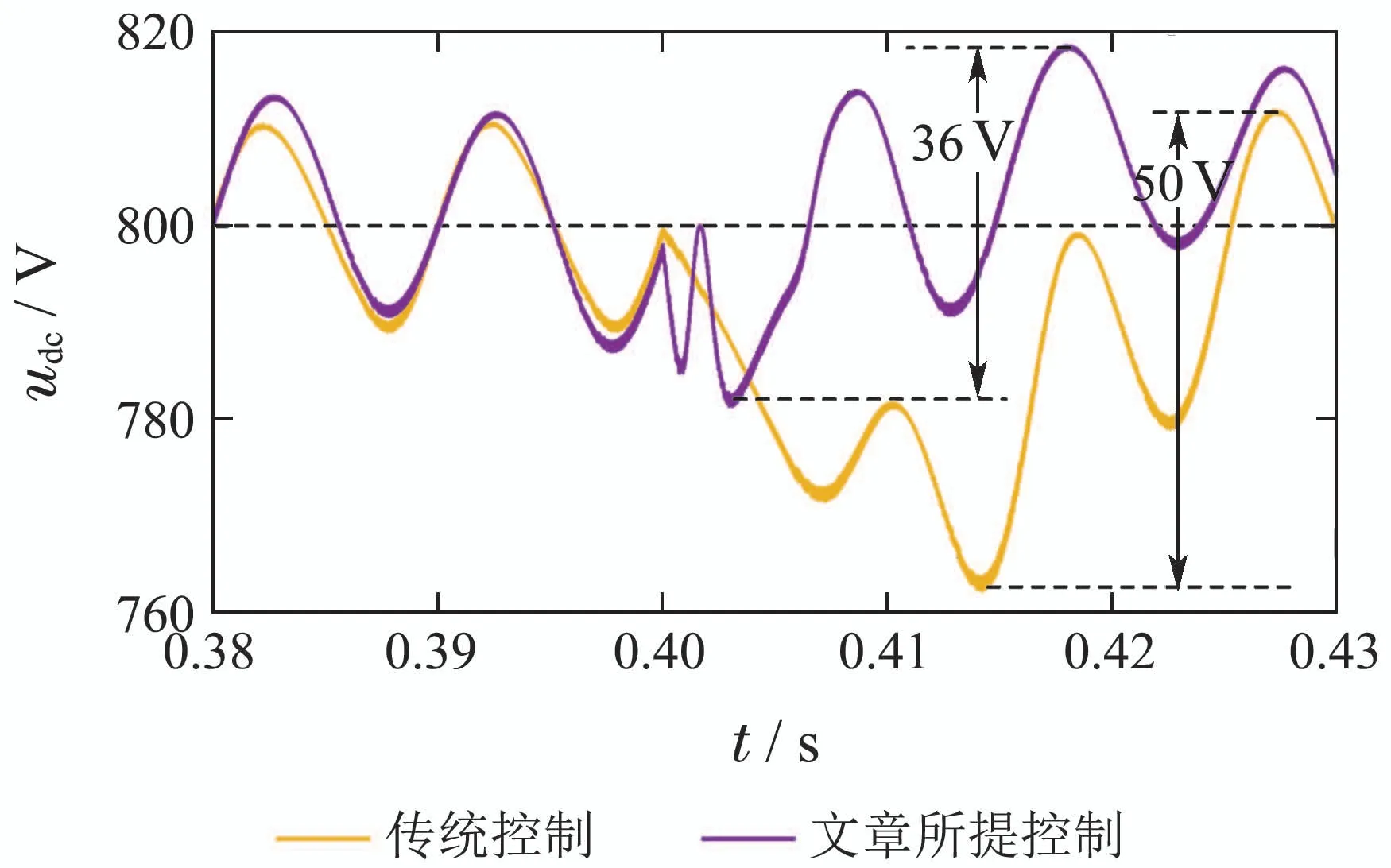
图14 直流侧电压放大波形对比图Fig.14 Comparison diagram of DC side voltage amplification waveform

工况4 网侧电压相位突变仿真对比分析.

为了验证所提控制策略能否良好应对网侧电压相位突变的影响,在t=0.7 s时,相位由0◦突变为120◦;并与传统dq电流解耦控制做对比,仿真结果如图15和图16所示.

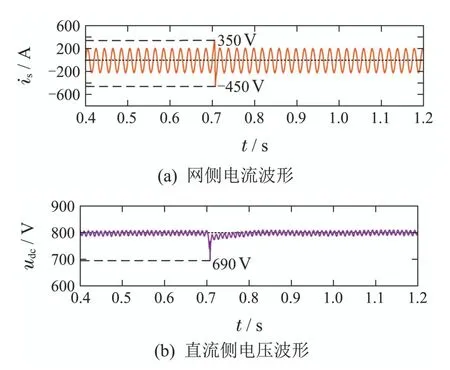
图15 新型直接功率控制电流、电压波形图Fig.15 The current and voltage waveforms of the new direct power control

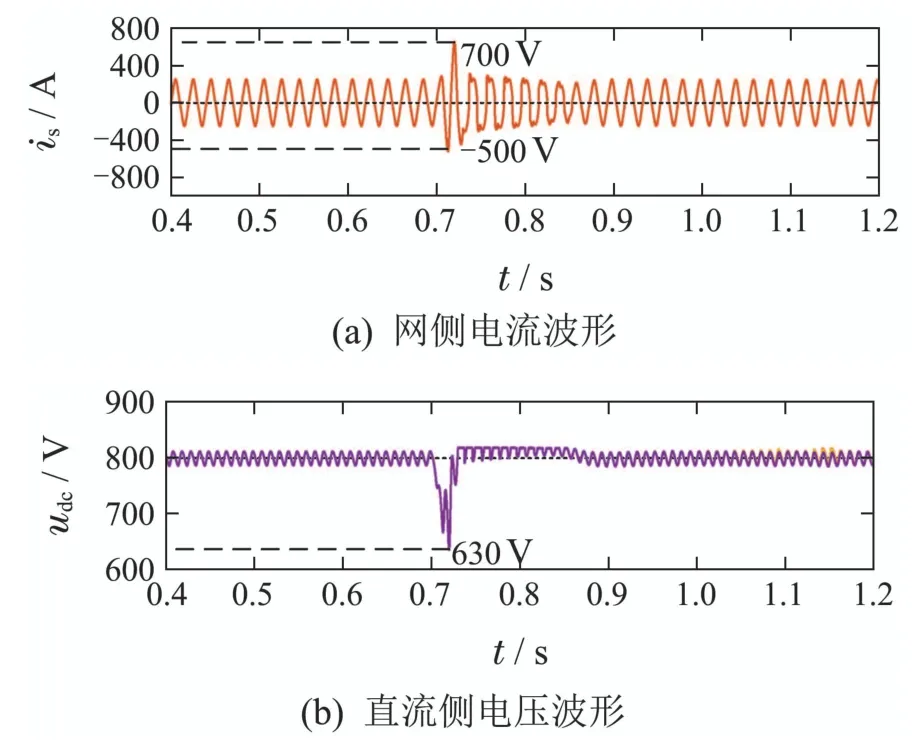
图16 传统双闭环控制电流、电压波形图Fig.16 Traditional double closed-loop control current and voltage waveforms

从图中可知,0.7 s时相位发生突变时,新型直接功率控制策略下,网侧冲击电流范围为−450 A至350 A,直流侧电压波形最低跌至690 V,0.8 s左右迅速恢复电压给定值.而采用传统双闭环控制下,网侧冲击电流范围为−500 A至700 A,直流侧电压波形最低跌至630 V,0.9 s时恢复至系统给定值.并且从图中可以明显看出,传统双闭环控制下,网侧电流和直流侧电压在恢复的过程中波形出现明显的畸变.仿真结果验证了新型直接功率策略能够很好应对相位突变的影响.

工况5 交流侧等效电感突变仿真对比分析.

为了验证所提控制策略能否良好应对交流侧等效电感变化的影响,在t=0.6 s时,在L0=5 mH的基础上并联一个1 mH的电感.并与传统dq电流解耦控制做对比,仿真结果如图17和图18所示.

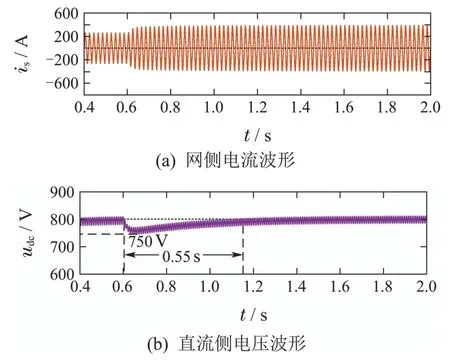
图17 新型直接功率控制电流、电压波形图Fig.17 The current and voltage waveforms of the new direct power control

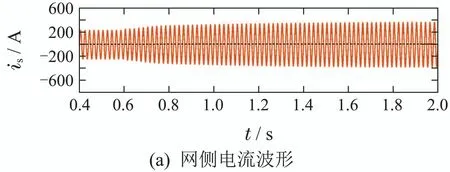
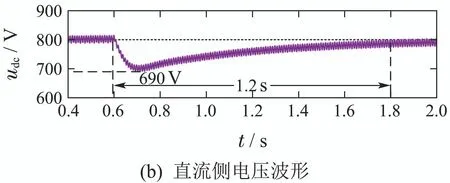
图18 传统双闭环控制电流、电压波形图Fig.18 Traditional double closed-loop control current and voltage waveforms

从图中可知,文章所提的新型直接功率控制方法下,直流侧电压最大跌幅跌落至750 V,且能够在0.55 s左右迅速恢复至稳定状态.而采用dq电流解耦双闭环控制时,由于受电感参数影响,直流侧电压最大跌幅跌落至690 V,恢复至稳定状态需要1.2 s.仿真结果验证了新型控制策略能够很好应对系统电感参数变化的影响.

5 结论

本文以三级联H桥整流器为研究对象,提出了一种采用CDSC算法提取基波正序分量,且无需电感参数和系统角频率的新型直接功率控制器,得出以下结论:

1) 新型直接功率控制器将传统的双环控制简化为单环控制,控制器设计简单,实现了有功、无功功率的独立解耦控制.

2) 新型直接功率控制器能够快速应对频率偏移、初始相位角变化以及电感参数变化的影响,能够快速实现电压的平衡控制,动稳态特性较好.

3) 新型直接功率控制器还具有良好的谐波抑制能力.