电流频谱Hurst指数在串联电弧故障检测中的应用
江 军,李 威,李 波,马径坦,张潮海
(1.江苏省新能源发电与电能变换重点实验室(南京航空航天大学),江苏南京 211106;2.国网江苏省电力有限公司电力科学研究院,江苏南京 211103)
1 引言
电气接插件之间的接触不良或者线缆芯线损伤等故障会导致故障点处产生串接于负载和线路之间的串联电弧.由于串联电弧故障发生时线路电流幅值变化微弱、无法为普通保护电器检测,串联电弧可长期存在,其产生热量容易导致故障点处绝缘碳化、起火燃烧.2020年全国电气火灾总数约8.5万起,占已查明全部火灾数量的33.6%[1].因此串联电弧故障的检测研究,对于减少火灾的发生、保护人身安全有着重要意义.
电弧的“燃烧–熄灭”过程伴随着复杂的理化反应,可基于可听声信号[2]、可见光图像信号[3]、紫外光学信号[4]以及射频信号[5]实现故障检测.上述检测手段仅能应用于开关柜、航空器机舱等特定场合,普适性的检测手段是线路电流信号.且由于线路阻抗的存在,系统节点电压也蕴含故障信息,可单独基于节点电压[6]或者综合运用电压–电流波形[7]开展串联电弧故障检测.
串联电弧强烈的时变、非线性特性会导致电流波形的畸变.因此,首先可基于时域特征如“平肩部”长度[8]、方差[9]和高频脉冲数目[10]等特征实施故障检测.其次,波形的变化会呈现于电流频谱,故可通过快速傅里叶变换、短时傅里叶变换[11]和分数阶傅里叶变换[12]等手段提取频谱幅值、谐波含量以及光谱色散指数[13]等相应特征.然后,电弧的存在增大了系统的有功损耗,可通过能量域特征如功率谱熵[14]和小波熵[15]等予以表征.最后,可将电流波形映射至非电量空间提取特征.如波形图像中高频谐波对应的条纹特征[16]、相空间中电流波形的信息维数[17],以及通过模态分解获取的本征模函数[18]等.
不同负载的特征变化范围在故障前后存在交叉重叠,难以基于单一领域的特征量结合阈值算法实现检测.故需基于多领域特征量通过人工智能算法实现故障检测.串联电弧故障检测领域常用的人工智能算法有深度神经网络[19]、卷积神经网络[20]、支持向量机[21]、决策树[22]和自动编码器[23]等.既有方案检测准确率可达98%,但特征提取构造计算量大、检测算法流程复杂,依赖高性能数字信号处理器(digital signal processor,DSP)[25]等平台实现.因此,探索基于相对简单的故障特征、整体计算量较小的实用化检测方案是串联电弧故障检测研究的难点.
由于电弧燃烧的随机性,获取大量可信的实际燃弧波形存在困难,有必要通过数值仿真手段进行补充研究,这要求建立准确的电弧模型.磁流体模型(magnetohydrodynamics,MHD)能准确模拟电弧燃烧的微观过程,但计算复杂难以广泛应用.黑盒模型基于微分方程模拟电弧电气特性,易于实现,然而经典模型缺乏对电弧随机性和高频分量的表征.此外,由于电弧与负载之间存在耦合效应[25],精确的负载模型有利于提高电弧模型的可信度.但既有负载建模的文献报道较少,缺乏用于串联电弧故障模拟的非线性负载建模尤其是电力电子负载的建模.
为填补上述空白,本文探索了包括电力电子负载在内的非线性负载的电路建模;为Mayr模型增加了表征高频特性的弧柱电感和间隙电容,以及模拟电弧重燃的压控随机开关.为解决电弧检测方案实用化难点,本文引入Hurst指数将频域特征简化为单个指标,结合时域波形重构矩阵的奇异值和单层BP神经网络探索了一套针对包括电力电子设备在内的复杂负载类型、能运行于嵌入式平台的实用化检测方案.
2 串联电弧与负载建模
2.1 串联电弧建模
电弧发生器产生的串联电弧如图1(a)所示,可由弧柱电阻、弧柱电感和电极之间的分布电容(间隙电容)表征.基于此,本文采用如图1(b)所示的改进型Mayr模型描述串联电弧.

图1 串联电弧模型Fig.1 Series arc models
图中,RMayr,Larc和Carc分别对应弧柱电阻、弧柱电感和间隙电容,Larc经验值为2 nH,Carc实测均值为17.175 pF,RMayr由式(1)表示:
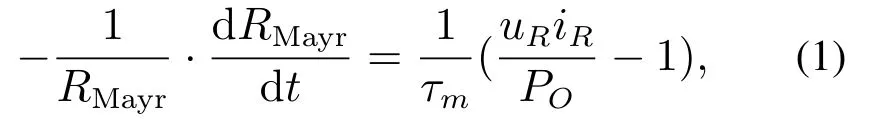
其中:τm为电弧时间常数,经验值为0.312 s;PO为电弧散热功率常数,经验值为0.1 W;uR为弧道电阻两端电压;iR为弧道电流.开关S1和S2为互锁开关,用于模拟电流过零点附近电弧的随机重燃.以S1为例,其控制律由式(2)描述:
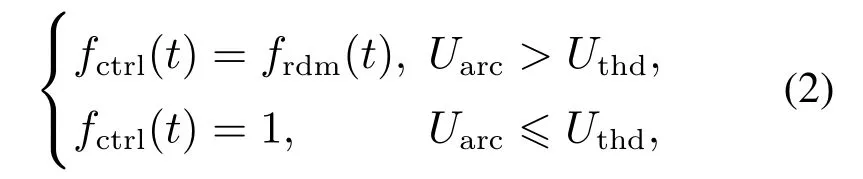
式中:fctrl(t)是开关S1的控制函数,0,1分别表示关断和开通;frdm(t)是时域上随机分布的0–1序列;Uarc是电弧模型两端的电压,Uthd是电弧重燃电压阈值,经验值为5 V.
2.2 负载建模
根据UL–1699标准,选取白炽灯作为阻性负载的代表,电风扇和吸尘器作为电机类家用负载的代表,卤素灯、荧光灯和开关电源作为电力电子类家用电器的代表开展建模研究.对于电弧产生的高频分量激励,必须考虑杂散电容的影响,故基于经验值和实物测绘结果构建了如图2所示的各类负载电路模型.

图2 6种负载的电路模型Fig.2 The circuit models of 6 kind of loads
图2(b)中的电容C2,C3和图1(c)中的电容C1均为电机绕组的等效分布电容.图2(e)中的电阻R1为灯管等效电阻(不考虑启动过程),其数值按式(3)计算[26]:

式中:RL为灯管的等值电阻;PL为灯管额定功率.
为确定模型的精确程度,考察模型与实物在有功功率和功率因素上的差异,结果如表1所示.可见误差均在10%以内,满足工程应用要求.

表1 模型仿真参数与实测值对比Table 1 Comparison of simulation and experiment result
为进一步确认模型输入电流波形的拟合度,对比仿真和实测电流波形如图3所示.可见除卤素灯模型外,其余模型仿真波形与实测波形基本一致.卤素灯仿真波形虽然与实测波形存在差异,但二者包络基本一致,仍可用于仿真试验.
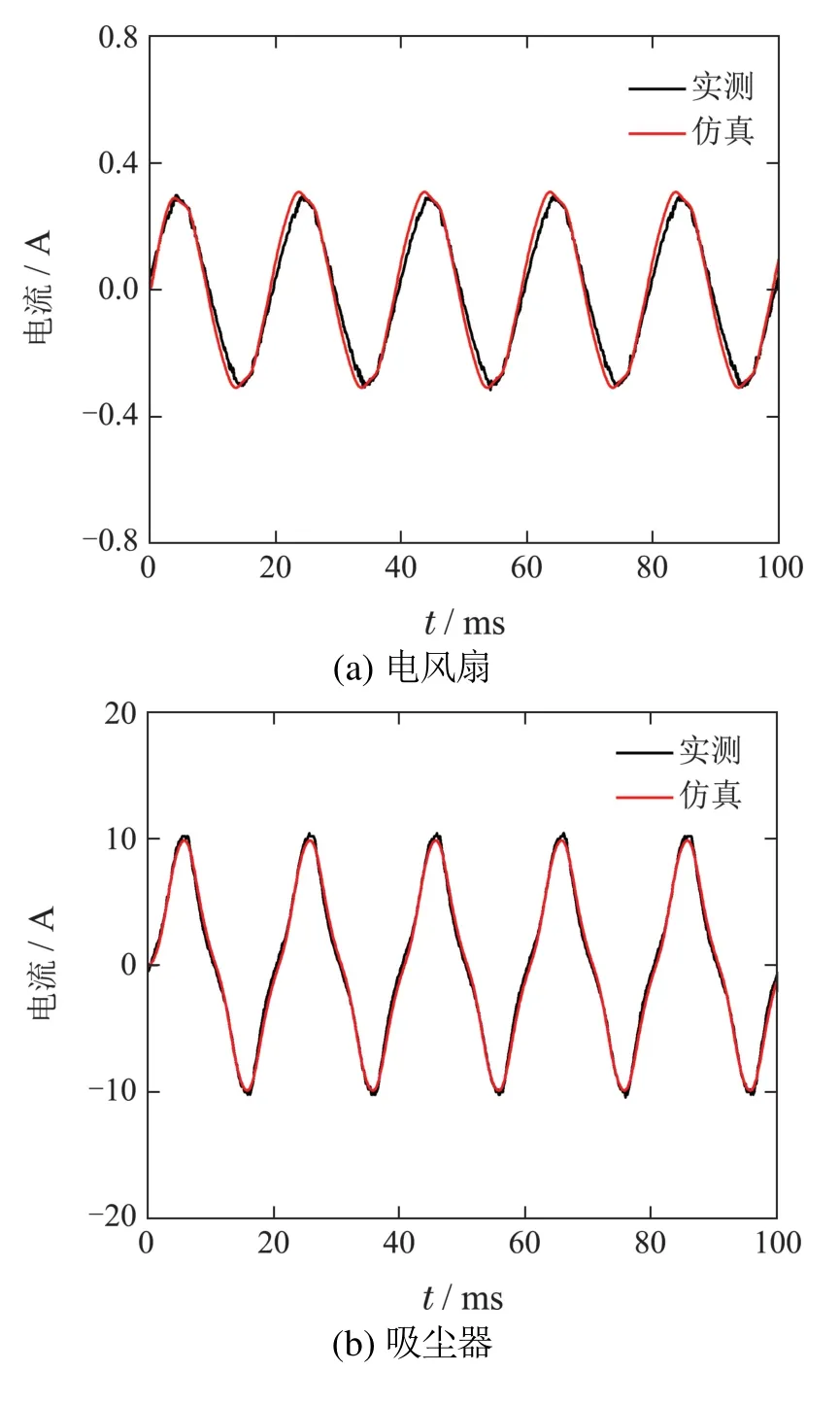
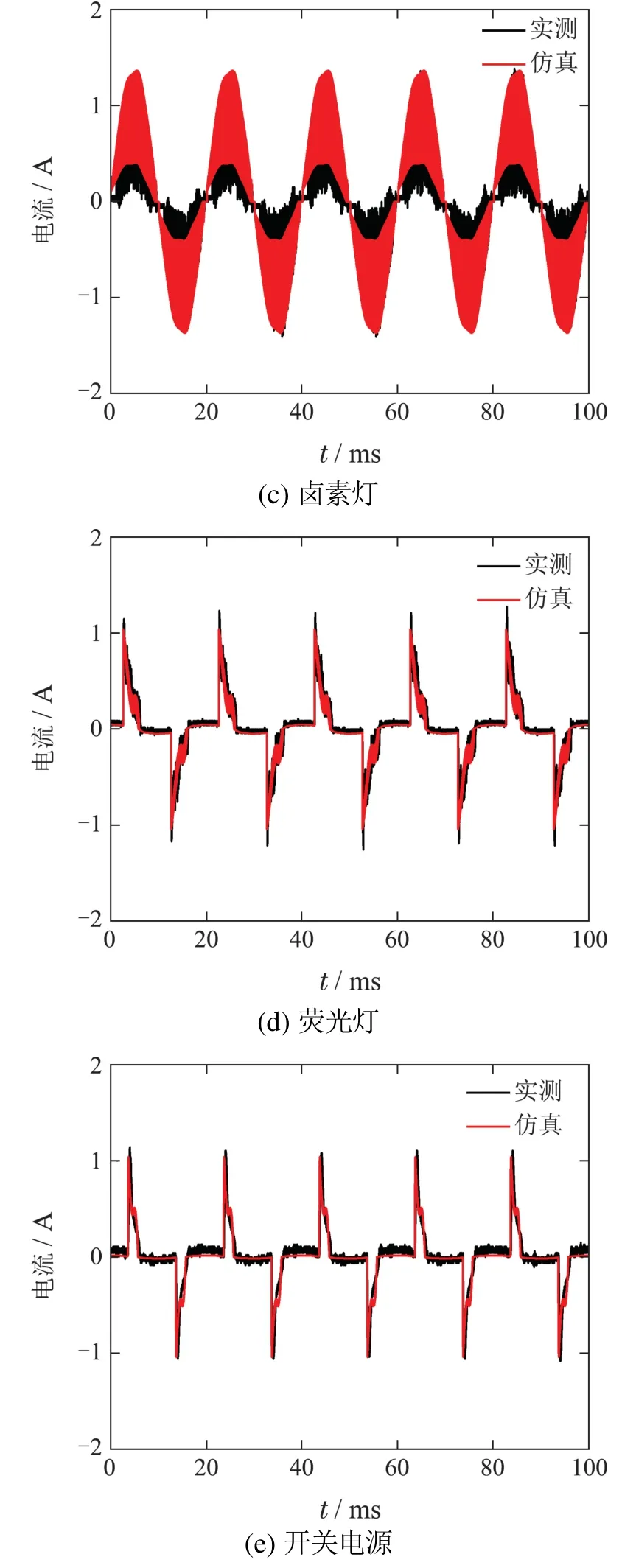
图3 负载模型输入电流仿真波形与实测波形对比(采样率1 MHz)Fig.3 Current waveforms comparison between simulation and experiment under a sample rate of 1 MHz
综上,本节建立的6种负载模型在有功功率、功率因素和输入电流波形包络与高频分量表征等3个方面具有较高的拟真度,具备实物替代性.
2.3 电弧与负载模型仿真波形分析
将改进的电弧模型与负载模型串联组合进行仿真,典型的仿真波形与实测波形对比如图4所示.仿真波形较好地反映了实测波形的平肩部、尖刺状脉冲等特征,仅在幅值上存在一定偏差.这是由于自制的测量电路其实际增益与设计值之间的偏差造成的.由此可以认定,本节中的电弧模型可信度较高,可替代试验开展研究.
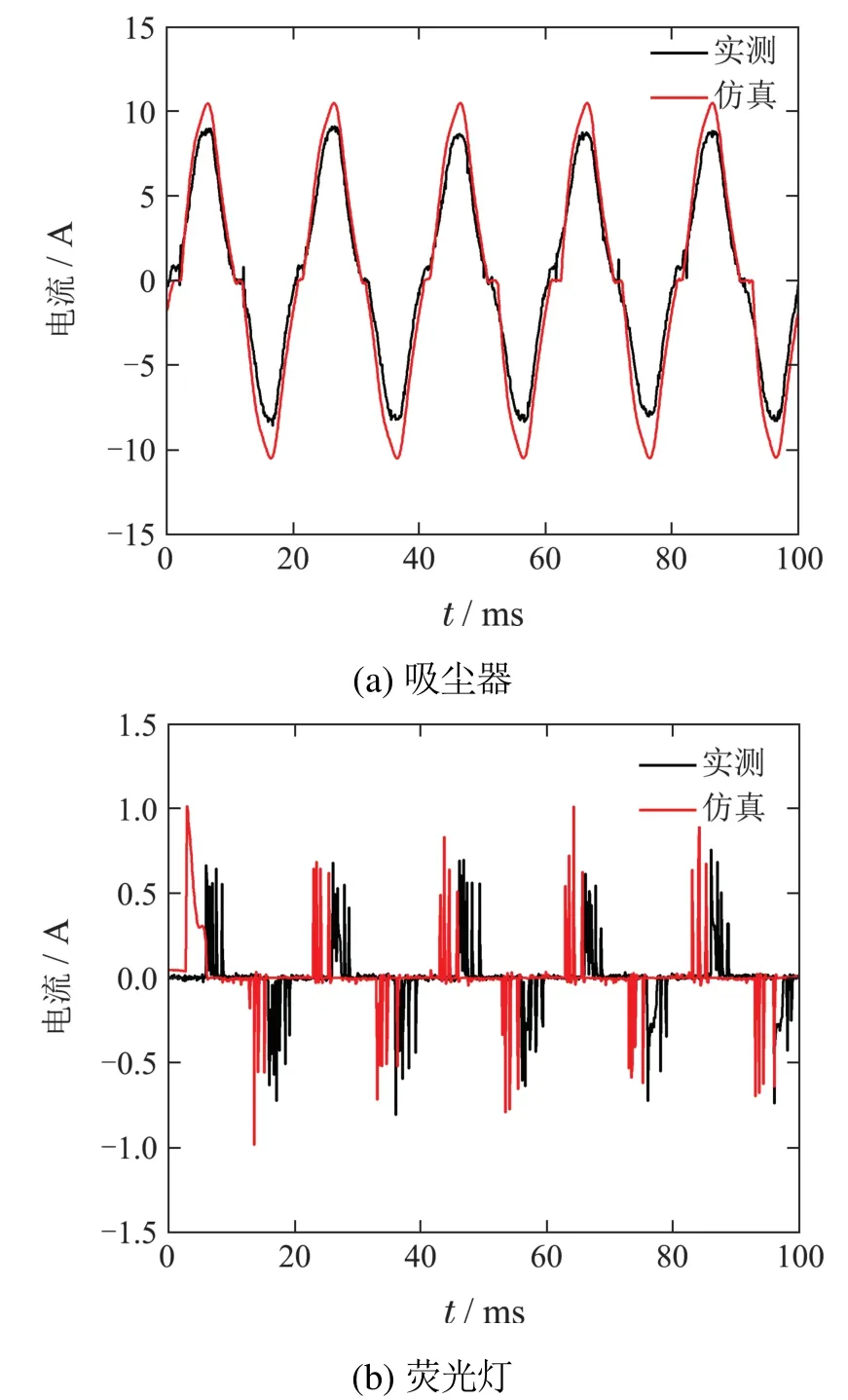
图4 电弧电流仿真波形与实测波形对比(抗混叠滤波器截止频率均为5 kHz)Fig.4 Arc current waveforms comparison between simulation and experiment (filtered by a low pass filter with a cut-off frequency of 5 kHz)
3 串联电弧故障检测算法
为模拟实际嵌入式系统的调理电路,将仿真步长为1µs、仿真时长为100 ms 的波形经截止频率为5 kHz的二阶低通滤波器滤波后,以10 kHz的采样率提取保存.按此法对6种负载分别获取正常和燃弧状态下的负载电流样本各1000条.
3.1 特征提取
1) 基于Hurst指数的频域特征提取.
串联电弧具有高度的非线性和随机性,会引入大量的谐波,因此可选取频域特征实现检测.对波形进行快速傅里叶变换(fast fourier transform,FFT)可得到对应的频谱F(i).为消除电流幅值对检测特征的影响,按式(4)对F(i)进行归一化得到幅值归一化FFT频谱FN(i)(简称归一化频谱):

其中n为频谱F(i)的总长度,结果如图5所示.可见串联电弧的存在导致谐波增多,归一化频谱包络陡峭程度降低、幅值下降的趋势变缓.由于非线性负载特别是电力电子负载自身存在的谐波污染,难以通过谐波之间的幅值运算构造合适特征予以描述,因此探索通过引入Hurst指数对这一现象进行表征.


图5 6种负载故障前后归一化频谱的变化Fig.5 The variety of normalized spectrum of six load waveforms between working and arcing
Hurst指数(H)由英国学者H.E.Hurst发明,因其能较好地反映时间序列数据的随机性而广泛用于各领域研究中.H取值范围为0~1,并按0.5划分为3个子区域,各区域具有如下所示含义:
1)H=0.5,表示输入序列具有显著的随机性;
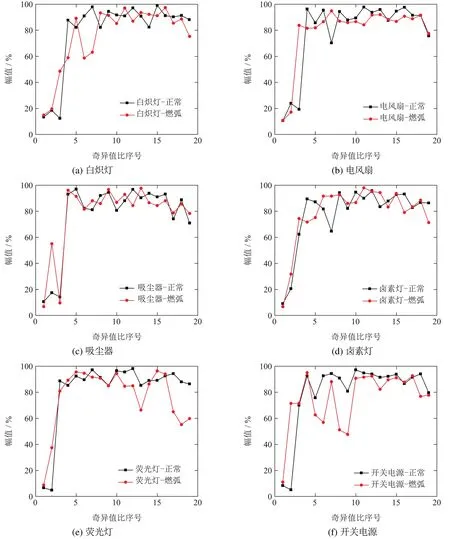
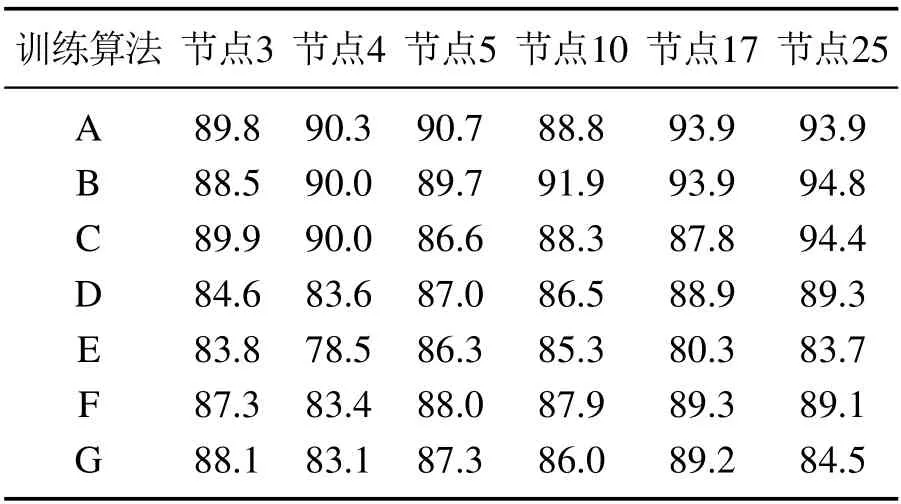
2) 0.5 3) 0 观察知,故障前后0~2500 Hz范围内的归一化频谱变化较为显著.故提取0~2500 Hz内的整数次谐波构成样本波形,按rescaled range analysis(R/S分析法)计算各负载故障前后Hurst指数变化如图6所示.图中吸尘器和开关电源故障前后Hurst指数波动范围重叠区域较小,可通过阈值判别正常工作与燃弧状态.部分负载如白炽灯、卤素灯和荧光灯在故障前后的Hurst指数波动范围出现部分重叠,但仍能对故障状态做出判断.这是由于电弧模型的燃弧剧烈程度相对偏弱且存在随机性所致.电风扇负载故障前后Hurst指数范围存在大范围重叠,无法检测电弧故障,其原因是负载电流小、燃弧剧烈程度弱,致使电流波形畸变小、频谱特征不显著.综上,Hurst指数能较好地降低频域特征复杂度,但单凭Hurst指数无法准确检测全部负载的串联电弧故障. 图6 负载故障前后Hurst指数的变化Fig.6 The variety of Hurst index before and after series arc faults on loads 2) 基于奇异值分解的时域特征提取. 串联电弧的非线性特性会引起负载电流的显著畸变.若将电流样本重构为二维矩阵,则电流波形的变化会导致矩阵数学特征的改变.奇异值是矩阵最显著的特征,可用于构造时域特征辨识串联电弧故障.因此,将单条电流波形按式(4)重构为20×50的波形矩阵A: 其中:i为行数,i=1,2,···,20;j为列数,j=1,2,···,50;It为单条电流波形样本,总长度为1000点.对波形矩阵A进行奇异值分解(singular value decomposition,SVD),将获取的20个奇异值按幅值降幂排列构成奇异值向量S.为消除电流幅值对检测特征的影响,按式(6)将S进行重构为奇异值比值向量Sr: 式中i=1,2,···,19. 6种负载故障前后的Sr变化情况如图7所示.由于均为线性负载,白炽灯和电风扇在Sr3,Sr4和Sr73个比值上呈现较显著的变化.吸尘器在故障前后Sr2变化显著.对于卤素灯,Sr4,Sr5,Sr6和Sr7在故障前后变化相对显著;荧光灯可用比值Sr2,Sr17,Sr18和Sr19表征燃弧与否;开关电源的比值Sr2,Sr5,Sr7和Sr8对电弧故障较敏感,可以用于故障检测.综上分析可知,故障前后不同负载的奇异值比值敏感序列难以统一,这些敏感序列故障前后的变化范围和趋势也存在差异,因此将Sr中的19个元素全部选为时域特征作为后续算法的输入. 图7 6种负载故障前后奇异值比特征的变化Fig.7 The variety of singular values of six load waveforms between working and arcing BP神经网络是一种训练算法成熟、广泛应用的人工神经网络,能在嵌入式系统中快速运行.其典型结构如图8所示,由输入层、隐层和输出层组成.隐层数目为1~2层,激活函数为sigmod函数或双曲正切函数.输出层节点数按结果分类的需求设定,激活函数采用线性函数.训练时算法从后向前依次调整每层节点激活函数的权值,直至输出误差小于给定值. 图8 典型BP神经网络结构Fig.8 Structure of BP neural network 本文中BP神经网络的输入特征向量维度为20,由奇异值比值Sri,i=1,2,···,19和Hurst指数构成;输出向量维度为1.较多的隐层数有利于提高准确率,但嵌入式平台的计算能力有限,应尽量减少网络计算量.因此隐层数目确定为1.当前隐层数目尚无确定的计算公式,可参考式(7)–(11)计算经验取值范围: 式中:Nhid为节点数,Nin为输入特征维度此处为20;Nout为输出结果维度,此处为1;Nc为结果分类个数,此处为2. 根据式(7)–(11)初步确定隐层节点数范围后,采用sigmod函数作为激活函数、结合不同的训练算法进行了筛选,结果如表2所示. 表2 不同隐层节点数及训练算法对应的准确率Table 2 BP network accuracy of varies combination between hidden layer nodes and training algorithms % 表中训练算法对应如下: A:Levenberg–Marquardt算法 B:贝叶斯规则法 C:BFGS拟牛顿法 D:弹性BP算法 E:归一化共轭梯度法 F:Powell–Beale共轭梯度算法 G:Polak–Ribiers共轭梯度算法 显然,节点数为25、采用贝叶斯规则法训练得到的BP网络准确率最高,为94.8%;节点数为17、采用Levenberg–Marquardt算法或贝叶斯规则法训练得到的BP网络准确率次之,为93.9%.为缩短计算时间,不宜因追求较高的诊断准确率而大幅增加节点数目,故确定隐层节点数目为17. 综上,串联电弧故障检测算法采用单隐层BP神经网络实现,其隐层节点数为17,输出层节点数为1,激活函数采用sigmod函数,总体准确率为93.9%. 将训练完成的BP 神经网络检测算法移植于STM32F767 平台(ARM Cortex–M7 内核,运行频率216 MHz),同时使用雅可比迭代法提取奇异值特征、FFT计算了Hurst指数特征.本文检测方案的运行时间测试结果如表3所示. 表3 基于STM32F767平台的检测方案实时性测试结果Table 3 The real-time experiment result on STM32 F767 结果表明,文中方案“采样+计算”时长为119.85 ms,即电弧存在后0.12 s内完成检测,满足UL-1699标准中最小检测时间为0.12 s的要求. 1) 本文基于Mayr模型增加了弧柱电感、间隙电容和压控随机开关,从而模拟电弧重燃现象及由此引起的高频振荡波形,并构建了白炽灯、电风扇、吸尘器、卤素灯、荧光灯和开关电源等典型负载的电路模型,尤其关注了电机和电力电子类负载的精准化建模,为串联电弧的特征提取奠定了基础. 2) 通过比对正常和燃弧状态下的负载电流波形,本文提出电流波形矩阵的相邻奇异值比值作为时域特征和0~2500 Hz内谐波占比序列的Hurst指数作为频域特征.当故障发生后,0~2500 Hz范围内的归一化频谱波形较之负载正常工作时呈现更显著的平缓趋势即长期记忆性,基于0~2500 Hz范围内的谐波占比计算得到的Hurst指数可较好地判断串联电弧的发生情况. 3) 本文基于BP神经网络实现了单负载串联电弧故障检测,总体准确率达93.9%.检测方案在STM32 F767平台上计算时长为19.85 ms,证实了该检测方案和特征参数的有效性,有助于串联电弧检测的工业化应用和实施.


3.2 基于BP神经网络的故障检测算法


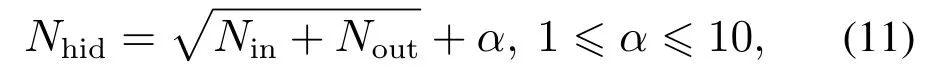

4 结论

