质子交换膜燃料电池系统数字孪生故障诊断模型研究

朱 静,赵静欣

(南京航空航天大学自动化学院,江苏南京 211100)

1 引言

作为最有前景的绿色能量转化装置,将氢能通过电化学反应转换为电能的质子交换膜燃料电池(proton exchange membrane fuel cell,PEMFC)被广泛应用于航天飞行器、潜艇动力源、汽车和电站[1].然而,PEMFC由传感器、压缩机等复杂零器件构成,这些设备会带来一定的非线性和不确定性[2],因此PEMFC往往容易出现降低系统性能甚至缩短电池寿命的故障.这些可能发生的故障分为传感器故障、组成成分故障和执行器故障[3].作为PEMFC系统中重要的执行机构,空气供应子系统易发生的故障主要有压缩机喘振、压缩机停转、空气管道泄漏,而这些故障对燃料电池的稳定运行影响甚大.电堆作为燃料电池中核心部件,承担着能量转换的重要任务,然而膜干和水淹等故障会直接影响能量转换效率甚至造成燃料电池的永久性损伤.因此,对上述故障进行故障诊断是保证系统稳定、高效运行的关键.

作为系统运行中监控程序的故障诊断包含了两个子任务:故障检测和故障隔离.前者是对有无故障的检测,后者则是对故障类型的识别[4].在过去的几十年内,故障诊断方法已在燃料电池系统中广泛地应用和发展[5].基于等价空间法,文献[6]通过解析冗余关系(analytical redundancy relation,ARR)将燃料电池的数学模型线性化为8个状态表达式,进而利用故障敏感度矩阵完成了对燃料电池膜干、水淹和空压机过电压这3种故障的诊断.通过线性变参数(linear parameter varying,LPV)观测器的方法,文献[7]首先通过残差和阈值的比较进行故障检测,然后通过相对故障敏感度的方法进行故障隔离.然而该观测器是根据工作点通过Jacobian线性化来完成,其较难应用在实时环境中[8].基于参数辨识模型,文献[9]在R(RQ)(RQ)(RQ)三阶等效电路拟合的电化学阻抗谱(electrochemical impedance spectroscopy,EIS)的基础上,利用PSO–SVM分类方法完成了对电堆中膜干和水淹的故障诊断.基于黑盒模型的文献[10]则是通过Elman神经网络建立燃料电池的模型完成了水淹故障的诊断.以上所述的故障诊断方法的应用均是基于模型,而上述模型的建立或是通过复杂的物理方程,或是通过大量的数据推理,但基于两者结合建立更为精确实时的模型的故障诊断方法在质子交换膜燃料电池中鲜有研究,而精确实时的模型则是复杂的燃料电池装置在多变的运行环境下实时高精度的故障诊断与健康预测所必要的.

依托于物联网的高速发展,近年来数字孪生(digital twin,DT)技术受到国内外越来越多的关注.数字孪生概念首次由美国国家航空航天局在2010年为实现飞行系统的全面诊断与维护提出的[11].数字孪生是在信息空间内建立的物理系统的数字化模型映射,其利用传感器数据的智能化传输与分析,形成多尺度、多物理量、多概率的仿真过程[12].2012年,美国空军提出建立的基于历史数据、仿真模型和实时传感器数据的数字孪生体用在了飞行器的故障诊断、健康诊断及寿命预测中[13].此后,数字孪生在多个场景的应用引起了广泛的关注.正值“十四五”的当下,数字孪生在智慧能源系统中得以应用,以解决智慧能源所面临的技术壁垒[14].在质子交换膜燃料电池领域,文献[15]开发了其多物理场的数字孪生模型.但是到目前为止,鲜有基于数字孪生的故障诊断研究.

基于以上的分析,本文提出了一种应用于质子交换膜燃料电池的基于数字孪生技术的故障诊断方法,建立基于数字孪生估计器的平行故障诊断模型,并给出数字孪生中数据传输与分析的物理架构和具体实现过程.本文的主要贡献及创新点列举如下:1)给出相较于传统模型[16]更为准确、实时的PEMFC空气供给系统的数字孪生体系统,为整个PEMFC系统的数字孪生体系构建作出了有效补充.2)提出基于数字孪生技术的故障诊断方法,该方法包含故障检测和故障隔离两部分,可以实现故障的快速、高效诊断.3)给出数字孪生中数据传输与分析的实现,并针对传输过程中可能会出现的数据丢包、错序等问题提供了有效解决方案.

本文其余部分结构安排:第2节为数字孪生估计器的建立,包括质子交换膜燃料电池空气供应系统的模型介绍及相对应的数字孪生估计器的建立.第3节给出基于数字孪生的故障诊断方法,包括故障检测和故障隔离两部分.第4节给出验证方法可行性的仿真结果.第5节讨论数字孪生中数据传输与分析实现的物理架构,并在最后第6节给出结论.

2 PEMFC数字孪生体系统

2.1 空气供应子系统动态模型

考虑PEMFC空气供给子系统采用以下四阶动态模型:

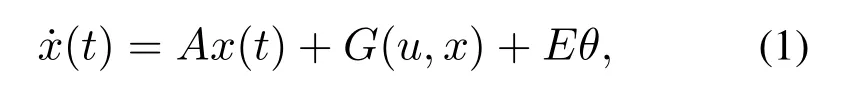
式中状态变量x=[pcppN2ωcppsm]T所代表的物理含义参考表1.

表1 燃料电池系统的关键物理量Table 1 Key physical quantities of the PEMFC system

系统(1)中的相关矩阵定义如下:

和

应注意的是系统矩阵A ∈R4×4是常量矩阵,G(u,x)∈R4×1具有Lipschitz 连续性,其表达式中的Wca,out为阴极侧的空气流动比.E ∈R4×1为已知的常量矩阵.系统的输入u=vcm为压缩机的电压,θ=Ist表示系统的扰动,其表现形式为燃料电池负载端的电流.系统的输出y(t)为

上述中所有的参数ci,i ∈{1,···,19}均为正常数,具体数值可参阅文献[16].

2.2 数字孪生估计器

数字孪生估计器的建立可通过基于模型的方法或数据驱动或两种方法的结合[17–18].本文使用基于模型的方法建立数字孪生估计器,并将传感器数据通过特定的数据传输与分析(见第5节)后更新相应的温度参数.作为所提出的故障诊断方法中主要组成成分的数字孪生估计器如图1所示,其中数据传输阶段是将传感器测得的相关数据及所需的燃料电池系统输出数据y(t)传输给数字孪生体,用于构建较为精确的数字孪生估计器,而信息传输阶段则是将数字孪生体的输出与实际系统的输出作对比,借于此所进行的故障诊断及寿命预测则是对燃料电池系统的运行加以监管.

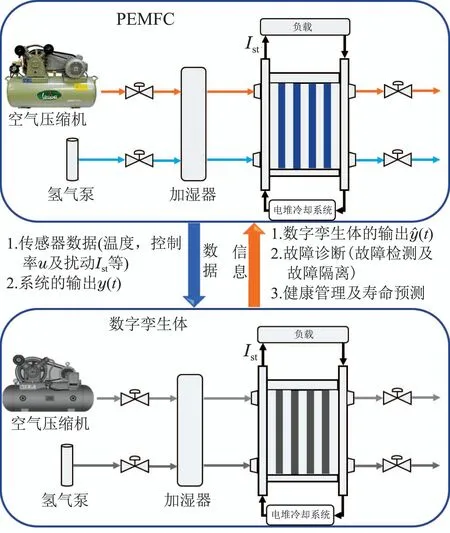
图1 基于数字孪生的质子交换膜燃料电池故障诊断方法实现的原理图Fig.1 Implementation of DT-based fault diagnosis in PEMFC systems

应当注意到的是估计器中的参数c1,c3,c7和c8将按照温度传感器数据更新,具体实现方式如图2所示的流程图.

图2 参数ci更新方法流程图Fig.2 Flow chart of update method for parameters ci

3 基于数字孪生的故障诊断

本节分两小节介绍基于数字孪生估计器的故障检测和故障隔离.故障检测即检查系统的输出与估计器的输出之间的一致性,而故障隔离是对故障的辨识.

3.1 故障检测

作为故障诊断方法中第1步的故障检测是通过计算残差来完成,而残差的生成是通过计算估计器的输出与系统输出y(t)之间的差值:

故障检测是通过比较残差γ(t)和阈值τi来确定是否有故障发生,即当残差值大于阈值,即可判定系统发生故障.基于此,标记故障发生为1,得到如下评判:

注意到理想条件下为0或者实际条件下接近0的阈值是故障诊断的鲁棒性所必要的.鲁棒性意味着在模型不确定性和通信噪声存在的情况下仍能成功检测故障[19].鲁棒性的实现大部分可以通过建立如文献[20]中的自适应阈值来完成.由于本文中所使用的数字孪生估计器的高精度特性,基于统计技术所建立的阈值也能实现相同的目的.

3.2 故障隔离

在系统检测到故障后,故障隔离通过分析残差γ(t)与故障集f(t)=[f1(t),f2(t),···,fm(t)]之间的关系辨识可能发生的故障fj(t).通过利用FSM⊂γ(t)×f(t)来定义这两者之间的关系,此处的FSM即为故障敏感度矩阵(fault signature matrix,FSM)[19].故障隔离则是通过FSM中不同故障所对应的残差不同来实现.

然而上述基于FSM的故障隔离方法在实际应用中中会造成信息的丢失,并且按照FSM,复杂系统中有些故障会有相同的残差表现,这将会导致故障隔离失效[21].因此很有必要添加故障与残差之间的额外信息来完成故障隔离,比如响应时间或者敏感度[19].

基于以上考虑,本文采用残差故障敏感度来提升故障隔离性能.按照文献[22],敏感度函数描述如下:

上式定量定性地分析了故障对残差的影响.基于此,上述FSM所存在的问题得以解决.

在线故障诊断中,敏感度函数Sγ,f是在故障发生后所得到,注意到该值的计算需要知道或者近似地知道故障的定性定量的信息,而该信息的获取则需要较为复杂的比如文献[23]中所示的故障重构算法.为了解决这个问题,相对故障敏感度函数给定如下:

该式中的残差γk(t)应当确保此式有意义,即在故障发生后满足γk(t)0.为了下面分析方便特将该残差视为残差γ(t)中的第1个,即k=1.

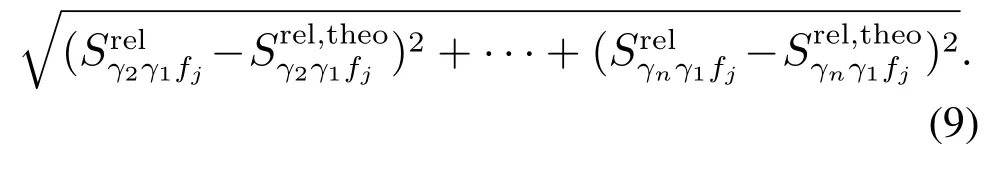
4 仿真分析

本节通过在仿真分析中引入定义在表3中的质子交换膜燃料电池中一些常见故障来验证故障诊断方法.在此给出故障f2和f4的诊断结果,并将故障f3的诊断作为与传统模型的对比试验,实验的最后给出关于混合故障的讨论.

故障f1仿真为压缩机内阻Rcm的增加.该故障首先引起扭矩τcm的变化:

式中:ηcm是电机的机械效率,kt和kv是电机的常量,vcm和ωcm分别是压缩机的电压和转速.其次,该故障也会导致定义在故障f4中的参数ksm,out变化[7].

故障f2仿真为控制器提供给压缩机的电压vcm的增量.该故障同样引起如式(10)中扭矩的变化.

故障f3仿真为阴极空气流动的变化:

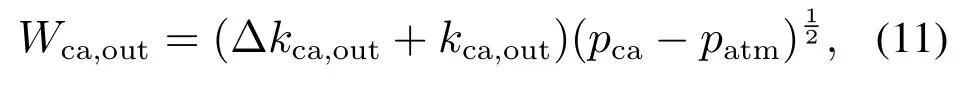
式中:kca,out为阴极输出常量,patm和pca分别为大气压强和阴极压强.

故障f4仿真为供应管道中气体的泄漏:

式中psm和pcp分别为供应管道和阴极侧的压强.

根据式(5),可以得到残差信号如下:

使用式(6)所描述的故障检测方法,通过仿真实验确定定义在表2中的故障是否影响残差.基于此,如表4所示的故障敏感度理论矩阵得以建立.通过该矩阵,发现故障f1和故障f2残差变化相同,两种故障不能隔离,同样地,故障f3和f4也不能够隔离.

表2 理论相对故障敏感度矩阵Table 2 Theoretical relative fault sensitivity matrix

表3 质子交换膜燃料电池中的故障Table 3 The faults in PEMFC

表4 故障敏感度理论矩阵Table 4 Theoretical fault signature matrix

为了解决上述问题,首先通过式(8)计算出理论相对故障敏感度矩阵如下表5所示,进而在实验过程中实时计算如式(9)所示的欧式距离,最小欧式距离所对应的故障即为可能发生的故障.

表5 相对故障敏感度理论矩阵Table 5 Theoretical relative fault sensitivity matrix

分别在30 s引入故障f2,f4.从图3可以看出,在t=30 s后故障引起4个残差超过阈值,故障检测显示发生故障.如图4所示,在t=31 s之后,故障f2所对应的欧式距离趋于0,此时即可判定系统发生故障f2.类似地,如图5所示,3个残差在t=30 s后越过阈值,此时系统发生故障.图6 表明故障f4的欧氏距离在t=32.5 s后趋于0,此时即可判定系统发生故障f4.

图3 故障f2影响下的残差Fig.3 The residuals under the influence of f2

图4 欧氏距离Fig.4 Euclidean distance

图5 故障f4影响下的残差Fig.5 The residuals under the influence of f4

图6 欧氏距离Fig.6 Euclidean distance

针对参数ci,i ∈{1,3,7,8}变化过程中的故障诊断方法是否有效的问题和所提出的诊断方法比之传统的故障诊断方法是否有优势的问题,进行如下的仿真实验.需要说明的是传统方法为固定参数模型,本文提出的数字孪生模型的参数变化是按照图2所进行,其中采样周期T为15 ms,依托于图10的高速数据传输与分析,处理过程所需的时间为2 ms.仿真中温度Tfc从351.15 K开始每10 s增加1 K直至仿真结束.故障引入时间为t=30 s,选取故障f3为引入的故障是因为该故障对温度的变化较为敏感,这一点从系统模型(1)和式(11)得以体现.

从图7可以看出,在t=0 s至t=20 s内残差γ2低于阈值,此时判断系统发生故障,但实际情况中此时并没有发生故障,至此基于传统模型的故障检测方法失效,故障隔离亦失效.作为对比,图8和图9分别为本文方法在参数ci变化时的故障检测和故障隔离结果.图8所示的是基于数字孪生模型的故障检测结果,尽管在每次温度变化时残差信号γ2会有脉冲变化,但其时间短至可以忽略,不影响整体的故障检测结果.在系统运行至t=30 s之后,有3个残差越过阈值,此时判断系统发生故障.在图9所示的欧氏距离图中,故障f3所对应的距离在t=31 s后趋于0,此时系统可能发生故障f3.

图7 基于传统模型的故障f3影响下的残差Fig.7 The residuals under the influence of f3 based on the traditional model

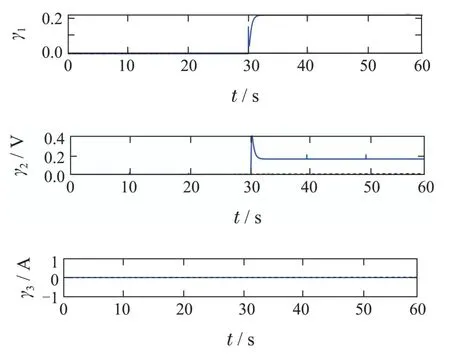
图8 基于数字孪生的故障f3影响下的残差Fig.8 The residuals under the influence of f3 based on the digital twin

图9 欧氏距离Fig.9 Euclidean distance

仿真实验的最后,讨论本文方法针对混合故障时的适用性.在故障检测阶段,若多个故障先后发生,则可通过残差信号的变化次数判断是否是混合故障,若多个故障同时发生,则可根据残差信号越过阈值的大小,并根据经验分析此时是否是混合故障.在故障隔离阶段,理论分析可知,在检测阶段已知混合故障可能由几种故障组成的前提下,取最小的几个欧式距离,其代表的故障即为可能混合的几种故障.但是在两种故障组成的混合故障的实验仿真后发现,此法可能会发生误判的情况,尽管能够隔离出混合故障中的一种,但对于第2种故障会发生为误判成其他故障的情况.该误判情况发生的原因可能是故障隔离阶段为数值的运算,若混合故障的相对故障敏感度函数的值与某一种故障的值接近,那么误判情况会发生.针对这种情况,可采用的解决方案为:首先可通过增加残差的数量,以此获得包含混合故障的不同故障的更多残差表现,以实现混合故障的检测及隔离;其次可通过故障树结构建立较为完备的包含可能发生的混合故障的故障库,以提高隔离阶段的准确率.

5 PEMFC平行故障诊断系统的物理实现

基于模型和数据驱动结合的数字孪生模型能够实现真实的虚拟映射[14].以模型为基础,通过高效的数据传输与处理,数字孪生模型得以迭代和优化,进而质子交换膜燃料电池的虚拟映射得以实现.图10给出了本文所构建的PEMFC平行故障诊断系统的物理架构.

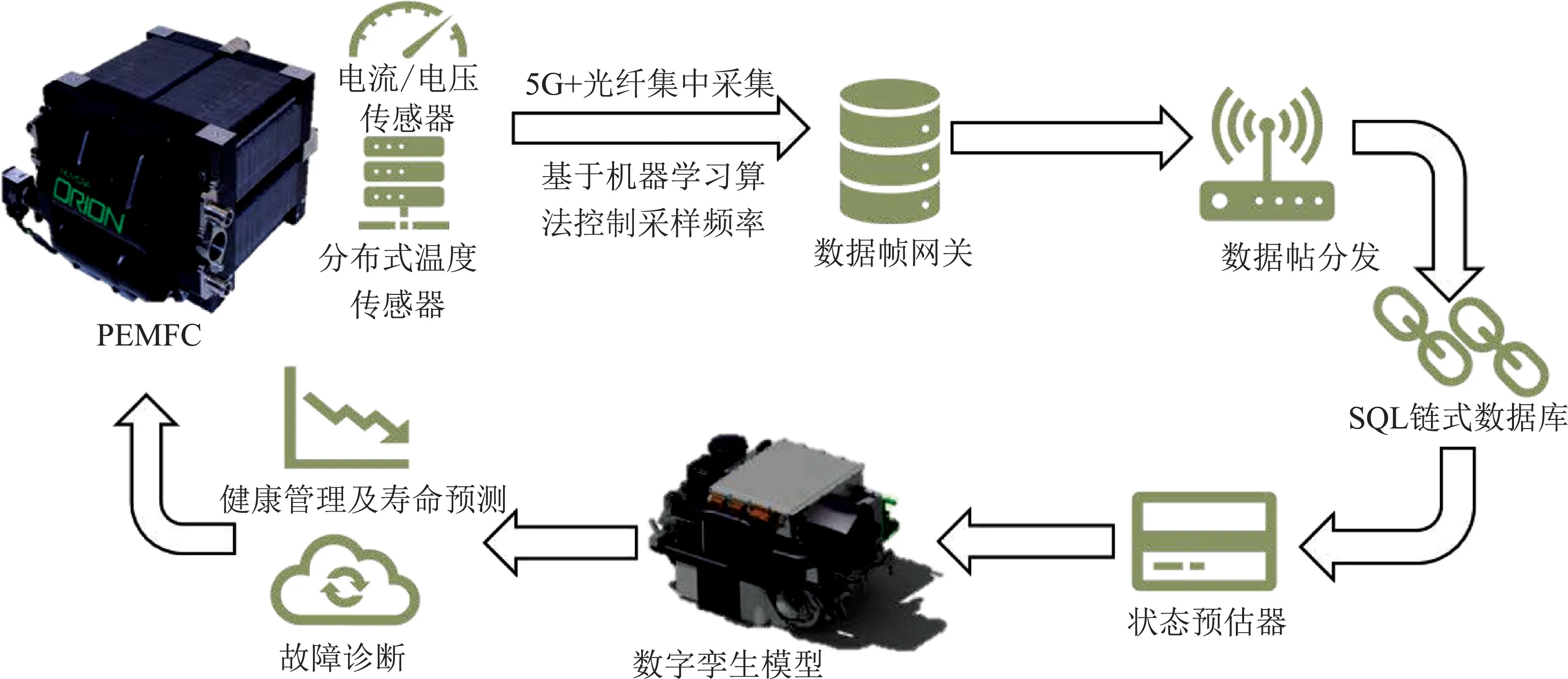
图10 数据的采集、传输和分析Fig.10 Data collection,transmission and analysis

在实际的搭建中,首先通过先进传感器采集到的多模异构数据在PEMFC系统的本地侧实时规范化.数据的采集通过智能化的机器学习算法控制其采样频率.进而采用高速、低延的网络通信协议进行传输,并存储于操作数据方便的结构化查询语言(structured query language,SQL)链式数据库中.值得注意的是在数据传输过程中尽管采用的是高效、低延的传输,但仍不可避免的存在数据丢包、时延等问题[24],因此本文增加状态预估器[25]以补偿PEMFC系统到数字孪生体之间的时延,从而为时延和数据丢包问题提供有效的解决方法.在获得数字孪生模型后,通过相关数据进行对比、处理,完成设备中的故障诊断,并对PEMFC系统形成全生命周期的健康管理及寿命预测方案生成.这样,获得的运行状况能够对质子交换膜燃料电池进行实时地监管,为其安全、可靠的运行提供有力保障.

6 总结

正值物联网高速发展及能源转型之际,数字孪生技术为复杂的质子交换膜燃料电池的故障诊断及寿命预测提供新的思路.本文所提出的基于数字孪生技术的故障诊断方法依托于基于模型和数据驱动所搭建的数字孪生估计器,依据残差是否越过阈值来检测故障,由于某些故障会表现为相同的残差变化,因此在故障隔离阶段通过相对故障敏感度来解决该问题,在仿真中通过引入4个较为常见的故障验证了故障诊断方法的有效性.最后,本文关注数字孪生模型的数据的传输与分析问题,给出了相关平行故障诊断系统的物理实现结构,有效保障了PEMFC系统的安全可靠运行.目前完成的质子交换膜燃料电池空气供应系统的数字孪生可为下一阶段整个更复杂的质子交换膜燃料电池的数字孪生体的补充,以期在以后的研究中通过故障树建立更为完备的故障库,以诊断更多、更复杂的故障类型.