用于永磁同步电机周期性转速脉动抑制的重复控制

张巧芬 ,刘彦呈 ,郭昊昊 ,张峰魁 ,郭 晨

(1.大连海事大学船舶电气工程学院,辽宁大连 116026;2.大连海事大学轮机工程学院,辽宁大连 116026)

1 引言

永磁同步电机以其高效、高功率密度、高可靠性等优点,广泛应用于电动汽车、电力推进船舶、多电飞机等交通运输行业[1–2].电机输出转速平滑度是衡量牵引推进系统性能的重要指标,而电机控制系统中存在的多种非理想因素会造成电机稳态转速出现周期性脉动.这些非理想因素主要包括电流测量误差、逆变器死区效应、电机本体的齿槽效应和磁链空间谐波等[3–4].

电流测量误差分为偏移误差和增益误差两种,分别造成电机稳态转速出现1,2次脉动分量[5].文献[6]将高频电压信号注入电机,通过提取高频电流分量计算电流增益误差,然而该方法将引起电机高频抖振.文献[7]提出一种考虑外环控制器影响的偏移误差补偿方法,提高电机动态性能,然而该方法在电流控制器饱和时将失效.文献[8]提出一种估计电流误差的定点采样方法,然而该方法的应用受到其特殊硬件拓扑要求的限制.文献[9]提出一种相电流传感器自校正策略,但该方法需要改变电流传感器的常用接线方式,并且只能用于使用霍尔电流传感器的驱动系统中.从控制系统的角度出发,电流测量误差是内环反馈通道的扰动,可将其视为外环前向通道的周期性扰动[10].根据内模原理,传统PI控制器无法完美抑制周期性扰动信号,文献[10–13]通过在转速外环PI控制器并联谐振控制器,抑制电流测量误差、负载扰动造成的永磁同步电机转速周期性脉动.

逆变器死区效应和电机磁链空间谐波将引起电机相电流出现6k±1 次谐波,稳态转速出现6k次脉动[3–14].文献[15]分析了死区效应对不同坐标系下电压、电流的影响,使用d轴电流环积分输出补偿死区效应.文献[16]考虑逆变器吸收电容和寄生电容对死区效应的影响,对传统的基于脉冲死区补偿方法进行修正.文献[17]提出一种注入谐波电压抑制高速永磁电机运行时相电流中5 次和7 次谐波的方法.文献[3–4,18–19]在电流内环附加谐振控制器,抑制死区效应造成的电机转矩脉动.文献[20]利用傅里叶算法提取谐波信号并与重复控制器结合,抑制死区效应产生的6,12次谐波.

重复控制器可以看作是负比例增益项、积分项和一系列谐振控制器的组合,与并联结构的多谐振控制器相比,递归形式的重复控制具有更小的计算成本和设计复杂性[21].由于重复控制器可用于抑制多次谐波,近年来在电力电子领域得到广泛应用,如:并网逆变器[21]、模块化多电平变换器[22]、PWM整流器[23].然而,将重复控制器应用于永磁同步电机双闭环调速系统的转速外环,以同时抑制电流测量误差、逆变器死区效应等非理想因素造成的转速脉动还鲜见报道.由于电机转速通常在宽范围内变化,这使得脉动频率的变化范围大.如何设计转速自适应的重复控制器,是在电机驱动系统中应用重复控制器必须解决的问题.

为解决上述问题,本文在转速外环设计一种自适应重复控制器,以抑制由于电流测量误差、死区效应等非理想因素引起的永磁同步电机稳态转速脉动.为保证系统的周期性扰动抑制能力和全局范围稳定性,设计带相位补偿的FIR滤波器和线性相位补偿器,并给出重复控制器的参数选取依据.为解决附加重复控制器带来的超调过大问题,将fal函数引入重复控制器,利用其大误差小增益、小误差大增益[24]的特性,减小电机动态调节过程的超调.实验结果表明,所提方法可有效抑制非理想因素造成的永磁电机转速周期性脉动.

2 非理想因素造成永磁同步电机稳态转速周期性脉动机理

2.1 非理想因素分析

永磁同步电机驱动系统的非理想因素主要包括:电流测量误差、逆变器非线性、磁链谐波、齿槽转矩等,本节主要分析这些非理想因素对驱动系统的影响机理.

2.1.1 电流测量误差

电流测量误差包括偏移误差和增益误差,其中偏移误差是指在电机真实电流叠加直流分量,主要由零漂、电流传感器的残余电流、运放偏差、AD转换器偏差等造成.由偏移误差引起的q轴电流误差为[5]

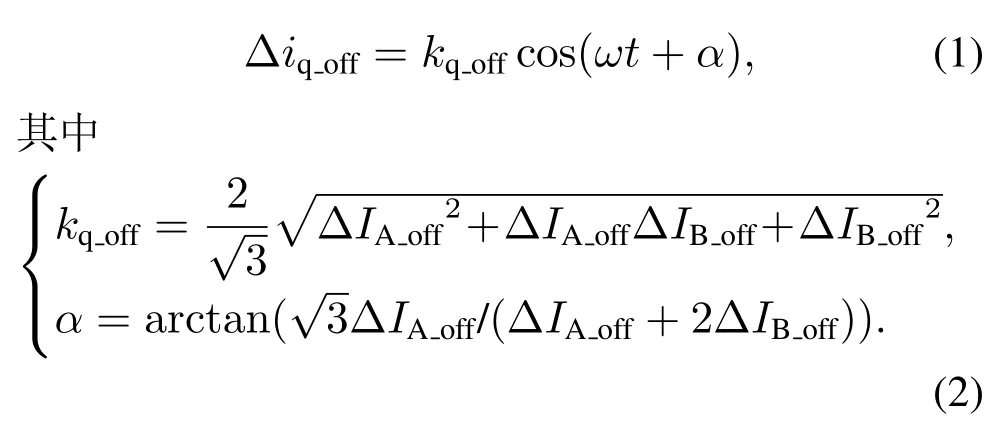
其中:∆IA_off,∆IB_off是A,B相偏移误差,ω为电机的电角频率.由式(1)可知,电流偏移误差将在q轴电流的反馈通道引入一次扰动分量.

电流传感器的输出需要经过调理电路来匹配AD转换器的输入范围.现代电机控制系统大多采用数字控制方式,在控制器中需要重新对AD转换结果进行定标,这些过程不可避免引入增益误差.由增益误差引起的q轴电流误差为[11]

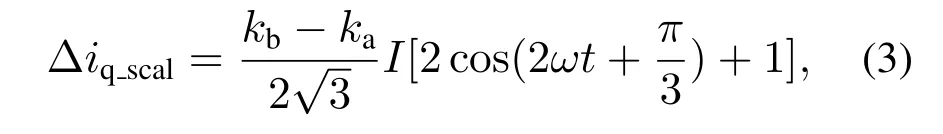
其中:ka,kb为A,B相电流增益系数.电流测量的增益误差将在q轴电流的反馈通道引入二次扰动分量.

2.1.2 逆变器非线性

逆变器非线性特性包括开关器件的固有特性(如电压降、导通/关断时间)和为防止上下桥臂开关管直通而设置的死区时间.逆变器非线性将在dq轴上引入6k(k=1,2,3,···)次谐波分量[25],其表达式为

其中Vdead为死区效应的等效扰动电压值,其大小取决于死区时间、导通/关断时间、开关周期和母线电压等,γ为电流空间矢量与q轴的夹角.

2.1.3 磁链谐波

另一种非理想因素是气隙中非正弦磁通密度分布引起的磁链谐波[11].考虑6n次谐波的dq轴磁链Φdm,Φqm表达式为

其中Φd0为d轴磁链的直流分量,Φd6n,Φq6n为6n次磁链谐波的幅值.磁链非正弦造成电机的反电动势出现6n次谐波,其对电机稳态转速的影响可归类在逆变器非线性效应分析中.

2.1.4 齿槽转矩

齿槽转矩Tcog是永磁体接近或离开定子齿时的磁阻转矩,与定子电流无关[11].其表达式为

其中Tn为n次齿槽转矩的幅值,Nco为电机槽数和极数之间的最小公倍数.

2.2 非理想因素引起转速脉动的机理

如图1所示为考虑非理想因素的永磁同步电机双闭环矢量控制框图,其中ωref和iq_ref分别是转速给定和q轴电流给定;ω和iq分别是电机转速和q轴电流;ierr是q轴电流测量误差;uq是q轴定子电压;∆uq是由死区效应和磁链谐波引起的q轴电压误差;kps,kis和kpc,kic分别是速度环和电流环PI控制器的比例系数和积分系数;Ks和Td分别是逆变器的比例系数和延迟时间常数;L和R分别是q轴电感和电阻;P是电机极对数;ψf是永磁体磁链;J是电机转动惯量;B是粘滞阻尼系数;TL是负载转矩.

根据图1,由梅森公式可以推导考虑电流测量误差、逆变器非线性与磁链谐波、齿槽转矩、负载转矩影响的电机实际转速表达式为

图1 考虑非理想因素的永磁同步电机双闭环控制系统Fig.1 Double closed-loop control system of PMSM considering non-ideal factors

从上式可得以下结论:1)电流测量误差引起的q轴电流1,2次脉动,将导致电机稳态转速出现1,2次转速脉动,逆变器非线性特性将导致电机稳态转速出现6k次脉动;2)对于电流测量误差,增大电流环控制器GC(s)的增益无法抑制ierr(s)对电机实际转速的影响,而增大速度环控制器增益却能有效抑制ierr(s)造成的转速脉动;对于逆变器死区效应和磁链谐波,增大GS(s)或GC(s)的增益均能抑制∆Uq(s)造成的转速脉动.然而,仅通过增大速度环或电流环PI控制器的增益来抑制非理想因素,效果是有限的.当PI控制器增益过大,会降低系统稳定裕度和抗高频干扰能力[10].因此,本文提出在速度外环设计插入式自适应重复控制器,增大速度外环控制器在扰动频率处的增益,从而有效抑制电流测量误差和死区效应等非理想因素引起的电机稳态转速脉动.

3 稳态转速周期性脉动抑制策略

3.1 基于插入式重复控制器的转速脉动抑制策略

为抑制上述非理想因素引起的多次(1,2,6,12)稳态转速脉动,本文将重复控制器插入转速外环,提高外环速度控制器在扰动频率处的增益,改进后的永磁同步电机在离散域的控制框图如图2所示.由于重复控制器可以提高系统在基频整数倍处的增益,因此这种控制策略可以同时抑制各种非理想因素引起的周期性扰动.

图2 引入插入式重复控制器的永磁同步电机控制框图Fig.2 PMSM control block diagram with plug-in repetitive controller

重复控制器的结构如图3所示,∆ω为速度误差,作为重复控制器的输入,urep_ref为重复控制器输出,krc为重复控制器增益,N=fs/f0(fs=2kHz为速度外环采样频率,f0为扰动信号的基频),Q(z)是低通滤波器用于保证系统的高频稳定性,L(z)用于补偿未添加重复控制器之前的原始系统滞后相位,以保证附加重复控制器后的系统稳定性.

图3 重复控制器结构Fig.3 Block diagram of the repetitive controller

重复控制器在离散域的传递函数为

3.2 重复控制器参数选取

令未加重复控制器前系统的开环传递函数为G(z),图2中控制框图的闭环传递函数的分母特征多项式为

将式(8)代入式(9),得

在设计重复控制器前,系统PI参数的设定已保证1+G(z)的特征根都在单位圆内.令未加重复控制器前系统的闭环传递函数为M(z),可得系统的稳定条件为

3.2.1 Q(z)设计

低通滤波器Q(z)主要有3种形式:接近1但小于1的常数,带相位补偿的FIR低通滤波器和带相位补偿的IIR低通滤波器.与选用小于1的常数相比,带低通滤波器的重复控制系统能有效抑制剪切频率内的低频谐波,同时又可保证系统的高频稳定性[22].线性相位FIR滤波器设计方便,可以通过非因果相位超前项进行精确补偿,实现零相位延迟,其表达式为

a0+=1,a0越大滤波器的截止频率越高,本文选择Q(z)=0.25z−1+0.5+0.25z属于这类滤波器.

3.2.2 L(z)和krc设计

系统在高频段的稳定性可由Q(z)保证,但在低频范围Q(z)近似为1,此时稳定条件式(11)可简化为|1−krcL(z)M(z)|<1,为保证系统稳定性,需要补偿原系统传递函数M(z)的滞后相位.本文选择线性相位补偿方法[26]L(z)=zm,该补偿器可在频率ω处提供θ=180◦mω/ωN的相位补偿,其中ωN为Nyquist频率,可得系统的稳定条件为

其中NM和θM分别为原系统闭环传递函数M(z)在角频率ω处的幅值和相角,本文选择L(z)=z20.重复控制器的增益krc应满足式(13),才能保证系统稳定.增益值越大,系统的转速脉动抑制能力越强,但是过高的增益将引起系统不稳定,本文选取krc=0.7.

3.2.3 系数N的选取

不同于其它重复控制器的应用背景[21–22,26],电机稳态转速的脉动基频随转速的变化而变化,因此N的取值应自适应转速的变化,其表达式为

其中:Ts是采样时间,round(x)为取整函数.在每个采样周期,根据电机的给定转速值动态更新重复控制器的N值.

本文使用MATLAB的模型设计理念开发电机控制程序,在Simulink中建立电机控制系统模型,通过代码自动生成工具,将生成的C代码下载到TI公司的F2837–9D芯片.为了改变重复控制器N的值从而实现对电机转速变化的自适应,将Simulink延时模块的延时长度由默认的Dialog改为Input port,并将式(14)的计算结果输入到该端口.

3.3 基于fal函数的改进式重复控制器

谐振控制器在谐振频率附近幅值急剧变化,容易造成Nyquist曲线接近临界点,增大系统的敏感度函数,这将使系统的动态调节过程振荡加剧、超调变大[27–28].重复控制器可视为一系列谐振控制器叠加[21],如何解决附加重复控制器后引起的系统超调过大,是必须解决的问题.

非线性fal函数具有快速收敛特性,其表达式为

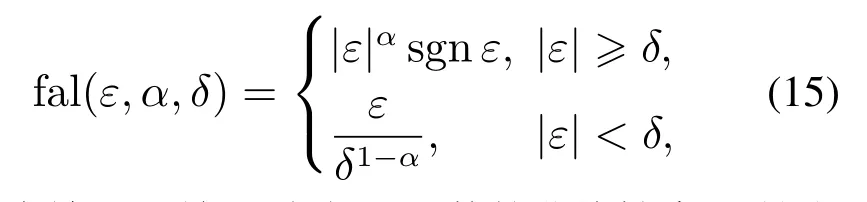
其中:ε为输入误差,α决定fal函数的非线性度,α越小非线性程度越大,δ决定线性段区间长度.为减小附加重复控制器后引起的系统动态调节过程转速超调过大问题,本文选取δ=0.4,α=0.6,与线性函数y=x的输出特性比较如图4所示.

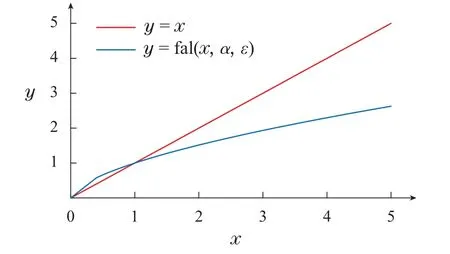
图4 fal函数与线性函数的输出特性Fig.4 Output characteristics of fal function and linear function

从图4中可以看出,fal函数能实现大误差小增益、小误差大增益,可有效解决引入重复控制器后系统超调过大的问题.结合fal函数的重复控制器结构如图5所示.

图5 结合fal函数的重复控制器Fig.5 Repetitive controller with fal function

4 实验验证

为验证设计的重复控制器对抑制永磁电机转速脉动的有效性,搭建如图6所示实验平台.测试电机和加载电机均为M–2310P–LN–04K型永磁同步电机,其参数如表1所示.电机由TI公司的DRV8305EVM驱动.相关实验数据通过开发的通讯程序采集到上位机.

图6 实验验证平台Fig.6 Experimental platform

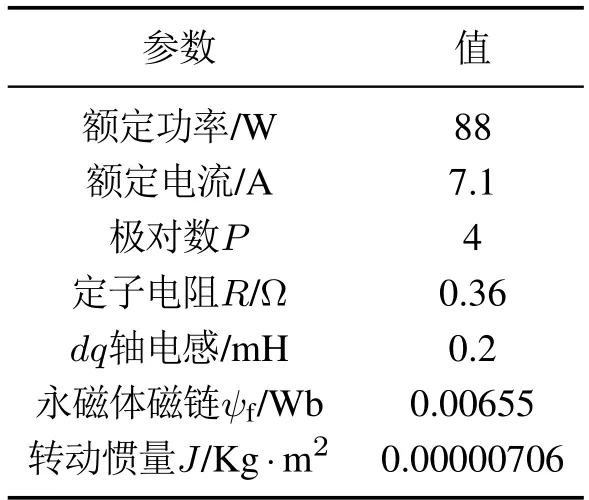
表1 永磁同步电机参数Table 1 PMSM parameters

4.1 非理想因素对永磁电机稳态转速脉动影响

为验证非理想因素对永磁同步电机稳态转速的影响,分别测试150 r/min,480 r/min,900 r/min下未加重复控制器时永磁同步电机的稳态转速,各转速的实验波形及其交流含量分析结果分别如图7–8所示.

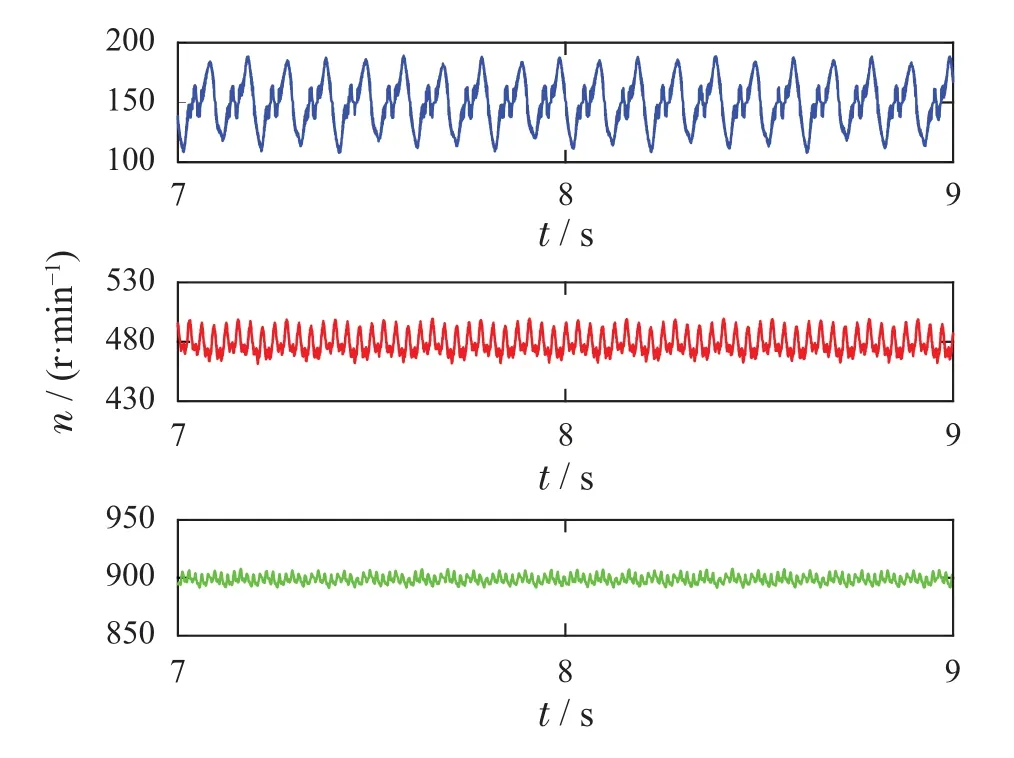
图7 未加重复控制器的永磁同步电机稳态转速Fig.7 Steady speed of PMSM without repetitive controller

图8 未加重复控制器的稳态转速1,2,6,12次脉动分量Fig.8 The 1st,2nd,6th,12th pulsating component of steady speed without repetitive controller

从电机的稳态转速波形可见:由于电机转动惯量的滤波作用[10–11],电机的稳态转速脉动随着电机转速的升高而趋于平缓,900 r/min时电机稳态转速交流含量已低至0.56%.从交流含量的分析结果来看,非理想因素会造成明显的稳态转速1次、2次和6次脉动,12次脉动不明显,且各次脉动分量随着电机转速升高而减小.故本文主要针对低速下(900 r/min以下)的电机稳态转速脉动问题设计转速自适应重复控制器.

4.2 稳态实验验证

为验证重复控制器的参数krc选取的合理性以及其在2π/(PωTs)为整数和非整数时的稳态效果,针对转速为300 r/min,150 r/min和780 r/min(前者2π/(PωTs)为整数,后两者2π/(PωTs)为非整数)开展实验研究.

图9和10为3种情况下(仅PI控制、带重复控制器krc=0.3和krc=0.7)电机稳态转速300 r/min的波形图及交流含量分析结果对比图.从实验波形可以看出,低速下仅PI控制电机稳态转速存在明显的转速脉动,交流含量为5.93%,1次、2次和6次脉动明显,而电机的稳态转速脉动可以通过所设计的重复控制器来很好地解决.可以看到,附加重复控制器之后,电机稳态转速脉动明显变小,各次脉动分量尤其是1次和2次明显降低.进一步对比krc=0.3和krc=0.7这2种情况,krc=0.7时总的交流含量以及1,2次脉动分量都优于krc=0.3,且系统仍保持稳定.可见krc=0.7的参数设计能在满足系统稳定的前提下保证控制器的转速脉动抑制能力.

图9 300 r/min稳态转速对比Fig.9 Contrast of steady state speeds at 300 r/min

图10 300 r/min稳态转速下的1,2,6,12次脉动分量Fig.10 The 1st,2nd,6th,12th pulsating component at 300 r/min

重复控制器在2π/(PωTs)为非整数时的稳态波形如图11 所示.从图中可见仅PI 控制时150 r/min和780 r/min的交流含量分别为18.71%和0.75%;增加重复控制器后,交流含量分别降为0.96%和0.32%.实验结果表明所设计的重复控制器在2π/(PωTs)为非整数时也能有效抑制由非理想因素引起的转速脉动.

图11 2π/(PωTs)为非整数时电机稳态转速波形Fig.11 Steady speed waveform of the motor when 2π/(PωTs)is a non-integer

4.3 动态实验验证

图12为重复控制器增益krc选择不同值时永磁同步电机从0到500 r/min的对比实验.由实验结果可知,krc=0.3时系统具有较小的超调,但稳态转速脉动抑制效果不佳,电机的稳态转速波动为494 r/min～506 r/min.而krc=0.7和krc=1时,转速脉动抑制效果大体相同,稳态转速波动范围约为498 r/min～502 r/min.但是krc=1时,电机的转速超调过大,约为30%.因此本文选择krc=0.7,兼顾系统的动态性能和稳态转速脉动抑制能力.

图12 不同krc的动态响应(m=20)Fig.12 Dynamic response with different krc (m=20)

放大图12中krc=0.7时的动态调节过程,可以看出实时转速相邻两个峰值之间的时间间隔约为30 ms(500 r/min对应的基波周期),这反映了重复控制通过记忆和累加来实现抑制效果的特性.当转速动态调节过程趋于稳定时,5.485～5.545 s之间的3个转速峰值波动明显减小.此外,图13为图12中krc=0.7时对应的重复控制器输出波形,图中正弦量的幅值逐渐放大至平稳,这同样反映了重复控制器对正弦量的累加作用.

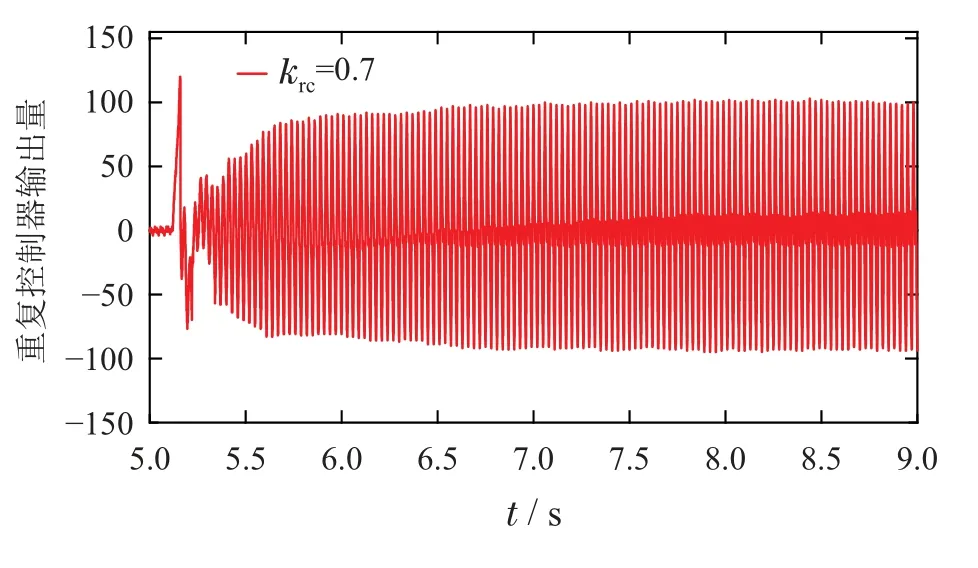
图13 重复控制器的输出波形图(krc=0.7)Fig.13 Output of repetitive controller(krc=0.7)

图14为重复控制器线性相位补偿系数m选择不同值时永磁同步电机从0到500 r/min的对比实验.由实验结果可知,3种不同m的取值,系统的稳态转速脉动抑制能力大体相同,调节时间也所差无几,但m=20时,系统的最大转速为580 r/min,相比其它两种m取值,具有较小的超调,因此本文选择m=20.

图14 不同m的动态响应(krc=0.7)Fig.14 Dynamic response with different m(krc=0.7)

影响重复控制器的另一个主要因素就是重复控制器的延迟系数N.转速变化时,N也发生变化.图15为转速变化波形图,转速分别从0 突变到400 r/min(N=75),550 r/min(取整后N=55),850 r/min(取整后N=35)和1150 r/min(取整后N=26).从实验结果可以看出N的变化并不会影响带重复控制器的永磁同步电机驱动系统的稳定性,且所设计的重复控制器可以自适应转速的变化,并具有良好的稳态和动态性能.

图15 给定转速变化时的实验结果Fig.15 Experimental results under speed change

图16为转速给定400 r/min带fal函数和不带fal函数的电机动态响应对比图.从实验结果可知,不带fal函数时,电机的最大转速为463 r/min,超调为15.8%;而带fal函数时,电机的最大转速仅为412 r/min,超调下降到3%.两种情况下电机的转速动态响应时间均为0.5 s左右.5.1 s突加50%额定负载,不带fal函数时电机的转速突降至320 r/min后最大转速可达455 r/min,而带fal函数时电机的转速突降至312 r/min后最大转速仅为430 r/min.

图16 转速给定400 r/min时带fal函数和不带fal函数的电机动态响应对比Fig.16 Contrast of dynamic response of motor with and without fal function at a given speed of 400 r/min

图17为转速给定600 r/min带fal函数和不带fal函数的电机动态响应对比图.从实验结果可知,不带fal函数时,电机的最大转速为720 r/min,超调为20%,而带fal函数时,电机几乎没有超调.5.1 s突加50%额定负载,不带fal函数时电机的转速突降至510 r/min后最大转速可达674 r/min,而带fal函数时电机的转速突降至506 r/min后最大转速仅为640 r/min.

图17 转速给定600 r/min时带fal函数和不带fal函数的电机动态响应对比Fig.17 Contrast of dynamic response of motor with and without fal function at a given speed of 600 r/min

从实验结果可以看出,电机转速和负载突变时,无论是否带fal函数,系统在经过一段调节时间后均可以很快恢复稳定状态,所设计的带fal函数的重复控制器可以有效解决由于引入重复控制器带来的超调过大的问题.

5 结论

本文针对电流测量误差、逆变器非线性效应等非理想因素造成永磁同步电机稳态转速低频周期性脉动问题,提出一种转速自适应重复控制器,将其插入永磁电机双闭环调速系统的转速外环,并设计了重复控制器的零相移FIR低通滤波器、线性相位补偿器和增益系数,在保证系统稳定性的前提下,兼顾转速脉动抑制能力和动态性能.针对附加重复控制器后,转速超调过大问题,引入fal函数,在不影响动态响应速度的前提下,有效降低转速超调.本文所提方法的原理在于增大系统在脉动频率处的增益,从而有效抑制系统的特定频率扰动.然而该方法只抑制了非理想因素对q轴电流通道的影响,而不能抑制其对d轴的影响.本文所提方法可拓展应用于内置式永磁电机、异步电机等不同电机驱动系统.