CEEMDAN在变压器振动信号提取中的应用

尚海昆,许俊彦,李宇才,林 伟

(现代电力系统仿真控制与绿色电能新技术教育部重点实验室(东北电力大学),吉林 吉林 132012)

1 引言

电力变压器将不同电压等级的电力传输线联结成网.但长期不间断运行,变压器不可避免的会发生各种异常甚至故障,影响电力系统的安全稳定运行,严重时还将带来巨大的经济损失[1–2].变压器现场运行环境下存在较大的噪声干扰,为得到真实可靠的振动信号,必须采取有效措施对现场干扰进行抑制[3–4].

目前用于振动信号检测的消噪方法有很多种,其中小波分析具有良好的时频分辨特性,非常适合于处理非平稳信号,在信号处理中得到了广泛的应用[5–6].文献[7]利用小波变换,提出了一种双小波去噪(double wavelet denoising,DWAD)方法,该方法能保留原始信号的更多细节.然而母小波和分解层次的人工选取使得小波方法在实际应用中受到一定限制.此外阈值选择是小波消噪方法的关键环节,选择不当会造成去噪信号发生畸变,直接影响消噪效果.

N.E.Huang提出了经验模态分解(empirical mode decomposition,EMD)方法,该方法把复杂信号分解为有限的固有模态分量(intrinsic mode function,IMF),是一种自适应的信号处理方法[8].由于EMD能够有效解决小波分析中参数的手动选择问题,在信号处理方面得到了广泛应用[9].文献[10]提出了一种改进的基于经验模态分解EMD的信号去噪方法.实验结果表明,该方法具有良好的去噪效果.然而EMD具有的模态混叠问题在实际应用中产生不利影响.为了解决该问题,N.E.Huang提出了集合经验模态分解(ensemble empirical mode decomposition,EEMD)方法[11].EEMD在待分解信号中加入高斯白噪声,并通过重复平均来消除.该方法可以有效地应用均匀分布特性来弥补信号尺度的缺失,解决模态混叠问题.文献[12]采用EEMD方法对变压器绕组故障情况下的振动信号进行了特征提取.然而EEMD算法未对残留噪声进行隔离,造成噪声信息的残留,影响后续的信号分析.

为了弥补了上述方法的不足并改善分解的完备性,Torres等人提出自适应白噪声的完整集成经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)方法[13].在该方法中,信号分解加入自适应噪声,通过改变分解过程,减少IMF中的残余噪声.该方法可以克服EEMD的缺点,并提高操作效率,较好地保留原始信号的信息.目前CEEMDAN在众多领域得到了广泛应用.文献[14]为了获取清晰的心电信号,提出了一种基于CEEMDAN算法的心电信号分析方法.结果表明,所提出方法能够同时消除高频干扰和低频基线漂移,与其他去噪方法相比具有更好的消噪性能.文献[15]为了实现对滚动轴承故障的早期检测,提出了基于CEEMDAN的故障诊断方法.实验结果证明了该方法适用于滚动轴承故障诊断与检测.文献[16]提出了一种基于CEEMDAN的旋转机械故障预测方法.结果表明,该方法在旋转机械故障预测方面优于同类方法.

本文尝试采用CEEMDAN对变压器振动信号进行有效分解,通过相关系数(correlation coefficient,CC)提取有效的IMF分量,然后对相关性高的IMF分量进行重构得到去噪后的信号.最后通过多种不同的指标验证该方法的有效性和实用性.

2 基于CEEMDAN变压器振动信号去噪

2.1 CEEMDAN简介

CEEMDAN是建立在EEMD基础上的一种信号分析方法,其分解原理如下:

设Ej(·)为经过EMD分解后得到的第j个IMF分量,CEEMDAN分解得到的第j个IMF分量为IMFj(t),wi为满足标准正态分布的高斯白噪声信号,ε为噪声的标准差,x(t)为原始信号.CEEMDAN分解的步骤如下:

1)将正负成对高斯白噪声加入到原始信号中得到新信号x(t)+ε0wi(t).对新信号进行EMD分解:

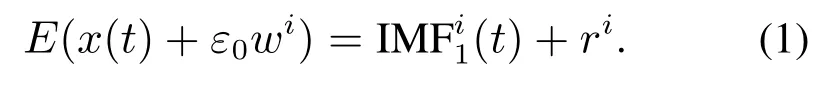
2)对产生的N个模态分量进行加总平均得到IMF1(t):

3)计算第1个残余分量r1:

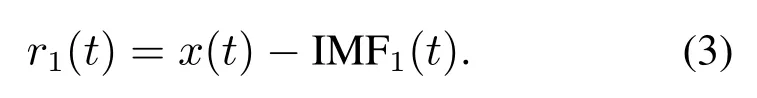
4)在r1(t)中加入正负成对高斯白噪声得到新信号,以新信号为载体进行EMD分解,得到IMF2(t):

5)计算第2个残余分量r2:

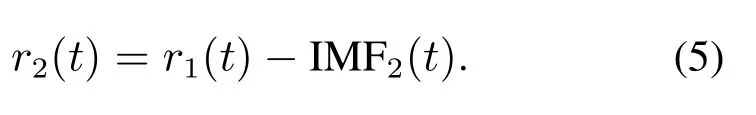
6)重复上述步骤,直到获得的残差信号为单调函数,不能继续分解,算法结束.此时得到的IMF分量数量为k,则原始信号x(t)被分解为

2.2 基于CEEMDAN变压器振动信号去噪步骤

本文首先采用CEEMDAN方法对原始变压器振动信号进行分解并提取IMF分量;其次,本文将CC应用于IMF分量的选择,提取出有效的IMF分量;最后,将提取出的IMF分量进行重构.具体的步骤如下:

1) 对初始变压器振动信号利用CEEMDAN进行分解并得出一系列的IMF分量;

2) 计算每个IMF分量的CC[17]:

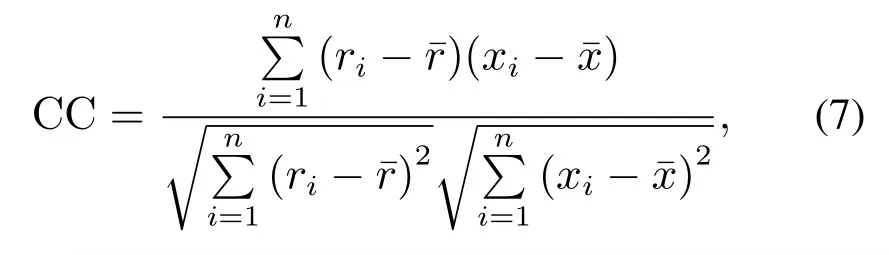
其中:CC是IMF分量与原始信号的相关系数,r是IMF分量,x表示变压器振动信号,n是IMF分量的数目.CC表示信号之间的相关程度,CC值越大,则r与x的相关性越大.若CC接近于0,则表明r与x的相关性较弱.

通过设定阈值θ,选取相关系数较大的IMF分量

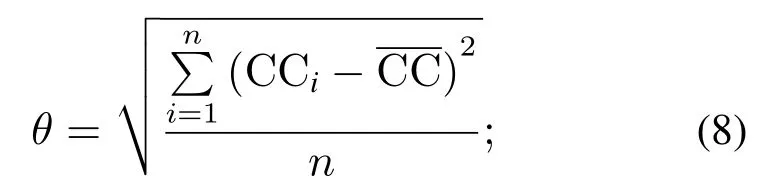
3) 对提取出的有效IMF分量进行重构.

本文提出的基于CEEMDAN变压器振动信号去噪流程图如图1所示.

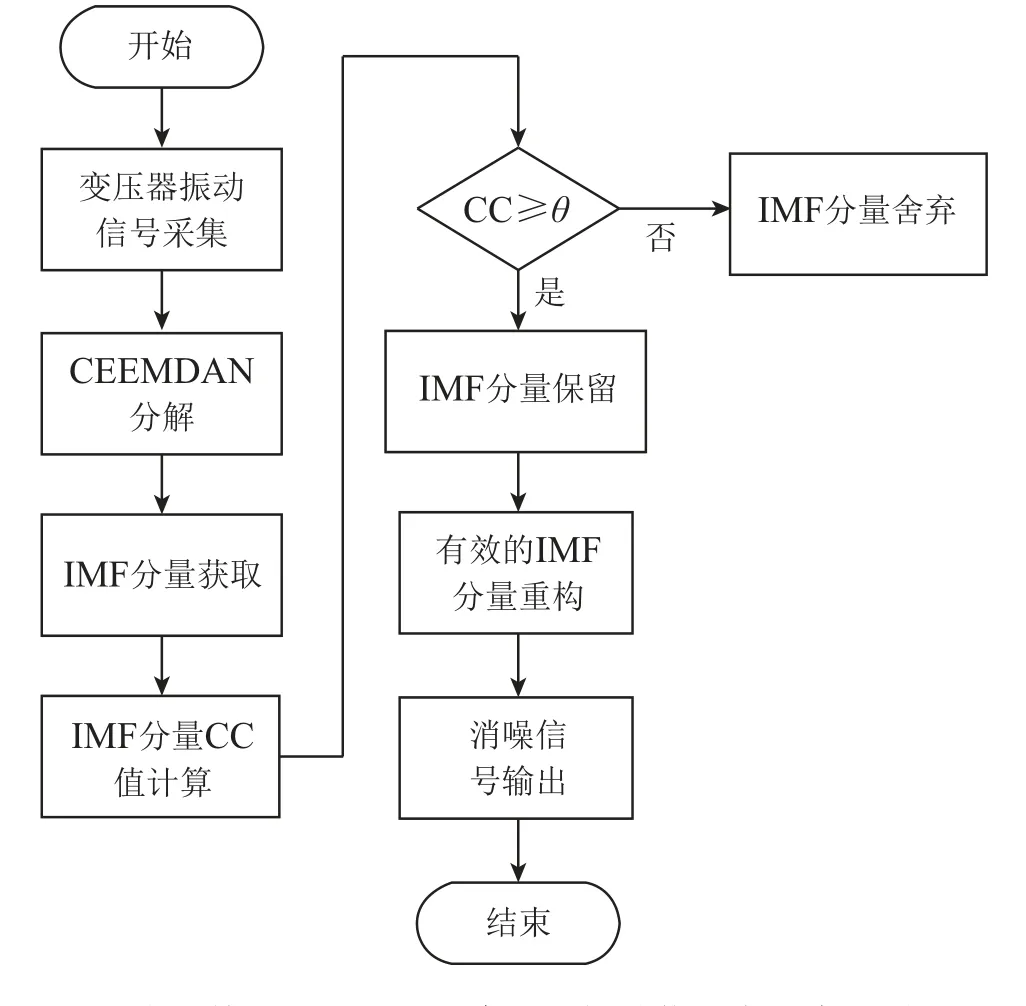
图1 基于CEEMDAN变压器振动信号去噪流程图Fig.1 A schematic diagram of transformer vibration signal denoising based on CEEMDAN

3 仿真分析

3.1 仿真信号模拟

本节通过仿真信号对基于CEEMDAN变压器振动信号去噪能力进行分析.根据变压器振动信号特征,构造出变压器振动模拟仿真信号.原始信号s(t)由3个函数组成,即f1(t),f2(t),f3(t),如式(9)所示.由于现场监测变压器振动信号受白噪声干扰的影响较为严重,为模拟现场真实振动信号,在原始信号上叠加了白噪声,满足高斯分布N(0,0.62).模拟变压器现场信号为s1,如式(10)所示.所对应的原始信号与染噪信号如图2所示.

由图2(b)可见,高斯白噪声掺杂在仿真信号中,无法直接对信号进行有效分析.为了验证本文所提方法的有效性,文中引入小波,EMD,EEMD方法对含噪声信号进行分析.为了量化消噪结果,本文采用信号的信噪比(signal to noise ratio,SNR)[18]、改进信噪比(improved signal to noise ratio,SNRimp)、均方误差(the mean square error,MSE)、均方根误差(the root mean square error,RMSE)、失真百分比(percent root distortion,PRD)对消噪质量进行量化分析[19–21].指标的定义如下:

图2 仿真信号Fig.2 Simulated signal

其中:s(i)表示原始信号,表示噪声消除后的信号,s1(i)表示染噪信号,n表示变压器振动信号的长度.SNR和SNRimp用来比较输入和输出信号之间的相似度,该值越大就说明去噪效果越好.MSE和RMSE体现输入噪声信号和去噪输出之间的误差,PRD反映去噪输出中存在的失真,MSE,RMSE,PRD数值越小说明原信号和去噪输出信号之间的差异越小,去噪效果越好.

3.2 小波方法参数配置

为验证所提方法的优越性,本文引入小波去噪方法.采用小波方法来对变压器振动信号进行去噪时,小波基选择主要考虑满足给定区间的紧支性和足够消失矩,而db(daubechies)小波是具有紧支性的正交小波基,且与变压器振动信号具有较高的相似性.因此本文选择db小波函数作为分析变压器振动信号的小波基.

首先固定小波分解层数为6,利用不同的阈值选取规则,对文中仿真信号进行处理.经过20次计算求均值,得到采用db 系列不同小波基消噪后的SNR,SNRimp,MSE,RMSE,PRD,如图3所示.

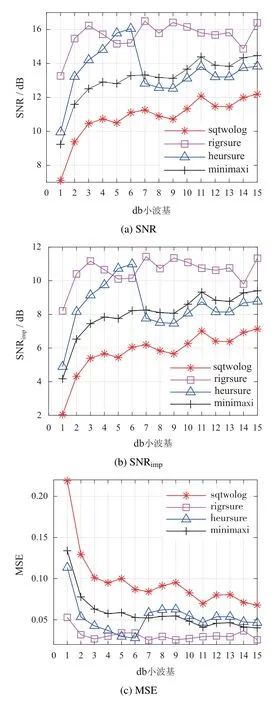
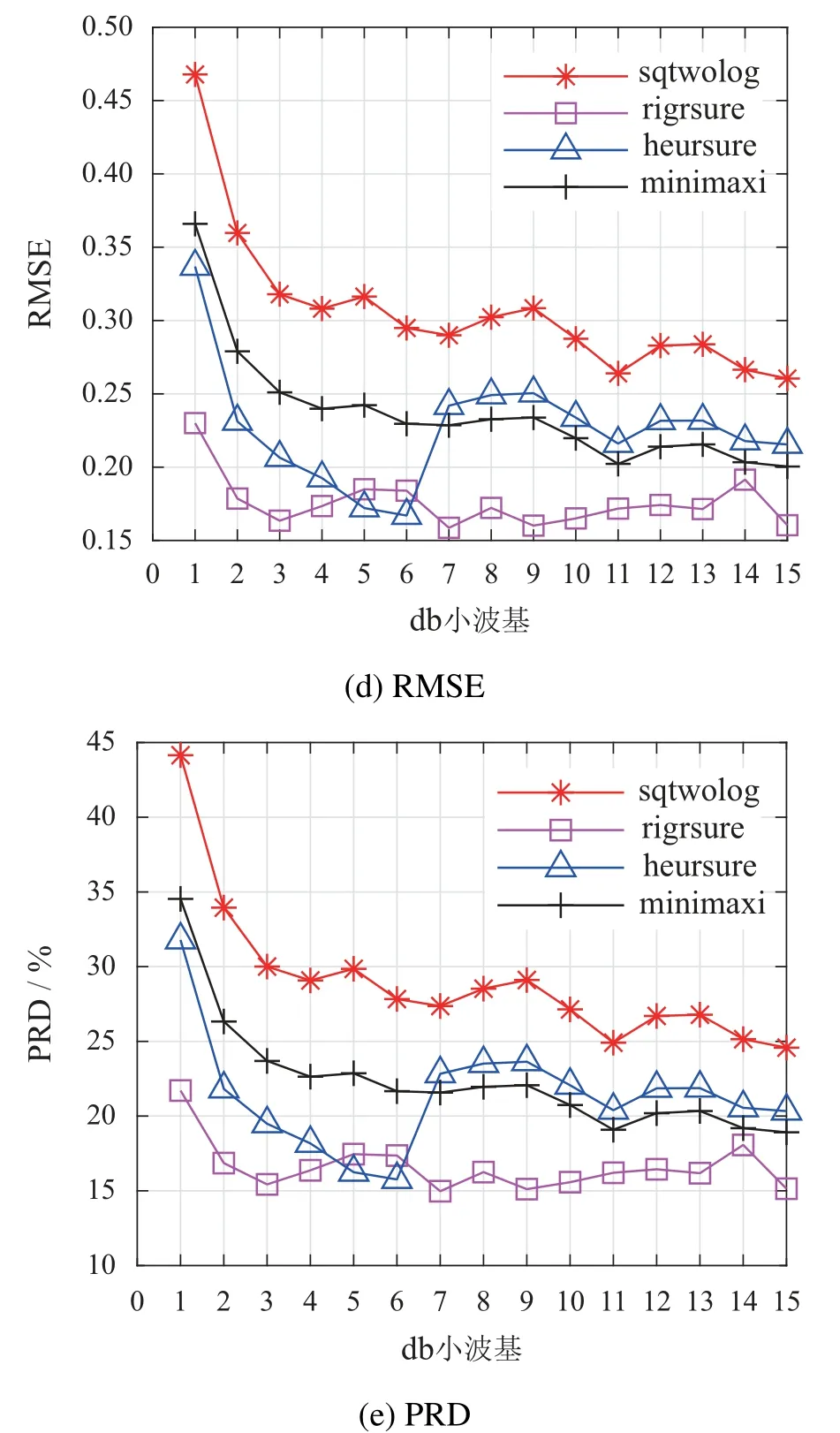
图3 采用不同db小波基消噪结果Fig.3 Denoised results based on different db wavelet

通过图3综合选取,对于sqtwolog阈值,db11小波基具有最大的SNR和最小的MSE,因此选择db11小波作为变压器振动信号的小波基.同理,选择db7小波作为rigrsure阈值的小波基,选择db5小波作为heursure阈值的小波基,选择db11小波作为minimaxi阈值的小波基.再固定最佳的小波基,采用不同的分解层数,经过20次计算求均值得到采用不同分解层数消噪后的SNR,SNRimp,MSE,RMSE,PRD,如图7所示.

图4 去噪结果显示,基于heursure 阈值去噪的SNR,SNRimp,MSE,RMSE,PRD均较好于另外3种小波,因此本文利用heursure小波阈值方法用于变压器振动信号提取,并选取db5小波基和4层分解层数.

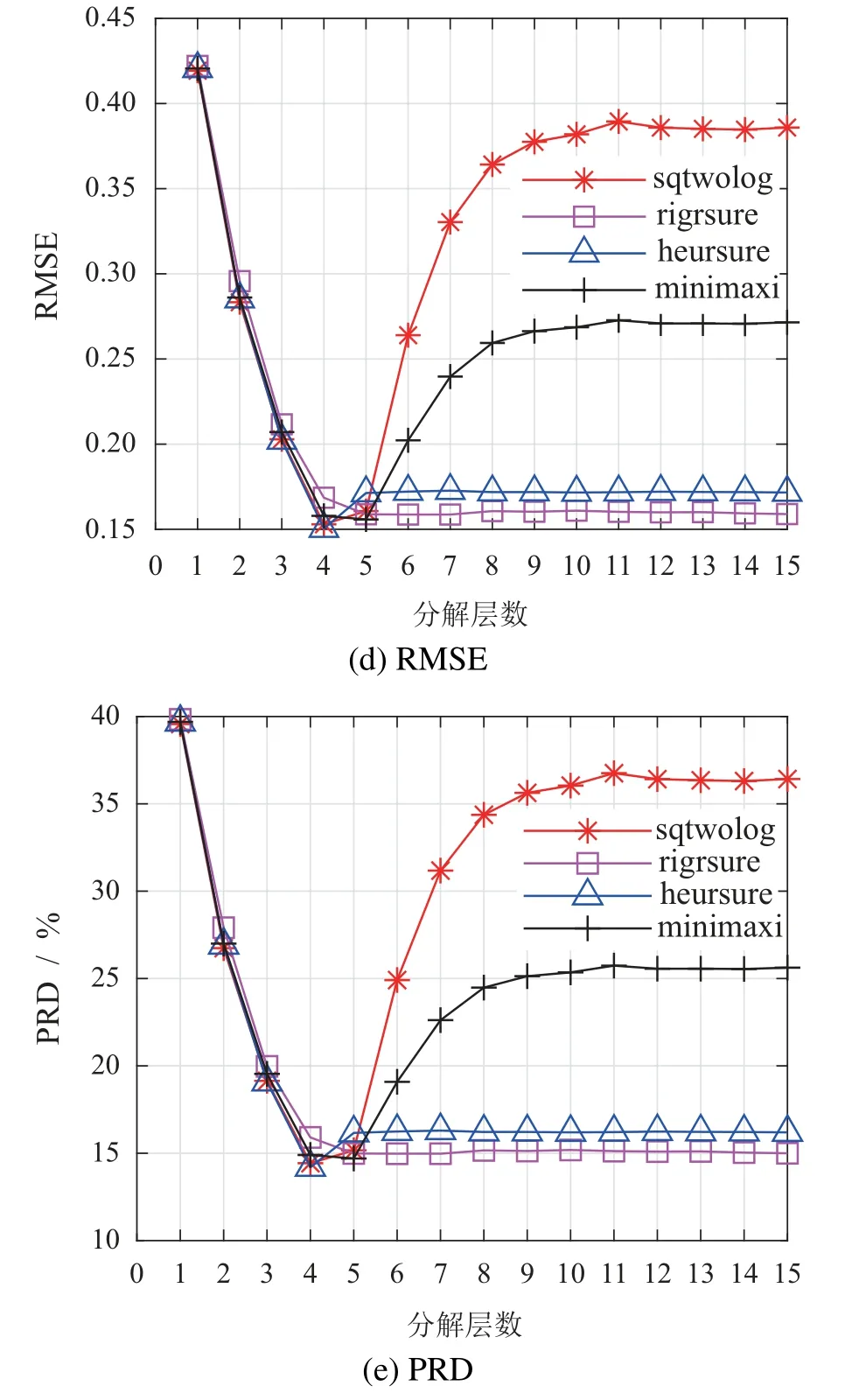
图4 采用不同分解层数消噪结果Fig.4 Denoised results based on different decomposition layers

3.3 CEEMDAN去噪过程

3.3.1 信号分解

为验证本文所提方法的有效性及优越性,分别用EMD,EEMD和CEEMDAN方法对仿真信号s1进行分析,得出IMF分量,之后计算每个IMF分量相关系数,通过设定阈值,选取相关系数值大的IMF分量进行信号重组,得到消噪后的信号.

图5为EMD,EEMD和CEEMDAN的信号分解结果,其中对于EEMD和CEEMDAN,在仿真信号中加入了100组标准偏差为0.2的高斯白噪声.

图5(a)表示通过EMD分解得到9个IMF分量和1个残余分量.其中分解得到的IMF分量中存在明显模态混叠现象.

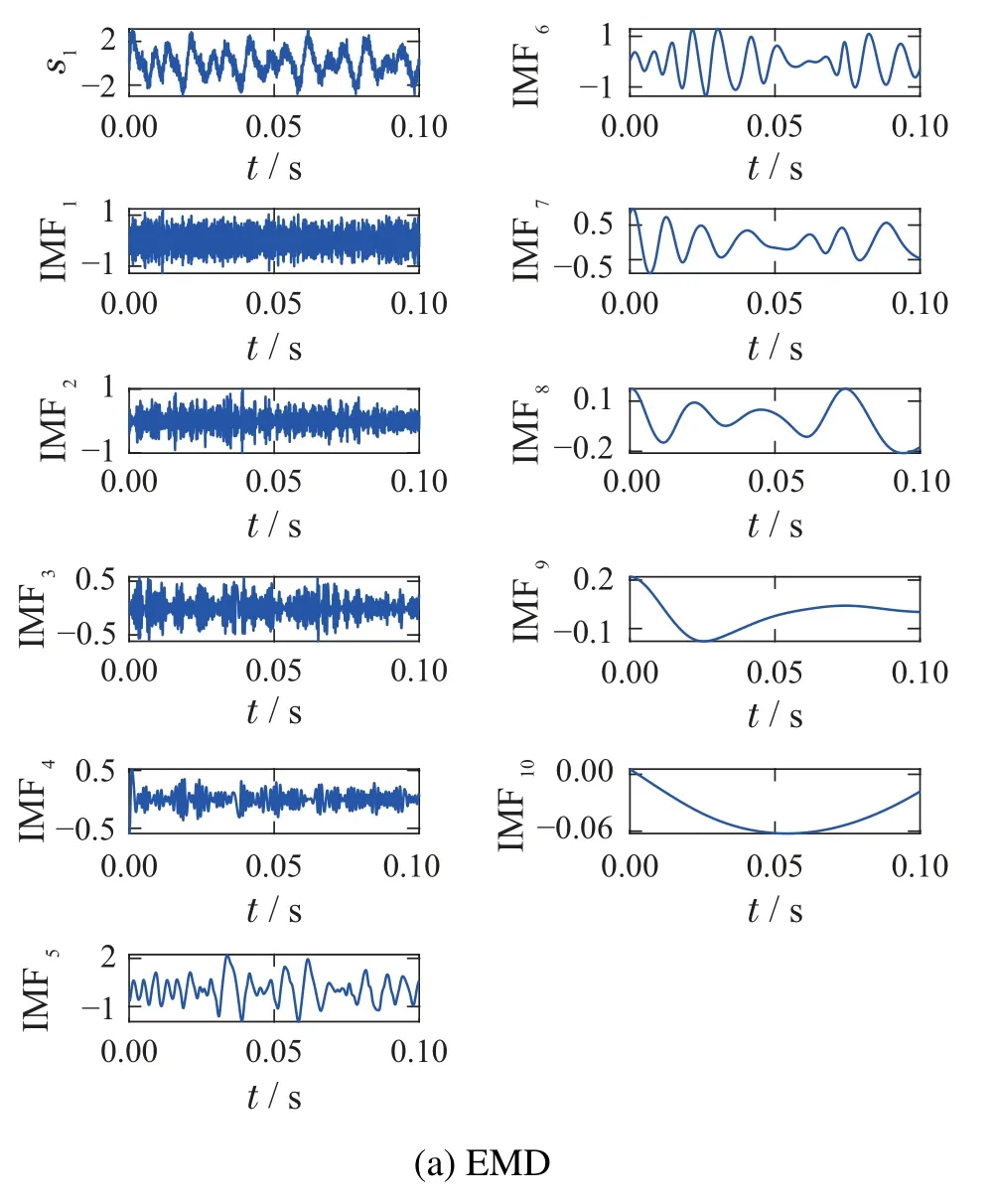
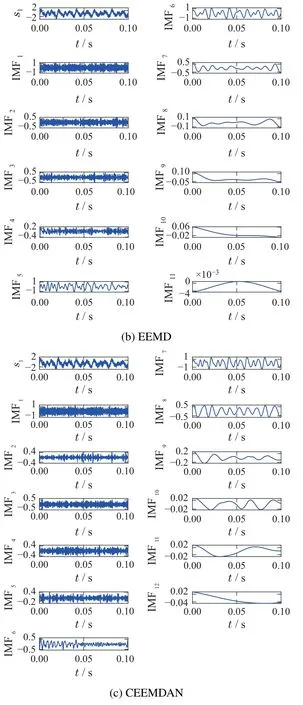
图5 仿真信号分解Fig.5 Decomposition of simulated signal

在图5(b)中,通过EEMD分解得到了10个IMF分量和1个残余分量.虽然EEMD在待分解信号中加入高斯白噪声并通过平均值消除加入的噪声,但是依然会存在模态混叠的现象.

图5(c)表明CEEMDAN分解出11个IMF分量和1个残余分量,与EMD和EEMD相比可以得到更多的振动信号信息.由于CEEMDAN分解在得到的第1阶IMF后进行总体平均计算,因此该方法能够有效地抑制模态混叠现象.

本文采用IMF的迭代次数箱式图来检测CEEMDAN分解的速度,箱式图结果如图6所示.

图6 IMF的迭代次数Fig.6 Iterations of IMF

图6表明,EEMD方法最大迭代次数为124,CEEMDAN方法最大迭代次数为83,CEEMDAN方法计算量明显低于EEMD,从而降低操作时间,提高信号分解的效率.

3.3.2 IMF分量选取

本节通过CC计算IMF分量的相关性,然后通过设置的阈值选取出有效的IMF分量.不同的IMF分量具有的CC值各不相同,经计算得出的阈值及选取结果如下表所示.

通过表1的选取结果,将提取出的有效IMF分量进行重构获取去噪信号.

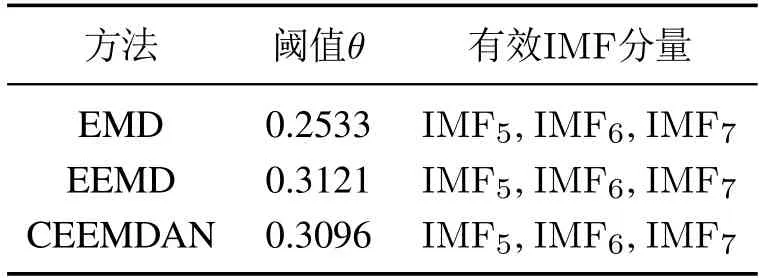
表1 阈值及选取结果Table 1 Threshold and selection results

3.4 不同方法消噪对比

不同消噪方法消噪后的去噪指标如表2所示.

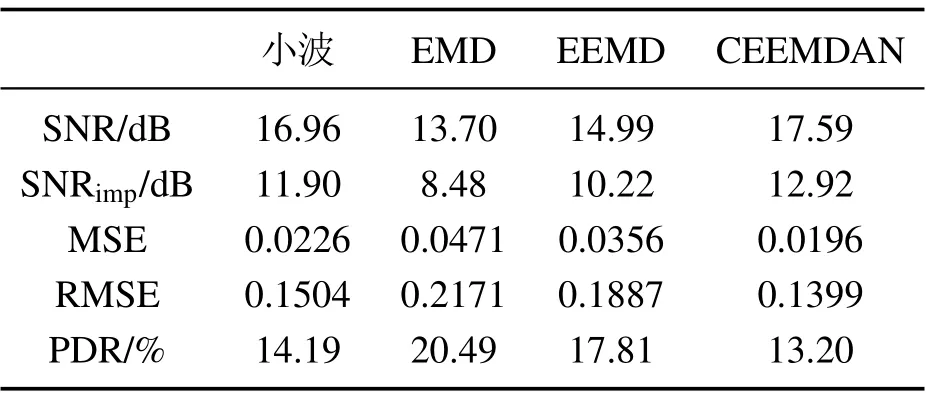
表2 不同方法去噪指标Table 2 Denoising index of different methods

由表2可知,小波去噪和CEEMDAN方法去噪的去噪指标均好于EMD和EEMD去噪.但是母小波和分解层次都需要人工选取,并且阈值选择不当会造成去噪信号发生畸变,会直接影响消噪效果.EMD和EEMD消噪后得到的信号与原始信号相差较大,由于存在的模态混叠现象不能实现良好的去噪效果,在去噪方面具有一定的局限性.而本文采用的CEEMDAN方法利用其自身优点对仿真信号进行分解,提取出有效的IMF分量进行重构,表2指标结果显示,CEEMDAN方法具有较高的SNR,SNRimp和较低的MSE,RMSE,PRD,验证了该方法在变压器振动信号消噪方面的有效性和优越性.

4 现场信号分析

本节利用CEEMDAN消噪方法用于变压器现场振动信号.本文采集的现场信号来自康巴什热电厂2号主变,型号为SFP10–420000/220,具体参数如表3所示.振动加速度传感器的灵敏度为100 mV/g,采样频率为10 kHz,分别对变压器A相、B相、C相进行振动信号采集,安装位置如图7所示,采集的振动信号如图8所示.

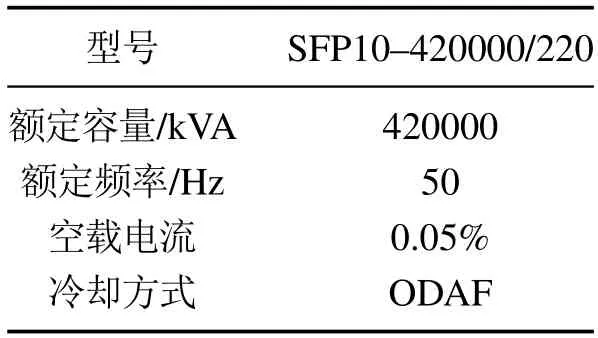
表3 变压器参数Table 3 Transformer parameters

图7 变压器及传感器位置Fig.7 Transformer and sensor position

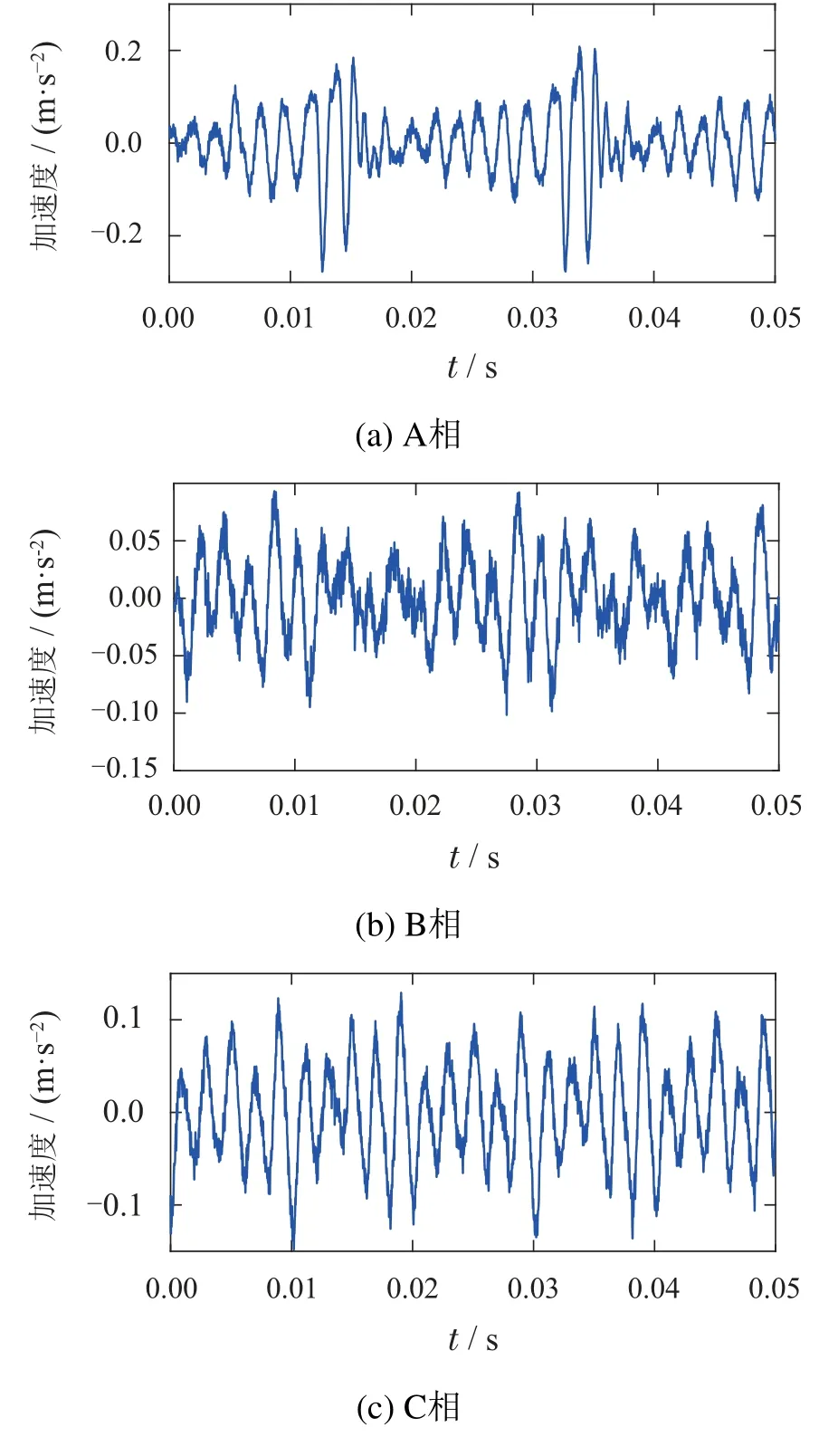
图8 变压器振动信号的加速度值Fig.8 Acceleration of transformer vibration signal

通过图8可以看出,现场的变压器振动信号存在一定的噪声,为得到有效的振动信号,本文采用CEEMDAN方法对A相、B相、C相振动信号进行分析,如图9所示.

由图9可以看出,3种工况下的振动信号,通过CEEMDAN分解均得到了11个IMF分量和1个残余分量.

图9 CEEMDAN分解Fig.9 Decomposition of CEEMDAN

对每个IMF分量计算CC值和阈值,并选出有效的IMF分量,选择结果如表4所示.

表4 阈值及选取结果Table 4 Threshold and selection results

通过对取出的有效IMF分量进行重构可以得到去噪信号,去噪信号如图10所示.

图10表明,经过CEEMDAN方法进行信号处理后,噪声在很大程度上得到抑制,证实了该算法的有效性.由于变压器现场振动信号与仿真信号不同,具有较强的不可知性,因此,本文将引入噪声抑制比(noise rejection ratio,NRR)来量化去噪效果[22].NRR计算公式如下所示:

图10 CEEMDAN去噪信号Fig.10 Denoised results by CEEMDAN

其中σ1和σ2分别为降噪前和降噪后的噪声偏差.该偏差值表示为

其中:Q为信号长度,Sd为第d个信号,µ为信号的均值.

本文将小波、EMD、EEMD去噪与CEEMDAN去噪做对比,4种方法去噪指标NRR见表5所示.

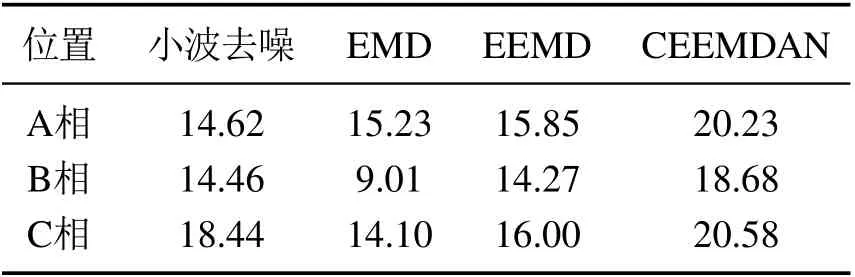
表5 不同方法的NRRTable 5 NRR of different methods

通过表5可以看出,对于不同方法的消噪结果,CEEMDAN具有更高的NRR,并且对于噪声成分较大的B相,其NRR达到18.68,远高于其他3种去噪方法.综上分析,通过CEEMDAN去噪结果表明该算法能够有效抑制振动号中混叠的白噪声,有效提取出在强背景噪声下的振动信号,与小波、EMD、EEMD去噪相比具有更好的消噪效果,适用于变压器振动信号的信息提取.

5 结论

本文提出了一种基于CEEMDAN的变压器振动信号去噪方法.论文采用CEEMDAN方法对变压器振动信号进行分解,然后通过CC及阈值对分解出的IMF分量进行提取,提取出有效的IMF分量并将其重构得到去噪后信号.通过仿真及现场信号分析得到结论如下:

1) 小波方法具有较高的时频分辨特性,但是母小波和分解层次都需要人工选取,阈值选择不当会直接影响消噪效果,在实际应用中具有较大局限性.

2) EMD和EEMD分解得到的IMF分量中总会存在模态混叠的现象,并且EEMD分解会残留一定的高斯白噪声,这会影响后续信号分析处理.而CEEMDAN方法能够分解出更为细致的信号分量,同时消除高频干扰和低频基线漂移,并且能够很好地消除模态混叠现象.

综上可得,本文提出的CEEMDAN方法能够在噪声环境下提取出有效的变压器振动信号信息,通过与小波、EMD、EEMD对比,CEEMDAN能够克服上述传统方法的不足,仿真和现场信号分析表明,所提方法能够有效提取出变压器振动信号,为变压器状态分析提供有力的分析工具.此外本文针对的是变压器单一的噪声类型.在实际的工程中,变压器可能会同时出现多种噪声混叠的现象.因此,未来的研究将集中于变压器振动信号的不同种噪声的去噪.考虑到不同的测量电路和传感器可能会导致不同的变压器振动信号,在未来需要提取来自不同测量条件的信号来验证该方法的有效性.