考虑充放电不平衡的风电功率平滑电池分组控制

张小莲,陈 冲,张仰飞,郝思鹏,孙啊传,武启川

(南京工程学院电力工程学院,江苏南京 211167)

1 引言

风电是常见的一种可再生能源发电形式,可独立并网或接入微电网、综合能源系统等,截止2020年末,我国风电并网装机容量已超282 GW,未来我国风电建设规模以及装机容量将继续扩大,然而风电的间歇性与波动性的特征也给电网稳定性和安全运行方面带来了巨大挑战[1–4].

为平滑风电功率波动,除了控制风电机组的运行状态,还可以采用电池储能系统(battery energy storage system,BESS)对风电功率进行吸收和补偿[5–6].BESS具有充放电速率快,额定容量大以及灵活可控等特点,因此利用BESS平滑风电功率是目前最常用的手段之一[7].采用单一BESS进行风电功率平滑已经比较成熟,但由于风电的不确定性带来频繁的充放电,以致充放电深度较浅,电池的利用效率低下,有损电池使用寿命[6,8].

因此,为了弥补单一BESS的缺陷,一些学者提出采取两组BESS或者电池分组控制,该项研究主要关注电池分组控制的充放电能量不平衡问题以及寿命衰减情况.文献[9]提出了采用双电池储能系统分别进行充放电,当达到特定条件时切换充放电状态的控制方式,并通过功率分配机制改善电池的寿命.文献[10]基于自适应高通滤波算法确定滤波时间常数,通过电池分组控制以缓解风电功率波动.文献[11]提出了两组电池的同步和异步控制策略以平滑其剧烈波动,验证了异步策略相比同步策略有更明显平滑效果.但上述文献聚焦分组控制策略设计和使用寿命的改善,并未考虑电池充放电不平衡问题.在电池分组控制中,保持电池组充放电平衡运行可有效避免电池组进入充电或者放电能力不足的极端情况.文献[6]根据不平衡状态实时调整双电池组的充放电,从而优化其平衡状态,但是该方法未讨论寿命衰减情况,而且采用分段平均算法计算并网目标功率,按不平衡状态修订并网目标功率时目标功率变化大,对电网冲击较大.文献[12]针对电池分组控制的不平衡问题提出了一种模糊控制策略,通过自适应调节一阶滤波平滑算法中的滤波时间常数以保持两组电池能量平衡,但该方法也未分析电池能量不平衡对其寿命产生的影响,而且面对剧烈风速波动时其改善效果较差.

本文基于一阶低通滤波平滑算法进行电池分组控制实现风电功率平滑,以电池组充放电能量不平衡度和寿命衰减程度为评价指标,分析寿命衰减与不平衡度的定量关系,并提出一种考虑不平衡状态的改进控制策略.根据电池组的不平衡度指标和各电池组的荷电状态(state of charge,SOC)动态修正滤波时间常数,有效提高电池组充放电深度和平衡状态.通过仿真和实验分析,对比传统控制策略、基于模糊控制的电池分组控制策略,验证了本文所提策略的平滑效果及其在不平衡度、寿命衰减方面的优越性.

2 电池分组控制运行原理与数学模型

本文采用图1所示的风储联合系统模型,风电场t时刻出力为Pw(t),两组锂电池组各自通过变流器与风电场并联,其t时刻发出功率分别为Pb1(t)和Pb2(t),Pg(t)则为风电场与储能装置的总输出功率,最终汇入交流电网.当Pb1(t)或Pb2(t)为正值时,表示电池组发出功率,反之则吸收功率.根据能量守恒原则,各功率之间的关系如式(1)所示[13]:

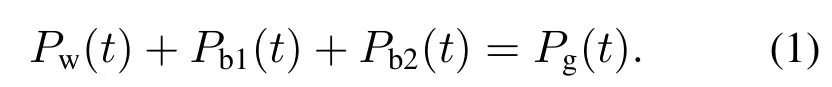
图1 基于电池分组控制的风储联合系统模型Fig.1 Wind-storage combined system model based on battery grouping control

将风电场电池分为两组进行控制,一组电池负责充电,另一组电池负责放电.当任意电池组达到其SOC限值,则两组电池立即交换充放电角色.如此配合运行,完成风电功率平滑任务,并保证同一时刻仅有一组电池工作.

按上述方式运行的两组电池的SOC 数学模型为[14]

式中:Ssoc1(t)和Ssoc2(t)分别为当前时刻的电池组1和电池组2的SOC值,µ1,µ2为电池组充电、放电角色标志.Pch(t),Pdisch(t)分别为当前时刻风电场所需的充电、放电功率,根据两电池组的角色赋值给Pb1(t)和Pb2(t).值得注意的是,需将Pch(t)取负值后赋值给执行充电任务的电池组.E1(t −1)和E2(t −1)分别为上一时刻的两电池组的剩余电量,∆t为采样周期,ηch和ηdisch为电池组的充电和放电效率,E1,E2为两电池组的额定容量.

例如,当电池组1承担充电任务,电池组2承担放电任务时,则µ1=1,µ2=0,Pb1(t)=−Pch(t),Pb2(t)=Pdisch(t);相反地,电池组1放电、电池组2充电时,则µ1=0,µ2=1,Pb1(t)=Pdisch(t),Pb2(t)=−Pch(t).

3 电池分组控制的不平衡状态及评价指标

3.1 电池分组控制的不平衡问题分析

采用电池分组控制吸收和补偿风电功率可平滑并网功率,但是分组运行过程中,当一组电池达到SOC上限或下限时,由于输出风电功率的急剧波动和不稳定性,另一组电池可能距离其SOC限值较远,导致两组电池充放电不平衡,甚至出现无法正常运行的极限情况,如图2(a),经过多次充放电切换,两电池组的SOC都过低,在第3次充放电切换后,两者SOC均已到达下限值,无法补偿风电功率缺额,影响平滑效果,图2(b)所示的充电能力不足与上述情况类似,而且长期运行下去将对电池组寿命造成不利影响.

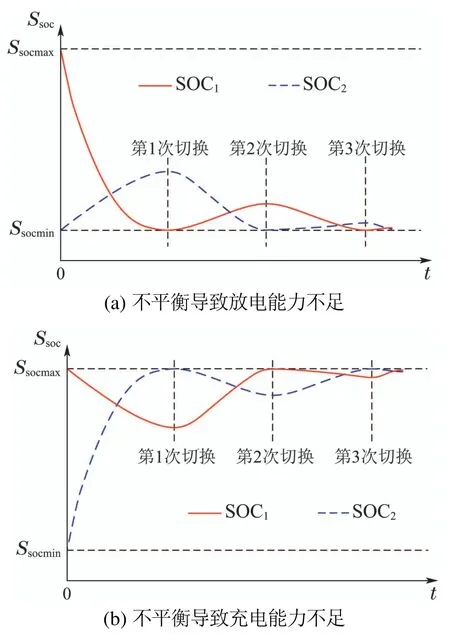
图2 充放电不平衡导致充放电能力不足的极端情况Fig.2 The extreme conditions of insufficient charge and discharge capacity due to unbalanced charging and discharging

3.2 不平衡状态评价指标

1) 充放电能量不平衡度指标.

为了评估电池分组运行过程中的平衡状态,引入不平衡度指标A(t),其定义为[6]

A(t)越接近0表明两组电池的平衡程度越高,当两组电池容量相同时,可充电量大致等于可放电量;当A(t)小于0时,表示两组电池中可充电量大于可放电量,反之A(t)大于0意味着可放电量大于可充电量;采用A(t)的绝对值|A(t)|表示两组电池的绝对不平衡度,|A(t)|值越大,两组电池不平衡程度越高.

2) 寿命衰减指标.

将充放电深度∆Ssoc偏离∆Ssocb的程度作为电池寿命衰减的评价指标,其表达式为[15]

式中:∆Ssocb称为标准充放电深度,是电池寿命周期内吞吐能量最大值对应的充放电深度,代表寿命衰减程度最低,是一种最优的运行状态[15].本文根据文献[16–17]将其设为0.8.ε值越大,则电池在寿命周期内所能吞吐的电量越小,表明寿命衰减越严重.定义ε1和ε2分别为两电池组的寿命衰减指标.

将电池运行的SOC上下限值分别设置为:Ssocmax=(1+∆Ssocb)/2和Ssocmin=(1−∆Ssocb)/2,以此可实现电池组SOC处于[Ssocmax,Ssocmin]内以∆Ssocb进行全充全放时吞吐出最大能量,将电池寿命衰减降到最低[15].

3) 寿命衰减指标与不平衡度指标的关系.

讨论两个充放电阶段的SOC,|A(t)|以及ε.令β=ε1+ε2,设本次充放电阶段结束时刻电池组1和电池组2的SOC分别为Ssoc1和Ssoc2,绝对不平衡度为|A|,上一充放电阶段结束时刻两电池组的SOC分别为绝对不平衡度为|A′|,并假定本阶段电池组1执行放电任务,电池组2执行充电任务.

根据式(3)–(4),本阶段结束时刻,两组电池的β和绝对不平衡度|A|分别为

相应地,上一阶段结束时刻两组电池的绝对不平衡度|A′|为

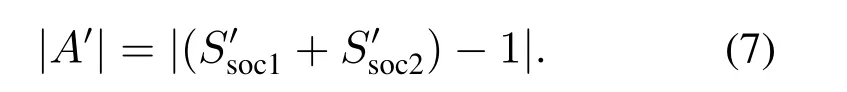
假设本阶段为电池组1先达到切换条件,上一阶段也为电池组1先达到切换条件,则

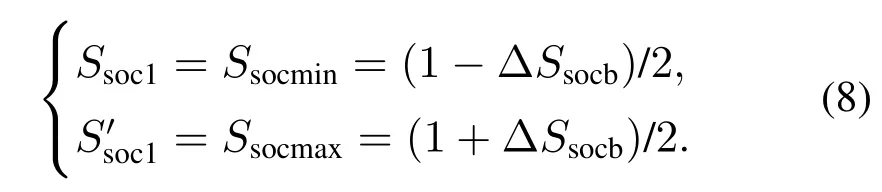
将式(8)带入式(5)–(7),可得

通过分析得出所有可能的切换条件下,每个充放电阶段结束时刻,|A|与β都有式(9)的关系.

通过上述分析可知,若|A(t)|较大,说明其中一组电池的SOC距离限值(Ssocmax或Ssocmin)较远,此时充放电深度较浅,即ε值较大,使电池在寿命周期内吞吐的电量变少,加剧了寿命衰减.因此,保证较小的充放电能量不平衡度,不仅可避免图2所示的充放电能力不足的状况,可同时获得良好的充放电深度,延长电池使用寿命.

4 改进策略

4.1 基于低通滤波的风电功率平滑算法

风电功率平滑常通过一阶低通滤波器对原始风电功率进行滤波,得到风电场的并网目标功率,一阶低通滤波器的传递函数为

其中T为滤波时间常数.

根据上式,随着输入信号频率升高,输出信号的幅值减小,说明该滤波器对高频信号起到衰减的作用.其中截止频率fc=1/2πT,当T增大时,fc减小,滤波器阻带变宽,输出信号高频分量减少,输出波形更加平滑,且1 Hz以上的风电功率含量较少,可忽略不计,而0.01～1 Hz频段的功率波动较大,且亟待平滑的风电功率波动主要集中在此频段[18].

Pw经滤波后输出的功率为并网目标功率Pg_ref.当Pg_ref(t)>Pw(t)时,为补充缺额的并网功率,电池组进行放电,t时刻的充放电功率分别为

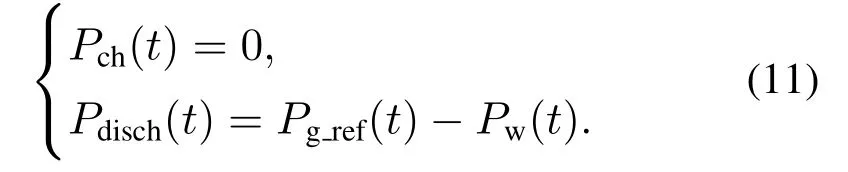
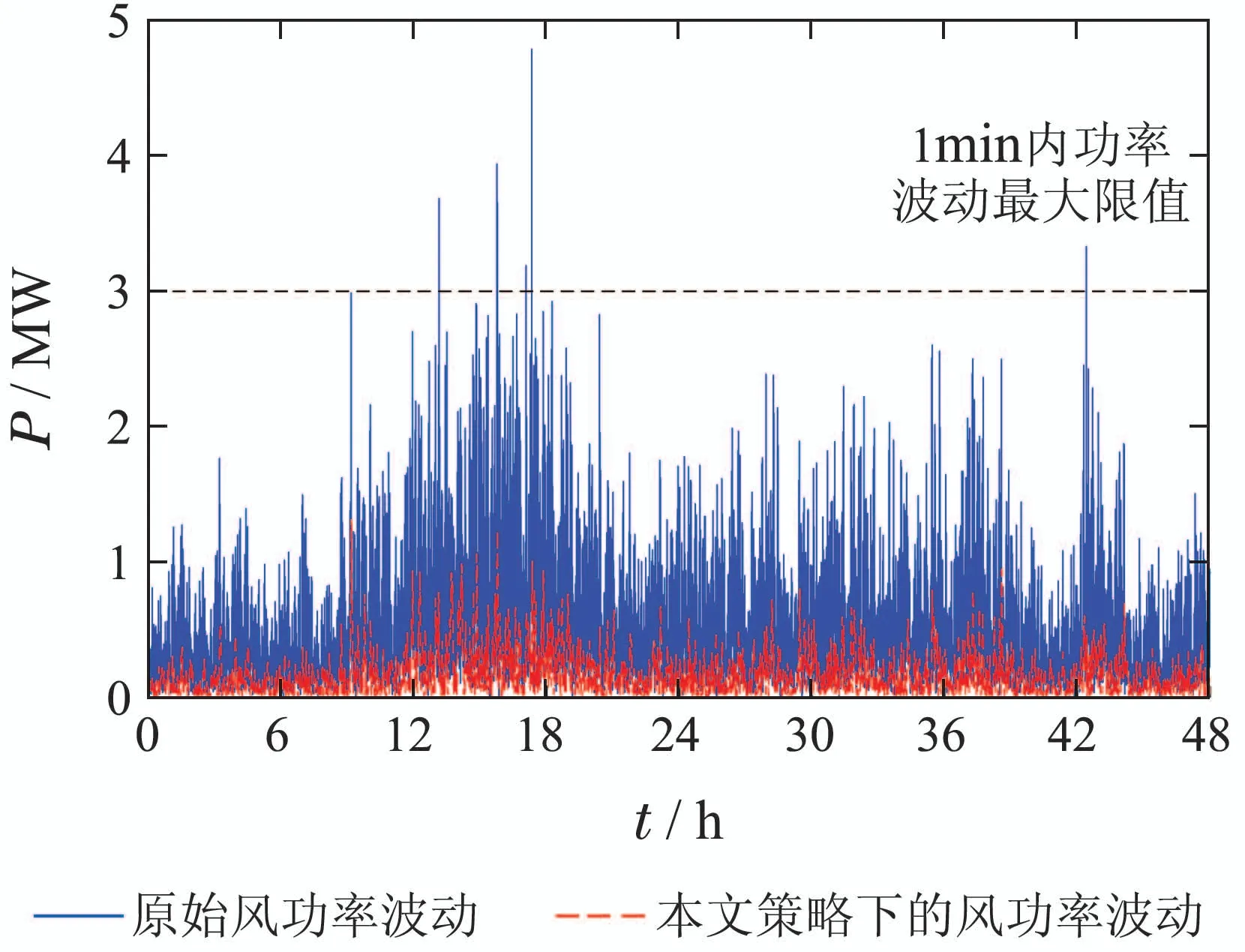
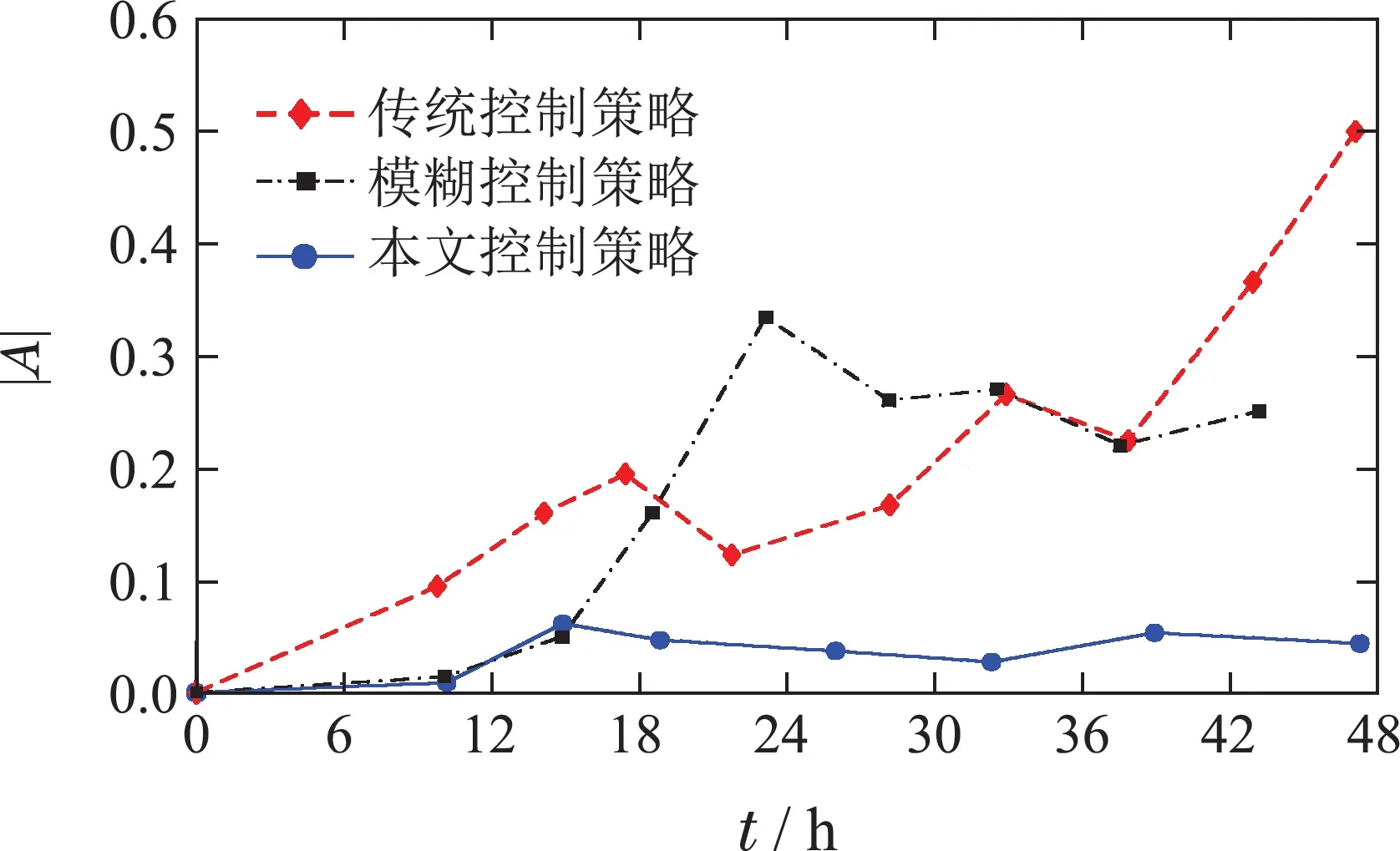
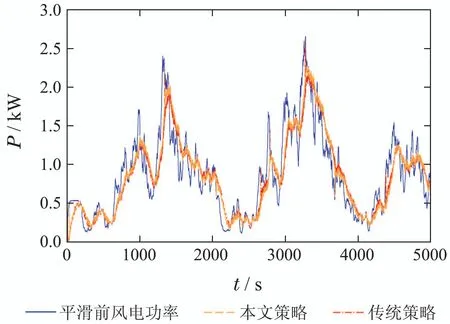
若Pg_ref(t)

为评价风电功率的平滑效果,引入文献[19]的波动谐波含量(the fluctuation harmonic content,FHC)指标,其定义如下:

式(13)中:F为选取的某频率段,P(f)为F频段内的频率f下的功率幅值,P0为功率的直流分量.FHC越小,表明在F频段内功率波动分量越少,输出功率越平滑.

4.2 考虑不平衡状态的改进控制策略

两组电池充放电不平衡会给电池带来严重的寿命衰减,为改善电池分组控制的充放电不平衡状态,本文将根据不平衡度指标和荷电状态实时调节滤波器的时间常数,从而间接维持|A(t)|在较小的数值.

根据电池分组运行状态,分为以下4种模式:

a)A(t)>0且电池组执行充电任务.

此时两组电池SOC均接近上限,可放电量大于可充电量,执行充电任务的电池组应降低充电功率,通过适当减小滤波时间常数T,可降低处于充电状态电池组的SOC的上升幅度,且SOC越大代表充电电池组可充电量越少,则应继续减小T.

b)A(t)>0且电池组执行放电任务.

此时应适当增大T,从而提高电池的放电功率,加速放电电池组SOC降落,且SOC越大,电池可放电量越多,应使T更大.

c)A(t)<0且电池组执行充电任务.

此时两组电池SOC均接近下限,充电量大于可放电量,通过增大滤波时间常数T可提高充电电池的充电量.且SOC越小,说明充电电池可充电量越多,则T的取值应更大,以达到SOC加速上升的目的.

d)A(t)<0且电池组执行放电任务.

此时应适当减小T,降低放电功率,延缓SOC下降,且放电电池SOC越小,T应越小.

根据上述模式调整滤波器时间常数T,将促使两组电池SOC尽量对称,从而使A(t)维持在0附近.

滤波时间常数T按式(14)设置

其中:T0为基础时间常数,α(t)·∆T为滤波时间常数修正项,α(t)为修正系数,∆T为调节步长.本策略通过实时改变α的大小来调节滤波时间常数,根据上述分析,具体调节规则如下:

αch(t)和αdisch(t)分别为两组电池当前充电和放电时刻的修正系数,由于充电和放电不可能同时进行,因此α值也随着两组电池充电和放电状态的切换而变化.将式(15)–(16)合并,可得

式中:Ssoc(t −1)为上一时刻的荷电状态,fch,disch和fA为区分4种模式的标志变量,fch,disch,ne和fA,ne分别为fch,disch和fA的取反数,例如,fch,disch取1 时,则fch,disch,ne取0.fch,disch表示电池组为平滑风电功率需要进行充电或放电,fA代表当前A(t)的状态,其设定如表1所示.

表1 电池组状态规则表Table 1 The state rule of the battery

改进策略的控制流程图如下图所示,风储联合系统工作过程中,根据两组电池的SOC和A的反馈,在到达平滑任务结束时刻tend前,通过式(17)实时调节系数α以达到修正时间常数T的目的,可使|A(t)|保持较小的值,从而改善电池充放电不平衡的问题.

图3 改进策略流程图Fig.3 Flowchart of the improved strategy

所提改进控制策略在调整滤波时间常数时,不仅能够依据不平衡度A进行调整,还以SOC状态、SOC上下限值为基础,可以很好地兼顾不同SOC状态对时间常数的需求,从而更迅速地减小不平衡度.

5 仿真分析与实验平台验证

5.1 仿真分析

本文采用某风电场2 天的实测风速,通过MATLAB/Simulink搭建仿真模型,得出传统控制策略、文献[12]的模糊控制和本文改进控制策略3种策略下电池分组运行时的风电场并网功率、电池组SOC变化曲线,并分析风电功率平滑效果、电池组的不平衡度、β值和充放电深度,以验证改进策略的有效性及优势.

1) 仿真参数.

主要仿真参数如表2所示.将储能系统分为相同额定容量的两组电池.文献[7]指出储能容量数值上不超过风电场总装机容量的25%,本文算例中配置单组电池的容量为3 MW·h,容量配置合理.电池组1和电池组2的初始SOC分别为0.9和0.1,电池组初始任务分配为电池组1负责放电,电池组2负责充电.传统控制策略采用滤波时间常数恒定的电池分组控制,其滤波时间常数T=240 s.

表2 主要仿真参数Table 2 Main simulation parameters

2) 风电功率平滑分析.

针对2天时长的实测风速,分别采用传统控制策略、模糊控制策略和本文改进控制策略方式,可得出并网后得风电功率波形,仿真结果如图4所示.可知,通过3种平滑策略,都可有效地平滑风电功率,如24～26 h的局部放大图,原风电功率经过平滑后可得到较为平坦的功率曲线.

图4 平滑前后的风电场输出功率Fig.4 Wind farm output power before and after smoothing

分别计算原始风电功率以及3种策略平滑后0.01～1 Hz频段的FHC值,结果如表3所示.

由表3可知,3种控制策略下的风电功率FHC在需要重点平滑的0.01～1 Hz频段平滑效果很明显.本文改进控制策略与其他两种策略具有基本同等的平滑效果,相比未平滑的风电功率,频率波动减少约70%.

表3 几种控制策略下的风电功率FHC值Table 3 FHC value of wind power under several control strategies

《风电场接入电力系统技术规定》对风电并网的功率作出了如表4所示的相关标准[20].

表4 风电场最大功率波动限值规定Table 4 Regulations on maximum power fluctuation limit of wind farm

针对本文策略,经仿真得到平滑前后的风电功率分别在1 min和10 min内的最大波动,10 min内的最大波动功率值全部符合国标,而对于1 min内的功率差值如下图所示,平滑前的功率在部分时段显然超过了国标规定的3 MW最大限值,并有较多时段非常靠近最大限值,经本文策略平滑后的风电功率差值都降低到1.5 MW以下,符合国标技术规定,从而验证了该策略对风电功率平滑的有效性.

图5 1 min内风电场最大输出功率波动Fig.5 Maximum output power fluctuation of wind farm within 1 minute

3) 电池组的SOC曲线分析.

对3种策略进行仿真,分别得到图6所示不同控制策略下的SOC变化情况.

图6 不同控制策略下的SOCFig.6 SOC of different strategies

由图6可知,传统策略下两组电池的充放电深度总体上较浅,特别在12～18 h,此时风电功率波动较为剧烈,电池组需要吸收或补偿的功率较大,导致两组电池的SOC极度不平衡,且在24 h以后,不平衡程度逐渐恶化;而模糊控制策略下两组电池前18 h的不平衡状态较传统策略好,但18 h以后不平衡情况较严重;相比上述两种策略,改进策略很好地改善了电池组的不平衡状态,特别是在18～48 h明显改善了两组电池的不平衡情况,该策略随SOC的变化实时修正滤波时间常数T,如图7所示.

图7 改进策略的滤波时间常数TFig.7 The filtering time constant T of the improved method

由于充放电深度的改善,改进策略减少了电池充放电切换的次数,相较于传统策略的切换9次减少到7次,避免了两组电池频繁切换充放电状态,对电池的使用寿命有一定改善.

4) 不平衡度和寿命衰减指标分析.

采用第3.2节的不平衡度|A|和寿命衰减指标β对仿真结果进行分析.通过仿真可得不同控制策略的绝对不平衡度|A|和寿命衰减指标β,结果如图8–9所示.

图8 绝对不平衡度|A|Fig.8 Absolute imbalance degree|A|

分析图8和图9可获得以下结果:

图9 寿命衰减指标βFig.9 The index of decline in cycle life β

a) 改进策略具有更小的|A|.相较于传统控制和模糊控制,改进策略下两组电池绝对不平衡度较小,即使在风电功率波动较剧烈的12～18 h时段,|A|波动也较小,表明本文策略下的两组电池尽可能维持在充放电平衡状态.

b) 改进策略具有更小的β.传统控制策略和模糊控制策略下两组电池的β从风电功率波动较大的12 h时刻开始急剧恶化,且总体上的β值偏移程度大,在改进策略下,电池组的β基本维持在较低水平,验证了改进策略的优势.

c) 改进策略可充分利用电池组容量,延缓了充放电切换时刻.由图8可知,改进策略第7次充放电切换发生在48 h左右,而其他两种策略均发生在38 h左右.采用改进策略时每次充放电切换时刻相对传统策略都会延迟,说明充放电深度得到优化使每个充放电阶段都能吞吐更多电量,有利于延长其使用寿命.

5.2 基于风–储实验平台的验证

构建了包含风机模拟器、磷酸铁锂电池、电池并网系统、PLC、上位机等硬件的风–储实验平台,关键设备如图10所示.其中,风机模拟器由一台额定功率18.5 kW的异步电动机和一台额定功率为15 kW的永磁同步发电机组成,异步电动机模拟风力机的气动特性,拖动发电机工作,发电机通过变流器并网运行.两组磷酸铁锂电池分别通过DC/DC、DC/AC两级变流器并入交流电网运行.基于Beckhoff PLC实现改进策略,控制风力机和锂电池组运行,验证改进策略的有效性和优越性.

图10 风–储实验平台Fig.10 Experimental platform of wind-storage combined system

分别采用本文改进策略和传统策略运行5000 s,两种策略下风–储系统的并网功率如图11所示.

图11 平滑前后的风机输出功率Fig.11 Wind turbine output power before and after smoothing

经计算,平滑前后风电功率0.01～1 Hz频段的FHC如表5所示,相较于平滑前,传统策略的FHC降低了61.7%,本文策略的FHC降低了63.5%,能够有效地平滑实际运行中的风电功率波动.

表5 实验下的风电功率FHC值Table 5 FHC value of wind power under the experiment

两种策略下电池组的SOC如图12所示.为了缩减实验时间,期望在短时间内完成多次充放电切换,将SOC上下限值分别按比例缩放为0.55和0.45.

图12 实验平台的SOCFig.12 SOC of the experiment platform

由图12可知,传统策略下电池组的可充电量越来越少,且充电能力不足的情况愈发严重,电池组充放电极度不平衡;本文策略下的电池组充放电则保持在平衡的状态,基本达到“全充全放”的目标.

计算获得该实验下两组电池的绝对不平衡度|A|和寿命衰减指标β,如图13和图14所示.

由图13和图14可知,传统策略下在第1,3次电池充放电切换时绝对不平衡度过大,两组电池充电能力极弱,且寿命衰减程度一直处于递增趋势,对电池寿命伤害较大;而本文策略下的|A|和β相对平稳,保持在0附近,相比传统策略,电池组的|A|平均值提升93%,β平均值提升95%,在实际运行中两组电池寿命衰减较小,运行状态得到优化.

图13 实验下的绝对不平衡度|A|Fig.13 Absolute imbalance degree|A|under the experiment

图14 实验下的寿命衰减指标βFig.14 The index of decline in cycle life β under the experiment

6 结论

采用电池分组控制进行风电功率平滑时,为有效改善电池组充放电不平衡状态,优化电池组使用寿命,本文分析了电池组不平衡状态与寿命衰减指标之间的关系,并提出改进策略对电池组的SOC进行优化.

主要结论有:

1) 电池组的寿命衰减指标与不平衡度呈线性关系,若电池分组运行过程中电池组之间始终保持较小的不平衡度,可有效延缓其寿命衰减;

2) 本文所提策略能够很好地兼顾电池组不平衡度以及SOC状态,在改善不平衡度方面具有明显优势.经实验验证,不平衡度和寿命衰减指标可提升90%以上;

3) 改进策略在优化不平衡度指标的同时获得了更好的充放电深度,相较传统策略和模糊控制策略,可显著降低电池组充放电切换频率,有利于电池组健康运行;

4) 滤波时间常数是决定平滑效果和储能系统运行状态的重要参数,在满足风电并网的平滑要求的前提下,可通过该参数的优化充分实现储能系统SOC状态优化以及容量配置优化等.

本文储能系统的容量是根据其他学者总结得出的一般性结论设置的,未统筹各种指标(如经济性、平滑效果、运行优化等)进行配置.在未来的研究中,以期使用容量更小的电池组实现该策略,在保证平滑效果、良好不平衡度和使用寿命的前提下降低容量配置.