瞬变电磁视时间常数tau成像分析与应用研究

刘 冲， 王宇航， 皇 健，罗 勇

(1.成都理工大学 地球物理学院， 成都 610059；2.四川省地震局，成都 610041)

0 引言

目前瞬变电磁成像与反演发展较慢，基本局限于一维成像和反演，而反演速度较慢，严重制约了电磁数据的分析处理，因此力求探索一种快速的、高效的电磁数据处理方法，甚至通过处理现场测量数据来迅速了解测区地质异常体的大体分布规律，或为后续反演提供约束参数。需要探索地质体岩性参数与电磁响应之间的关系，充分利用这一物理规律来达到寻找异常体。静恩杰、李志聃[1-2]通过分析矿体内的感应电流，应用电路理论解释瞬变电磁场的物理过程，得出了矿体时间常数tau与导电性的关系，指出导电性差的矿体，其时间常数值较小；导电性良好的矿体，其时间常数值较大，并给出了一般良导体时间常数的表达式τ=KAσμ和几种规则异常体的时间常数表达式；静恩杰等和牛之琏[2-3]分析了电磁响应与时间常数的关系，并导出了在瞬变场衰减晚期的关系式A(t)=A0e-(t/τ)。Jiuping Chen等[4]探讨了瞬变电磁时间常数的估算，并应用矩阵束在tau域中对大地电磁数据进行了特征参数提取与重构；J.Sott Holladay等[5]对局部异常体的时间常数进行了预测估计，通过时间常数tau来分析异常体；牛之琏[3]提出了任意局部导体的晚期瞬变电磁响应与时间常数的关系表达式V(t)∝e-(t/τ)/τ，指出时间常数tau与异常体岩性参数和物性参数有关。以上所有的分析研究仅局限于瞬变电磁一维展开，并将晚期按统一的时间常数tau来衰减。作者基于以上理论，通过分析时间常数与电磁响应的规律，得出视时间常数tau值成像，在剖面和时间(水平)切片上对时间常数进行了分析，为圈定地质异常体提供了有效的方法，并为瞬变电磁反演约束参数的限定提供了依据。

1 时间常数tau的理论基础

1.1 tau的物理意义

一次磁场在周围传播过程中，如遇到地下良导电的地质体，将在其内部激发产生感应电流，又称涡流或二次电流。二次电流随时间变化，因而在其周围又产生新的磁场，称为二次磁场。由于良导电矿体内感应电流的热耗损，二次场大致按指数规律随时间衰减。二次场主要来源于良导电体的感应电流，因此它包含着与矿体有关的地质信息。根据二次场的衰减规律进行分析处理，可以解释地下矿体及相关物理参数。

据法拉第电磁感应定律，当发射电流突然关断时，地下良导体将产生感应电流，感应电流在地下矿体内扩散过程可分为三个阶段[1]，为了维持矿体内原磁场，在断电初期，感应电流集中分布于矿体表面形成表面电流，该阶段称为早期时间；随着感应电流在矿体内的热损耗，表面电流开始向矿体内部扩散，其扩散速度一般与矿体的导电滤波成反比关系，称中期阶段；当矿体内感应电流扩散经过一段时间后便进入所谓的晚期阶段，其感应电流的每个线电流的阻抗和感抗均趋于渐近值，是晚期阶段主要特征，此时矿体内电流分布趋于相对稳定，热耗损速度减慢，表现为与感应电流相对应的二次场衰减速度减缓。

矿体内感应电流及与之对应的二次场随时间变化率，取决于矿体的岩性和物性参数(如电导率、磁导率、矿体尺寸大小及形状等)。早期矿体表面电流的分布仅与矿体的形状和大小有关，而与矿体的电导率几乎无关。

瞬变电磁曲线变化速率的大小，取决于异常体的电性好坏和几何形状，其电性和几何形状反应在它的时间常数上，因此，异常体的时间常数决定瞬变长衰减速率的大小，是确定异常体电性好坏的重要参数。几何形状相同的矿体，导电性越好，其时间常数越大，一般导体的时间常数可表示为[2]：

τ=KAσμ

(1)

式中K为随异常体而变的常至数；A为与异常体几何形状有关的参数；σ为为电导率，μ为磁异常，也可用μ0近似代替(单位ms)。

1.2 tau与地质异常体的瞬变电磁响应关系分析

根据以上分析，对于球体导体中感应涡流进入晚期后，涡流分布状况已处于稳定，并且按指数规律衰减。这种结论也适合于其他形状的有限导电体。那么就有可能用(图1)一个包含有等效电感L和等效电阻R的单匝电流环来等效这种晚期涡流。两者的外场具有相似的规律[3,6]。

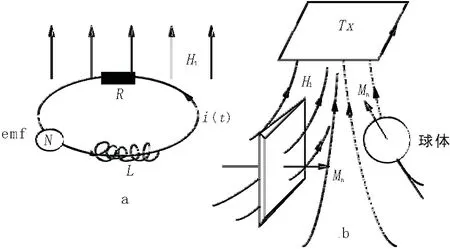
图1 有限导体的等效电路[3]Fig．1 The equivalent circuit of the conductor(a)有限导体的等效回路示意图；(b)板状体和球体的Mn方向示意

设：φ1为等效回路切割一次场的磁通量；切断时间为tof；在切断时间内，等效回路中产生的感应电动势为φ1/tof；感应偶极矩为Mn；激励场的法向分量为H1n。

利用等效回路的瞬态方程[3]：

(2)

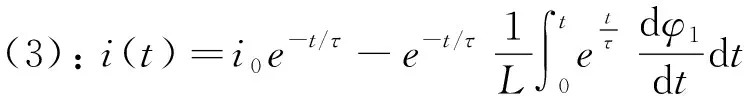
(3)

在供电时间内(t<0)，回路中没有感应电流产生，在H1切断的时间tof内，感应电流由一次场通量变化率确定。切断一次场后(t>tof)，公式(2)可变为式(4)。

(4)

等效回路中感应电流为：

(5)

据电磁感应定律：

得到一次场脉冲间歇时间(t≥tof)感测到的感应电压：

V(t)=-A0/tof(etof/τ-1)e-t/τ

(6)

在tof≤τ的情况下：

V(t)=A0/τe-t/τ

(7)

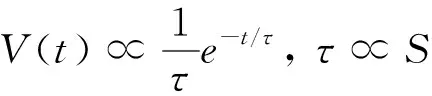
式中：I1发送电流；tof为关断时间。

Holladay和Chen[4]提出对于一个独立的目标体的瞬变电磁响应，其测量磁场B和感应电压V可以分解为单个极性响应的加权总和。

(8)

(9)

V(t) =AeffdB/dt

(10)

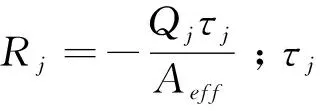
(11)

由式(7)、式(9)和式(11)可以看出，局部导电体上瞬变电磁响应的异常幅度及衰减速度，很大程度上决定于导体的时间常数τ。

对于不同导电性地质异常体而言，其时间常数tau值较小，尽管二次场初值较大，但其衰减速度较快(如图2中测点b所示)；反之，导电性良好矿体，时间常数tau值较大，尽管二次场初值较小，但衰减速度慢(如图2中测点a、c所示)。而一般导电性矿体典型的衰减时间范围从100 μs～200 μs至10 ms～20 ms[3]。

图2 瞬变电磁场衰减规律与时间常数tau的关系图Fig．2 Diagram for the relation between transient electromagnetic field attenuation andtime constant tau

对于式(7)、式(9)和式(11)所表示的是单一地质异常体的瞬变电磁响应与时间常数tau的关系，即时间常数tau是唯一的。在地下不同深度，相对于复杂的地质构造，其时间常数tau是变化的，所以式(7)、式(9)和式(11)中的tau值在不同时间点是不相同的，即对应不同深度反映的时间常数tau应不相同。而式(7)、式(9)和式(11)中，在瞬变电磁进入晚期时才有此规律，所以在瞬变电磁晚期分时窗进行时间常数求取，得到晚期不同时间点，即不同深度处的时间常数，以得出在晚期对应深度上的异常体分布规律。由于良导电性异常体的响应有延迟效应，晚期道时间常数不但有时间窗内异常地反映，同时还包含了部分早期良导电性矿体响应信息，因此时间常数是一个地下测区所有矿体的综合响应。但瞬变电磁在晚期道信号弱，并且易受干扰，当信噪比较差时，出现了衰减负值时，该方法即失效。

针对于不同的地质异常体(二度体或三度体)可应用公式(7)、式(9)和式(11)得出各时间点的时间常数，然而电磁响应是体积效应，提取各时间窗(t1,t2)内的时间常数τ，对应的不是单个时间点的时间常数，而是对应该时窗内异常体衰减系数的综合反映，因此可以称为视时间常数。其反应的主要特征为这一时间窗内对应的所有地质异常体的响应。

2 时间常数tau的应用

2.1 薄板模型数值模拟试算

根据以上理论，建立模型如图3所示，为一薄板模型，测区为 1 000 m×300 m，模型埋深为100 m，长宽E-N为200 m×200 m，薄板中心位置为EN(10 400，10 200)，电导为10 S，其背景层为空气层，共4条测线平行排列，从左至右依次编号为测线1、测线2、测线3、测线4，测线长为 1 000 m，测线间距100 m，测线1与薄板异常体边缘的水平间距为100 m，测线2、测线3位于异常体边缘正上方，测线3横穿异常体中心。该模型所采用的数值模拟方法为Maxwell软件中内置的全空间薄板正演模块。

图3 薄板正演模型Fig．3 Thin sheet model

通过正演模拟和tau值求取，得到如图4所示的视时间常数tau值剖面图，从图4中可以看出，薄板的横向(测线方向E)最大异常宽度在300m左右，与薄板的实际E向长度相差100 m。这是由于低阻异常体对电磁场有吸附作用，导致薄板附近较远距离处的测点都受到低阻薄板的影响，由于电磁场体积效应，使得视时间常数是测点附近所有异常体的综合响应，图4中视时间常数是针对晚期时间道做的，所以薄板的垂向(深度方向)并没有很好地反映出来。当测线向薄板异常体边缘靠近时，视时间常数tau异常范围逐渐变窄(如图5所示)，边缘处时间常数tau值异常宽度在200 m左右，与薄板异常体宽度吻合良好；当测线远离异常体时，时间常数tau的畸变趋于微弱，接近平稳，即受薄板异常影响微弱。图6为图5在时间t=1.9 ms的水平切片图，从图6中可以直观地看出时间常数tau在晚期道水平切片上的变化规律，即薄板中心处时间常数tau最大，远离薄板，时间常数tau值逐渐减小，其时间常数tau异常区在平面的展布与薄板相似。从图6表示的晚期时间常数tau的水平切片图，能很好地反应晚期时间道(即深部)地质体在水平空间上的分布。

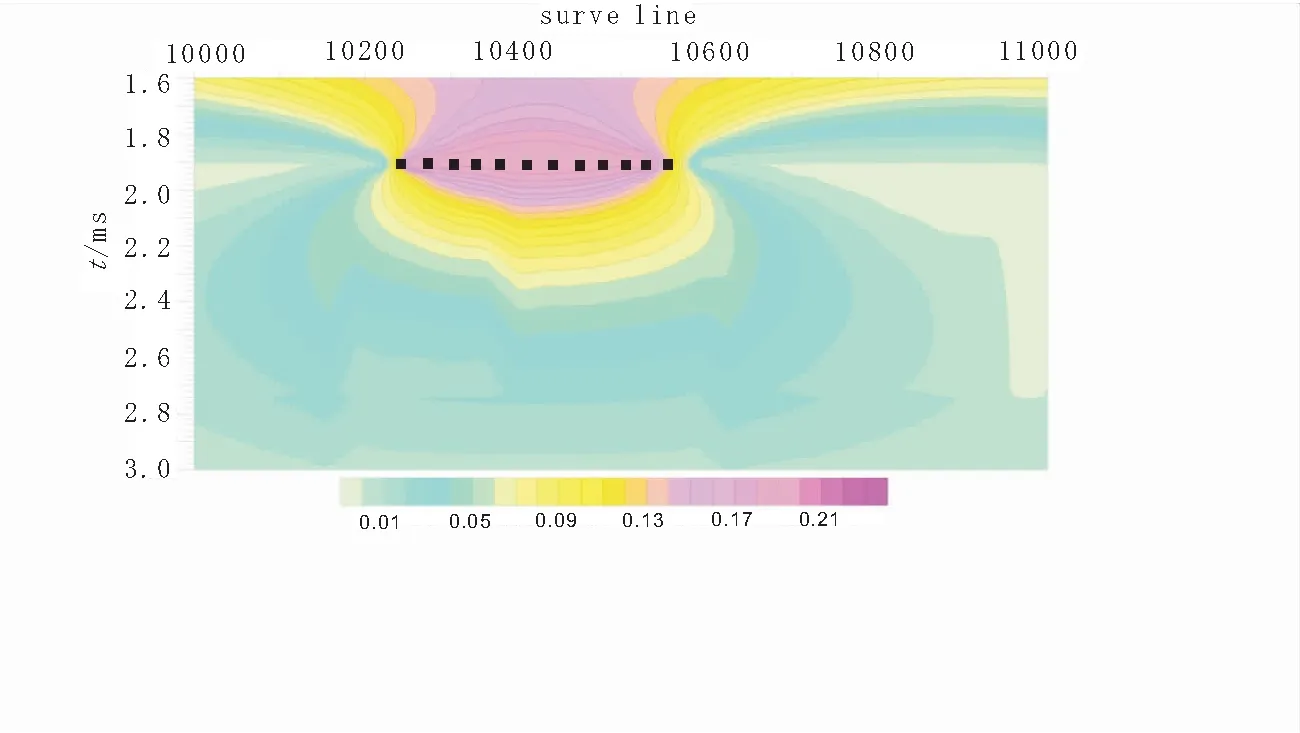
图4 测线3对应晚期道视时间常数tau/ms剖面图Fig．4 The corresponding the time constant (tau/ms) profile in the late of line 3

图5 薄板状异常体的视时间常数tau/ms的空间展布Fig．5 The spatial distribution of the apparent time constant tau/ms for the sheet abnormal body

2.2 时间常数 tau的实际应用分析

图7为某地区的实测瞬变电磁原始数据时间剖面图，仅从时间剖面图中可以看出，在测点 2 500 附近和 4 000～4 500 处有异常的响应，其中测点 2 500 附近的响应强，从早期到晚期均有响应，而测点 4 000～4 500 处，早期响应异常较明显，晚期时接近于无变化。

应用该地区瞬变电磁响应得出如图8所示的视时间常数tau在不同时间道上沿测线方向的变化规律。在图8(a)中，时间常数tau值在整个测线上都有较明显异常，在测点 2 500 附近异常最明显，与图7中所反映的异常现象相吻合，随着时间的推移，在图8中，测线两边的异常相对逐渐减弱，而突出了测点 2 500 附近的异常，由此可以得出，测线两边异常主要体现在较早期道，即相对浅部信息或与围岩差异较小的异常体；而测点 2 500 附近时间常数tau值的异常体现了较深部信息或与围岩异常差异很明显的低阻异常体，在响应上有较大的延迟。可以得出，较早期道的时间常数tau值受一次场的影响，其变化较晚期道的时间常数tau值不明显，随着时间增大，时间常数tau变化也越来越明显，最后突出反映晚期道异常体。图9为对应视时间常数tau剖面图，更能直观地反映出低阻异常体横向的分布规律，可以推断时间常数tau值异常处为一低阻异常体，与实际地质情况吻合良好。

3 结论与展望

瞬变电磁响应与时间常数密切相关，而时间常数反应着地下介质介电常数、电导率、异常体的几何形状及埋深等，因此对时间常数τ的分析有着很大的意义。作者在分析视时间常数tau的基础上得出以下三点结论：

(1)针对瞬变电磁二次场与地质异常体的响应关系，结合异常体内在的岩性和物性参数，得出了视时间常数tau成像方法，并作出了时间剖面和时间道切片，通过数值模拟和实测数据的计算，得出了较好的效果。

图6 中心时间t=1.900 ms的tau/ms值水平切片成像Fig．6 Tau/ms horizontal slice imaging at the center timet=1.900 ms

图7 某地区实验数据抽道时间剖面图Fig．7 The extractive time-windows profiles for the experimental data at a certain area

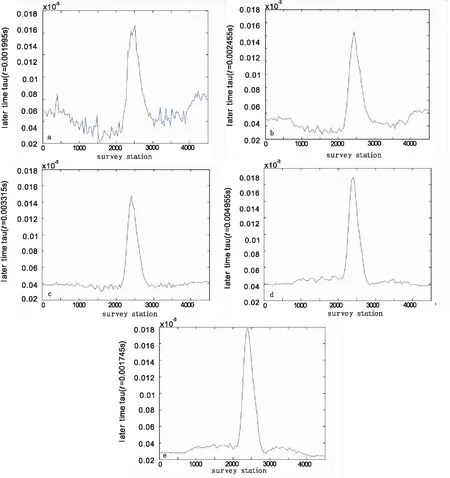
图8 某地区测线的不同时间道上tau/ms的变化规律Fig．8 Tau/ms change principles at different time on the survey line of a certain area(a)t=1.745 ms；(b)t=1.995 ms;(c)t=2.455 ms;(d)t=3.315 ms;(e)t=4.915 ms

图9 某地区视时间常数tau/us值剖面图Fig．9 A region as the apparent time constant tau/us profile

(2)通过数值模拟，得出视时间常数tau能较好地反映晚期时间道(即深部)上地质异常体横向上的分布规律，但不能很好地反应异常体的深度。

(3)对于薄板状低阻异常体，其瞬变电磁二次场在时间上有延迟效应，即地下某一深度的地质体可能影响到很长时间内的τ。那么提取的时间常数τ就不单是反应该时间窗对应的地质体，还受薄板响应的延迟影响。

接下来的工作展望，根据地质体的瞬变电磁响应规律，充分利用二次场数据，以期得出早期的视时间常数tau与瞬变电磁场的对应关系，以求取早期的视时间常数变化特征，并探索视时间常数tau与地质异常体埋深的对应关系。

参考文献：

[1] 静恩杰,李志聃.瞬变电磁法基本理论[J].中国煤田地质,1995,7(2):83-87.

[2] 静恩杰,李志聃.瞬变电磁法资料处理和解释[J]. 中国煤田地质,1995,7(4):97-101.

[3] 牛之琏.时间域电磁法原理[M].长沙:中南大学出版社,2007.

[4] JIUPING CHEN, JAMES MACNAE. Automatic estimation of EM parameters in Tau Domain[J]. Exploration Geophysics，1998,29:170-174.

[5] SOTT J. HOLLADAY,WILLIAM E. DOLL,LES P. BEARD,et al.UXO Time-Constant Estimation from Helicopter-Borne TEM Data[J].Journal of Environmental and Engineering Geophysics，2006, 11(1):43-52.

[6] 郑凯.回线源时间域航空电磁数据处理研究[D].成都:成都理工大学,2010.

[7] PELTON W H.Mineral discrimination and removal of inductive coupling with multifrequency IP[J]. Geophysics,1987:201-205.

[8] DANIEL LEMIRE,PH D. Baseline asymmetry, Tau projection, B-field estimation and automatic half-cycle rejections[M]. Signal processing and industrial R&D consultants,2011.

[9] ALLARD M. On the Origin of the HTEM Species. Advances in Airborne [J].Geophysics.2007:355-374.