“三定法”教你轻松搞定函数图象共存问题

白银市第十中学 高丽娟

1 引言

图象与性质是函数中难以剥离的两个内容，要想提高函数整个知识点的理解与运用程度，就离不开分析它的图象和性质[1].所以，本文中推出“三定法”，尝试探究与分析函数图象的共存问题，以帮助学生扫除“障碍”.

2 理论基础

函数图象共存常涉及正比例函数、一次函数、反比例函数、二次函数的图象，是同一直角坐标系中一种或多种图象的综合.所以，要想解决图象共存问题，先要弄清楚这几种函数的图象及性质，详见表1.

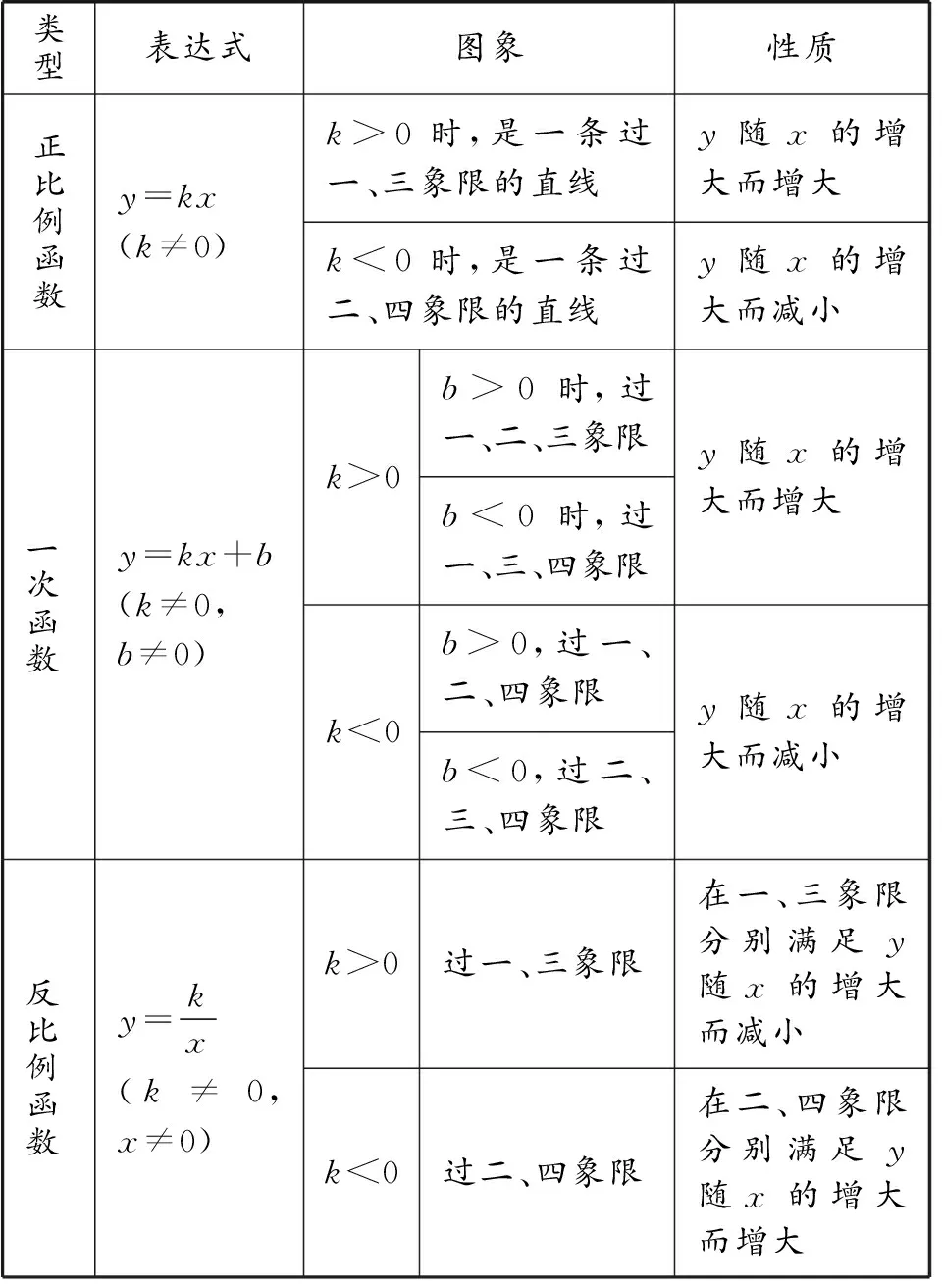
表1

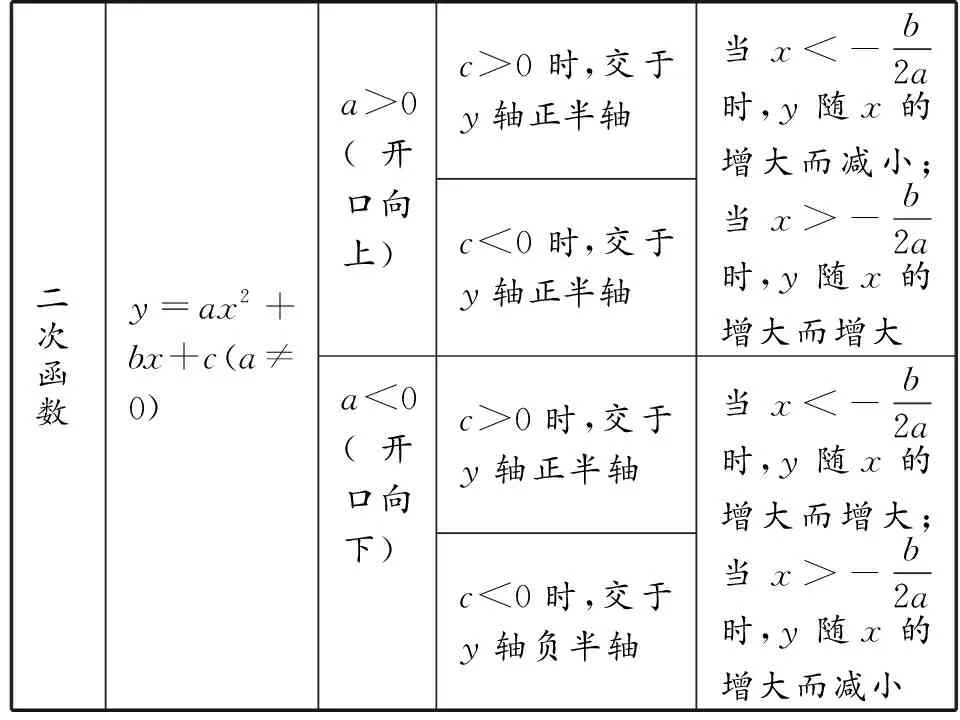
(续表)

3 “三定法”说明及例析

本文中所指的“三定法”，是解决函数图象共存问题的一种方法，主要有如下三个步骤：

第一，定图象.由于函数图象共存问题中常出现两个图象，所以以哪个图象为基础分析问题非常关键.选择哪个图象并没有定法，可据题意灵活选择.

第二，定符号.在选择基础图象后，就要根据该图象分析出相应系数的符号.如分析正比例函数中k的正负、一次函数中k和b的正负、二次函数中a和b，c的正负等.

第三，定结论.在定好基础图象对应的系数符号后，就需要将之与另一图象对比.若系数的符号在两个图象中一致，则图象可共存；反之，则图象不可共存.

本方法的三个步骤具有一定的顺序，在分析问题时，只要任何一个顺序错误，利用本种方法分析问题将无法达到预期效果.

下面，结合例题分别从正比例函数和一次函数图象、一次函数和反比例函数图象、一次函数和二次函数图象等几种共存情形出发，具体分析如何解决图象共存问题.

3.1 正比例函数和一次函数图象共存

例1如图1,函数y=kx-k2和y=-kx(k为常数，且k≠0)在同一坐标系中的图象可能是( ).

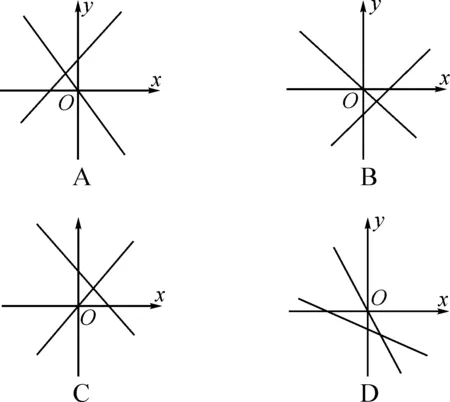
图1

解析：选项A中的正比例函数过二、四象限，所以-k<0，那么k>0.再看一次函数图象，它过一、二、三象限，所以k>0，这一点与正比例函数中的k保持一致.如果k>0，那么-k2应该小于0，所以一次函数的图象应该与y轴的负半轴相交.但是选项A中一次函数图象与y轴交于正半轴.这一点矛盾，所以选项A错误.

选项B中的正比例函数也是过二、四象限，所以-k<0，那么k>0.再看此时的一次函数图象，它过一、三、四象限，所以k>0，这一点与正比例函数中的k保持一致.如果k>0，那么-k2<0，所以一次函数的图象应该与y轴的负半轴相交.选项B中一次函数图象与y轴正好交于负半轴，所以选项B正确.

选项C中的正比例函数是过一、三象限，所以-k>0，那么k<0.在同一平面直角坐标系中的一次函数的图象过一、二、四象限，所以k<0，这一点与正比例函数中的k保持一致.如果k<0，那么-k2<0，所以一次函数的图象应该与y轴的负半轴相交.然而，选项C中的一次函数图象却与y轴正半轴相交，由此判断C错误.

选项D中的正比例函数是过二、四象限，所以-k<0，那么k>0.在同一平面直角坐标系中的一次函数的图象过二、三、四象限，所以k<0，这一点与正比例函数中的k相反，矛盾.所以选项D错误.

故本题应选：B.

评析：在分析本题中的每个选项时，“三定法”得到了完美展现.首先，确定正比例函数图象为基础图象，然后分析k的正负符号，再与另一直线对比寻找符号是否一致.从中也可以发现，用“三定法”分析图象共存问题时，需对每个选项逐个分析，直至找到符合题意的选项.

3.2 一次函数和反比例函数图象共存

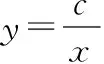
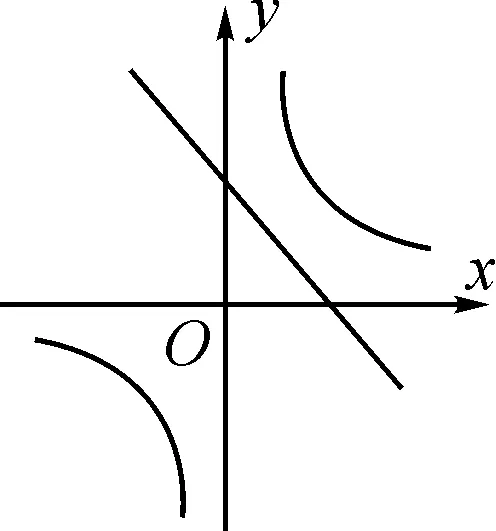
图2

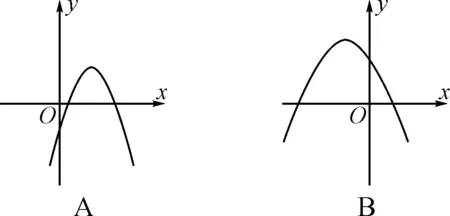
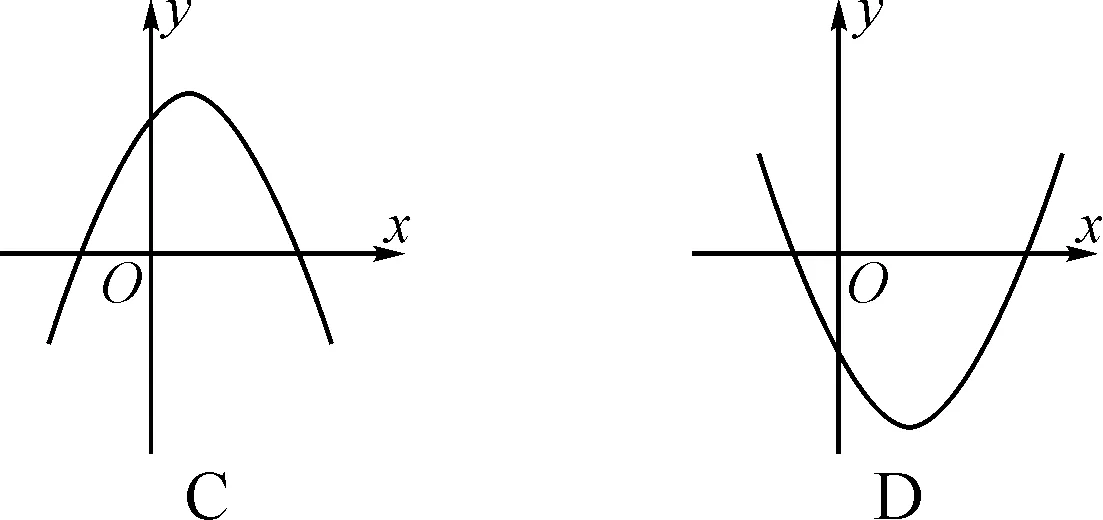
图3

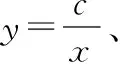
评析：这是近几年中考考查图象共存问题比较新颖的方式，与例1常规考法有较大差别，但“三定法”同样适用，只是需作灵活处理.所以，在基础题上作适当延伸和拓展，对学生掌握“三定法”有利.

4 “三定法”的注意事项

首先，函数图象共存问题中，通常会画出若干种函数的图象.学生在分析这类问题时，始终要注意分辨，不能混淆图象，更不能将系数的正负符号分析错误.

其次，函数图象共存问题有多种不同的类型，无论是哪一类图象共存问题，它们的解题方法都可利用本文提到的“三定法”.对与例2类似的图象共存问题，则需根据所给出的图分析出系数正负符号，然后再与所给选项对比，该类问题考查形式相对更加灵活，需引起注意.

最后，对于多种函数解析式中相同的字母，它们的正负符号也一定相同.如例1中的“一次函数y=kx-k2和正比例函数y=-kx(k为常数，且k≠0)”，这里的k不仅是比例系数，而且-k2构成了上述所讲的b.分析时，一定要将此分离开，切忌混淆.

5 结语

总之，“三定法”作为本文提出的一种解决函数图象共存问题的方法， 在整个使用过程中，要准确把握与函数图象及性质有关的理论基础，这是三定法”解决问题的依据，只有这样才能分析两个函数图象是否存在矛盾之处，找到正确答案[2].