浅谈初中生数学运算素养的培养

江苏省苏州市吴中区木渎实验中学 唐婷颖

1 引言

数学运算素养是义务教育阶段新课程标准提出的数学学科核心素养之一[1]，是数学运算知识技能、数学思考、问题解决和情感态度等的有机整体.扎实的运算知识、熟练的运算技能是数学运算素养的显性表现，而深度的数学思考、积极的情感态度则是数学运算素养的隐性因素，四者相互影响，彼此融合.培养学生数学运算素养是初中数学教学的重要任务，初中生的数学运算素养的培养也应该重点关注以上几个要素.

2 运算素养培养要素

2.1 积累运算理论，扎实数学运算基础

知识是素养的基石，一个人没有深厚的学科理论知识就很难形成良好的学科素养.提升学生的数学运算能力，培养学生数学运算素养，要重视运算理论知识的积累：其一是数学运算知识——算理、算法、算序、算技等，其二是数学运算理论知识间的联系与区别.

2.1.1 认知运算理论知识

算理是数学运算的意义和基本原理.准确理解运算基本原理，是运算结果正确、运算方法精准和运算过程合理的保证.

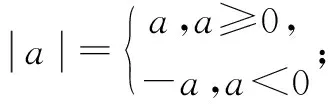
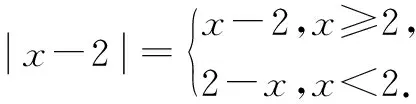
在数学运算教学中，我们还要重视算法、算序和基于运算律、运算公式生成的运算技巧等.例如，学生常有“(x+2y)2=x2+4y2”这样的“经典”错误，这种错误形成的原因是学生没有掌握完全平方公式，并且对乘法分配律理解不透彻.如果学生掌握了完全平方的算法“(a±b)2=a2±2ab+b2”，就可以直接套用公式得到(x+2y)2=x2+4xy+4y2；如果学生熟练掌握乘法分配律，那么他就清楚(x+2y)2的实质是(x+2y)(x+2y)，首先把前括号内的“x+2y”“公平分配”给后括号内的x和2y得“(x+2y)x+(x+2y)2y”，再次“分配”得“(x2+2xy)+(2xy+4y2)”，最后合并同类项得(x+2y)2=x2+4xy+4y2.

显然，数学运算不能想当然，要依据严谨的算理、算法、算序、算技等进行，否则就会导致运算方向不明、运算方法错误等.学生运算素养的培养就要从最基本运算理论知识开始.

2.1.2 辨析运算知识间联系与区别

万物总是辩证地存在着，不同数学运算理论知识间也一样存在着联系与区别，在数学运算教学中要引导学生学会辨析.

例如，学生如果明白“(a-b)2”与“(a+b)(a-b)”的运算实质都是乘法分配律，那么就不会混淆这两个运算公式了.又如，一些学生错误认为“(a+b)(a-b)=a2-b2”和“a2-b2=(a+b)(a-b)”是相同的公式.其实前者是整式乘法公式，后者是因式分解公式，是有本质区别的，只有认清了本质，才能恰当运用公式正确进行数学运算.

拥有扎实的运算理论知识是提高数学运算素养的前提.作为数学教师要引导学生理解并熟练识记各种运算定律、定理、公式等，帮助他们掌握运算理论知识的实质，并灵活应用运算理论知识进行数学运算，从而掌握正确的运算技巧，提升运算能力.

2.2 培养运算习惯，提高数学运算能力

良好的运算习惯，是学生提高运算素养的关键[2].学生运算能力差，正确率低，很多是平时运算习惯不好造成的.有些学生不重视运算，觉得麻烦，平时没必要费时间去算，考试时认真算就可以了.殊不知真到考试的时候一算就错，甚至根本没有算的能力.因此，培养学生良好的运算习惯是非常重要的环节.

2.2.1 审题与思维习惯

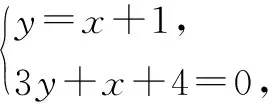
数学学习是建立在“思维”基础上的，运算素养的培养离不开良好的思维习惯.例如“因式分解：x2-4xy+4y2-1”，要顺利完成因式分解运算，学生除了要有良好的“整体思维”——把“x2-4xy+4y2=(x-2y)2”看成一个整体，还要有良好的“结构思维”——熟悉因式分解中“完全平方和”与“平方差”公式的结构形式[3].因此，我们在运算教学过程中要循序渐进地引导学生养成良好的运算思维习惯，积极思考运算方法和运算技巧，让学生明确运算的每一步该想什么，该怎么想，该怎么便捷地想，从而形成正确、简便的计算思路，不断提高自身的运算素养.

2.2.2 验算与纠错习惯

验算是验证运算是否正确的基本方法.验算的主要方法有代入检验、换序重算、逆序倒算等.平时练习和考试的过程中，只要时间允许都要求学生对一些较复杂的运算过程进行验算.

例如，验证“因式分解：x2-4xy+4y2-1=(x-2y+1)(x-2y-1)”是否正确，我们可以采用逆序倒算“(x-2y+1)(x-2y-1)=x2-4xy+4y2-1”来验证.

引导学生养成验算的习惯，是提高学生运算素养的重要环节.验算不只是验证运算结果正确与否那么简单，更重要的是长期的验算积累能形成判断运算结果正确与否的敏感性，从而增强对运算过程的掌控能力.

错题是培养学生运算素养的重要资源，运算类错题体现了学生数学运算技能的薄弱点.引导学生养成认真纠错的习惯能够让学生突破自身在运算方面的薄弱环节，形成解题过程反思的习惯.学生运算出错是不可避免的，而且很多题目本身就设置了让学生出错的陷阱，我们不可能让学生运算不出错，用好错题资源才是最重要的.

例如，“已知3x2+y2-6x=0，求x2+y2的最值”最大的陷阱在于对x范围的隐性限制——由“y2=-3x2+6x≥0”得“0≤x≤2”.教师可以通过学生的共性问题，引导学生进行解题反思，促使学生在平时运算过程中“多想一步”，减少运算失误.

在“双减”政策落实之前很长一段时间，不少教师滥用题海战术提高平均成绩，但代价是挤占学生自主探究和反思的时间，养成不懂就抄答案、运算过程简单潦草等坏习惯，扼杀了学生思维拓展和探究的欲望.因此，我们要走出题海，充分并善于利用错题资源，引导学生对自己的运算过程出错之处进行反思，填补运算薄弱点，不断提升数学运算素养.

2.2.3 书写与布局习惯

“书写”与“布局”是数学运算解答过程的门面，工整的字迹，合理的布局让人对运算过程一目了然.要求学生平时运算过程的书写要格式规范、内容有序、字迹清晰，草稿也一样.良好的书写和布局习惯有助于运算思维的发挥，有助于在运算出错时快速找到症结.但是，书写与布局习惯的培养是一个持之以恒的过程，需要有计划、有步骤地长期训练.对书写和布局做得好的学生适时给予表扬奖励，同时要给学生标准的参照范式——如教材中例题规范严谨的布局、老师工整规范的板书等.

2.3 适当运算训练，巩固数学运算素养

任何能力的培养都是需要针对性训练来巩固，为了高效地巩固提高学生数学运算素养，教师应设计科学合理、有的放矢的练习供学生训练.首先，要重视口算、速算等基本运算技能的训练，除了一些基础题的运算训练让学生熟练掌握各种运算公式、定理、技巧等，还要求学生熟记一些常用的运算结论，如常用的勾股数、特殊角的三角函数值、2与3的常用指数幂、1到20的平方、1到10的立方等等.其次，训练要有层次性，多设计一些递进式的变式题.

例如，在一元二次方程根与系数关系教学中，笔者给出了以下例题及其变式：

已知x1,x2是方程x2+2x-3=0的两个根，则x1+x2=，x1x2=.

变式2已知x1,x2是方程ax2+2x-2a-1=0(a≠0)的两个根，且x1+x2=-2，则a=，x1x2=.

俗话说“熟能生巧”，学生运算素养的巩固和提高必须通过适当强度的科学的针对性训练，做到从简到繁、从易到难，循序渐进，更要避免滥用题海战术.

3 结语

当然，没有人天生就喜欢繁杂的数学运算，培养学生运算情感也不容忽视.数学运算教学中，我们要通过激趣、奖励和示范等手段激发学生的运算情感，让学生不嫌弃数学运算，乐于数学运算.教师授课板书也要有完整规范的运算过程，给学生带来良好的示范体验，也要引导学生参考教材例题的运算范式.教学中可以通过有趣的运算情景、信息技术的加持、生活中的运算实例探究等激发学生运算兴趣，通过口头表扬、课堂运算比赛小游戏、运算竞赛与评奖等提高学生运算成就感.总之，我们需要让学生在面对数学运算时有范可学，提得起兴趣，能获得成就感，这样才有利于数学运算素养的培养.

数学运算素养不是孤立地存在的，数学运算素养是最基本的核心素养，离开了数学运算素养，其它五大核心素养就成了空中楼阁.数学运算素养培养是数学教学的基础工程，初中是学生数学运算素养培养的关键阶段，教师和学生都要重视.