本质 整体 衔接 对比——代数学习之新体验

江苏省张家港市梁丰初级中学 杨红云

1 引言

代数学习是初中数学中的重要内容，特别是对从小学刚刚进入初中阶段的学生来说，学习内容的丰富、难度的增加，让数学学习跃上了一个新的台阶.如何使学生能快速适应扑面而来的大量数学知识，需要教师注意改善学生学习中的体验[1].代数学习涉及多个方面的计算，一个细小的环节错误会导致全盘皆输，学生在学习过程中需要在多个运算法则之间灵活切换，才能使代数的学习较为顺利.但是不难发现，很多学生一开始就对各种计算感到头疼，惧怕各种数字和符号.代数学习的不顺畅严重影响了初中数学的进一步学习.笔者拟从改善代数学习体验的角度，谈一谈教学中的一些策略，供大家参考.

2 归纳总结，改善代数运算体验

数学的学习离不开计算，无论是代数还是几何，都需要和数字打交道.对思路清晰、数字敏感的学生来说，计算是“小菜一碟”，但是对大多数学生来说，计算是一件让人头疼的事，特别是在小学阶段经过大量的计算训练之后，已经产生了厌倦，面对初中的加、减、乘、除、乘方、开方各种混合运算，已经是一个头两个大，错误百出.运算规律多而杂，题型变化多样，教师需要引领学生进行归纳总结，抓住本质和规律，才能化繁为简，改善学生的运算体验.

案例1总结运算规律

在代数运算中，学生的错误主要集中在符号运算.由于初中阶段有了正负数的计算，再与乘、除相混合，学生常常丢三落四，做题时基本上是碰运气，看状态.为了改变这一现象，笔者对运算规律进行了总结.同号的两个数相加，把符号放一边，绝对值相加即可，符号不变；异号的数相加，选择绝对值大的减去绝对值小的，取绝对值较大的加数的符号；任何数与0相加，数不变.让学生记住运算步骤，先看符号再计算.

规律的总结使学生在无穷的计算题中找到了一条出路，透过现象看本质，改善了学生的学习体验，提升了学习效果，从而也增强了学习的信心.

3 全局观念，改善挑战练习体验

任何知识点都不是孤立存在的，不少知识点之间存在着紧密的联系，因此在学习数学的过程中，要注意从全局出发，从零散到整体，构建完整的知识体系.知识的学习过程是分散的知识点的学习，学生很难找到它们的逻辑关系和相互之间的联系，因此在解题时就会带来困难，特别是在一些有难度的挑战练习当中.关注整体，从全局出发，可以帮助学生进行前后知识的复习，也能对知识的内在联系有一个比较清楚的认识，从而在解决问题的过程中获得较好的体验.

案例2因式分解

因式分解的学习建立在整式计算的基础上，但是有的学生却疑问重重.

师：今天我们将学习一个新的知识，计算x2+3x+2.

生：老师，我们刚刚才学习了(x+1)(x+2)=x2+3x+2，为什么现在又要把x2+3x+2进行分解呢？

师：看来大家有很多疑问，这样翻来覆去计算有什么意思呢？我们不妨来看下面几道题.

(1)化简：(x2-2x+1)÷(x-1)；

(2)计算：(x2+y2)2-4x2y2；

(4)解方程：x2-6x+9=0.

生1：我明白了，因式分解在计算、化简还有解方程中都能起到很大的作用.

师：整式的计算和因式分解是计算的两个不同角度，但是它们同样都有非常大的作用，在代数的运算中应用是非常广泛的.

教师高屋建瓴的全局观念帮助学生打开了视野，充分感受到知识在不同情境下的具体运用，使学生形成一个比较整体的观念，为学生更加长远、踏实地学习打下了基础.数学知识的构建如采用砖块搭建房屋，教师的作用不仅仅是把知识的砖块传达给学生，还要帮助学生学会用知识的砖块搭建起高楼大厦.可见全局观念，整体把握的重要性.

4 关注知识衔接，改善求解方程体验

初中生都有一定的知识基础，在教学中，要遵循学生已经会的就不再讲解，否则就是浪费课堂时间，也使学生提不起兴趣.注意知识的前后衔接，还能使学生感受到是在进一步学习较为熟悉的知识，能增强学习的信心[2].学生已有的知识基础可能来自之前的学习，也可能来自生活的经验，这些都是教师教学的基础.关注知识衔接，注意联系生活，同样能引导学生更好地体验学习.

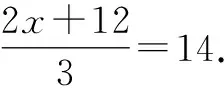
师：对于这道解方程题，书本上已经给我们推荐了一种解题方法，列表尝试法，但是老师觉得这种解法稍微有些烦琐，同学们有没有更加简便、快捷的解法呢？

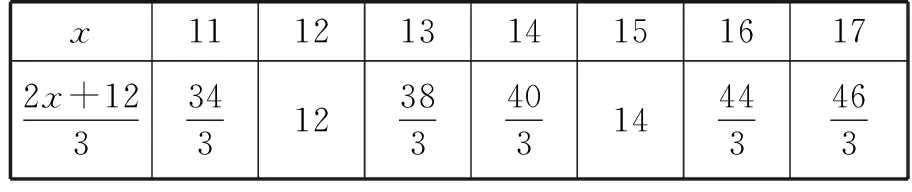
表1

生2：我们在小学里学过一元一次方程的解法，这道题可以这样转化求解：2x+12=14×3=42，由此就可以看出是我们熟悉的一元一次方程，所以x=15.

本案例中，教师并没有武断地完全按照书本上的方式尝试教学新的方程解法，而是从学生熟悉的角度出发，利用学生已经学过的知识点进行教学，避免了学生觉得以前学的知识毫无用处，重新接受一个新的知识点，增加学习负担.事实上初一阶段的很多知识点，在小学阶段已经有所了解，如坐标、图形、概率等，只不过由于学生认知水平的不同，在小学阶段可能是初步认识，或者用了学生更加容易记住的说法，与初中阶段课本的名称不一样，那么初中阶段教师要加以钻研和识别，做好知识的衔接，才能有的放矢地进行教学，改善学生的学习体验.

5 巧用辨析对比，改善解决问题体验

巧用类比思想提升学生数学核心素养.在学习数学课程的过程中，善用对比分析，可以巧妙解决很多数学问题，能以一推十，巧妙化解难题.学生往往会了一道题，碰到下一道还是一筹莫展，教学中，教师就要通过类比转化的思想，帮助学生解决一类题，而不是只能化解一道题，否则很难提升数学的学习能力.

场景1：为了保证农民生活，改善农民看病难的问题，某市积极推行医疗保险制度，将农民医疗保险的报销比例进行修订，如表2：

表2

场景2：为了扩大销量，某超市推出了如下促销方案：

(1)一次性购物不超过100元，没有优惠；

(2)一次性购物超过100元，低于400元，一律享受九折优惠；

(3)一次性购物不低于400元，一律享受七折优惠.

场景3：个人出版物缴纳个税，国家制定了方案，如下：

(1)稿费低于800元的，无须纳税；

(2)稿费在800元至5 000元之间的，需缴纳超过800元的那一部分12%的税款.

(3)稿费高于5 000元的，需缴纳全部稿费10%的税款.

师：首先，我们一起分析这三个场景，哪些需要分段计算，哪些不需要？

生3：场景2不需要分段，因为场景2最后是“一律”享受七折优惠，所以不存在分段计算.

生4：我觉得场景3最后一种情况也不需要分段，因为是“全部稿费的10%”，和“一律”是一样的意思.

师：很好，因此只有场景1和场景3的第(2)种情况需要分段计算，场景2和场景3的第(3)种情况不需要分段计算.所以我们在做这类题型的重难点就是找准题目的关键词进行判断.

对于同一类型的题目，进行对比讲解，学生能一下子明确其中的区别，认知更加直观，避免了学生碰到一题进一个坑的情况，提高了学习效率，给学生带来了较好的学习感受.

6 结束语

综上所述，学习的成果来自学生较好的学习感受，良好的学习感受能使学生感觉“数学简单、熟悉、有趣”，而不会使学生感到“数学复杂、陌生、枯燥”，激发了学生更多积极向上的能量，为学生的不断进步奠定了基础.