问题连续体 活化初中教学——谈提高初中数学教学的策略

甘肃省静宁县阿阳实验学校 杨婷娟

1 引言

初中阶段是学生学习的关键时期，也是小学数学与高中数学教育教学衔接的关键阶段.在新课改深入发展过程中，初中数学教师应积极更新教学模式，有机整合教育教学过程，以问题连续体进行各个教学环节之间的连接，从而使学生能够更快地掌握数学知识，促进学生创新思维能力及独立思考能力的提升.

2 “问题连续体”在初中数学教学活动中的应用

2.1 在概念课程内的应用

在初中数学教学活动过程中，学生既要了解和掌握概念的一般特征，又要围绕概念的确定性、发展性及层次性展开学习和理解.“问题连续体”模式的应用，可使学生从多个层次理解概念，帮助学生掌握各个概念之间的相互联系，可促进学生更为全面、深刻地掌握数学概念.教师应精心设计教学问题，并逐步引导学生.必要情况下，可充分发挥例题的作用，以帮助学生更好地巩固知识，促进学生更好地理解知识.

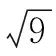
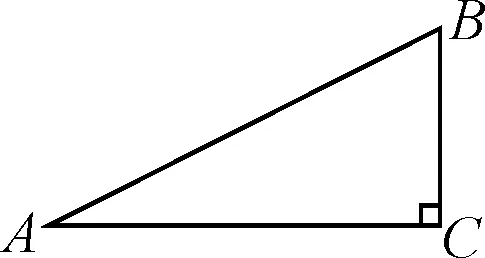
图1

2.2 在命题课程内的应用

在学习数学定理的过程中，“问题连续体”模式有助于学生系统知识体系的形成，对学生逻辑思维能力的培养与发展可起到有效促进作用，也可帮助学生在数学学习过程中更好地掌握数学思想、数学方法.将“问题连续体”模式应用到命题课程教学活动中，教师需注意引导学生有效掌握命题之间的推导过程，特别是在开展新命题学习过程中，教师需为学生提供帮助及引导，使其能够有效了解新命题与已学命题之间的联系.在实际开展推导过程中，也可深化学生对命题的理解.

例如，在学习勾股定理这一课程教学内容过程中，教师既要使学生熟练掌握勾股定理的基本内容，也要指导学生推导勾股定理.教师可利用提出问题的方式，如：当前有4个全等的直角三角形，可否将其拼成一个正方形，且正方形的边长为直角三角形的斜边？在提出问题的基础上，鼓励学生利用拼好的图形进行勾股定理证明.教师应给予学生积极的鼓励，使其更主动地参与到问题探究学习活动中.教师需预先准备直角三角形，要求学生动手实际操作，并在勾股定理证明过程中应用面积相等.学生在掌握勾股定理的证明过程后，可从基础知识层面出发展开数学定理推导，进一步深化对定理、公式的记忆及理解，大大节约学习和记忆时间，同时在理解知识的基础上开展知识记忆，对定理运用的灵活性及科学性具有重要意义.

2.3 在习题课程内的应用

习题课程教学活动需在系列问题的引导下完成，教师应结合学生认知的实际水平进行问题设置.如此，可帮助学生更好地回忆有关数学概念及命题，也能够帮助学生掌握问题转化的方法，并构建有关数学知识的联系，从而更好地解决实际数学问题.在问题设计过程中，要注重问题设计的认知梯度，也要注重各个问题之间逻辑规律的体现，从而构建结构性问题网络.在实际问题解决过程中，帮助学生更好地进行知识网络梳理，也有助于学生认知水平及能力的进一步提升.

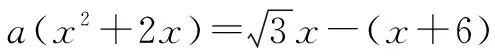
3 在初中数学教学活动中应用“问题连续体”的思考

3.1 结合学生实际学情优化调整问题设计

数学本质的体现离不开数学教学活动.在实际开展数学教学活动过程中，教师应充分考虑学生的实际状况，保证数学问题设计的合理性及科学性，在此基础上，针对学生的最近发展区展开综合性考量.在实际开展问题设计过程中，需注重把握教学重点内容，切实掌握重点和难点知识，从而最大化发挥问题教学的应用价值，不断提高数学教学的效率及质量.

3.2 结合学生思维水平进行问题导学

随着新课程改革进程的不断推进，教师应在启发性教学原则的基础上，注重激发学生自主性学习思维，同时为学生提供恰当、合理的引导，鼓励学生在参与合作学习过程中，营造互帮互助的良好学习氛围，使课堂学习任务得以高效完成.在实际开展教学活动过程中，教师应高度重视学生的反馈信息，针对学生的错误回答，教师不可急于否定，而应积极进行错误资源的有效利用，鼓励学生积极进行有效的探索学习活动，从而使教学活动的组织和开展更具针对性及科学性.

3.3 结合学生质疑进行创新思维的培养

学生创新思维的培养十分关键，鼓励学生敢于质疑更为重要.学生提出自主质疑是创新思维形成的起点，在“问题连续体”教学模式下，教师需针对问题展开精心设计，也应为学生提供质疑空间.从实际初中数学教学活动看，教师应预留学生参与课堂学习的机会，并引领学生举一反三，指导学生不断自主思考，将课堂提问的教育教学价值充分发挥出来，从而帮助学生激发数学潜能，更好地培养创造性思维及想象力.

4 结束语

综上所述，“问题连续体”模式下，更为注重数学问题的解决.应用该模式，可进一步强化初中数学教学课堂的活力，学生能够在独立思考及动手学习过程中，更深入地理解知识点，更灵活地应用知识点，这对提升学生数学问题解决能力、课堂学习效率都具有积极意义.