初中数学探究式教学的实践——以“二次函数与一元二次方程”为例

江苏省南通市如皋市白蒲初级中学 管小梅

1 引言

素质教育的不断推进要求教师不仅要注重教学方法的创新，还要提升教学方法与教学内容的契合度，从而更加深入地对数学知识进行探索.那么如何促进学生知识内化，如何改变传统教学中学生的固有思维就成为探究式教学活动应重点思考与解决的问题.

2 教学分析

2.1 教材解析

二次函数与一元二次方程是初中阶段的教学重点与难点.本章节主要引导学生通过二次函数图象解决问题，找到一元二次方程的根.相较于其他计算方法来说，该方法抽象程度较高，需要学生具备一定的知识经验与积累，并能够灵活运用数形结合的数学思想[1].

2.2 学情分析

九年级的学生已经具备了一定的探究经验，了解不同方程的解法及不同函数图象特征.该阶段学生普遍具有一定的思维能力与推理能力，但仍有较大的进步空间.基于此，本文尝试借助图象开展探究活动，促进数形结合思想的渗透与应用.

2.3 教学目标

(1)找到二次函数与x轴交点个数、一元二次方程解的个数之间的关系；

(2)能够结合二次函数图象对一元二次方程的根进行判断；

(3)学会使用对立统一的观点渗透数形结合思想.

2.4 教学重点

(1)基于一元二次方程根的求解对二次函数的图象进行二次研究，并通过二次函数图象的应用加强学生关于一元一次方程求解的记忆；

(2)数形结合，找到二次函数图象与一元二次方程根之间的关系.

3 初中数学探究式教学实践

3.1 问题引入，渗透知识

新课程标准改革背景下，教学设计需要凸显教育价值，且符合该阶段学生思维发展逻辑.通过问题引入，回顾一次函数与一元一次方程，从而顺利实现知识过渡，引导学生对二次函数及一元二次方程产生疑问，从而为本课程教学提供新的入手点，在问题的驱动下直击教学重点.

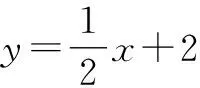
(2)一次函数y=kx+b(k≠0)中的x与一元一次方程kx+b=0(k≠0)的x有什么区别，上述两式所考虑的问题重点分别是什么？

(3)总结一次函数与一元一次方程之间的关系.

分析：一次函数中的x代表未知数，整个函数主要是对x与y的变化规律进行探究.一元一次方程更多的是寻找基于相等关系的已知量与未知量的关系，即侧重于寻找方程的解.通过对数学概念的研究找到问题探究的价值，符合初中阶段学生的认知特点，同时与课程教学目标紧密相联，对学生思维发展及学习方法掌握具有积极作用.除此以外，从较低的起点逐渐提升高度，与新课程标准改革提出的“基础与综合”的教学要求相适应.

3.2 经验链接，自主建构

结合一次函数与一元一次方程的学习经验，对二次函数与一元二次方程进行类比，并通过数形结合的方式找到二次函数与x轴的交点、一元二次方程的解.从学生的学习经验出发，降低学习难度.

问题2分别画出二次函数y=x2-2x-3,y=x2-2x+1，y=x2-2x+2的图象，并思考下列问题.

(1)观察图象，思考方程x2-2x-3=0，x2-2x+1=0，x2-2x+2=0的根的个数及方程的解；

(2)总结二次函数图象与一元二次方程的根之间的关系.

分析：通过图象引导学生对一元二次方程根的情况进行判断，潜移默化中对一元二次方程的求解方法进行思考，同时通过自主探究与思考强化学生应用二次函数图象的意识，为数形结合思想的形成奠定基础.具体教学思路如图1所示：

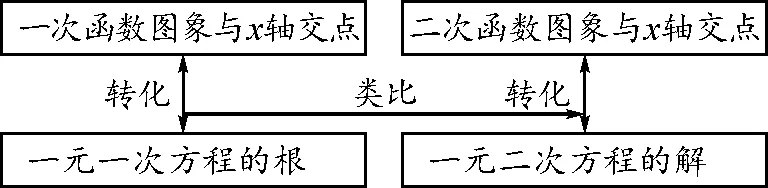
图1

3.3 数形结合，优化思维

数形结合思想的重点是看形思数，见数想形.在掌握一定数学知识的基础上启发学生自己完成抛物线的绘制，并通过图形观察解决问题，明白y=ax2+bx+c中的系数a才是决定二次函数开口方向的关键，尝试通过二次函数基本特征的总结与概括找到新的问题探讨点，引导学生更加深刻地体会函数与方程之间的必然联系.

问题3已知图2、图3、图4为二次函数y=ax2+bx+c的图象，对称轴均为x=3.

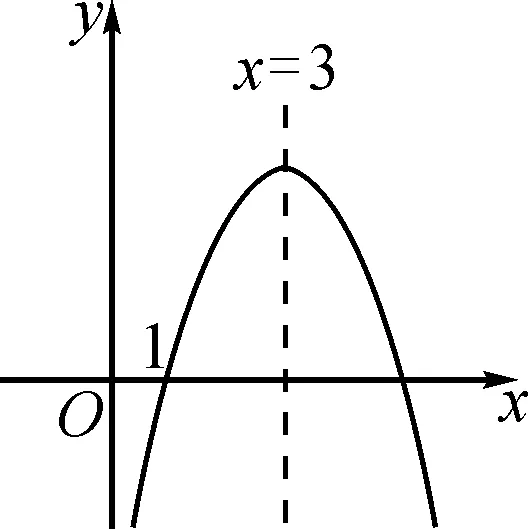
图2

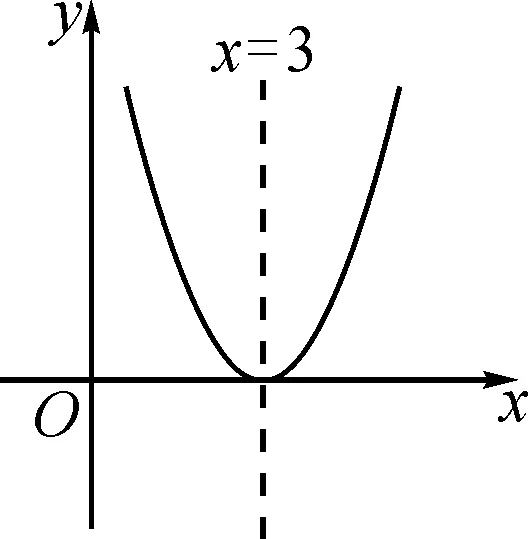
图3

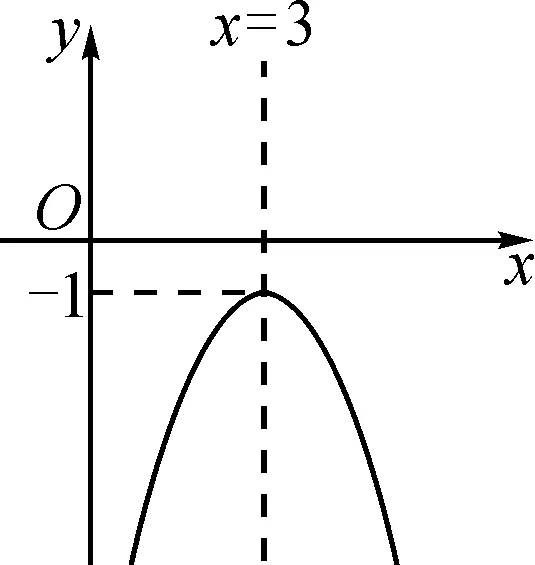
图4

(1)观察上述图象，令y=0，找到抛物线上纵坐标为0的点，并尝试求方程ax2+bx+c=0的根.

(2)若图4是关于x的一元二次方程，且方程ax2+bx+c-m=0的解为两个不相等的实数，求m的取值范围.

(3)类比上述结论，提出新的问题.

分析：该题目的解答需要学生尽可能多地找到图中的有效信息，并对不同的图象进行对比，通过不同问题的解决找到函数与方程之间的内在联系，让学生感受到二次函数与一元二次方程问题的解题方法，并尝试从方程、不等式等角度进行思考.

3.4 螺旋递进，解答疑惑

螺旋递进式地解决问题并进行变式提问，能够引发学生关于二次函数与一元二次方程知识更加深刻的思考，同时变式提问过程也在潜移默化中引导学生将数转化为形[2].

问题4已知二次函数y=x2-4x+k+2的图象与x轴有公共点，试求k的取值范围.

结合上述问题再进行以下变式与延伸：

变式1若二次函数y=x2-4x+k+2的图象与x轴有两个交点，k的值如何？

变式2已知二次函数y=x2-4x+k+2图象与x轴两交点的距离为2，求k的值

变式3若二次函数y=x2-4x+k+2图象顶点到x的距离为2，k的值如何？

引申1假设y=x2-4x+k+2是函数值恒大于零的二次函数，k的取值范围是怎样的？

引申2k取何值，二次函数y=x2-4x+k+2的图象与直线y=x-1只存在一个交点？

分析：上述问题的探讨重点是二次函数y=x2-4x+k+2与x轴的交点，通过该问题的探讨引申出二次函数与直线交点的相关问题，是对二次函数与一元二次方程问题解答步骤的再次强调.引申问题的提出逐渐过渡到高阶思维，重点考查学生解决问题的方法.

3.5 延伸探究，优化结构

延伸探究是一个不断积累、不断创造的过程.已知题目内容与一元二次方程的解有关，通过概念类比，寻找问题解决的入手点.

问题5图5为二次函数y=x2+bx+c与y=x的图象.以下结论哪些是正确的？

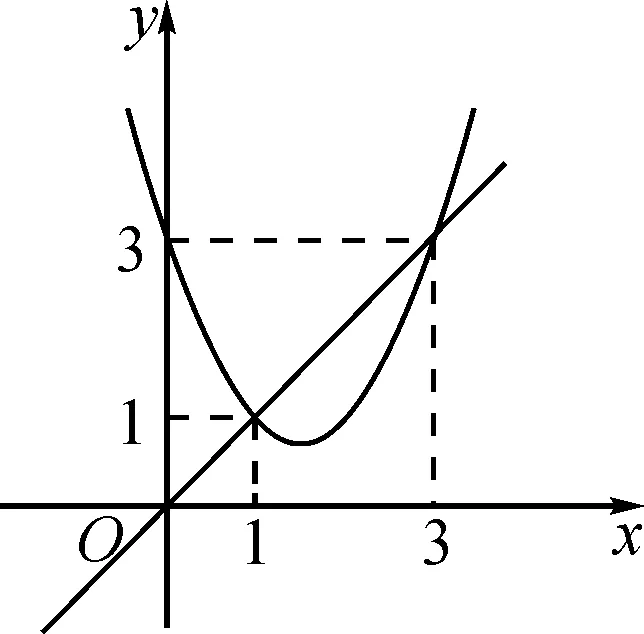
图5

(1)b2-4c>0；

(2)b+c+1=0；

(3)3b+c+6=0

(4)当1

分析：该问题设计鼓励学生以个人或小组为单位进行探究，既是对二次函数知识体系的整理，也能够强化学生对该部分知识的吸收与方法汇总.

3.6 技术辅助，高效探究

由于二次函数与一元二次方程课程教学内容较多，且抽象程度较高，采用传统的教学方式难以实现教学突破，构建探究式教学模式难度较大.基于此，教师可以借助《几何画板》等技术辅助教学，刺激学生产生主动探究的欲望，优化教学内容与过程.例如，课程导入阶段教师可通过多媒体设备为学生播放小球飞行的视频，并通过《几何画板》进行还原，帮助学生深度理解.

4 结束语

新课程标准改革背景下，初中数学教学过程应与学生认知特点相吻合.该阶段探究活动的开展并不仅仅是教学方法上的创新，更多的是通过知识的构建促进学生思考、交流，并通过上述问题寻找数学知识的本质，形成新的数学思想，使复杂度高的问题得到简单处理.