“数学建模”核心素养试题分析与命题探索

倪 黎，茹 凯，颜宝平

“数学建模”核心素养试题分析与命题探索

倪 黎，茹 凯，颜宝平

（铜仁学院 大数据学院，贵州 铜仁 554300）

高考数学核心素养测评研究中“数学建模”素养考查相对薄弱．用案例分析法对2016—2021年高考数学试卷中考查“数学建模”核心素养的试题从分值特征、题型特征、背景特征、模型特征、素养特征、阶段特征6个角度进行系统分析，从纵向（难度层次性）和横向（素养综合性）两个方向探索命题的多样性．研究表明：高考命题时应注意“题型灵活性与阶段差异性结合，改变难度层次性；背景丰富性与模型广泛性结合，实现素养综合性”．

数学建模；核心素养；试题分析；命题；案例分析法

1 问题提出

普通高中培养目标指明，要进一步提升学生综合素质，着力发展核心素养[1]，但不同角度的高考数学核心素养测评研究均反映出一个共性：各核心素养以及具体表现的考查分布不均衡，其中对“数学建模”核心素养的考查较少，甚至没有考[2-6]．由此产生了一个亟待解决的问题：“加强命题技术研究，全面考察学生的学科素养．”[3]这一现象在最新的2020年高考测评中依然存在，“加强命题技术研究，全面落实学生学科素养的考查”[6]再次被提出来．

数学建模在中学阶段的重要性日益突出，但专门针对“数学建模”核心素养试题的研究较少，更多的是综合研究六大核心素养时涉及数学建模[2-7]，或是其它视角下的分析与数学建模有关[8-11]．特别地，文[12]从分布特征、背景特征、模型特征3个方面，研究了2013—2017年全国卷中体现数学建模思想的试题；文[13]剖析了2019年高考数学中考查数学建模的7类模型．

受以上论文启发，并注意到已有研究很少以数学建模为主线进行跨年度跨试卷的多角度比较，而高考数学真题凝结了命题人的智慧可反复挖掘，同时又存在“数学建模”核心素养考查薄弱现象，很有必要继续探索其命题多样性．

2 研究思路

2.1 样本选取

每年更新的高考试题能灵敏地反映国家意志带来的变化，这使得高考处于教育改革的前线．2014年9月，国务院颁布了《关于深化考试招生制度改革的实施意见》，这是恢复高考以来最系统、最全面、最深刻的高考改革，为此教育部考试中心2016年探索构建高考评价体系，从顶层设计回答“为什么考、考什么、怎么考”的考试本源性问题[14]．此外，中国学生发展核心素养研究成果于2016年9月正式发布，随后“数学建模”出现在教育部2018年1月制定的《普通高中数学课程标准（2017年版）》中，成为数学学科的六大核心素养之一．

考虑到上述时代背景深刻影响着近几年高考，每年的高考真题也是除教材外的重要学习资源，故选取2016—2021年31个省（自治区、直辖市）高考数学84套试卷，研究其中考查“数学建模”核心素养的202道试题，涉及81套试卷．由于数学建模是对实现问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的素养[1]，因此，试题是否来源于现实问题是入选样本的关键依据．

2.2 研究方法

针对试题样本，采用定量分析与定性分析法，结合案例分析法，从分值特征、题型特征、背景特征、模型特征、素养特征、阶段特征6个角度进行试题分析，观察现有高考真题特点，了解命题现状，在真题中学习并探索命题多样性．

为表述简便，除特别注明外，后文研究的试题均指近6年高考数学真题．

3 试题分析

3.1 分值特征

“数学建模”核心素养试题在试卷中所占比重可以反映高考对数学建模的重视情况（见表1），2016—2017年平均比重为12.8%，2018—2021年平均比重为12.9%，且2016年未考查数学建模的试卷，此后加强了考查．说明高考试题一直重视对数学建模思想的考查，2017版新课标颁布后重视度稳步提高．据此推测，在“五育并举”和“加强应用型、创新型人才培养”的呼吁下，“数学建模”核心素养试题的比重还会加大．

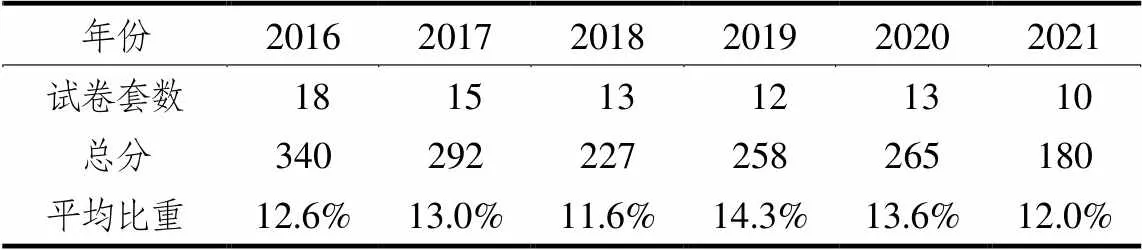
表1 “数学建模”核心素养试题分值特征

近6年，38套全国卷全部考查了“数学建模”核心素养，分值平均比重15.3%，46套地方卷中有43套考查了“数学建模”核心素养，分值平均比重10.7%，说明全国卷比地方卷重视程度更高．其中2020年新高考Ⅰ、Ⅱ卷考查题量最多且分值最高，比重均为24.7%，是考查“数学建模”核心素养的典型试卷．

3.2 题型特征

高考数学试卷的题型可以分为小题和大题两大类，小题包含填空题、单项选择题、多项选择题等，大题是指解答题．分析每套试卷的题型特征，可以从宏观上了解现有命题特点．

经统计（见表2），发现“数学建模”核心素养试题涵盖了高考数学的所有题型，试卷中大题搭配小题模式有63套（77.8%），是主流命题形式，“1大5小”首次出现在2020年新高考全国Ⅰ、Ⅱ卷中．2020年新高考全国Ⅱ卷第9题首次以多项选择题考查“数学建模”核心素养，2020年北京卷填空题第15题可以看作是不定项选择题的雏形．另外，2021年1月的八省联考数学试卷中已经出现了“2大2小”，说明“多大多小”题型特征可以实践．

表2 “数学建模”核心素养试题题型特征

3.3 背景特征

数学试题与不同背景结合形成不同的实际问题，近6年高考数学考查“数学建模”核心素养的202道试题，涉及生活生产、音乐建筑、天文地理、历史文化、生态环境、生物实验、交通运输、医疗卫生等背景，显示了数学广泛的应用性．表3从学生校园生活角度统计，将问题背景属于校园生活的视为“内”，校园外的视为“外”；又从时间层面统计，将当代视为“今”，当代之前视为“古”．

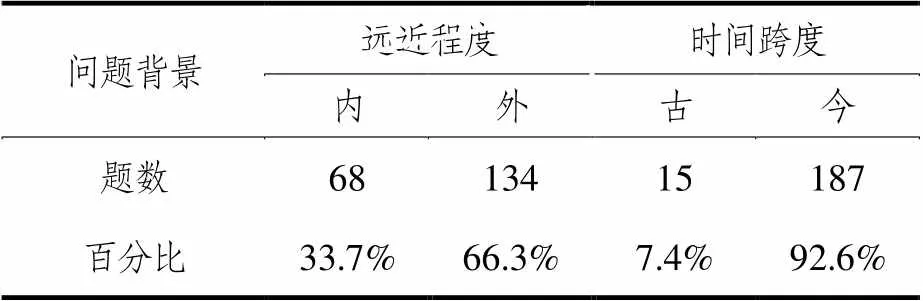
表3 “数学建模”核心素养试题背景特征

校园是学生生活的主要场所，受到了特别关注（33.7%），能触动学生运用数学知识解决身边问题的兴趣和信心．校外世界更加丰富多彩（66.3%），无论是居民用水问题，还是新药疗效比较，部分问题来源于科学研究，具有学术价值．从时间上看，试题背景既兼顾了古籍、古迹等古文化中的数学元素与数学视角（7.4%），更突出了时代特点（92.6%）．如2016年的节约用水，2017年的共享单车，2018年的新农村建设，2019年的嫦娥四号探月工程，2020年的新冠肺炎疫情，2021年的北京冬奥会志愿者培训，不胜枚举．彰显了高考评价体系的“立德树人、服务选才、引导教学”核心立场，形成了问题背景与数学知识合力育人效果，发挥了高考数学的育人价值．

考查“数学建模”核心素养的试题，由近及远、从古至今勾勒出一幅精彩世界的图景，给学生提供了“未出校园、心怀天下”的窗口，也为师生从数学角度发现问题和提出问题打开了思路，具有教学价值．

3.4 模型特征

实际问题与不同数学知识结合形成不同的数学模型，按照建立模型的主要数学方法（或所属数学分支）[15]进行分类统计，得到表4．

表4 “数学建模”核心素养试题模型特征

概率统计模型是体现“数学建模”核心素养的主力军（62.9%），考查从未间断，覆盖全国卷和地方卷，涉及所有题型且解答题较多（60道）．全国卷与地方卷近6年都在考几何模型（11.9%），其中江苏卷（2016—2020年）贡献最多，独具特色，代表性强．剩下7类模型的考查相对较少（25.2%），其中解答题只有5道，考查不稳定，不够重视．

考查“数学建模”核心素养的试题，为数学知识的应用提供了示范，学生可以由此见识同一模型在不同实际问题中的应用，以及不同模型在同一背景中的应用，再次凸显数学强大的应用性．这些眼界与体悟犹如一粒粒种子，等待着在未来解决各行各业现实问题中生根发芽、开花结果，有利于激发学生解决广阔世界中复杂问题的内生动力和立志打牢数学基础的坚定决心．

3.5 素养特征

数学学科的六大核心素养，是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现，它们之间既相对独立、又相互交融，是一个有机的整体[1]．在近6年高考数学考查“数学建模”核心素养的试题中，普遍存在同时考查其它核心素养的现象，统计结果可通过雷达图直观展示（见图1），又从另一个角度，统计了每道试题中包含“数学建模”在内的核心素养考查个数（见图2）．

图1 “数学建模”核心素养试题素养分布

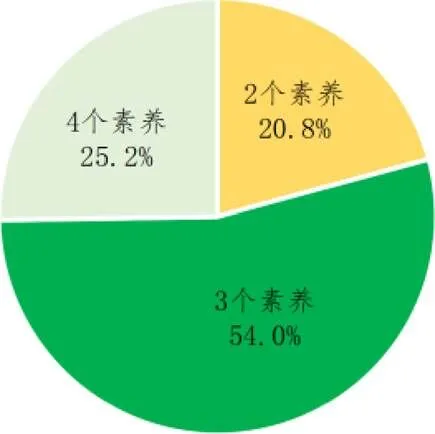
图2 “数学建模”核心素养试题素养考查

由图1可知，近6年高考“数学建模”核心素养试题遍及六大核心素养，体现了高考评价体系的“核心价值、学科素养”考查目标．图2表明，所有试题都考查了包含“数学建模”在内的多个核心素养，说明“数学建模”对其它核心素养的依赖程度强，与已有研究结果一致[16]．

考查“数学建模”核心素养的试题，对六大核心素养的考查具有较强的综合性，在考查“数学建模”核心素养的同时，还能兼顾其它核心素养，反之则不然．值得加大考查力度，这正是缓解试卷中各核心素养考查不均衡状况的有效途径．

3.6 阶段特征

不少研究已对数学建模阶段进行了很成熟的划分[17]，受此启发，注意到考查“数学建模”核心素养的试题有别于一般意义下的数学建模，为此，针对试题特点，用上游问题、中游问题和下游问题来进行区分比较，见表5．

表5 “数学建模”核心素养试题建模阶段划分

这3个建模阶段可简称为“上游”“中游”“下游”，与数学建模活动的基本过程[1]之间的关系见图3．

图3 数学建模活动的基本过程与建模阶段

统计近6年高考“数学建模”核心素养试题的建模阶段（见图4）发现：不同阶段的试题比重不平衡，以中下游为主（97.0%），中游居多（80.7%），上游最少（3.0%）．中下游（196道）覆盖了所有题型，分值高、背景广；上游（6道）只涉及单项选择题和填空题，除去2道文理科试卷同题，只有4道代表性试题．

图4 “数学建模”核心素养试题建模阶段

下游的特点是模型已经建立，主要考查模型的应用，易于学生入手．对于尚未学习的复杂模型，也可以让学生应用模型解释或解决实际问题．如某地区新冠肺炎累计确诊病例数的Logistic模型（2020年全国Ⅲ卷文、理科第4题），该题还显现了数学在疫情防控中活跃的身影；又如新、旧设备生产产品的某项指标比较问题（2021年全国乙卷文、理科第17题）．

中游的主要任务是建立、求解、检验模型，重点考查学生运用所学知识解决实际问题，是数学建模的核心环节，需要不断强化训练，因而考查比重最多．传统应用题主要处于中游，中游可以自然延伸到下游、追溯到上游．

上游源于“在实际情境中从数学角度发现问题、提出问题”[1]，不过呈现在试题中的都是命题人发现并提出的问题，重点考查分析问题的建模准备阶段，靠近中游，目前的4道考题难度不大．但在问题提出之前的混沌状态，或许只是大千世界的平凡现象，如啤酒与尿布，培养学生用数学的眼光发现和提出问题，已经是在培养学生跨学科创新的高阶思维了．由于上游不涉及模型求解，更复杂问题的初始分析阶段也能在此考查．因此，上游可考查的范围最广，也最难．

考查“数学建模”核心素养的试题，展现了不同的建模阶段．无论是往上游方向回溯、还是往下游方向推进，都将面临未知的困难与挑战，需要注重知识储备、经验积累，更需要勇于探索的精神、攻坚克难的毅力，还需要一定的洞察力、想象力[15]，能很好地磨砺学生意志、培养创新精神．

4 命题探索

2020年1月，教育部考试中心正式发布了《中国高考评价体系》，告别了高考考试大纲，该评价体系由“一核”“四层”“四翼”组成，“四翼”回答了“怎么考”的问题，给出了高考考查要求：基础性、综合性、应用性、创新性．另外，《普通高中数学课程标准》中数学学业质量水平二是高考的要求，也是数学高考的命题依据[1]．

“数学建模”本身就是能够承载基础性、综合性、应用性、创新性的有效载体，下面针对高考数学试卷中“数学建模”核心素养考查薄弱现象，从纵向（难度层次性）和横向（素养综合性）两个方向，探索命题多样性．

4.1 题型灵活性与阶段差异性相结合以改变难度层次性

探索纵向命题时，先不考虑横向的变化．

4.1.1 题型灵活性

下面以一道高考真题为母题，进行封闭式和开放式子题改编．

案例1（2020年全国Ⅰ卷文、理科第5题）某校一个课外学习小组为研究某作物种子的发芽率和温度（单位：℃）的关系，在20个不同的温度条件下进行种子的发芽实验，由实验数据(x,y) (=1, 2,…, 20)得到下面的散点图：

由此散点图，在10℃～40℃之间，下面4个回归方程类型中最适宜作为发芽率和温度的回归方程类型是（ ）

A．=+B．=+2

C．=+eD．=+ln

这是一道考查学生观察散点图、建立非线性回归模型的问题，以选择题形式巧妙地“减少运算量，增加思维量”[18]．该题事先设计好了标准答案，是一道常见的封闭式问题．在学生明白这类模型求解原理的前提下，相比于套公式进行复杂的计算，能从中察觉出散点图与对数函数的关联，发现隐藏在数据背后的规律并将现实问题转化为数学问题，更考验学生的思维过程与创新意识．通过题型的灵活变化能实现命题多样性，下面给出变式子题．

变式1 改为单项选择题．（封闭式）

为研究某作物种子的发芽率，下列哪项因素是最重要的？给出种子的价格、种子的重量、种子的直径等次要因素，以此来考查数学建模中假设的合理性．

变式2 改为多项选择题．（封闭式）

考虑到该题直接改为多项选择效果不好，尝试换个角度．比如，某校一个课外学习小组为研究某作物种子的发芽率，计划在不同的温度条件下做种子的发芽实验，需搜集哪些数据进行有效分析？可以给出实验次数、种子样本量、实验日期、实验人数等干扰选项，考查学生能否在较多数据中抓住主要矛盾，选取合适的指标变量．此时也可以直接改为不定项选择题．

变式3 改为填空题．（封闭式）

将该题直接改为填空题，缺少了选项部分的提示，难度增大了．

为“逐渐减少选择题、填空题数量”[1]，还可以改编为解答题．

变式4 改为解答题．（封闭式）

题干补充具体数据，要求学生建立并求解发芽率和温度的回归方程，也可以进一步要求学生求出发芽率最高的温度是多少．这种改编能更全面地考查建立与求解模型，但计算量较大．

除了封闭式问题的改编，也可以“以开放式问题打破定势思维”[9]．在相同观点下，举例开放；在共同结论下，条件开放；对同一问题，研究方法开放；对同一问题，思维层次开放[10]．从而“改变相对固化的试题形式，增强试题开放性，减少死记硬背和‘机械刷题’现象”[19]．

变式5 改为解答题．（开放式）

题干直接给出发芽率和温度的多个回归方程，至少包含对数回归方程，用统计表（或统计图）给出数据，甚至给出常用软件（如Excel）的回归分析结果，由学生来比较模型的优劣，并给出理由，然后运用模型．这种改编借鉴了2018年全国Ⅱ卷文、理科第18题的命题手法，能让学生“多想一点，少算一点”．

以上改编仍属于结构良好问题，条件不多不少．当一个好的现实问题被发现并提出来以后，学生真正去建模解决问题时，往往面临数据缺失、难以继续或数据过多无从下手的困境，这是建模中较难的一个环节，却又是平常教学中很少涉及的．结构良好问题在日常学习与训练中不可或缺，但结构不良问题更接近真实世界，能考查学生思维的系统性、灵活性、深刻性、创造性[20]．下面尝试减少条件或增加已知，改编为结构不良问题．

变式6 改为填空题．（开放式）

某作物种子的发芽实验数据整理如下，从中任选两个条件补充到下面问题中，若回归方程存在，则写出表达式；若不存在，则说明理由．

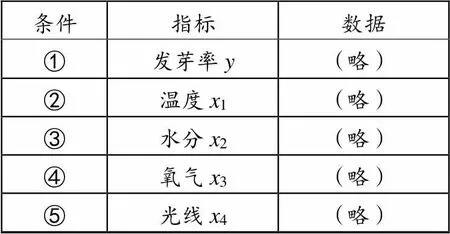
条件指标数据 ①发芽率y（略） ②温度x1（略） ③水分x2（略） ④氧气x3（略） ⑤光线x4（略）

问题：写出研究种子发芽率效果最好的回归方程．

该题重在考查学生能否选取合适的指标变量，构造理论回归模型．发芽率为因变量，如果所选自变量的取值不变，则不能建立回归模型．也可以给出4张图：

① 发芽率与温度1的散点图（略），

② 发芽率与水分2的散点图（略），

③ 发芽率与氧气3的散点图（略），

④发芽率与光线4的散点图（略）．

让学生任选一个条件，写出研究种子发芽率的回归方程．散点图中可能存在相关关系不明显的情况，考查学生能否从散点图中捕捉到合适的函数关系．该题借鉴了2020年新高考全国Ⅰ卷第17题的命题手法，属于条件不足情况．

“数学建模”核心素养水平二要求，“能够运用数学语言，表述数学建模过程中的问题以及解决问题的过程和结果，形成研究报告，展示研究成果”[1]．但数学考试中考查研究报告难度大，考虑在附加题、选做题中尝试．

变式7 改为解答题．（开放式）

给出真实的包含某作物种子发芽率的学生实验报告，记录了未加工的信息和数据，存在多余的信息和用不上的数据，属于条件冗余的结构不良问题．仿照语文“话题作文”模式，由学生自主发现问题、提出问题、建立模型、求解模型、检验结果、最终解决实际问题，并按数学建模的基本过程写成结构式论文，形成研究报告．

这样能让学生经历较完整的数学建模过程，即从数学的角度发现、提出问题，分析、解决问题，还能综合考查假设的合理性、建模的创造性、结果的正确性和表述的清晰性．但也带来了新问题，如学生答题时间增加、阅卷难度增大、是否适合纳入封闭式考场考试、未考查到学生自主收集数据等．

题型的灵活改编，能通过考查角度的改变，从封闭式问题过渡到开放式问题；也能通过题干条件的增减，从结构良好问题过渡到结构不良问题．并且这种改编是可逆的，见图5．

图5 “数学建模”核心素养纵向命题探索：题型灵活性

4.1.2 阶段差异性

数学建模活动是对现实问题进行数学抽象，用数学语言表达问题、用数学方法构建模型解决问题的过程[1]．针对同一个问题，往下游方向可推进问题的解决，往上游方向可回溯问题的源头．以案例1建立回归模型的一般过程为例，通过移动建模阶段，能改编出新的试题，见图6．

图6 “数学建模”核心素养纵向命题探索

案例1还未建立模型，重在通过观察图形趋势来构造理论模型，但无需求解模型，主要处于问题分析阶段，属于上游．需要说明的是，图6用虚线划分的界限并非泾渭分明．变式1、变式2、变式3、变式6、变式7仍处于上游，但由于在上游的具体位置存在差异，且考查的综合程度不同，和案例1相比难度均发生了变化．

变式1重点考查学生能否忽略次要因素、找准主要因素，而从给出合理的假设．变式1可以看作是案例1往上游方向回溯得到的子题，并且跳过了收集整理数据、设置指标变量这两个相邻的建模环节，这种改编方法可以称为跳跃回溯．反之，案例1可以看作变式1往下游方向推进得到，也跳过了相邻的建模环节，这种改编方法可以称为跳跃推进，见图7．

图7 回溯与推进示意图

变式2考查设置指标变量环节，可由案例1跳跃回溯得到，同时也是变式1往下游方向自然顺延的结果，于是变式2也可以由变式1改编得到，这种改编方法可以称为连续推进，反之，变式2连续回溯可以改编成变式1，见图7．变式3、变式6与案例1相比没有改变建模阶段；变式7将案例1跳跃回溯到了实际情境环节，解决过程跨越上中下游3个阶段，更确切地说，这是一道中上游问题．

变式4还未建立模型，主要处于模型求解阶段，属于中游，可以看作是案例1的连续推进．变式5已经建立模型，主要处于模型应用阶段，属于下游，可以看作是案例1的跳跃推进．

处于任意阶段的母题，都可以回溯或推进到其它阶段，形成子题，往上游回溯时，还能够将应用题回译成数学建模问题[21]．建模阶段的微调与题型的灵活变化，可以有效调节试题难度．

4.2 背景丰富性与模型广泛性相结合以实现素养综合性

探索横向命题时，暂不讨论纵向的变化．

4.2.1 背景丰富性

在命题中，选择合适的问题情境是考查数学学科核心素养的重要载体[1]．创设新情境能显著增加背景丰富性．从学生的角度可以把问题情境分为熟悉情境和陌生情境，改编试题时，可将母题迁移到关联情境或其它情境．关联情境与其它情境仅相对于母题而言，既有可能是熟悉情境，也有可能是陌生情境，见图8．

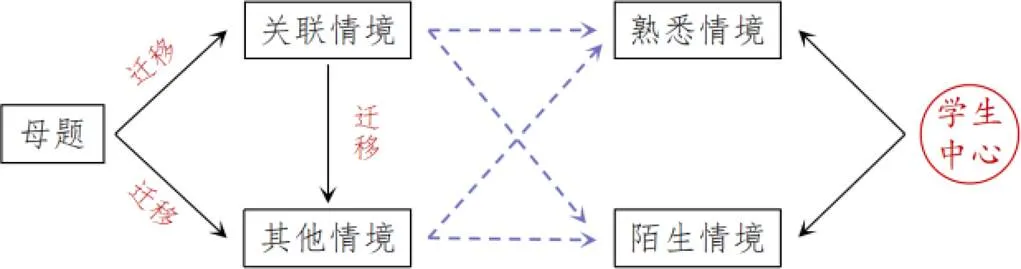
图8 “数学建模”核心素养横向命题探索

将案例1迁移到关联情境，可以形成新的变式子题．

变式8 改为火龙果种子发芽率问题．（关联情境）

红皮红肉、红皮白肉及黄皮白肉火龙果均具有较高的经济价值，某科研团队为研究这3种火龙果的萌芽差异进行了发芽实验，记录了14天的发芽数据，并将种子发芽率和时间（单位：天）整理得到下图[22]：

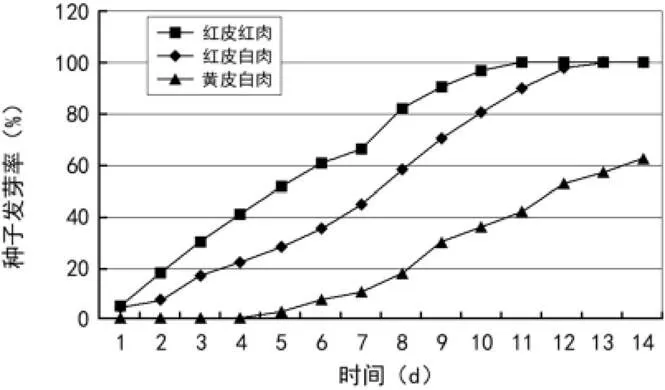
下面4个回归方程类型中最适宜作为红皮红肉火龙果种子发芽率和时间的回归方程类型是（ ）

A．=+B．=+2

C．=+eD．=+ln

变式9 改为火龙果幼苗种类判别问题．（关联情境）

某科研团队在研究火龙果幼苗形态实验中发现，红皮红肉、红皮白肉及黄皮白肉3种火龙果幼苗移栽后第60天，幼苗鲜重（单位：mg）、幼苗长度（单位：mm）、根总长度（单位：mm）存在显著差异[22]，其均值可构成幼苗形态3维坐标(1,1,1)、(2,2,2)、(3,3,3)（数据略）．现有一株同批次的火龙果幼苗不慎遗落了品种标签，测得其幼苗形态3维坐标为(,,)（数据略），请你合理判断此幼苗最有可能是这3种火龙果中的哪一种．

除了对熟悉情境迁移再利用，还可以将原问题推广到其它情境，“以陌生情境打造问题空间”实现背景创新[9]．

变式10 改为最优退休年龄问题．（其它情境）

延迟退休政策对于维持我国现收现付制统筹账户的平衡有着重要的作用，有学者研究发现，最优退休年龄与预期寿命、经济增长速度、入职年龄正相关，且受预期寿命影响最大[23]．现忽略其它因素，根据下表数据[23]：

预期寿命73.6476.3478.0079.4380.00 最优退休年龄59.6762.3363.9765.3865.94

仅考虑预期寿命与最优退休年龄的关系，最适宜的回归方程类型为（ ）

A．=+B．=+2

C．=+eD．=+ln

变式11 改为公共图书馆超效率得分问题．（其它情境）

有学者利用我国31个省份公共图书馆数据，分析公共图书馆投入产出效率．研究发现，地区人口规模1、地区经济发展水平2、地区居民收入水平3、地区居民高等教育程度4对公共图书馆效率都有正向的作用，并建立了关于公共图书馆超效率得分的回归模型[24]：

=0.0890+0.01471+0.04872+0.13203+0.01404．

已知A省与B省2020年的人口规模、经济发展水平、居民收入水平和居民高等教育程度情况（数据略），试比较这两个省份2020年的公共图书馆超效率得分．

向关联情境迁移时，可以由校外向校内迁移，如2019年北京卷理科第17题便对2018年全国Ⅲ卷理科第8题的情境进行了迁移，从“某群体成员移动支付使用情况”迁移到了“学生两种移动支付方式使用情况”；也可以由校内向校外迁移，如变式8、变式9；还可以向对立面迁移，如垃圾分类宣传（2020年全国Ⅱ卷理科第14题），反过来从数据上说明垃圾不分类所造成的环境污染和资源浪费情况，能获得新问题．向其它情境迁移时，可以对已有研究成果进行改编，如变式10、变式11；也可以把社会时事作为命题素材，如延迟退休政策（变式10）、2020年第七次全国人口普查等．不同的背景能够产生同一类问题，同一个背景可以产生不同的问题，由此形成包罗万象的实际背景，可以开阔学生视野．

4.2.2 模型广泛性

数学具有高度的抽象性，因而解决问题的关键，既不在于题型的多变，也不在于建模阶段的不同，更不在于问题背景的千差万别，而在于学生是否深刻掌握试题所考查的数学知识、透彻理解其中的思想方法，才能以不变应万变，即“注重数学本质、通性通法，淡化解题技巧”[1]，也即高考评价体系的“关键能力、必备知识”考查目标．

变式8、变式10、变式11与案例1相比，虽然问题背景各不相同，本质上却仍是在考查回归模型．变式11中的多元线性回归模型对学生来说较为陌生，但读懂题意后，只需代值计算比较大小，可以看作是比较三元一次多项式的值．变式9与变式8改编自同一背景，但考查角度不同导致所用的数学方法也不同，变式9考查了空间几何中两点间的距离公式，以及应用统计初步，可归为几何模型．

“数学建模”核心素养水平二要求，“能够选择合适的数学模型表达所要解决的数学问题”[1]．数学方法的选取依托于对现实问题考查的目的，高考中涉及的数学模型主要是学生运用所学知识能够建立并求解的初等模型，但也出现过学生还无法建立的模型，如Logistic模型．高考数学中来自科研成果简化的试题，拓宽了数学模型的广度，可以让学生深刻地“接触”到数学的应用，见识研究人员是怎么用数学的，从而心生向往，学习科学家那样“数学地思维”，这也是科研成果反哺教学一线的一种形式．因此，值得向学生大力引介经典模型，尤其是学者在各领域科研中常用到的数学模型，以及在解决新问题时改进后的模型．对于其中简单的模型，可以全面考查建模与求解过程，如变式8、变式9、变式10；复杂的模型，可以在介绍完背景后直接给出模型，降低难度，从模型应用或模型性质分析等其它角度进行考查，如变式11．

不同问题背景与数学模型，自带不同的核心素养．例如几何问题在考查“数学建模”核心素养的同时，往往也能考查“直观想象”核心素养，而统计模型能自然兼顾“数据分析”核心素养．在同一道试题中，增加知识点，能同时加强知识和素养考查的综合性．比如2021年新高考Ⅱ卷第21题，在概率统计模型中设计了方程最小正实根的判别．试题的综合性越强，能考查到的核心素养也会越多．

综上，横向的变化扩大了数学的应用领域，纵向的变化让数学的考查变得灵动起来．命题时，从横向上，可以先确定问题背景及题目立意，再寻求恰当的数学方法，也可以先确定数学模型，再选取合适的现实背景；从纵向上，可以根据考查目的先确定具体的建模阶段，再考虑所设问题与不同题型的适配度，并灵活调整．为实现“数学建模”核心素养命题多样性，从这两个方向进行改编，能由母题衍生出众多子题．对于前文给定的一道母题——案例1，变式1至变式7是纵向衍生的子题，变式8、变式10是横向衍生的子题，变式9、变式11是纵横交错衍生的子题．

5 反思总结

前面分析了近6年高考真题，从“数学建模”核心素养命题多样性角度进行了探索，分别从纵向和横向给出了命题建议，以母题为原点，纵横交错，寓生动数学于精彩世界．更进一步，可以参考学科核心素养评价框架[25]和改进后的双向细目表[26]，对每道题定位并注明标签，形成试题库．组卷前，既需要从宏观层面考虑各知识点、核心素养、题型等内容的比例分配，整套试卷的难易程度，适合的题目序号；也需要从微观层面打磨题目的科学性、精炼性、创新性、公平性．为提高数学命题质量，还可以博采众长，从国外试题的命题技术[7，18]中汲取灵感，并采取科学的评价方法[27–44]．

“数学建模”核心素养的独特性，使一道好题目能够有利于启示学生用数学眼光观察世界，有利于启迪学生用数学思维思考世界，有利于启发学生用数学语言表达世界；同时还具有良好的教学价值、科研价值、育人价值．“教育意味着一棵树摇动另一棵树，一朵云推动另一朵云，一个灵魂唤醒另一个灵魂．”正是命题人先在数学世界里关注着现实应用、在纷繁现象里洞察出数学本质，并期许学生能通过数学看到精彩世界、透过现象感知生动数学，在摇动、推动与唤醒中，呈现出了“培根铸魂、启智润心”的好题目．而这也是“数学建模”核心素养试题承担的使命．

数学教育作为一个跨学科领域，理应以跨学科视角进行研究，例如，从社会文化视角研究数学建模教学的社会性．社会性是教学的根本属性[39]，数学建模教学是一种浸染在社会情境中的集体性活动，数学模型的建构也是在社会活动中完成的．过去一味强调数学模型的构造或许是数学建模教学难以深化的重要原因，相较于数学模型的构造来说，数学建模最为关键的环节是将真实问题转化为数学问题．从教学的社会性来看，诠释学生数学建模的过程化表现是未来数学建模教学研究的应然方向．从社会文化视角分析数学建模教学中，学生理解情境、提出假设、识别变量、建立模型、论证方案等环节的表现与问题，探讨数学建模中学生话语互动呈现的特征以及这些特征是如何促进学生完成数学建模任务的．同时，课程是教学社会性的内隐表达，课程与教学的社会互动关系决定着教师对课程的解读和学生对课程的理解．例如，数学教科书中呈现的真实性问题，需要经过教师和学生的改造或意义添加后，才可以转化成数学建模问题，这就需要从社会文化视角探讨教师和学生使用教科书的过程，教师对课程内容的选择与加工为学生提供了很好的数学建模学习机会．

[1] 中华人民共和国教育部．普通高中数学课程标准（2017年版2020年修订）[M]．北京：人民教育出版社，2020：1．

[2] 李作滨．素养导向的数学测评研究——以2018年高考为例[J]．数学教育学报，2018，27（6）：33–37．

[3] 俞梦飞，章飞．核心素养视角下数学高考试卷评价研究——以2018和2019年江苏高考卷为例[J]．数学教育学报，2020，29（2）：35–40．

[4] 覃创，严忠权．核心素养为导向的数学测评研究——以2019年高考全国Ⅲ卷为例[J]．数学教育学报，2020，29（2）：24–28．

[5] 李华，胡典顺．基于数学核心素养评价框架的试卷测评研究——以2019年高考全国卷为例[J]．数学教育学报，2020，29（2）：18–23．

[6] 覃创，严忠权，李敏．落实素养为本的高考测评研究——以2020年全国I卷数学为例[J]．数学教育学报，2020，29（6）：21–24．

[7] 张玉环，周侠，陈爽．核心素养视角下中法高考数学试题的比较研究——基于2015—2020年中国和法国高考数学试卷[J]．数学教育学报，2021，30（1）：42–48，73．

[8] 陈昂，任子朝．数学高考中实践应用能力考查研究[J]．数学教育学报，2017，26（3）：15–18．

[9] 李健，童莉．高考评价体系中“应用性”与“创新性”要求——基于2020年高考数学试卷中问题情境的分析[J]．基础教育课程，2020（Z2）：18–22．

[10] 王雅琪，汪燕铭，曹辰．基于学科能力视角的高考数学北京卷命题研究[J]．中国考试，2019（10）：53–58．

[11] 倪黎，茹凯，安黔江．问题驱动下的高中数学建模教学探究——以2018年高考数学全国卷Ⅱ理科第18题为例[J]．数学通报，2020，59（8）：46–49，62．

[12] 张定强，裴阳．探析建模思想落实核心素养——近五年高考数学建模思想考查的特征分析及启示[J]．考试研究，2018（6）：85–90．

[13] 张彬．基于“数学建模”素养的2019年高考数学试题分析[J]．数学教学研究，2020，39（2）：49–53．

[14] 姜钢．探索构建高考评价体系，全方位推进高考内容改革[N]．中国教育报，2016–10–11（3）．

[15] 姜启源，谢金星，叶俊．数学模型[M]．5版．北京：高等教育出版社，2018：1．

[16] 张淑梅，何雅涵，保继光．高中数学核心素养的统计分析[J]．课程·教材·教法，2017，37（10）：50–55．

[17] 黄健，鲁小莉，王鸯雨，等．20世纪以来中国数学课程标准中数学建模内涵的发展[J]．数学教育学报，2019，28（3）：18–23，41．

[18] 廖运章，王华娇．英国数学英才选拔考试MAT命题技术分析[J]．数学教育学报，2016，25（3）：34–37，102．

[19] 新华社．中共中央国务院印发《深化新时代教育评价改革总体方案》[EB/OL].（2020–10–13）[2021–07–03]. http:// www.gov.cn/gongbao/content/2020/content_5554488.htm.

[20] 任子朝，赵轩．数学考试中的结构不良问题研究[J]．数学通报，2020，59（2）：1–3．

[21] 黄英芬，颜宝平，龙红兰．从应用题到建模问题的回译——一种开发数学建模素材的新思路[J]．数学通报，2019，58（9）：34–37．

[22] 葛宇，丁哲利，程志号，等．3种火龙果种子萌发及其幼苗形态的比较研究[J]．种子，2017，36（7）：22–24．

[23] 高彦，赵君彦，曹园．不同寿命下最优退休年龄的测算[J]．统计与决策，2021，37（2）：75–79．

[24] 张伟锋，宋红文，覃红．公共图书馆投入产出效率及影响因素研究[J]．数理统计与管理，2019，38（6）：1 080–1 092．

[25] 喻平．数学核心素养评价的一个框架[J]．数学教育学报，2017，26（2）：19–23，59．

[26] 喻平．基于核心素养的高中数学课程目标与学业评价[J]．课程·教材·教法，2018，38（1）：80–85．

[27] 柯跃海，陈清华．高考数学命题质量评价的基础与方法[J]．数学教育学报，2020，29（1）：48–51．

[28] 任子朝，赵轩，关丹丹，等．图形分析法在高考试题评价中的应用研究[J]．数学教育学报，2021，30（1）：37-41．

[29] 史宁中，吕世虎，李淑文．改革开放四十年来中国中学数学课程发展的历程及特点分析[J]．数学教育学报，2021，30（1）：1-11．

[30] 赵思林，潘超．中学数学教师核心素养及构成要素[J]．数学教育学报，2021，30（2）：48-54．

[31] 陆珺，胡晴颖．论数学解题教学的教学[J]．数学教育学报，2021，30（2）：55-60．

[32] 路江江，王亚妮．高中数学教育中如何培养学生的数学核心素养——王尚志教授访谈录[J]．数学教育学报，2021，30（2）：67-70．

[33] 伍春兰．PDSA视域下基于教师学习的中学数学课例研修研究[J]．数学教育学报，2021，30（3）：78-82．

[34] 栗小妮，汪晓勤．HPM课例研究对教师MKT的影响[J]．数学教育学报，2021，30（3）：83-89．

[35] 黄荣金，曹一鸣．中国数学教师合作学习的理论和实践：一个国际视角的审视[J]．数学教育学报，2021，30（3）：1-3．

[36] 丁莉萍．数学教师合作学习的理论与实践之比较分析[J]．数学教育学报，2021，30（3）：4-11．

[37] 喻平，董林伟，郭庆松．中学生数学品格与价值观的问卷设计[J]．数学教育学报，2021，30（4）：12-18．

[38] 吕松涛，曹广福．高中向量教学中数学思想的渗透[J]．数学教育学报，2021，30（4）：19-24．

[39] 武丽莎，朱立明．高中数学学科核心素养：生成机制与培养路径[J]．数学教育学报，2021，30（4）：25-29．

[40] 王海青，曹广福．从《原本》谈中学平面几何课题式教学研究[J]．数学教育学报，2021，30（5）：39–46．

[41] 崔志翔，杨作东．义务教育阶段一个数学核心素养的评价框架[J]．数学教育学报，2021，30（5）：47–52．

[42] 姜文，严虹，夏小刚，等．高中生数学学习态度的调查研究——基于贵州省的调查数据分析[J]．数学教育学报，2021，30（5）：53–57．

[43] 尚亚明，熊斌．数学问题提出的过程性研究述评[J]．数学教育学报，2021，30（5）：66–71．

[44] 唐海军，严虹，任旭．数学合作问题解决视野下的“三教”探析[J]．数学教育学报，2021，30（5）：72–79．

Test Analysis and Proposition Exploration of “Mathematical Modeling” Core Literacy

NI Li, RU Kai, YAN Bao-ping

(School of Data Science, Tongren University, Guizhou Tongren 554300, China)

The “mathematical modeling” literacy test is relatively weak in the evaluation of the core literacy of mathematics in the college entrance examination. Using the case analysis method, this paper systematically analyzes the test questions of the core literacy of “mathematical modeling” in the 2016––2021 college entrance examination mathematics papers from six perspectives: score characteristics, question type characteristics, background characteristics, model characteristics, literacy characteristics, and stage characteristics. Finally, this paper proposes that the diversity of propositions should be explored from vertical (level of difficulty) and horizontal (comprehensive literacy) directions. The results show that: in the proposition of the college entrance examination, attention should be paid to “the combination of the flexibility of the question types and the difference of the stages to change the level of difficulty; the combination of the richness of background and the extensiveness of the model to realize the comprehensiveness of literacy”.

mathematical modeling; core literacy; test analysis; proposition; case analysis

2021–11–19

2021年贵州省教育科学规划课题——核心素养视阈下我国西部地区初中数学建模教学的理论逻辑和实践路径研究（2021B166）；贵州省区域一流建设培育学科——教育学（黔教科研发〔2017〕85号）；2016年贵州省本科教学工程项目——卓越数学教师培养计划（2016SJZYRC001）

倪黎（1989—），女，贵州松桃人，副教授，硕士，主要从事数学教育研究．茹凯为本文通讯作者．

G632.4

A

1004–9894（2022）02–0069–08

倪黎，茹凯，颜宝平．“数学建模”核心素养试题分析与命题探索[J]．数学教育学报，2022，31（2）：69-76．

[责任编校：陈汉君、张楠]