中国中学生数学学习策略运用的元分析

何木叶，寇冬泉，刘电芝，江茂欣

中国中学生数学学习策略运用的元分析

何木叶1，寇冬泉2，刘电芝1，江茂欣1

（1．苏州大学 教育学院，江苏 苏州 215123；2．扬州大学 教育科学学院，江苏 扬州 225002）

元分析指对来自各个研究的大量分析结果的统计分析，目的是整合研究结果．采用元分析技术考察中国中学生数学学习策略的运用状况及其与数学成绩的关系．结果显示：年代对数学学习策略调节效应不显著．中学生数学学习策略运用随年级升高呈轻微下降趋势．地域和性别对数学学习策略调节效应至高中阶段浮现，欠发达地区高中生数学认知策略显著低于发达地区．数学认知策略和数学成绩相关最高．这提示中学生数学学习策略发展趋势不甚理想，要重视高中阶段数学学习策略教学，可考虑将数学认知策略作为教学重点．

中学生；数学学习；学习策略；元分析

1 问题提出

数学是基础教育阶段的核心课程，在促进学生的智力发展中起着举足轻重的作用．数学学习策略指“一切有助于数学学习，包括对概念、公式的理解、记忆、运用及数学问题解决的学习策略”[1]，是数学自主学习必不可少的工具．数学学习策略“可以部分克服对数学学习的焦虑”[2]，还“与数学学业水平呈显著正相关”[3]．中学数学难度较小学有较大提升，提升中学生的数学学习策略有助于增强学生学好数学的自信心，发展自主学习的能力．对数学学习策略运用状况和特征的系统分析是数学学习策略培育的基础，可以为数学学习策略的教学或指导提供参考．

中国中学数学学习策略运用研究起步于20世纪90年代，这一时期的研究较为零散．21世纪初，在新课程改革倡导将“过程与方法”纳入三大教学目标之一的背景下，数学学习策略的运用研究随之增多．主要包括两个领域．第一，数学学习策略调查问卷编制．代表性问卷有莫秀锋、刘电芝编制的“初中生数学学习策略量表”[4]，王光明、刘丹编制的“初中生数学学习策略调查问卷”[5]，王光明等编制的“高中生数学学习策略调查问卷”[6]．莫秀锋等和王光明等编制的数学学习策略测量工具都包括数学认知策略、数学元认知策略和数学资源管理策略三维度[4–5]．莫秀锋等认为数学认知策略包括通用认知策略和具体认知策略[4]．王光明等则认为数学认知策略包括复述、精加工和组织三策略[5]．莫秀锋等和王光明等均认为数学元认知策略包括计划、监控、反思、调节四策略．数学资源管理策略均包括时间管理、环境管理、努力（心境）管理、合作求助（外界求助）四策略[4–5]．第二，数学学习策略运用状况分析．主要集中在人口统计学资料的特征分析、数学学习策略运用与成绩的相关研究，但部分研究结果存在矛盾．（1）年级差异：莫秀锋、刘电芝研究表明初中生数学学习策略呈逐年下降的趋势[1]，杨云苏的研究结果则截然相反[7]，杨琳琳和刘书玺关于高一和高二数学学习策略是否存在显著差异的研究结果亦存在分歧[8–9]．（2）性别差异：马超周和孔令先关于初中男女生数学认知策略和资源管理策略差异的研究结果大相径庭[10–11]，吴梦菲和高金金关于高中男女生数学认知策略是否存在显著差异的研究结果亦不同[12–13]．（3）数学学习策略与成绩的关系：吴现荣、宋军研究表明初中生数学认知策略和成绩相关最高[14]，陈方的研究则显示，初中生数学资源管理策略和成绩的相关性最高[15]，王国龙的研究表明高中生数学元认知策略和数学成绩相关最高[16]，刘书堃的研究结果则相反[9]．研究结果的分歧为教师基于人口统计学特征的策略教学和把握策略教学的重点带来困惑．中学生数学学习策略运用人口统计学特征的原貌可能是什么？哪种数学学习策略最能促进数学成绩？为什么研究者关于数学学习策略运用得出不同的结论？是否受到取样年、地域、测量工具等因素的影响？数学学习策略运用研究需要澄清不同研究结果的不一致．

元分析指“对来自各个研究的大量分析结果的统计分析，目的是整合研究结果”[17]，“可澄清及协助解决研究结果的不确定性或相互矛盾的情形”[18]．研究问题如下．

（1）中国中学生数学学习策略运用情况怎样？是否随年代、学段呈上升趋势？

（2）对于学习策略运用在人口统计学上的争议性问题，通过元分析可以得出什么结论？

（3）中学生数学学习策略运用的调查结果是否存在地域、测量工具的差异？

对以上问题的探讨将有助于进一步开展更科学的数学学习策略研究，为数学学习策略教学实践及辅导提供借鉴．

2 方法

2.1 文献检索

以“初中”或“高中”或“中学”“数学学习策略”或“数学认知策略”或“数学元认知策略”或“数学资源管理策略”为组合搜索词，在中国知网、维普期刊网以及万方数据库进行检索，以“Mathematics Learning Strategies”或“Mathematical Cognitive Strategy”或“Mathematical Meta- cognitive Strategy”或“Mathematical Resource Management Strategy”和“Chinese”或“China”等为组合搜索词在Wiley Online Library、Springer Link、Elsevier Science Direct、Web of Science、Education Resources Information Center数据库分别对基于中国样本的数学学习策略进行检索．文献检索时间是文献建库至2020年6月30日，共搜索到1 242篇文献．由于中国2000年之前的数学学习策略的调查数量较少、维度繁多，因此也纳入2001—2020年的文献进行元分析．

2.2 纳入与排除标准

纳入标准：

（1）研究对象是中国的中学生；

（2）研究内容是数学学习策略；

（3）研究类型是问卷调查研究；

（4）研究工具子维度包括：数学认知策略、数学元认知策略或数学资源管理策略，研究工具低风险（由中国研究者开发且总量表Cronbach’s系数≥0.7，引用的是在中国人样本中具有信效度的量表[19]）；

（5）统一使用李克特5级计分；

（6）研究至少报告了数学学习策略一个维度的平均数、标准差、样本量；

（7）数据重复发表的只取较早发表的研究．

排除标准：

（1）非中国样本的中学生；

（2）特殊对象，如只报告学优生或学困生数据的文献；

（3）单一数学学习策略，例如，数学概念学习策略、合作学习策略等；

（4）非问卷调查研究，例如，综述、思辨研究等；

（5）测量工具高风险（①量表由中国研究者开发但是没有报告测量学特征，②总量表Cronbach’s系数<0.7或未说明是否适用于中国样本的量表[19]）；

（6）测量工具非李克特5级计分；

（7）无法提取效果量的文献；

（8）数据出现明显错误或与文中相关表述矛盾的文献．

依据以上标准，共纳入符合标准的文献29篇（如表1所示）．总样本量为14 570人，涉及22个省及直辖市．初中生的总样本量8 200人，最小样本量为43人，最大样本量为2 032人，平均样本量为631人．高中生的总样本量为6 370人，最小样本量为93人，最大样本量为919人，平均样本量为354人．

2.3 数据提取与转化

提取文献特征：作者、出版年、测量工具、样本量、被试类型（地域、学段、年级、性别）．提取结果变量：数学认知策略、数学元认知策略、数学资源管理策略及其与成绩的相关．如果某研究数据出现在两篇（如分别出现在期刊和学位论文中）及两篇以上文献中，参照张书朋[38]等研究将含有更充分信息的文献纳入此次元分析．对只报告了性别、年级等群组数据而未报告总体数据的文献，分别对群组平均数和标准差加权合成获得总体均值和标准差．

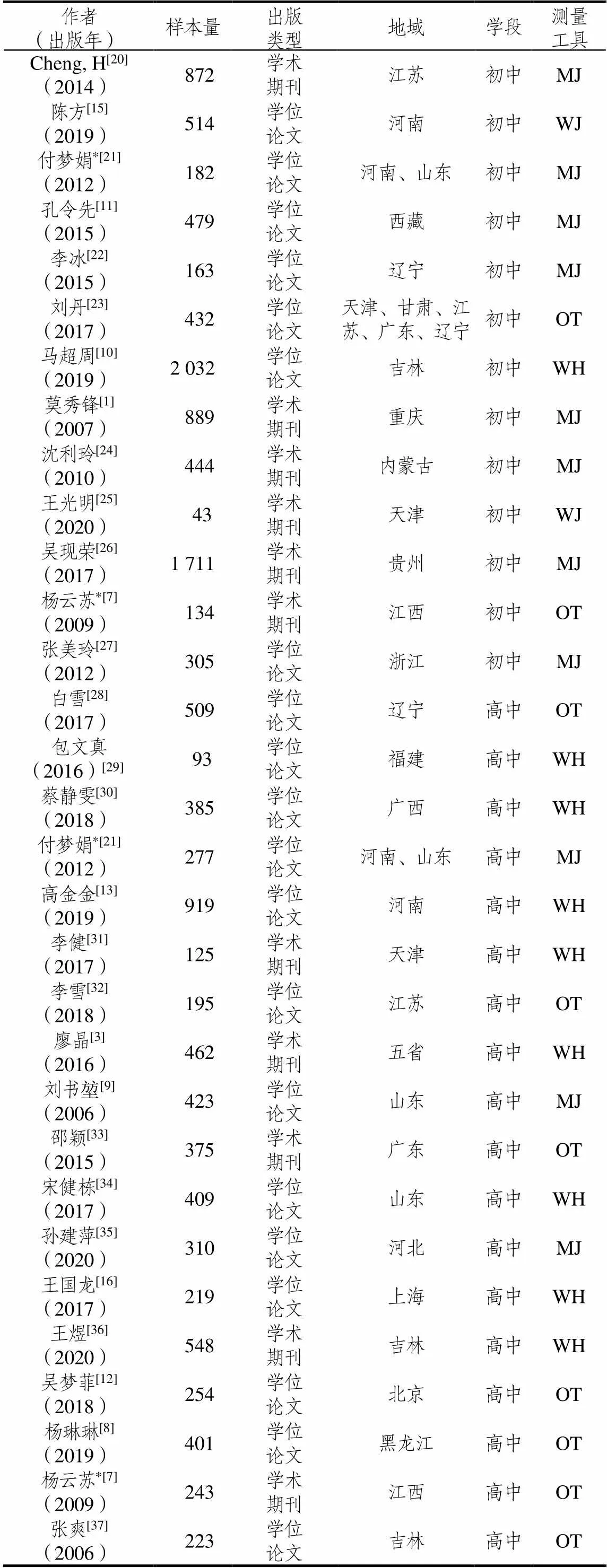
表1 纳入文献基本信息

注：*指一篇文章同时调查了初中生和高中生的数学学习策略，根据学段分开纳入数据．MJ代表采用或基于莫秀锋等的“初中生数学学习策略量表”修订、编制的测量工具．WJ代表采用或基于王光明等的“初中生数学学习策略调查问卷”修订、编制的测量工具．WH代表采用或基于王光明等的“高中生数学学习策略调查问卷”修订、编制的测量工具．OT代表其它自编量表和引用其他研究者的测量工具．

2.4 编码

（1）学段．编码为初中、高中．（2）地域．根据世界银行高收入国家人均GDP1.2万美元的标准和国家统计局发布的2008—2018年人均GDP数据测算的结果[39]，将北京、上海、天津、江苏、浙江、广东和福建等7省份编码为发达地区，其它省份编码为欠发达地区．（3）测量工具．将采用或基于莫秀锋等的“初中生数学学习策略量表”修订、编制的测量工具编码为1；采用或基于王光明等的“初中生数学学习策略调查问卷”修订、编制的测量工具编码为2；采用或基于王光明等的“高中生数学学习策略调查问卷”修订、编制的测量工具编码为3；其它自编量表和引用其他研究者的测量工具编码为4．由两位研究者根据编码标准独立编码，Kappa值为0.954，编码一致性非常好．对不一致的地方由两位编码者通过交叉核验，协商一致确定最终编码．

2.5 比较标准的确定

采用王光明等天津市初中生数学学习策略水平常模[25]作为初中常模（简称为JJ常模），共1 288份有效样本．采用李健等天津市高中生数学学习策略水平的常模[31]作为高中常模（简称为JH常模），共1 026份有效样本．介于JJ常模和JH常模是区域性常模，不能代表全国水平．因而萃取的数据和JJ常模或JH常模的比较仅用于了解中学生数学学习策略大概水平．此外，由于JJ常模和JH常模是发达地区常模，将其作为发达地区的代表和欠发达地区进行比较．

2.6 统计分析

采用Endnote9.0、Excel2003和SPSS20.0进行文献查重、数据录入和编码、数据转化．采用CMA3.0进行异质性检验、效应值计算、调节效应分析和出版偏倚检验．分别以Cohen作为两组差异的效应值（小效应：0.2；中效应：0.5；大效应：0.8）；采用作为相关效应值（小效应：0.1；中效应：0.3；大效应：0.5）[40]．

3 结果

3.1 中学生数学学习策略运用状况

初中生和高中生数学认知策略、数学元认知策略、数学资源管理策略的检验<0.001，2>75%，见表2．这说明研究之间存在高度异质性．异质性主要来自研究之间的真实差异，因而选择随机效应模型，以纳入组间和组内误差．

初中生数学认知策略、数学元认知策略和数学资源管理策略和JJ常模差异未达到统计学意义．高中生数学认知策略、数学资源管理策略显著低于JH常模（<0.05），效应量（=–0.30，–0.23）的绝对值为小效应，见表2．

表2 中学生数学学习策略运用现状

注：全部选用随机效应，代表原始研究的数目，、2、P代表异质性检验统计量，代表效应值，95%为结果变量所对应的效果量的95%的置信区间，P代表效应值显著性检验的统计值，以下同．

3.2 中学生数学学习策略运用的调节效应分析

3.2.1 年代

以年代为自变量，初中或高中生数学认知策略、数学元认知策略和数学资源管理策略与常模的差异值为因变量进行元回归分析．年代对初中生和高中生数学认知策略、数学元认知策略、数学资源管理策略调节效应均不显著（初中：Coefficient=0.01，–0.01，0.00；=0.572，0.493，0.963；高中：Coefficient=0.00，0.00，0.03；=0.974，0.788，0.369）．

3.2.2 人口统计学因素

与发达地区的常模相比，欠发达地区初中生的数学认知策略、数学元认知策略、数学资源管理策略差异不显著（>0.05）．欠发达地区高中生的数学认知策略显著低于发达地区的常模（<0.05），效应量（=–0.42）的绝对值接近中效应．欠发达地区高中生数学资源管理策略显著低于发达地区的常模（<0.05），效应量（=–0.24）的绝对值为小效应，见表3．

中学生数学学习策略呈下降趋势．数学认知策略、数学资源管理策略初一显著高于初二（<0.05），初二显著高于初三（<0.05），初二数学元认知策略高于初三（0.05<< 0.07），以上效应均为小效应，见表3．高一数学认知策略、数学元认知策略、数学资源管理策略高于高二（<0.05），以上效应值均为小效应．高二和高三数学认知策略、数学元认知策略、数学资源管理策略差异不显著（>0.05），见表3．

初中男女生的数学认知策略、数学元认知策略、数学资源管理策略差异均不显著（>0.05）．高中男生的数学认知策略和数学元认知策略高于女生（<0.05），但男女生之间差异的效应值均很小，见表3．

3.2.3 测量工具

为保证元分析结果的相对准确和稳定，若调节变量的各分类中纳入的研究数量不足2篇，在考察调节作用时不计入分析．MJ、WJ、QT对初中生数学认知策略、数学元认知策略、数学资源管理策略调节效应不显著（=0.20，=0.906；=0.11，=0.946；=3.49，=0.175）．MJ、WH、QT对高中生数学认知策略、数学元认知策略、数学资源管理策略调节效应不显著（=0.66，=0.720；=0.33，=0.848；=0.64，=0.727）．

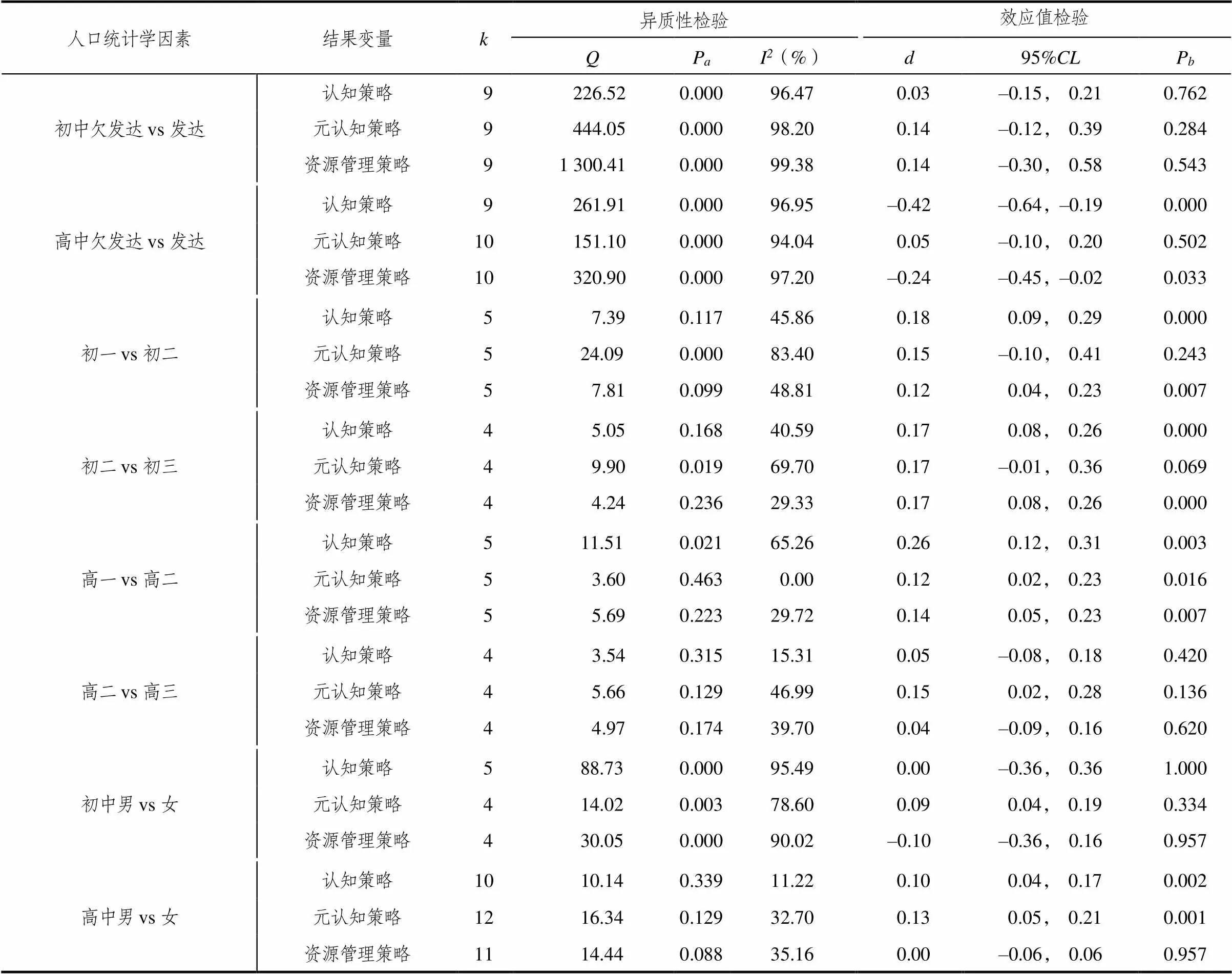
表3 数学学习策略人口统计学因素调节效应分析

注：<0.01，2≥50%（中等以上异质）采用随机效应模型，>0.01，2<50%（中等以下异质性）采用固定效应模型，以下同．

3.3 数学学习策略与数学学习成绩的相关

中学生数学认知策略、数学元认知策略、数学资源管理策略与数学成绩均呈显著相关．除高中数学元认知策略和资源管理策略外，其它数学学习策略与成绩的相关均达到中效应．初中数学学习策略各维度和成绩相关效应量大小为数学认知策略>数学元认知策略>数学资源管理策略．高中数学学习策略各维度和成绩相关效应量大小为数学认知策略>数学资源管理策略>数学元认知策略，见表4．

表4 数学学习策略和学习成绩的关系

注：代表数学学习策略和成绩相关的效应值．

3.4 出版偏倚检验

失效安全系数N和’线性回归检验显示：中学生数学认知策略、数学元认知策略、数学资源管理策略均表现出N>5+10（为原始研究的数目），’检验，>0.05．这表明：中学生数学学习策略的运用调查不存在出版偏倚，如表5所示．

表5 出版偏倚检验

4 讨论

4.1 中国中学生数学学习策略发展趋势不甚理想

元分析发现年代对中国中学生数学学习策略的调节效应不显著，数学学习策略运用随年级上升有所下降．这表明中国中学生数学学习策略运用状况不容乐观．可能原因为：其一，课改倡导并未根本改变数学课堂中以知识传授为主的教学传统．2001年《基础教育课程改革纲要（试行）》明确提出，“要使学生具有适应终身学习的基础知识、基本技能和方法”“改变课程过于注重知识传授的倾向……使获得基础知识与基本技能的过程同时成为学会学习的过程”[41]．但相关研究发现，“数学教师被动地适应新形势，教师在课程理论或反映当今时代的先进教育理论中没有坚实的基础……即使接受了新的理念，也无能力和缺乏时间、精力践行理念”[42]．“教师天天要求学生背公式、定律，却不教他们记忆的方法；学生解题遇到困难，教师也很少从学生的解题思路上分析原因”[43]，“绝大多数教师习惯教知识，缺乏教策略的意识”[44]，“也不知道如何进行策略教学”[45]．其二，随年级逐增的课业压力可能使中学生数学学习策略运用受限．“随着中学生年级的逐渐升高，学生的学习任务和考试压力不断增加，教师课堂教学内容也相应增多，学生自己安排学习活动的自由度减小．”[46]这在一定程度导致学生实际使用学习策略的频率变少了．“伴随着繁重课业，机械反复练习大量增加，学生已从动脑筋思考变成为自动化反应，学习策略和学习内容产生了消极的固化练习”[45]，进而影响到学习策略的运用．

需要指出的是，尽管元分析发现随年级升高数学学习策略下降的效应值较小，但如果对这种轻微下降的趋势未引起足够重视的话，长此以往，可能不利于学生数学自主学习能力的发展．如何将理念转变为行动应成为数学教育甚至基础教育研究的重点．

4.2 数学学习策略的地区和性别差异在高中阶段浮现

经济欠发达地区初中生数学学习策略总分和发达地区常模的差异不显著．经济欠发达地区高中生数学认知策略、数学资源管理策略显著低于的发达地区常模，其中数学认知策略的经济区域差异接近中效应．这与马郑豫、张家军等研究发现的通用学习策略存在地域差异[47]有一致之处．这在一定程度折射出高中数学学习策略教育水平的经济区域差异．庞祯敬、李慧发现“区域间普通高中教育发展水平差异巨大，两极分化现象严重”[48]．不同经济区域教师学历结构、教育理念、教育技术、教育方法等可能对高中阶段教学质量产生了一系列的影响，导致学习策略使用差异[47]．与初中阶段相比，经济发达和欠发达地区高中策略教学质量的差异会导致欠发达地区高中生数学学习策略低于发达地区．对于欠发达地区高中而言，需加强策略意识、提高数学学习策略教学质量，从而推动高中生数学学习策略的运用．

初中男女生数学学习策略差异不显著；高中男生的数学认知策略和数学元认知策略优于女生，但效应值较小．这说明数学认知策略和元认知策略的性别差异迟至高中阶段才显现，且差别较小．这与马郑豫、张家军对通用学习策略性别差异研究结论[47]不一致．通用学习策略和学科学习策略是否在性别上存在不同的差异有待进一步研究．

4.3 初中生和高中生数学学习策略与成绩的相关存在共性和差异

中国中学生数学学习策略绝大多数维度和成绩的相关达中效应，进一步说明数学学习策略在数学学习和教学中的重要性．初中生和高中生数学认知策略和成绩相关系数最高，这与Cheng等研究发现的“具体认知策略得分高的学生更有可能成为优秀生，基本认知策略可使学生避免成为后进生”[20]，以及Donker等研究发现的“认知策略中的精制策略能有效促进数学学习成绩”[49]有一致之处．初中生数学元认知策略和成绩呈中等水平相关，与Pintrich研究发现的“如果学生具有足够的动机使用元认知策略，就足以提高成绩”[50]一致．因而，在初中阶段应重视数学认知策略和数学元认知策略的教学，在高中阶段应进一步突出数学认知策略的教学．

4.4 不同测量工具未影响到研究结果的一致性

不同测量工具对中学生数学学习策略各维度调节效应不显著．原因可能是：其一，基于文献纳入标准，纳入的测量工具主要是基于迈克卡学习策略的分类，拥有相同的理论基础；其二，通过对MJ和WJ、WH的文本分析，发现莫秀锋等和王光明等对数学认知策略下的子策略命名不同，但题项反映的策略实质比较接近，两项研究的数学元认知策略和资源管理策略子维度反映的策略实质相似．

4.5 研究的可靠性

出版偏倚分析显示，中学生数学学习策略研究出版偏倚的可能性较小．这表明元分析结论具有一定的可靠性．

5 局限与展望

第一，近20年国内中学生数学学习策略运用的量化研究比较薄弱，这在一定程度上影响了纳入中学生数学学习策略元分析的原始研究数量，尤其是影响部分亚组研究的数量，进而可能会影响到研究结论的推广范围．

第二，国内中学生数学学习策略运用缺乏全国常模，导致无法在元分析中将近20年数据和全国常模比较．未来需要开展大规模的数学学习策略运用的调查，建立中学生数学学习策略运用的全国常模，以便进一步宏观把握中国中学生数学学习策略运用状况．

第三，数学学习策略研究间的高异质性意味着数学学习策略可能有多种的异质源．未来需要进一步开展数学学习策略异质源探究，以便更全面深入揭示数学学习策略的运用特征，为加强数学学习策略的针对性教学和指导提供参考．

6 结论

第一，近20年中国中学生数学学习策略运用无明显变化，并随年级上升呈轻微下降趋势．应重视将数学学习策略的教学理念转换为策略教学行动的探索．

第二，高中生数学认知策略与数学成绩呈显著中相关．欠发达地区高中生数学认知策略不甚理想．鉴于此，欠发达地区高中阶段需加强数学认知策略的教学．

第三，性别对初中生数学学习策略运用无调节效应，对高中生数学认知策略和元认知策略运用有较小的调节效应．这说明，男女生数学学习策略到高中阶段才出现轻微的分化．

[1] 莫秀锋，刘电芝．初中生数学学习策略的个体差异研究[J]．数学教育学报，2007，16（4）：56–58．

[2] MACHIDA K, CARLSON J S. Effects of a verbal mediation strategy on cognitive processes in mathematics learning [J]. Journal of Educational Psychology, 1984, 76 (6): 1 382–1 385.

[3] 廖晶，王光明，黄倩，等．高中生高效率数学学习策略特征及对数学学业水平的影响路径[J]．数学教育学报，2016，25（5）：61–66．

[4] 莫秀锋．初中生数学学习策略的发展特点及可控心理影响因素研究[D]．重庆：西南师范大学，2002：18–27．

[5] 王光明，刘丹．初中生数学学习策略调查问卷的设计与编制[J]．数学教育学报，2017，26（3）：19–24．

[6] 王光明，廖晶，黄倩，等．高中生数学学习策略调查问卷的编制[J]．数学教育学报，2015，24（5）：25–36．

[7] 杨云苏，昌庆煌．中学生数学学习策略及其相关实证研究[J]．井冈山学院学报，2009，30（5）：139–142．

[8] 杨琳琳．高中生数学学习策略应用现状的调查研究[D]．哈尔滨：哈尔滨师范大学，2019：16–34．

[9] 刘书堃．高中生数学学习归因、学习策略与数学学习成绩关系的研究[D]．济南：山东师范大学，2006：21–34．

[10] 马超周．数学学业情绪对数学学业成就的影响：数学自我效能和数学学习策略的中介效应分析[D]．长春：东北师范大学，2019：11–24．

[11] 孔令先．西藏中学生数学学习策略研究——以拉萨市初中生为例[D]．拉萨：西藏大学，2015：15–32．

[12] 吴梦菲．高中生坚毅性、学习策略与数学成绩的关系研究[D]．北京：中央民族大学，2019：14–46．

[13] 高金金．高中生数学学习策略表现及其影响因素研究——以开封市5所中学为例[D]．开封：河南大学，2019：13–32．

[14] 吴现荣，宋军．贵州南部地区水族初中生数学学习策略的调查分析[J]．数学通报，2017，56（7）：13–17．

[15] 陈方．初中生数学学习策略的发展及其与数学成绩关系研究[D]．开封：河南大学，2019：17–35．

[16] 王国龙．高中生运用数学学习策略现状的调查与分析[D]．上海：上海师范大学，2017：11–37．

[17] GLASS G V. Primary, secondary, and meta-analysis of research [J]. Educational Researcher, 1976, 5 (10): 3–8.

[18] HARRISON L L. Pulling it all together: The importance of integrative research reviews and meta-analyses in nursing [J]. Journal of Advanced Nursing, 1996, 24 (2): 224–225.

[19] 任志洪，赵春晓，田凡，等．中国人心理健康素养干预效果的元分析[J]．心理学报，2020，52（4）：497–521．

[20] CHENG H, WU G, GAO L, et al. Research on status and characteristics of the mastery of students’ mathematical learning strategies in Chinese junior high schools [J]. Procedia-Social and Behavioral Sciences, 2014 (116): 3 218–3 225.

[21] 付梦娟．中学生思维风格、数学学习策略与学业成绩的关系研究[D]．曲阜：曲阜师范大学，2012：7–18．

[22] 李冰．基于初中生数学学习风格的数学学习策略对数学学业成绩的影响[D]．长春：东北师范大学，2015：14–20．

[23] 刘丹．高效率数学学习初中生的数学学习策略特征研究[D]．天津：天津师范大学，2017：17–35．

[24] 沈利玲，孙霞．蒙汉族初中生数学学习策略调查研究[J]．吉林省教育学院学报（学科版），2010，26（2）：43–44．

[25] 王光明，李健，侯晓娟．初中生数学学习策略常模的建立及其应用案例——以天津市为例[J]．数学通报，2020，59（2）：4–9．

[26] 吴现荣，姚惠，宋军．贵州南部地区布依族初中生数学学习策略个体差异调查研究[J]．遵义师范学院学报，2016，18（5）：141–145．

[27] 张美玲．初中生数学学习策略及其与策略意识、思维风格、数学学业成绩关系[D]．温州：温州大学，2012：17–25．

[28] 白雪．高一学生数学学习策略的调查研究——以阜新市H和S高中为例[D]．沈阳：沈阳师范大学，2017：17–24．

[29] 包文真．高中生认知风格、数学学习策略、数学成绩关系的调查研究[D]．武汉：华中师范大学，2016：12–20．

[30] 蔡静雯．广西高二学生的数学学习策略差异调查研究——以桂林市某重点中学为例[D]．桂林：广西师范大学，2018：10–21．

[31] 李健，孙玥，王光明．高中生数学学习策略的常模及其水平等级标准研究——以天津市为例[J]．数学教育学报，2017，26（4）：8–14．

[32] 李雪．高中生数学认识信念与学习策略的关系及其对学业成绩的影响[D]．南京：南京师范大学，2018：14–43．

[33] 邵颖．高一学生数学学习策略应用现状及教育建议[J]．教育测量与评价（理论版），2015（6）：46–51．

[34] 宋健栋．高一学生数学学习策略调查研究[D]．烟台：鲁东大学，2017：10–19．

[35] 孙建萍．藏族高中生认知风格对数学学业成就的影响——数学元认知能力与学习策略的链式中介作用[D]．石家庄：河北师范大学，2020：16–29．

[36] 王煜，魏子亮．高中生数学逆商与数学学习策略的关系[J]．青海师范大学学报（自然科学版），2020，36（2）：68–76．

[37] 张爽．高一学生数学学习兴趣、成就目标定向、学习策略与学业成绩的关系研究[D]．长春：东北师范大学，2006：10–14．

[38] 张书朋，张庆垚，李彩娜．领悟社会支持性别差异的元分析[J]．心理发展与教育，2015，31（4）：393–401．

[39] 邱毅，郑晶玮．对我国发展中国家地位的思考与建议[J]．国际贸易，2020，57（1）：44–49．

[40] 哈里斯•库珀．元分析研究方法[M]．5版．北京：中国人民大学出版社，2020：148．

[41] 中华人民共和国教育部．关于印发《基础教育课程改革纲要（试行）》的通知[EB/OL].（2001–06–01）[2020–07–05]. http://www.gov.cn/gongbao/content/2002/content_61386.htm.

[42] XU B. Research on mathematics education in China in the last decade: A review of journal articles [J]. Frontiers of Education in China, 2010, 5 (1): 130–155.

[43] 刘电芝．高效学习的追求：学习策略的研究与实践[J]．中国教育科学，2019，2（6）：81–99．

[44] 刘电芝，朱江容，丁小强，等．策略意识对初中生数学学习策略的影响：策略情感的中介效应[J]．苏州大学学报（教育科学版），2015，3（1）：105–114．

[45] 刘电芝．中小学生学科学习策略的诊断与培育[M]．北京：人民教育出版社，2020：221．

[46] 张林，张向葵．中学生学习策略运用，学习效能感，学习坚持性与学业成就关系的研究[J]．心理科学，2003，26（4）：603–607．

[47] 马郑豫，张家军．中小学学生学习策略的调查研究[J]．教育研究，2015，36（6）：85–95．

[48] 庞祯敬，李慧．区域间普通高中教育均衡发展的思考与评价[J]．现代中小学教育，2014，30（8）：27–30．

[49] DONKER A S, D E BOER H, KOSTONS D, et al. Effectiveness of learning strategy instruction on academic performance: A meta-analysis [J]. Educational Research Review, 2014 (11): 1–26.

[50] PINTRICH P R, GROOT E V D. Motivated and self-regulated learning components of classroom academic perfor- mance [J]. Journal of Educational Psychology, 1990, 82 (1): 33–40.

The Application of Chinese Middle School Students’ Mathematics Learning Strategies: A Meta-Analysis

HE Mu-ye1, KOU Dong-quan2, LIU Dian-zhi1, JIANG Mao-xin1

(1. School of Education, Soochow University, Jiangsu Suzhou 215123, China;2. School of Educational Science, Yangzhou University, Jiangsu Yangzhou 225002, China)

Meta-analysis refers to the statistical analysis of a large number of analytical results from various studies with the aim of integrating the findings. This study uses meta-analysis techniques to investigate the application of Chinese middle school students’ mathematics learning strategies and their relationship with math achievement. The results showed thatage has no significant moderating effect on mathematics learning strategies.The application of mathematics learning strategies of middle school students showed a slight downward trend with the increase of grades. The moderating effect of region and gender on mathematics learning strategies emerges to the high school stage, and the mathematical cognitive strategies of high school students in underdeveloped areas are significantly lower than those in developed areas. Mathematical cognitive strategies have the highest correlation with mathematics achievement. This papersuggests that the development trend of mathematics learning strategies for middle school students is not optimistic. It is necessary to attach importance to the teaching of mathematics learning strategies in high school and consider mathematics cognitive strategies as the teaching focus.

middle school students; mathematics learning; learning strategies; meta-analysis

2021–10–03

教育部人文社会科学研究规划项目——认知负荷与情绪调节对学习策略使用的影响机制：以估算策略学习为例（18YJA190008）

何木叶（1982—），女，白族，云南大理人，副教授，博士生，主要从事学习心理研究．刘电芝为本文通讯作者．

G420

A

1004–9894（2022）02–0090–07

何木叶，寇冬泉，刘电芝，等．中国中学生数学学习策略运用的元分析[J]．数学教育学报，2022，31（2）：90-96．

[责任编校：陈汉君、张楠]