表征在数学教育中的研究现状

沈 阳，张晋宇，鲍建生

表征在数学教育中的研究现状

沈 阳1，张晋宇2，鲍建生1

（1．华东师范大学 数学科学学院，上海 200241；2．闵行区教育学院，上海 200241）

表征概念源于认知心理学，是影响数学学习的重要因素．采用混合研究法，基于中外两个重要的数据库ERIC和CNKI中与数学表征相关的249篇文章，从时间分布、研究对象、数学内容、研究主题及分析框架5个方面进行统计分析．研究结果如下：与数学表征相关的文献数量在最近10年增长速度显著；研究对象主要以学生为主，但教师和教材相关研究已成为趋势；数学内容多局限在代数方面，尤其方程与函数；在研究主题上，探究学生和教师的数学表征能力占主导；不同研究主题通常有不同的分析框架，用于分析各种数学表征方式、表征功能及表征转换．整体而言，从数学学习心理、数学问题解决及信息技术的角度对数学教学中的多元表征及其转换进行实证研究成为表征研究的一个基本趋势．

表征；数学教育；ERIC；CNKI

1 研究背景

表征（representation）一词源于认知心理学，1966年布鲁纳（Bruner）为描述儿童的思维活动将其引入数学教育领域，提出概念学习的活动性、图象性及符号性3种表征形式[1]，引起了数学教育界的广泛关注，尤其在数学学习心理和数学问题解决领域．莱什（Lesh）等认为学生理解数学的一个要素是能够表征数学，并在布鲁纳的基础上丰富了它的内涵，将线性方式发展的3类思维表征扩展为网状式的5类数学表征[2]，包括实际情境、操作模型、图表、口语和书写符号，而且强调了两两表征之间的相互转换．韬尔（Tall）在布鲁纳的基础上提出了3个世界理论[3]，包含具体化、符号化及形式化的世界，对应学生的思维发展过程．Brachman认为推理是对已知命题表征进行复制、移动、拆分等操作之后形成新的命题表征的过程[4]，所以表征总与逻辑推理息息相关．

除数学学习心理方面的研究，新世纪以来，数学表征已逐渐进入数学课程、评价等领域．例如，全美数学教师理事会（National Council of Teachers of Mathematics，简称NCTM）在2000年出版的《数学原则与标准》（）中，从过程和结果两个层面赋予“表征”意义，认为表征既指表达数学概念的行为，也指数学概念形式本身，既表示外部可观察到的，也表示内部不能观察到的过程与结果；数学表征也被认为是一种数学能力，内涵是指能够创造、选择或应用各种数学表征来解决数学问题[5]．2000—2021年的历届PISA测试，均把数学表征作为重要的数学素养评价指标；德国数学教育课程标准[6]、丹麦的KOM项目[7]等也都将数学表征列为数学教育目标．

相比于国外，国内在数学表征方面的研究起步较晚．不过早期也不乏从心理学模式研究问题表征，比如傅小兰等通过一道数学问题测试34名大学生对问题的信息加工过程，发现信息遗漏、信息误解以及隐喻干扰几类表征错误[8]；陈英和、仲宁宁等运用实验法、临床访谈法考察不同水平学生在解决应用题时表征策略的差异[9-11]；路海东等通过实验研究小学生解决和差问题的表征策略[12]；喻平等强调知识表征和数学学习之间的关系[13]，比较不同年级学生问题表征的差异性[14]，也探究问题表征与个体认知结构的相关性；纪桂萍等分析学生问题表征与心理表征之间的关系[15]．后期研究已不限于心理学，比如徐斌艳等从教学角度出发考察学生的表征和转换能力[16]，认为表征是作为问题解决的重要策略，包括形式化、图象、动作及语言化策略；其团队也从功能角度分析课程标准在历史进程中关于表达交流、操作转换以及建模应用3类不同表征的变化[17]．再比如陈志辉等基于数学核心素养的视角调查学生数学表征与转译能力[18]．

基于数学表征在数学教育中的重要性，许多研究团体和国际会议都设置了相关研究专题．例如，数学教育心理学国际研讨组（International Group for the Psychology of Mathematical Education，简称PME）在1989年专门成立数学学习过程中表征的研究工作组（http://www.igpme.org）；近几届的国际数学教育大会（International Congress on Mathematical Education，简称ICME）也将表征列入相关的课题研究组．比如，2021年在中国举办的第14届国际数学教育大会（ICME-14）中，有3个专题研究小组——数学教育中的符号学，数学教与学中的可视化、数学教育中的语言和交流（https://www.icme14.org/static/en/index.html），即对应数学表征的符号、可视化和语言3种表征形式．这说明，数学表征的相关研究已被国际数学教育界普遍关注．

中国新一轮课程改革的焦点是用数学核心素养统领课程、教学与评价，而数学核心素养中对“数学抽象”“直观想象”“数学建模”等的描述均与数学表征密切相关，因此，表征的研究对落实数学核心素养有重要的理论与实际意义．通过梳理近半个世纪关于数学表征的研究脉络，从时间分布、研究对象、数学内容、研究主题、分析框架5个方面分析表征在数学教育领域的研究现状，旨在揭示数学表征研究等基本问题与发展趋势．

2 研究过程

混合研究法（mixed methods）是同时或相继地运用定量和定性的方法来搜集和分析数据并用以解决问题的研究方法[19]．通过文献数量统计获取定量数据，用内容分析法对其文本属性或特征做出特定推断而获得定性数据，窥探其内容本质，为其做更详细的解释[20]．

教育资源信息中心（Education Resources Information Center，简称ERIC）是被教育研究者和实践者使用最为广泛的搜索引擎，2009年有120万个文献引文，其收录时间年限为1966年至今．中国知网（China National Knowledge Infrastructure，简称CNKI）所包括的《中国学术期刊（网络版）》是世界上最大的连续动态更新的中国学术期刊全文数据库，收录1915年至今的期刊．故用此两个数据库搜索国内外数学教育方面文献较为全面．

在ERIC中检索关键词“mathematical representation”，并粗略阅读所有结果的题目及摘要，选取关于数学表征的期刊文章及报告、合集—会议等，下载具有全文可得性（full-text availability）的文献．这些文章来源的期刊包含如“”等数学教育领域中的SSCI期刊，而不能全文下载的文章大多源自“”等小众期刊，且所占比例并不大，因此搜索到的全文可下载文献已然能覆盖数学教育绝大多数的文章，具有一定的代表性．获取1973年至2020年12月之前的文献173篇，同理在CNKI上获取1994年至2020年12月之前的文献76篇．

数据采集过程如下：首先将下载的249篇文献粗略阅读并排列；再将所有文献二次阅读，记录发表时间、研究对象、研究问题等内容，并标记典型特征；再在数据统计之后，根据数据特征对相关文献精细阅读并作质性分析．

3 研究结果

3.1 时间分布

呈现两个数据库的信息并非为了比较，而是为了观察国内数学教育领域对数学表征研究的现状．如图1所示，整体上两个数据库文献的数量呈波动上升趋势．自从布鲁纳将“表征”引入到数学教育领域后，表征开始应用于数学概念理解．从1973年开始，数学教育领域的学者陆续开始关注学生的表征能力．在1987年Janvier发表表征的综述之后，发表文献数量略微上升，并且在教师、课堂等的研究中也开始引入表征术语，到2004年ERIC数据库中出现一个小高峰，时隔十载，2013年的发文量再次出现高峰，到2019年发文量达到最高．

图1 文献年份分布趋势

国内表征的研究始于认知心理学，20世纪90年代被引入数学教育领域，不过其含义皆是借鉴了心理学中的概念．最初对表征的研究是基于思辨性的、介绍性的理论研究或心理学上的实证研究，且主要关注学生的数学知识表征、数学问题表征等，后来才转向关于课堂或教师．发文量在2005年前后相对较高，主要由于当时大批心理学家开展了关于学生数学表征的实验研究．在2013年之后数据明显上升，说明越来越多的研究者关注数学表征在数学教育领域中的作用．而且近两年撰写数学表征文章的作者多数来自一线教师，他们从数学表征角度对课堂教学案例进行设计和反思，意味着表征的研究已逐步进入一线教师实践领域．

3.2 研究对象

与数学表征相关的研究对象归为学生、教师、课堂、教材及理论5类，为了解不同年份间学者关注研究对象的变化，于是统计不同研究对象的文章在不同年份的数量．因为时间跨度较大，则以3年为单位，具体见表1．易见近一半的研究将学生作为对象，其次是教师和理论，关于课堂和教材的研究最少，不过近10年以来表征在教师和教材领域的研究数量有明显递增的趋势．而国内对表征的研究主要聚焦于学生和理论，较少涉及教师．

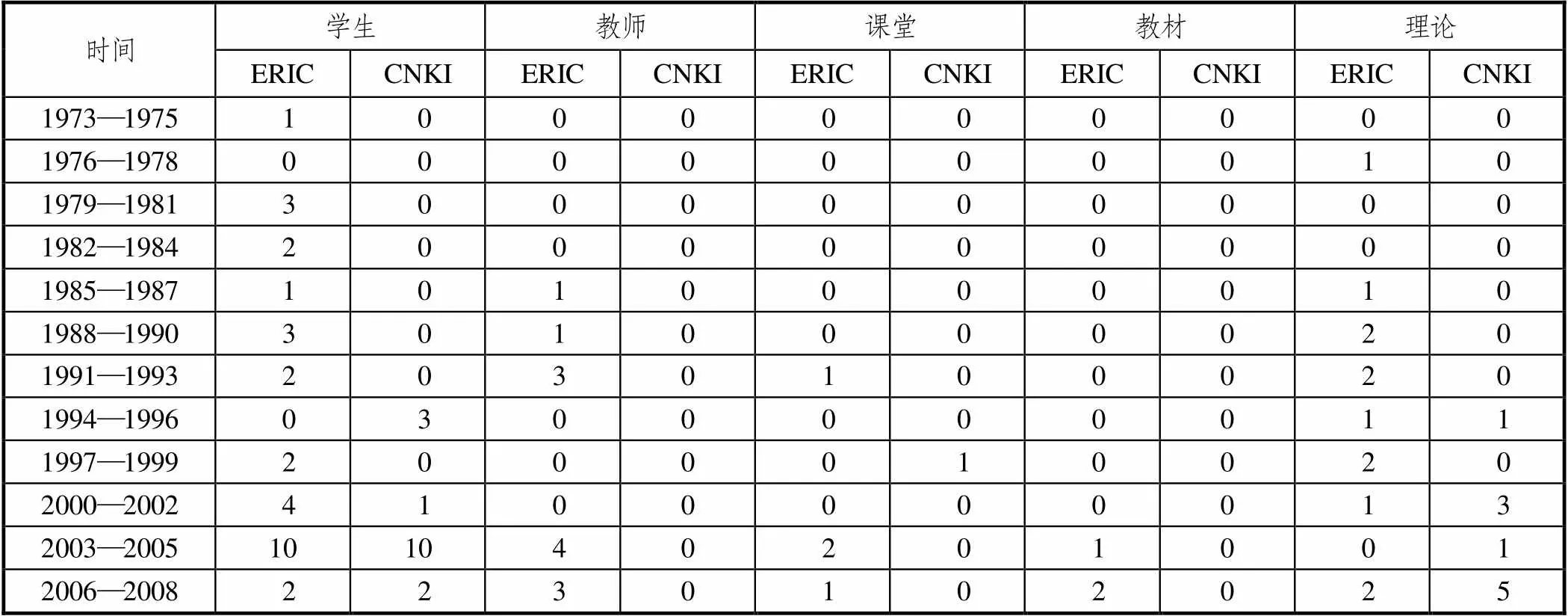
表1 不同时段文献数量分布

表1（续） 不同时段文献数量分布

关于数学表征研究最早是面向学生开始，金（King）于19世纪70年代通过测试了解不同年龄段学生的形象表征和符号表征能力，实则是为了证明布鲁纳的认知学习理论[1]．而且从表征角度研究学生一直以来并未间断，尤其在20世纪之后数量迅速递增．教师、课堂的表征研究均始于80年代前后，而20世纪之后才出现教材的表征研究，不过发文量基本都是逐年递增，尤其是教师和教材．国内最初的数学表征研究也是针对学生，比如大量研究从认知心理学角度探究学生的数学问题表征，一直以来学生作为对象的研究占据多数．同时国内不乏表征的理论辨析，其发文量也未呈现下降趋势．而课堂和教材的表征研究起步较晚，当一些技术软件应用于数学教学，教育工作者也开始考虑可视化表征对其教学的影响，因此近几年关于课堂的表征研究逐渐增多．

3.3 数学内容

由于数学各内容之间本身的交叉，故统计时并未过细区分，仅按照文献所提的数学内容归类统计，如图2所示，可见两个数据库的研究都主要以代数（数与运算、方程与函数、微积分）为主，几何次之，概率与统计最少．又因为数学内容与学段往往相关，因此也统计了文献的研究学段占比，如图3所示，可见表征的研究学段囊括幼儿、小学、初中、高中、大学5个阶段．对应其数学内容，研究者最为关注小学的数与运算以及初高中的方程与函数．

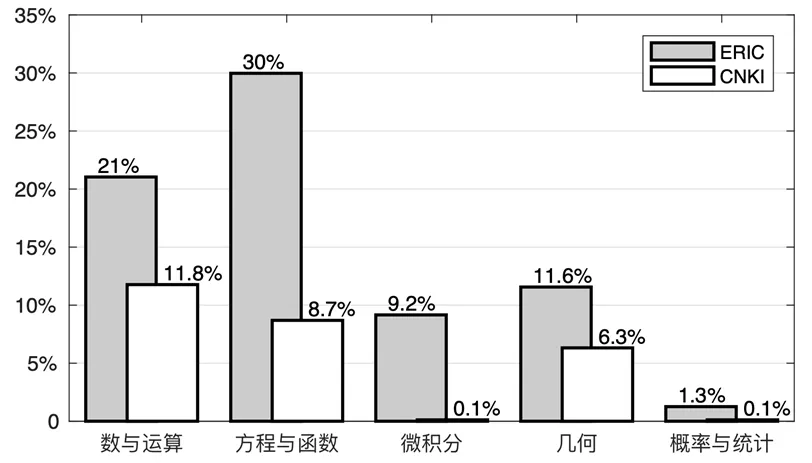
图2 文献研究内容占比

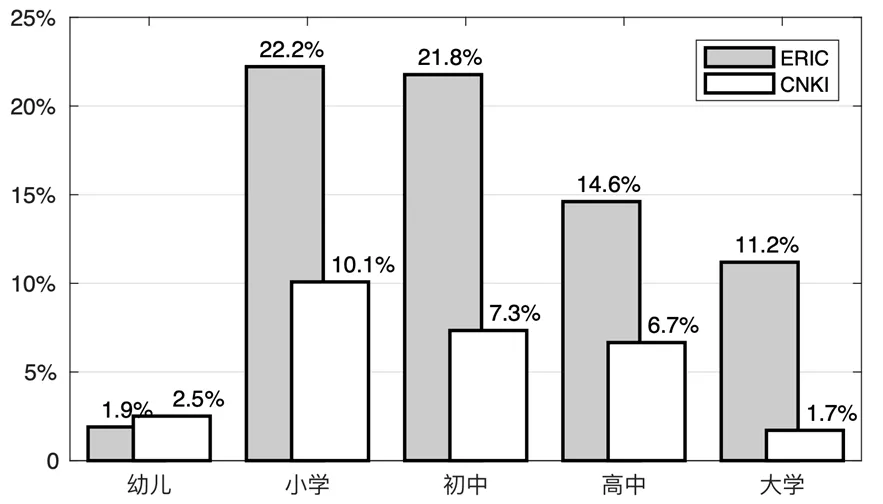
图3 文献研究学段占比

具体而言，幼儿阶段的表征研究主要关注数，比如通过数字的图象、符号等外在表征方式来帮助学生理解数的含义．小学阶段则涉及除微积分之外的所有数学内容，不过最为注重数与运算的表征，尤其分数的概念及运算．由于分数概念涵盖整体、测量、商、算子和比多重表征结构[21–22]，以及包括实物、表格等多种外在表征导致的复杂性使其通常成为小学数学教学的难点，自然成为研究者的关注对象．比如Andrade通过学生感受可触摸且可视化的分数表征，即制作钟表作为分数学习的脚手架，帮助学生理解分数[23]．初高中主要研究方程与函数的表征，尤其函数，德国数学家F·克莱因认为它是数学的“灵魂”．函数不同的表征转换、转换的内涵或者是计算机软件下图象的动态表征等均被研究者所关注．Janvier首先阐述了函数不同表征之间的转换功能，强调表征转换在数学理解中的作用[24]．之后研究者对其在实践方面进行多角度探讨，比如测试学生表征转换能力、学生在表征转换时出现的错误等．大学在表征上的研究主要延续函数内容，聚焦于研究微积分的多元表征、不同表征之间的联系与转换以及学生对其的表征过程．

3.4 研究主题

统计所有文献的研究问题，并据其对研究主题进行分类，归为表征能力、表征过程、表征使用、呈现表征及表征本身5类，见表2．表征是一个复杂的概念，在不同情境中有不同含义，所以作者会根据不同的需求选择不同的内涵．这里，表征能力（representation ability）是一种技能或素养[25]，指数学表征能力；表征过程（representation process）中的“表征”作为动词[26]，描述动态过程；表征使用（using representations）中的“表征”作为名词[27]，是以工具形式存在；表征特征（representation of）中的“表征”表示知识的呈现或表达[28]；表征本身（representation itself）是指表征概念或表征理论[29]．因为信息技术在各类研究中提及次数并不少，且对课堂教学呈现多元表征发挥巨大作用，所以也在此叙述．

（1）表征能力．

表征能力的研究对象主要为学生和教师，尤其是学生．这类研究通过调查、测量等方法了解学生和教师的数学表征能力现状或水平，占比最大（30.93%）．表征能力被PISA、NCTM等已赋予了丰富的内涵，而且PISA2000—2021年均将其作为学生数学基本能力之一．不过不同学者对表征能力研究的侧重仍不尽相同，比如Hwamg关注学生的多元表征能力，探究学生几何学习中多元表征能力是否影响学生的解题能力[36]；Hattkudur等聚焦学生建构表征的能力，测试学生在函数学习中建构图象表征的能力[37]；郭萌等注重学生的表征转换能力，调查五六年级学生的分数表征转换能力[38]．此类研究根据不同的研究目的而选择不同的数学内容，也通常与理解能力、问题解决能力等相联系，如杨红萍等研究学生问题表征能力与数学阅读能力间的关系[39]．由于教师本身的数学表征能力与将知识转化成让学生容易理解的知识的能力息息相关，因此也不乏对教师进行表征能力的测试，不过主要聚焦于职前教师，如Yilmaz等探究职前小学教师在问题提出中的多元表征能力[27]．

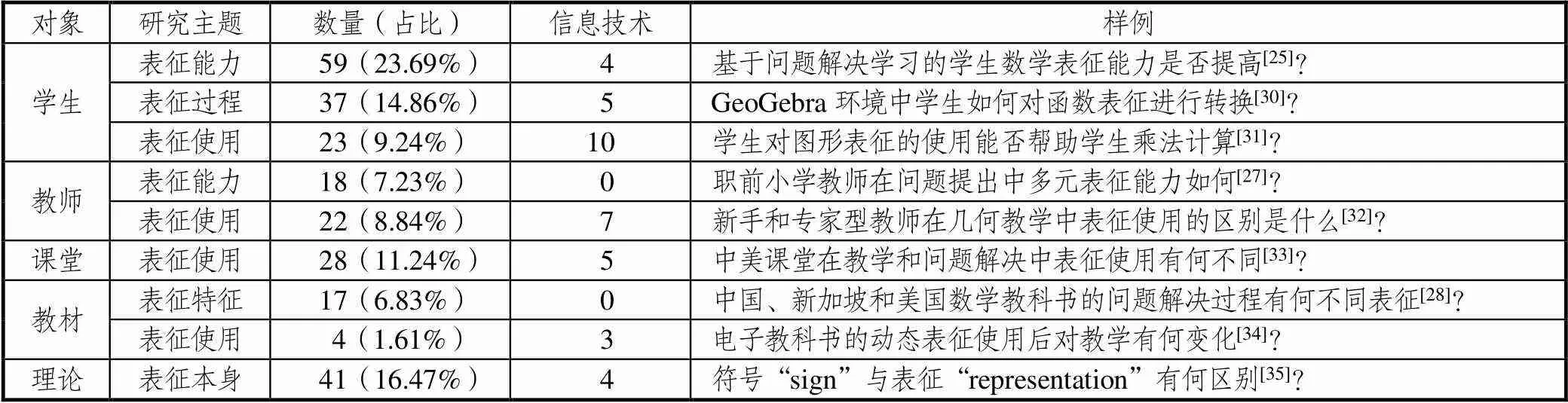
表2 不同研究主题文献数量分布

（2）表征过程．

表征过程的探究是为了呈现动态的行为特征，研究对象仅有学生．大多研究者通过测试或观察学生在某一领域数学问题的解答过程中发现学生表征过程的特点，例如，Adugymfi等通过测试学生在解答多项式函数来探究学生在代数与图象之间进行表征转换的特征[26]．这类研究的目的可以是为了分析学生的错误表征过程而间接帮助学生，亦或是探究动态表征是否更有助于学生理解，比如Daher等证明了GeoGebra通过呈现不同函数表征的转换确实帮助学生提高了解决数学问题能力[30]；也有不少学者探究学生的内部表征，即思维活动与外部表征之间的转换过程，比如Schindler等通过眼动跟踪方法探究建构整数表征的认知加工过程，目的旨在了解学生概念学习的内在认知过程[40]．

（3）表征使用．

表征使用中的“表征”作为一种工具，研究对象包括学生、教师、课堂以及教材，目的是为了帮助学生学习．关于学生表征使用的研究中一部分是探究使用不同表征能否帮助学生问题解决或概念学习，比如巴桑卓玛等探索藏族学生在问题解决中使用表征的特征[41]；大部分是探究信息技术支持下学生对动态表征的使用，如Ozgunkoca等比较技术软件呈现的不同表征对学生学习线性函数的效果[42]．教师表征使用研究的目的是为了在教学中帮助学生，比如Stylianou等比较新手与专家教师在几何教学中使用可视化表征的异同，结论是专家教师比新手教师使用可视化表征的频率更高，并且学生的理解更为深刻[32]；教师在表征使用中往往也会借助信息技术，例如Bleich等研究教师是如何通过动态软件使用图片表征来解决问题的，并且总结图片表征的功能包含交流、理解及美观3类[43]．课堂中表征使用的研究实际上指教学活动中学生或教师对表征的使用，如蔡金法等比较中美课堂发现亚洲课堂的师生习惯使用符号表征，而美国师生喜欢使用口头表征和图片表征[33]．教材对表征的使用体现在电子教材中，如Yerushalmy等探究在技术支持下电子教科书中使用动态表征后教学的变化[34]．

（4）表征特征．

在展现教材的特点时经常会用“表征”一词，大多是通过单本或者比较多本不同版本教材而呈现教科书的表征，这里表征的含义与呈现相同．不过呈现教材特点也会从诸多方面考虑：有对问题解决过程的描述，比如范良火等比较不同国家数学教科书中数学问题解决过程的不同表征[28]；有从概念编排角度的探究，比如章飞等从概念形成、概念同化、概念建构等方面展现教科书概念的表征方式[44]；有从语言学视角切入的研究，如Österholm比较语言的简洁度、复杂性、关系、人称来展现教科书的特征[45]；也有通过数学问题的多元表征或者转换来叙述，例如很多研究者通过分析数学问题的口语、符号、图象或混合表征来呈现特点，再比如Chang将微积分教科书的特征通过问题的代数符号、图象、表格、文本表征之间的转换来展现[46]．

（5）表征本身．

表征本身内涵丰富，在认知心理学中指人脑内部的心智活动，又可指思维活动的外在表现形式，可表示数学关系的过程，也表示关系的形式[6]，所以研究者会根据情境的不同而选取不同的内涵．对于表征本身的研究，有从表征词性分析，比如Iori分析教学过程中“sign”与“representation”的差异[35]；更多的是从内部表征、外部表征、多元表征、表征转换、表征能力、表征灵活性等多个子概念分析．从数学知识角度考虑，数学内部表征指不同数学结构之间的关联，外部数学表征指数学人工符号系统；从概念认知角度考虑，内部表征被认为是个人的心理表征，一般不能被直接观察到，而外部表征指可触摸的有形的行为或对象，并且外部和内部表征之间是互动的[47]．多元表征一般指多元外部表征，而且不少研究证明学生使用多元表征比单个表征更助于理解数学．表征转换表示不同表征之间的相互变换，于学生而言，这种转换能力即表征能力之一，表征灵活性也就成为其表征能力评价指标之一[48]．数学表征能力被NCTM中以过程标准提出，主要是指学生能够在问题解决和学习中具有创建、使用、选择、应用以及转换表征的能力[5]，与PISA中的定义差异不大．结合表1发现国内关于表征理论的介绍不在少数，主要以思辨方法综述表征的定义、应用或功能．

（6）信息技术．

Kaput于1986总结表征的两种功能，一是数学本身可以作为思维和交流的工具，二是信息技术的引进可以提供新的或多元的表征[29]．表2表明信息技术在各研究对象中均有参与，说明引入信息技术而提供新的表征、多元表征或者可视化表征已引起学者的关注，例如Santostrigo等探究如何用动态软件表征圆锥曲线促使问题更容易被理解[49]．对于学生而言，信息技术提供的表征是为了帮助自己理解数学概念；于教师而言，如何利用信息技术来帮助学生学习而让课堂变成高效课堂是其追求的目标；于教材而言，电子教科书除却迷你，便于携带的优点外，更具特色的是可以提供多元的、动态的表征．对于信息技术的引入，虽然诸多研究表明多元表征可以加深学生对数学概念的理解，但有时也会适得其反，比如Ainsworth等通过实验证明在技术支持下多元表征环境中，学生估算能力反而下降[50]．

3.5 分析框架

大部分研究者会参照NCTM中对数学表征能力的界定，实际上归纳为表征交流能力、表征转换能力以及表征建模能力．徐斌艳等区分数学表征能力以及表征转换能力，认为数学表征能力是用符号、图表、文字等某种形式，表达数学概念或关系从而解决问题；数学转换能力则解释为为了简化或解决问题而使用改变信息形态的数学转化策略[51]．并将表征能力划分为3个水平，水平一指能够针对数学对象提出并利用标准化表征，水平二为可以清晰地解释给出的数学表征并转换不同的表征形式，水平三为理解并应用不熟悉的表征，能够针对问题创建新的表征且有目的地评价表征[6]．

多数研究者会采用质性分析法描述表征过程，主要针对学生解题过程．Adugymfi等为描述学生数学表征转换过程而开发的模型可以清晰地描绘学生解题时表征转换的行为以及解题过程中所犯的错误类型[26]，如图4所示．由于表征转换指表征之间的变换，故有源表征和靶表征两个概念．源表征经历中间不同的过程后得到靶表征，并且循环过程可经历一次也可经历多次．其循环中的等值转换指从源表征到靶表征传递的信息是等价的，即在转换源表征的过程中保留了所有信息；性质转换指理解和识别源表征所具备的特征或性质，比如在转换函数图象为解析式的过程中，识别和理解图象上点、线含义的过程即为性质转换；操作转换指运算等操作过程，例如根据表格中的点绘制图象的过程．等值转换与性质转换两个过程具有相似性，均保持了语义的一致性．差别在于，性质转换过程的靶表征上仅呈现源表征中明确的信息，而等值转化过程的靶表征中会呈现源表征中不是很明确的信息．因此，在描述学生表征转换的过程中即能诊断出学生的错误原因，包括操作转换中出现的操作错误，或性质转换中的解释错误，亦或等值转换中的保留错误．

Ainsworth针对多元表征环境学习设计的DeFT（Design，Function，Tasks，简称DeFT）分析框架针对课堂、教师和学生[52]，包含设计、功能、任务3个维度．设计维度指教师为多元表征环境的课堂而从数量、信息、形式、序列、转换方面所作的设计．表征数量指表征的频次；信息分布指信息在不同表征上的分布；表征形式指照片、文字、动画等表征的方式；表征序列指产生表征的先后顺序；表征转换指表征之间的相互转换．表征的设计实际上隐含着教学功能，即框架的第二个维度，包括互补、解释和深度理解功能．互补功能指不同表征所携带的信息可以相互弥补；解释功能指利用多元表征更为有效地解释信息；深度理解指通过多元表征的迁移构建更深层次的理解．任务实际上是学生在课堂中所应具备的表征能力．首先，学生应该理解表征的形式，知道表征的编译过程以及表征所表示的信息，比如需要知道表格由行、列、标签等组成；其次，学生应理解表征与领域间的关系，比如在只有时间、距离两个变量的图表征上读取速度时，需要理解图表与速度之间的关系；第三、学生应该学会选取适当的表征，比如选择折线图来表示变化趋势；最后，学生应该学会构建新的表征，比如有研究表明学生在绘制图表，即创造新的表征时，比仅选择已有图表更有利于培养学生的逻辑推理．

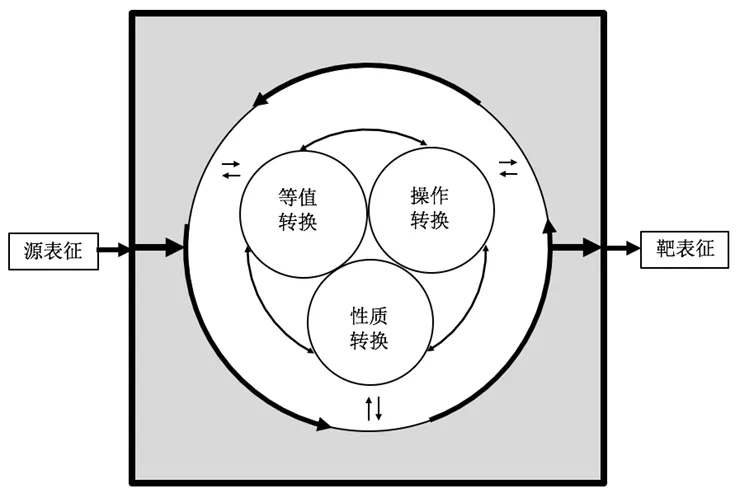
图4 学生表征转换过程模型

教材的表征研究更多的是呈现其表征特点，现较为常见的分析框架如表3所示[53]．对数学教材的活动、例题和练习题从表征、任务情境及认知需求水平进行分析．宏观角度即选取教科书的数学内容的分类．微观角度即具体分析的维度，表征是展示问题的表示形式，任务情境是问题设置的背景，认知需求即问题的难易程度．该框架除了可以获取教材外在的数学表征特点之外，还能获取教材难易程度或对学生认知要求的信息．

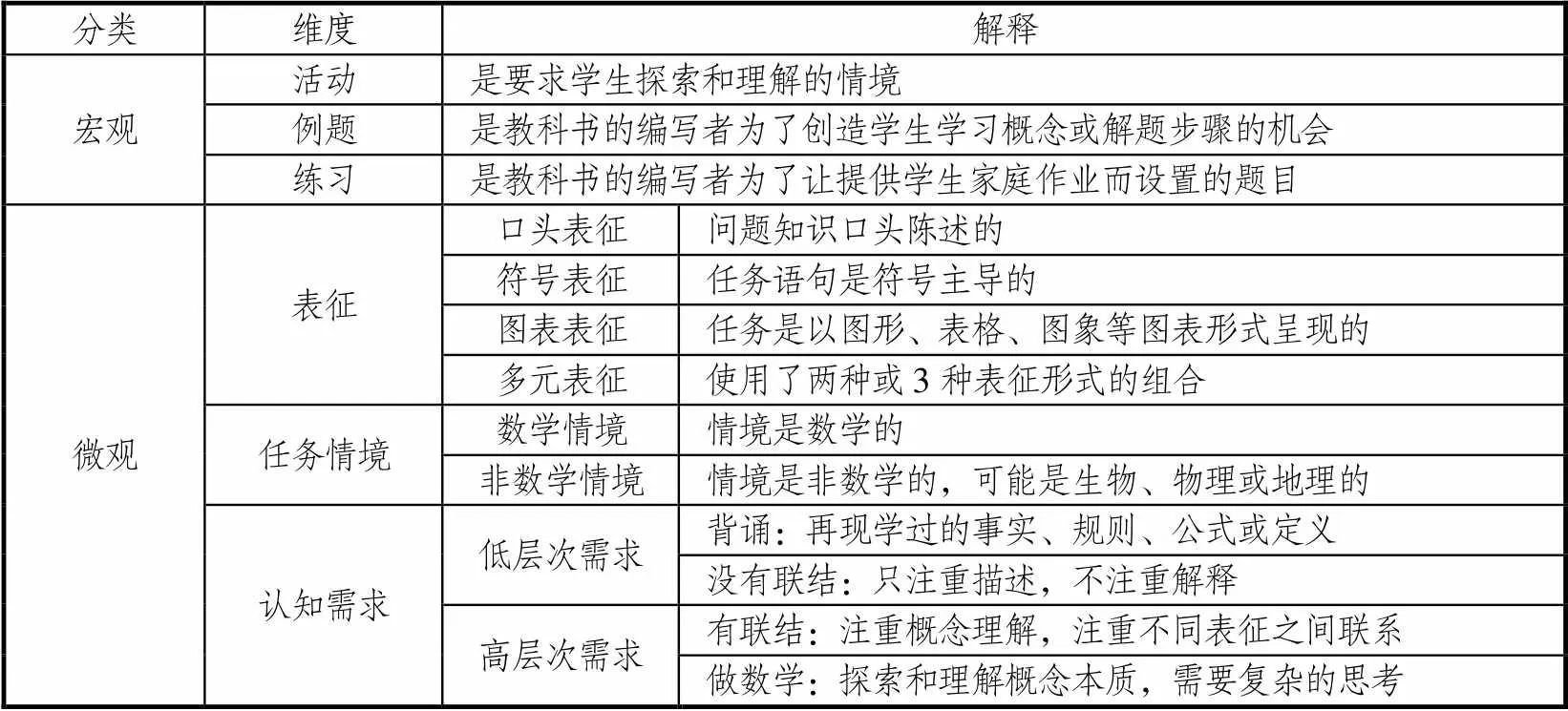
表3 教材中数学表征的分析框架

关于表征本身，韬尔最初是从布鲁纳的3种表征得到启发，在经历一系列的实践修改后总结出数学的“三个世界”理论，为具体化的、符号化的以及形式化的世界，对应布鲁纳的动作性、算术的符号以及逻辑的符号表征．图5所示的框架[3]是在原来“三个世界”的基础进行了调整，对应学生的思维发展过程．具体化概念保持不变，依旧表示具体的、物理的、形象的数学概念；符号化概念进行了窄化，定义为操作的符号化，仅聚焦于符号的运算与操作，并且将其统称为经验的数学．扩大了形式化概念内涵，定义为公理的形式化，并且从理论的数学及公理形式化的数学两个维度讨论：理论的数学是通过已知对象的性质、操作性质推理而成，比如欧氏几何学中所出现的定理；公理化形式化的数学是在集合论的基础上，通过形式化的逻辑推导或证明而得到的性质．数学思维长期的发展过程最初是先掌握具体化的概念表征，然后通过操作方式掌握操作性的符号化表征，这也就形成了经验的数学；之后通过感知的方式进行概念的推理，或者操作符号进行推理与证明，从而形成理论的数学，即形式化数学中的一部分；最后在具体化表征和符号化表征基础上发展为形式化表征．自然地，在数学思维达到公理的形式化阶段后，可以产生更多的具体化和符号化来促进数学学习．

图5 数学的“三个世界”理论

4 研究展望

4.1 数学学习心理

表征本身源于认知心理学，引入数学教育领域，一方面是解析学生数学学习的内部表征，从而了解学生的思维发展过程，另一方面教师可以根据认知规律更具针对性地作教学设计．虽然中国早期不乏从心理学角度探讨数学表征，但依旧未形成系统的实践理论．目前在数学核心素养统领的新课程改革中，越来越多的一线教师开始关注表征在课堂中的作用，试图使用学生更易接受的表征形式来降低学生学习的认知负荷．然而教师对表征的使用仅局限在外部表征层面，对教学的设计很少能够真正从学生的思维发展过程考虑．因此从一线教师视角切入表征的研究可以从以下方面进行：首先可以从表征角度深入探究培养数学核心素养的心理认知过程，为教师更好地落实数学核心素养提供理论依据；其次，完善表征在数学学习心理的实践理论，为教师诊断学生的数学思维、合理设计多元表征环境的教学设计提供思路．

4.2 数学问题解决

加涅认为问题解决是一种高级规则的学习，表征是解决数学问题的必备能力．首先，学生需要表征数学问题，包括字面的理解以及问题的深层理解，即学生头脑中对数学问题的重述，这一步骤在很大程度上是学生能否解题的关键．其次，解决数学问题的过程需要表征转换，而且需要避免出现概念理解或操作性的错误．所以学生对问题的表征能力以及不同表征之间转换的能力尤为重要．而大部分研究聚焦于学生问题表征能力的现状或水平，或者问题表征过程特征的呈现，对于如何通过问题解决培养学生表征能力的研究较为匮乏．基于此，从期望课程的角度考虑，教科书中的数学问题的表征方式、表征过程以及它需要培养学生的哪些素养是值得思考的问题．从实施课程的角度思考，中国对教师或者职前教师的表征研究原本甚少，所以教师本身如何在课堂中呈现数学问题的合理表征，如何对学生在问题解决过程中的表征错误进行对症下药，或者教师本身所具备多少表征能力等都值得深入研究．

4.3 信息技术使用

在前文不同对象的研究主题中，或多或少都有提到信息技术的使用．Kaput在20世纪80年代已关注到信息技术的引入导致数学教育的变化，不仅能够提供不同表征形式的转换，还可以直观呈现新的表征形式、多元表征、联结表征等．现阶段教师越来越重视动态的、联结的数学表征，使用几何画板、GeoGebra等软件教学已然成为数学教学的流行方式．尤其在后疫情时代，数学教育与信息技术不容分割．大部分研究表明课堂上由信息技术带来的表征形式有助于学生理解数学，但是反对的声音也逐渐增多．天花乱坠的动态、可视化、多元的表征形式所充斥的课堂，是否真的有助于学生学习；是否对于所有学生都起到正面作用．所以亟需相关的实证研究为信息技术在课堂中的使用提供教学策略，一方面需要思考如何在课堂中有效使用信息技术；另一方面需要考虑哪些数学内容的表征适合在课堂教学中引入动态软件．

[1] KING I. Ikonic and symbolic representation: A study of mathematical reasoning [J]. Cognitive Development, 1973, 14 (1): 1–13.

[2] LESH R, POST T, BEHR M. Representations and translations among representations in mathematics learning and problem solving [M] // JANIVER C. Problems of representations in the teaching and learning of mathematics. Hillsdale, NJ: Lawrence Erlbaum Associates, 1987: 33–40.

[3] TALL D. Making sense of mathematical thinking over the long term: The framework of three world of mathematics and new developments [M] // TALL D, WITZKE I. Mintus: Beiträgezur mathematischen, naturwissenschaftlichen und technischen Bildung. Wiesbaden: Springer, 2020: 1–26.

[4] BRACHMAN R, LEVESQUE H J. Knowledge representation and reasoning [M]. San Francisco: Morgan Kaufmann Publishers, 2004: 4.

[5] NCTM. Principles and standards for school mathematics [M]. NCTM, 2000: 67.

[6] 徐斌艳．关于德国数学教育标准中的数学能力模型[J]．课程·教材·教法，2007，27（9）：84–87．

[7] NISS M. Mathematical competencies and the learning of mathematics: The Danish KOM project [C] // GAGATSIS, ATHANASIOS. 3rd mediterranean conference on mathematical education: Mathematics in the modern world, mathematics and didactics, mathematics and life, mathematics and society. Athens: Hellenic Mathematical Society; Cyprus: Cyprus Mathematical Society, 2003: 115–124.

[8] 傅小兰，河海东．问题表征过程的一项研究[J]．心理学报，1995，27（1）：204–210．

[9] 陈英和，仲宁宁，田国胜，等．小学二～四年级儿童数学应用题表征策略差异的研究[J]．心理发展与教育，2004，20（4）：19–24．

[10] 陈英和，仲宁宁，赵宏，等．小学二～四年级儿童数学应用题表征策略对其解决不规则问题影响的研究[J]．心理科学，2005，28（6）：1 314–1 317．

[11] 仲宁宁，陈英和，王明怡，等．小学二年级学生学优生与学困生应用题表征策略差异比较[J]．中国特殊教育，2006，69（3）：63–68．

[12] 路海东，董妍．小学生表征数学应用题策略的实验研究[J]．心理发展与教育，2003，19（1）：60–63．

[13] 喻平．知识表征与数学学习[J]．上海师范大学学报（哲学社会科学·教育版），2002，31（9）：49–52．

[14] 喻平．不同年级中学生对数学问题表征的差异性研究[J]．应用心理学，2005，11（2）：110–115．

[15] 纪桂萍，焦书兰，何海东．小学生数学问题解决与心理表征[J]．心理发展与教育，1996，12（1）：29–32．

[16] 徐斌艳．数学学科核心能力研究[J]．全球教育展望，2013，42（6）：67–74，95．

[17] 沈阳，张晋宇，李娜，等．20世纪以来中国数学课程标准中算数与代数表征功能的变化及启示[J]．数学教育学报，2019，28（3）：12–17．

[18] 陈志辉，孙虎，周芳芳．上海七年级学生“平行”概念表征与转译的调查研究——基于数学核心素养的视角[J]．数学教育学报，2019，28（1）：37–42．

[19] HART L C, SMITH S Z, SWARS S L, et al. An examination of research methods in mathematics education [J]. Journal of Mixed Methods Research, 2009 (3): 26–41.

[20] BIKNER-AHSBAHS A, KNIPPING C, PRESMEG N. Approaches to qualitative research in mathematics education [M]. Dordrecht: Springer, 2015: 365.

[21] CHARALAMBOUS C Y, PITTA-PANTAZI D. Drawing on a theoretical model to study students’ understandings of fractions [J]. Educational Studies in Mathematics, 2007 (64): 293–316.

[22] 赵莉，王春英，史宁中．分数概念表述和分数除法运算的比较研究及其对教学的启示[J]．数学教育学报，2021，30（3）：46–51．

[23] ANDRADE A. The clock project: Gears as visual-tangible representations for mathematical concepts [J]. International Journal of Technology & Design Education, 2011 (21): 93–110.

[24] JANVIER C. Translation process in mathematics education [M] // JANIVER C. Problems of representations in the teaching and learning of mathematics. Hillsdale, NJ: Lawrence Erlbaum, 1987: 27–32.

[25] MINARNI A, NAPITUPULU E E. Developing instruction materials based on joyful PBL to improve students mathematical representation ability [J]. International Education Studies, 2017 (10): 23.

[26] ADU-GYMFI K, CHANDLER K. Student connections between algebraic and graphical polynomial representations in the context of a polynomial relation [J]. International Journal of Science and Mathematics Education, 2017 (15): 915–938.

[27] YILMAZ Y, DURMUS S, YAMAN H. An investigation of pattern problems posed by middle school mathematics preservice teachers using mutiple representation [J]. Journal of Research in Education and Science, 2018, 4 (1): 148–164.

[28] FAN L, ZHU Y. Representation of problem-solving procedures: A comparative look at China, Singapore, and US mathematics textbooks [J]. Educational Studies in Mathematics, 2007 (66): 61–75.

[29] KAPUT J J. Information technology and mathematics: Opening new representational windows [J]. Journal of Mathematical Behavior, 1986 (5): 28.

[30] DAHER W M, ANABOUSY A. Students’ recognition of function transformations’ themes associated with the algebraic representation [J]. Journal of Research in Mathematics Education, 2015 (4): 179–194.

[31] BARMBY P, HARRIES T, HIGGINS S, et al. The array representation and primary children’s understanding and reasoning in multiplication [J]. Educational Studies in Mathematics 2009 (70): 217–241.

[32] STYLIANOU D A, SILVER E A. The role of visual representations in advanced mathematical problem solving: An examination of expert-novice similarities and differences [J]. Mathematical Thinking & Learning, 2004 (6): 353–387.

[33] CAI J, JR F K L. Solution representations and pedagogical representations in Chinese and U.S. classrooms [J]. Journal of Mathematical Behavior, 2005 (24): 221–237.

[34] YERUSHALMY M. Functions of interactive visual representations in interactive mathematical textbooks [J]. International Journal of Computers for Mathematical Learning, 2005 (10): 217–249.

[35] IORI M. Objects, signs, and representations in the semio-cognitive analysis of the processes involved in teaching and learning mathematics: a duvalian perspective [J]. Educational Studies in Mathematics, 2017 (94): 275–291.

[36] HWANG W Y, CHEN N S, DUNG J J, et al. Multiple representation skills and creativity effects on mathematical problem solving using a multimedia whiteboard system [J]. Journal of Educational Technology & Society, 2007 (10): 191–212.

[37] HATTIKUDUR S, PRATHER R W, ASQUITH P, et al. Constructing graphical representations: Middle schools’ intuitions and developing knowledge about slope and Y-intercept [J]. School Science & Mathematics, 2012 (112): 230–240.

[38] 郭萌，熊妍茜，杨新荣，等．五年级和六年级学生分数表征转化能力的调查研究[J]．数学教育学报，2016，25（5）：49–54．

[39] 杨红萍，肖志娟．问题表征对数学阅读能力的影响研究[J]．数学教育学报，2019，28（2）：70–74．

[40] SCHINDLER M, BADER E, LILIENTHAL A J, et al. Quantity recognition in structured whole number representations of students with mathematical difficulties: An eye-tracking study [J]. Learning Disabilities: A Contemporary Journal, 2019, 17 (1): 5–28.

[41] 巴桑卓玛，史宁中，覃若男，等．藏族小学数困生应用题表征特点研究——以藏族四年级学生为例[J]．数学教育学报，2021，30（1）：97–102．

[42] OZGUNKOCA A S A. The effects of multiple linked representations on students’ learning of linear relationships [J]. Hacettepe University Journal of Education, 2004 (26): 82–90.

[43] BLEICH L, LEDFORD S, HAWLEY C, et al. An analysis of the use of graphical representation in participants’ solutions [J]. Mathematics Educator, 2006 (16): 22–34.

[44] 章飞，俞梦飞，顾继玲．初中数学教科书中概念的呈现方式及一致性研究[J]．数学教育学报，2021，30（5）：21–27．

[45] ÖSTERHOLM M. What is so special about mathematical texts? Analyses of common claims in research literature and of properties of textbooks [J]. ZDM, 2013 (45): 751–763.

[46] CHANG B L, CROMLEY J G, TRAN N. Coordinating multiple representations in a reform calculus textbook [J]. International Journal of Science and Mathematics Education, 2016 (14): 1 475–1 497.

[47] GOLDIN G A, KAPUT J M. A joint perspective on the idea of representation in learning and doing mathematics [C] // STEFFE L P, NESHER P, COBB P, et al. Theories of mathematical learning. Mahwah, NJ: Erlbaum, 1996: 397–430.

[48] NISTAL A A, DOOREN W V, CLAREBOUT G, et al. Conceptualising, investigating and stimulating representational flexibility in mathematical problem solving and learning: A critical review [J]. ZDM, 2009 (41): 627–636.

[49] SANTOS-TRIGO M, ESPINOSA-PEREZ H, REYES-RODRIGUEZ A. Connecting dynamic representations of simple mathematical objects with the construction and exploration of conic sections [J]. International Journal of Mathematical Education in Science & Technology, 2008 (39): 657–669.

[50] AINSWORTH S, BIBBY P, WOOD D. Examining the effects of different multiple representational systems in learning primary mathematics [J]. Journal of the Learning Sciences, 2002 (11): 25–61.

[51] 徐斌艳．数学学科核心能力研究[J]．全球教育展望，2013，42（6）：67–74，95．

[52] AINSWORTH S. DeFT: A conceptual framework for considering learning with multiple representations [J]. Learning & Instruction, 2006 (16): 183–198.

[53] BAYAZIT I. Quality of the tasks in the new Turkish elementary mathematics textbooks: The case of proportional reasoning [J]. International Journal of Science & Mathematics Education, 2013 (11): 651–682.

Research Status of Representation on Mathematics Education

SHEN Yang1, ZHANG Jin-yu2, BAO Jian-sheng1

(1. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;2. Minhang Institute of Education, Shanghai 200241, China)

The concept of representation originates from cognitive psychology and is an important factor affecting mathematics learning. Using a mixed methods approach, the present study is aiming to analyze the studies on representation in the field of mathematics education, based on 239 papers related to mathematical representation in two important domestic and foreign databases, ERIC and CNKI. These papers are statistically analyzed from five aspects, i.e., the time distribution, research objects, mathematical content, research topics and analysis framework. Main results are as follows: the number of literatures related to mathematical representation has increased significantly in the past 10 years; in term of the research objects, most studies were focused on students, but the studies related to teachers and textbooks have become a trend; the content of mathematics is mostly limited to algebra, especially equations and functions.In terms of the research topic,the exploration of the mathematical representation ability of students and teachers dominates. From the perspective of analytical framework, different research topics usually have different analytical frameworks for analyzing various modes of representation, the function of representation and representation transformation in mathematics. On the whole, it has become a basic trend of representation research to carry out empirical research on multiple representations and their transformations in mathematics teaching from the perspectives of mathematical learning psychology, mathematical problem solving and information technology.

representation; mathematics education; ERIC; CNKI

2021–11–20

教育部人文社会科学重点研究基地重大项目——义务教育阶段数学学科核心能力模型与测评框架研究（11JJD880027）；上海市核心数学与实践重点实验室基金（18dz2271000）

沈阳（1992—），女，浙江东阳人，博士生，主要从事数学课程与教学论研究．

G420

A

1004–9894（2022）02–0082–08

沈阳，张晋宇，鲍建生．表征在数学教育中的研究现状[J]．数学教育学报，2022，31（2）：82-89．

[责任编校：周学智、陈汉君]