中美高考数学试卷比较研究

韩金璇，杨泽恒，王彭德

中美高考数学试卷比较研究

韩金璇1，2，杨泽恒1，王彭德1

（1．大理大学 数学与计算机学院，云南 大理 671003；2．南开中营小学，天津 300110）

SAT是美国应用广泛的大学入学考试，与中国高考类似，对高中教育有一定引领，分析比较两者数学试题，对中国高中及大学数学教育改革有一定意义．基于全国高考大纲、综合难度模型、数学核心素养、PISA测试情境，对SAT Ⅰ、SAT Ⅱ、中国高考数学试题进行比较，研究发现：SAT Ⅰ与SAT Ⅱ代数占比最高，中国几何占比最高；SAT Ⅰ超六成考查初中知识，SAT Ⅱ部分知识超出中国高考大纲．综合难度、推理能力等因素中国最难，SAT Ⅰ最易，SAT Ⅱ居中；SAT Ⅰ背景因素难度最大；中国与SAT Ⅰ含参数难度相近，均高于SAT Ⅱ．数学核心素养考查分布3卷总体一致，直观想象权重中国最高．SAT Ⅰ包含PISA的4类情境，中国与SAT Ⅱ未覆盖PISA所有情境类型．在因材施教、激发学生内生动力等方面获得启示．

综合难度模型；SAT数学；高考数学；比较研究

1 问题提出

大学入学考试是高中毕业生获得大学入学资格的重要测试，对中学教育有重要的引领作用，对高等教育有重要意义．近年来，国际大学入学数学考试对比研究以试卷难度对比为研究热点．谢晓川、方浩颖等[1]通过“背景、数学认知、运算、推理、知识含量”5个因素对中国2018年理科数学试卷和英国2018年A-level数学试卷的难度进行比较．武小鹏、张怡[2]在以上5个因素的基础上，增加了“思维方向、是否含参”两个因素，对中韩两国近3年高考数学试题进行比较．李保臻、石烨[3]进一步增加“梯度”因素，比较研究了中国大陆与台湾地区高考数学试题难度．张玉环、周侠[4]利用文[2]中难度模型对中法高考数学试卷进行比较．这些比较研究都基于鲍建生提出的综合难度模型理论[5]，从因素、权重系数等方面改进了模型．

SAT（Scholastic Assessment Test）是美国应用广泛的大学入学考试，与中国高考均为面向高中毕业生的选拔性考试．SAT数学分为SAT Ⅰ数学及SAT Ⅱ数学，SAT Ⅰ数学重视在真实情境中解决问题，关注学生与现实世界的联系．SAT Ⅱ数学内容更广泛深入，涉及大学数学知识，更重视数学综合能力考查．由于SAT Ⅰ数学更具基础性，考生面更广，现有研究主要针对SAT Ⅰ数学，常将SAT Ⅰ简称为SAT进行比较研究．

石凤雪[6]等对SAT的组织形式、招生模式及数学命题目进行对比．马玮[7]、黎郭凯[8]、王奋平[9]、刘思庄[10]选择SAT及中国高考数学不同试卷进行了比较．已有研究定性描述较多，整体定量分析少，缺乏对整套试卷全面定量分析．SAT Ⅱ与中国高考数学试题的比较也很少．从内容、难度、数学核心素养和PISA问题情境4个视角，同时将SAT Ⅰ、SAT Ⅱ与中国高考数学卷进行整体比较的研究还未见．从这4个视角定量对SAT Ⅰ、SAT Ⅱ与中国高考数学卷进行整体比较研究，对中国高考改革及高中教学有一定借鉴意义．

2 研究对象

选取2018年中国高考理科数学全国卷Ⅲ（以下简称卷1）、2019年4月SAT Ⅰ数学卷（以下简称卷2）、2019年5月SAT Ⅱ数学卷（以下简称卷3）进行比较分析．

3 研究过程及讨论

3.1 试题内容

将中国《2019普通高等学校招生全国统一考试大纲（理科数学）》[11]知识范围视为高中范围．由于SAT Ⅰ及SAT Ⅱ涉及初中知识和超出大纲知识，故将知识范围划分为初中、高中及超纲．将知识内容划分为3个领域：代数、几何、概率与统计．

对于考查初中知识的题，以《义务教育数学课程标准（2011年版）》[12]为主要依据标注知识点．SAT常考比例，在初中范围增加了比例．对于考查高中知识题目，以大纲为依据标注知识点．对于超纲知识，分为数与式、函数、级数、行列式4类．例1、例2分别是较为典型初中及超纲试题．

例1 若7(2-5)-2(2-5)=4(+5)，则的值为？（2019年美国SAT Ⅰ数学试题第6题）

例2 无穷级数的通项可表示为

将3份试卷所有试题考查知识点进行标定，整理和统计，得到3份试卷知识点分布情况（见表1～3、图1～2）．

表1 初中范围知识点分布情况

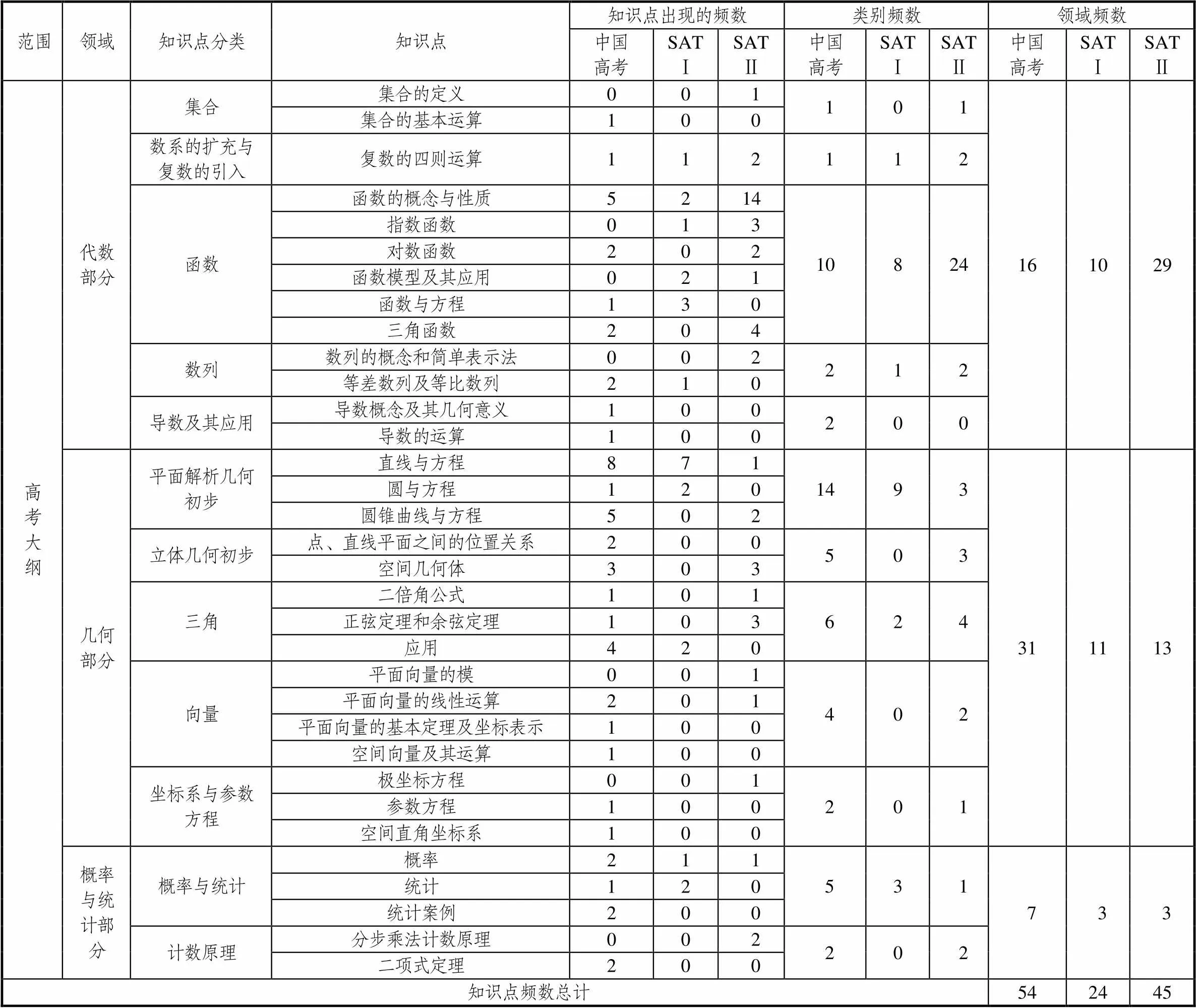
表2 高中范围知识点分布情况

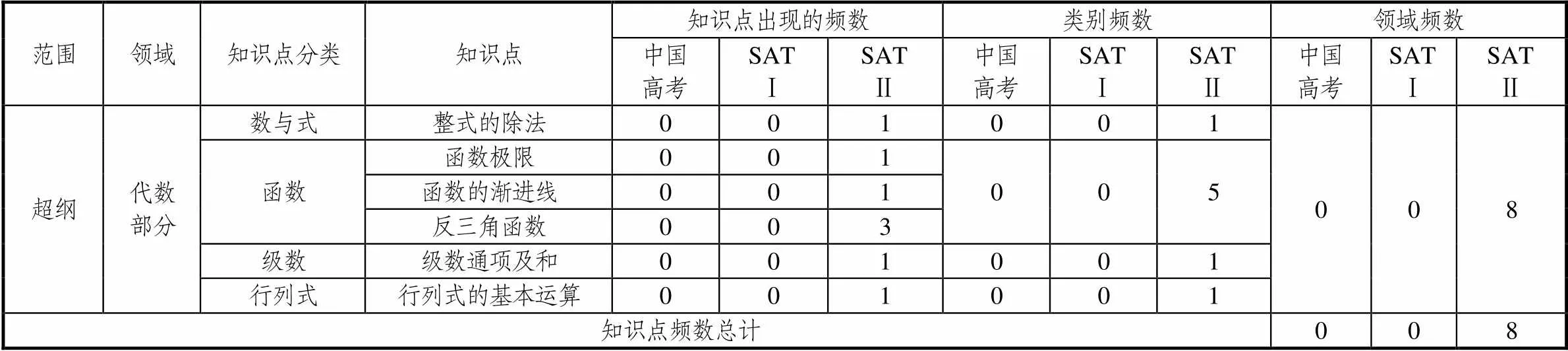
表3 超纲范围知识点分布情况

图1 3份试卷知识范围对比

图2 3份试卷知识领域对比

由图1、2可知，中国高考命题严格遵循大纲，没有仅考查初中知识或超纲试题．SAT Ⅰ试题超六成考查普通人需要掌握的初中重要知识，无超纲内容．充分体现SAT Ⅰ面向大众考生，知识的基础性占其主导地位，重视学生应用数学意识和适应未来大学学习基础的考查，不过多考虑试卷的区分度，这与美国选拔人才的多元化和大学的普及程度高有一定关系．SAT Ⅱ试题有11.59%知识点超出中国大纲，如级数、行列式等，为美国中学的大学先修课程内容，考查目的是了解学生高中数学学习达到的最高水平．数学SAT Ⅱ与SAT Ⅰ相比，更注重学生学科专业能力，名校和对数学能力要求高的专业在录取学生时较看重SAT Ⅱ成绩．美国中学开设了大学先修课程，学生由兴趣及未来需要自愿选择，内容包括微积分等大学知识．中国《普通高中数学课程标准（2017年版）》（简称新课标）[13]中选修课程与美国中学的大学先修课程定位基本一致，为大学自主招生提供参考．但由于高考不涉及，教师和学生并不重视选修课程，高三常专注于复习，学生精力大多浪费在过多解题技巧上，忽视了广泛丰富的新知识学习，对优秀生的培养不利．

在知识领域分布上，SAT Ⅰ与SAT Ⅱ类似，其代数、几何、概率与统计内容权重依次递减，代数占绝大部分内容．这与美国中学数学教育弱化立体几何知识有一定关系．中国高考更重视几何的考查，几何知识占比最高，代数及概率统计依次递减．卷1共16道小题、7道大题，其中8道小题及4道大题考查几何知识，涉及立体几何和平面解析几何，试题内容更加多样，更容易考出深度，实现选拔功能．

3.2 试题难度

3.2.1 数学高考试题综合难度模型

3.2.2 各因素水平划分

例3 某群体中的每位成员使用移动支付的概率都为，各成员的支付方式相互独立，设为该群体的10位成员中使用移动支付的人数，=2.4，(=4)<(=6)，则=（ ）．（2018年高考理科数学全国卷Ⅲ第8题）

A．0.7 B．0.6 C．0.4 D．0.3

分析：此题属于生活背景，无参数，简单符号运算，简单推理，大于等于3个知识点，顺向思维，运用水平试题．

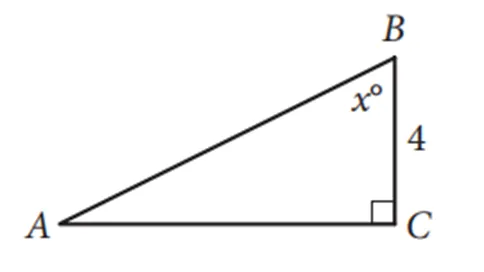
A．7 B．8 C．9 D．无法确定

分析：此题属于科学背景、无参数、简单符号运算、简单推理、单个知识点、顺向思维理解水平的试题．

对3份试卷所有题进行因素水平划分，统计各因素不同水平的考查情况，得到3份试卷各因素水平的比重．

表4 3份试卷水平划分汇总表

3.2.3 各因素难度

（1）背景因素．

由图3，卷1与卷3对背景因素考查相似，无背景题目占比最大，均占题目总数近八成，试题大多就数学知识本身展开，表征方式较抽象．卷2接近总数一半的题目基于生活背景，体现SAT Ⅰ试题背景较丰富，贴近生活．SAT Ⅰ面向大众考生，更注重数学基础知识和基本能力，而解决现实生活中基本数学问题能力是数学学习的基本能力，较多SAT Ⅰ数学试题考查生活情景中解决问题的基本能力．SAT Ⅱ重视数学学习高阶能力和更深层次数学知识的考查，更深层次意味着更抽象，常与生活情景相脱离．中国高考注重选拔人才，出于高区分度要求，需要考出一定深度．应将SAT Ⅰ、SAT Ⅱ两个方面的特点有机结合，正确处理考试深度和难度与基础和情境的关系．卷2和卷3科学背景水平占比均高于卷1，卷2最高，美国两卷尤其是SAT Ⅰ，更倾向于数学图形与图象的问题表征方式或与其它学科的联系，而中国高考试题对数学图形图象的考查偏弱，与其它学科联系不足．数学图形与图象是数学的语言，用数学语言表达，进而解决问题至关重要，需要在教学和考试中引起重视．

图3 背景因素不同水平变化折线对比

（2）是否含参．

由图4，卷1与卷2是否含参具有一定程度的一致性，但卷3与前两者差异较大，无参数水平占比约为前两者的1.3倍，占比90%，与SAT Ⅱ相比，中国试题与SAT Ⅰ试题相对更加注重对含参的考查．

图4 参数因素不同水平变化折线对比

（3）运算水平．

由图5，运算水平在3份试卷中呈现出较大差异．卷1简单数值计算和复杂数值计算水平试题合计约占试题总数的四分之一，简单符号计算和复杂符号计算水平试题合计约占四分之三，符号计算使试题计算难度加大，体现中国试题重视学生的运算能力，考查程度较深．卷2试题的运算水平大多停留在简单数值计算，简单数值计算水平试题占比接近八成，约为其余两卷的4倍．卷3关于4个水平的比例分布较均衡．中国高考和SAT Ⅰ都呈现复杂数值计算占比小，简单符号计算占比最高．

图5 运算因素不同水平变化折线对比

（4）推理能力．

由图6，简单推理试题在3份试卷中占比均高于50%，大部分试题利用“通式通法”即可解决，复杂推理水平试题相对较少，体现试题基础性是各类考试都需要考虑的方面．卷1推理两个水平题目占比差距不大，总体较均衡，推理水平难度适中．卷2简单推理水平占比超八成，复杂推理水平考查少．卷3两个水平都居中．由此可见，SAT Ⅰ偏重考查简单推理，属于合情推理，与SAT Ⅰ考查目的相符．而中国高考相当一部分试题更加侧重于考查复杂推理，对学生的逻辑推理能力要求较高．SAT Ⅱ处于两者之间．

图6 推理因素不同水平变化折线对比

（5）知识含量．

由图7，卷2与卷3对知识含量的考查相近，而卷1与其它两卷有较大差异．卷1知识含量前两个水平占比相同，其和超过50%，第三个水平占比接近50%．中国高考数学既重视基础试题的考查，也重视综合应用复杂试题的考查，能够清晰地划分学生掌握知识的能力，体现区分度．卷2超八成题目属于单个知识点水平，3个水平试题占比依次递减，说明大部分美国SAT Ⅰ试题知识含量较单一，较少综合考查知识的试题，对于难题考查不足，无法确切考查学生的综合应用能力水平．卷3中3个水平试题数量也依次递减，在3份试卷比较中仍处于中间地位．美国两卷对单个知识点水平的考查占比相近，超过或接近70%．

图7 知识含量不同水平变化折线对比

（6）思维方向．

由图8，卷1重视逆向思维的考查，重视学生对问题的灵活分析与解决．卷2偏重顺向思维，解题具有直接性．卷3对于顺向思维和逆向思维的考查无明显差异，两种水平较均衡，在3份试卷比较中也处于中间地位．

图8 思维方向不同水平变化折线对比

（7）认知水平．

由图9，卷1认知因素3种水平占比基本持平，说明中国高考对于数学认知的考查较全面，3个水平分布均匀，与美国两卷相比，分析水平占比最高．卷2理解水平占比近60%，运用和分析水平的题目占比依次降低，体现SAT Ⅰ注重基础，着重考查学生的基本认知．卷3运用水平占比最高，超50%，体现SAT Ⅱ重视知识的运用，有一定深度．

图9 认知因素不同水平变化折线对比

3.2.4 试卷整体难度

由模型公式计算出3份试卷各因素综合难度系数和整卷综合难度系数（见表5），由表5可以得到图10．

表5 3份试卷不同因素综合难度系数及总难度系数

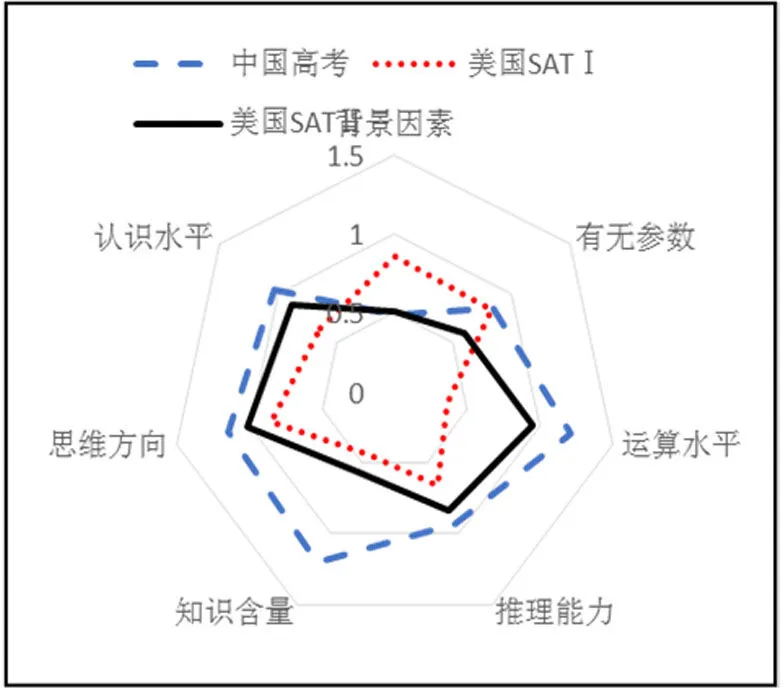
图10 各卷不同因素综合难度系数雷达图

由图10，背景因素方面，SAT Ⅰ难度较高，中国高考与SAT Ⅱ难度相近，都较低．含参方面，中国高考与SAT Ⅰ难度接近，高于SAT Ⅱ难度．在运算水平、推理能力、知识含量、思维方向、认识水平上，中国高考均最难，SAT Ⅰ最易，SAT Ⅱ居中．由表5，综合难度方面，中国高考难度较大，SAT Ⅱ次之，SAT Ⅰ相对容易．中美数学教育理念和高考功能很大程度上影响了两国数学考试的命题．基于现行中国高考制度，高考成绩完全决定了学生进入怎样的大学，为更好地实现其选拔功能和公平性，中国高考需确保区分度，因此相当一部分试题难度较大．美国教育更注重教育的层次性，既有面向大众的普通高等教育，又有面向优秀生的精英高等教育，不同层次学生都在自己的定位下有充分的选择和发展空间．SAT Ⅰ面向大众考生，更加重视生活中应用数学的基础能力，确保学生掌握生活中必备的数学技能和大学学习基础，对于学生的区分还可参考其它申请资料．SAT Ⅱ成绩是申请美国名校的依据之一，与SAT Ⅰ相比，难度有所提升，更能检验出学生的高阶数学能力．

3.3 数学核心素养

依据《普通高中数学课程标准（2017年版）》[13]确定的数学核心素养内涵，对3份试卷试题考查的数学核心素养进行标定．

例5 如图所示，表示汽车处于静止状态时轮胎侧面一点的标记．当汽车启动后（轮胎开始旋转），会经历一段时间的加速运动．下列哪一选项能够描述标记与地面的距离变化（ ）．（2019年SAT Ⅰ数学试题第41题）

分析：该题主要考查函数图象与函数模型应用．考生需要想象汽车启动后标记的位置的变化情况，并将以上情境与函数模型相联系，理解情境中时间与距离之间的对应法则，推理得出随着时间的推移标记与地面的距离变化情况，最终建立与之相适应的函数模型．解题过程中，考查了直观想象、数学抽象、逻辑推理、数学建模核心素养．

（1）证明：平面⊥平面；

（2）当三棱锥-体积最大时，求：面与面所成二面角的正弦值．

分析：该题综合考查立体几何与空间向量方面的知识．第一问，学生需要回忆面面垂直的判定定理，分析该题的具体条件，结合线线垂直、线面垂直的知识进行推理与证明，考查了数学抽象、直观想象和逻辑推理核心素养．第二问可通过建立空间直角坐标系，利用空间向量知识求解二面角的正弦值，伴随着运算与推理，考查了数学抽象、直观想象、数学运算及逻辑推理核心素养．

统计各卷考查数学核心素养的情况，得出3份试卷核心素养权重汇总表（见表6）和柱形图（见图11）．

表6 数学核心素养权重汇总表

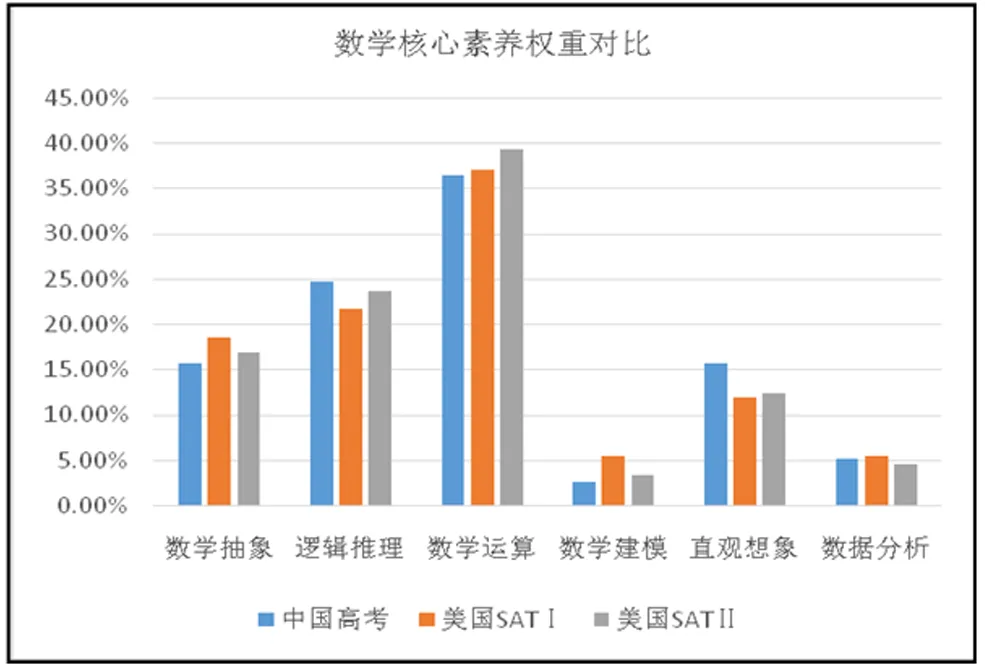
图11 3份试卷数学核心素养权重对比

（1）3份试卷权重最大的都是数学运算，其次是逻辑推理．新课标指出，“数学运算是解决问题的基本手段”“逻辑推理是数学严谨性的基本保证”[13]．SAT试题运算难度都不大，大量基础题列出算式作简单运算后即可获得答案，常常只考查了数学运算素养．中国高考试题往往涉及大量且复杂的运算，数学运算常贯穿整套试卷．

（2）数学建模权重在3份试卷中都较小，相对SAT Ⅰ最大．数学建模素养强调在现实情境中发现、分析及解决问题的能力，其内涵表达出3层含义：一是将现实问题抽象为数学问题，二是用数学语言描述现实问题，三是用数学方法构建数学模型解决问题．中国高考数学大多数试题缺乏现实情境，不满足数学建模素养内涵的第一层含义，因此数学建模素养权重较低．而SAT Ⅰ数学情境丰富多样，为数学建模素养的培养提供了很好的情境，这也是SAT Ⅰ数学建模素养占比在3份试卷中最高的原因之一，但其占比和水平仍较低，其试题往往直接给出关于问题的模型以考查学生对于模型的认知，忽视了学生独立构建模型环节．

（3）3份试卷对于数据分析素养的考查较少．这源于涉及数据分析素养的概率统计内容在中美高中数学教学中占比都小．在信息时代，日常生活和工作常面临数据分析的情境，合理分析数据至关重要，为了很好地解决问题，需要有良好的数据分析素养，应当加强学生数据分析素养的考查．

（4）3份试卷对于数学抽象素养考查权重较一致，在直观想象素养考查方面中国较高，这源于中国高考试卷中几何试题偏多．

（5）3份试卷对6个核心素养考查权重总体分布基本一致．尽管这6个数学核心素养及内涵是中国教育提出，但其反映的数学素养及数学能力却是各国数学教育都重视的方面．美国2010年颁布的《州共同核心数学标准》明确了数学素养的基本要义：有问题意识，并能坚持不懈地解决问题；抽象、量化地思考；构建切实可行的论证，评判他人的推理；构建数学模型；策略性地使用工具；关注精确度；在重复的推理中，探求并表达规律[15]．美国数学教育中数学素养内涵与中国新课标中6个数学核心素养内涵基本一致，反映的本质相同．

3.4 试题情境

在综合难度模型的比较中，从试题难度角度仅将背景因素分为3个水平，仅有“生活背景”这一水平描述现实情境．美国SAT试题情境丰富多样，仅使用“生活背景”进行概括不足体现其情境范围之广，PISA数学重视广泛丰富的试题情境考查．新课标强调“考试试题的任务情境要与社会生产生活、科技发展紧密相连，增强对学生综合应用数学知识解决实际问题能力的考查”[13]．在高考数学中引入类似PISA数学测试丰富的情境，有利于贯彻新课标理念．值得从PISA测试情境分类及内涵分析比较中美两国试卷．

依据文[16]PISA测试情境分类及内涵，对3份试卷的试题情境进行划分，分别得各卷试题情境分布表，进而得到3份试卷情境权重汇总表．

表7 3份试卷情境权重汇总

（1）科学情境（含纯数学情境）在中国高考和SAT Ⅱ中占比都超过85%，其试题多为纯数学问题，这与两卷均要考查学生较高数学水平有关．而SAT Ⅰ重视学生的数学基本能力和水平，重视学生日常工作生活中应用数学的意识和能力，其它3个情境占比接近50%．

（2）SAT Ⅰ对PISA中4种情境类型均有所涉及，而中国高考与SAT Ⅱ未覆盖所有情境类型．中国高考未涉及“个人情境”；SAT Ⅱ未涉及“职业情境”，另两卷的职业情境占比低于5%．这源于PISA测试主要考查学生是否具备未来进入社会所需知识、技能和数学素养，而中美高考的测试目的与PISA的测试目的不完全相同．

4 研究结论与启示

4.1 研究结论

4.1.1 关于试题内容

在知识领域方面，SAT Ⅰ与SAT Ⅱ类似，代数知识占绝大部分内容，几何、概率与统计内容依次减少．中国高考更加重视几何知识的考查，几何知识占比最高，代数及概率统计知识权重依次递减．3份试卷对于概率与统计领域知识的考查均较少．在知识范围方面，中国高考数学试卷没有只考查初中知识或超纲试题．SAT Ⅰ试卷超过六成考查初中知识，多数是普通人需要掌握的初中重要知识，无超纲内容．SAT Ⅱ试卷有11.59%的知识超出中国高考大纲，均为大学内容．

4.1.2 关于试题难度

（1）背景方面，中国高考与SAT Ⅱ大多为无背景试题，SAT Ⅰ试题生活背景居多，SAT Ⅰ更偏向于利用数学图形、图象表征数学问题．

（2）含参数方面，3份试卷均呈现出无参数试题少于有参数试题，中国高考与SAT Ⅰ情况相近，而SAT Ⅱ在含参数的考查上较弱．

（3）运算水平方面，3份试卷呈现出较大差异，中国难度最大，运算水平大多为符号计算，SAT Ⅰ试题多停留在简单数值计算水平，难度最小，SAT Ⅱ试题对4个水平的考查较全面均衡．

（4）推理能力方面，SAT Ⅰ简单推理试题相对偏多，中国高考推理两个水平考查较均衡，SAT Ⅱ介于其它两卷之间．

（5）知识含量方面，中国高考既有单一知识点试题，也有综合应用试题，后者较多，美国两卷整体相近，试题大多知识含量单一，对综合应用试题的考查不足．

（6）思维方向上，中国高考逆向思维试题较多，常间接求解，而SAT Ⅰ顺向思维试题偏多，解题具有直接性，SAT Ⅱ情况介于其它两卷之间．

（7）认知因素方面，中国高考对于数学认知的考查较全面，SAT Ⅰ着重考查学生的基本认知，SAT Ⅱ重视知识在不同情境下的运用．

（8）关于试题综合难度，中国高考难度较大，SAT Ⅱ次之，SAT Ⅰ相对容易．在背景因素上，SAT Ⅰ难度最大，另两卷难度相近，均远小于SAT Ⅰ．在含参数方面，中国高考与SAT Ⅰ难度相近，均高于SAT Ⅱ．在运算水平、推理能力、思维方向、知识含量及认识水平因素上，各因素的难度均为中国高考最难，SAT Ⅰ最易，SAT Ⅱ居中．

4.1.3 关于数学核心素养

在每份试卷中数学运算权重均最大，逻辑推理次之，数学建模及数据分析权重都较小，SAT Ⅰ这两种核心素养权重比其它两卷高．3份试卷数学抽象权重基本一致，直观想象权重中国高考最高．3份试卷对各素养考查分布总体情况基本一致，这源于中美两国数学素养的内涵基本一致，体现了数学素养的国际化．

4.1.4 关于试题情境

3份试卷占比最大的均为科学情境（含纯数学情境），中国高考与SAT Ⅱ占比都超85%．SAT Ⅰ包含PISA中4种类型情境，与PISA测试中的情境匹配程度最高，较重视对试题情境的考查；中国高考缺失“个人情境”，对学生实际生活中解决问题的能力考查不足；SAT Ⅱ缺失“职业情境”，另两卷对“职业情境”的考查都未达4.5%．

4.2 研究启示与建议

由于中美两国文化背景、国情的不同，中国数学教育只能部分借鉴美国教育与考试机制，取其精华，探索出适合中国国情、有中国特色的教学与高考改革道路．

（1）重视选修课程的学习，贯彻因材施教原则．

美国高中数学教育较好地设计了大学先修课程，SAT Ⅱ对其内容进行了考查，不仅使学有余力的学生掌握更深层、更丰富的数学知识，促进卓越发展，而且考生能够通过SAT Ⅱ展示自己的实力，利于名校对优秀生的录取，利于理工科优秀人才选拔．中国新课标对选修课程已有较好安排，中共中央、国务院印发《深化新时代教育评价改革总体方案》[17]提出有序推进选课走班，进一步落实需要各级教育部门具体政策支持和学校评价的驱动，也需要高考制度的改革引导，真正落实不同学生能获得不同发展，彰显学生个性．

（2）积极创设问题情境，激发学生数学学习内生动力．

SAT Ⅰ数学重视问题情境的设置，情境丰富多样，覆盖了日常生活中的诸多情况，缩小了学生与数学的距离，有利于培养学生应用数学意识和学习数学的兴趣．中国高考数学应适当增加试题情境的多样性，将数学融入实际生活等现实情境，引导中学教师在教学中以学生的直接经验为基础，积极创设贴近生活实际的情境，将思想政治教育元素融入情境和教学，让学生感受数学的实用性，激发学生数学学习的内生动力，发挥高考数学命题的立德树人和教学导向功能．

（3）深化高考制度改革，重视学生综合素质评价．

美国两卷难度较低，而由于区分度的要求，中国卷多数题目均有一定的难度，对学生的思维水平和知识储备有较高要求，但相当一部分学生还达不到这种要求．在针对高考的各种复习考试中数学成绩低，打击了这些学生学习数学的信心，不利于发挥数学教育育人功能．需要通过高考制度的深入改革，将终结性评价与过程性评价相结合，重视学生高中学业成绩、班级排名、推荐信、课外活动、文体才能等能判断学生综合素质的情况，减轻高考数学对学生的心理压力，增强学生学习数学信心．文[17]提出“逐步转变简单以考试成绩为唯一标准的招生模式”的要求，目前“统一高考”“高中学业水平考试”“综合素质评价”的综合评估大学招生机制已在高考改革的探索阶段，如何保证其公平性仍是教育必须面对的问题，需要不断探索加以完善．

（4）加强数学建模与数据分析素养考查，提高学生应用数学解决问题能力．

现实世界对通过数据分析和数学建模解决现实问题的需求不断增强，数据分析与数学建模素养至关重要，加强数学建模与数据分析素养的考查有利于一线教学对培养学生在现实世界发现问题、分析及解决问题能力的重视．中国高考应增加在现实情境中构建模型、分析真实数据的试题．

（5）组织多次考试，科学设置自主考试．

针对中国目前高考现状，每位学生仅有一次参加高考的机会，学生成绩存在偶然因素的影响，选拔人才相对不够科学[18-21]．美国大学入学考试有多种形式，且每种考试有多次参加机会，学生有多种选择充分发挥其真正水平，弱化一次考试中偶然因素的影响，减轻学生压力．此外，为适应不同水平学生对未来大学专业和职业选择，使优秀生能够发挥出其水平，在高考的基础上，可通过大学自主考试等形式，更多考查选修课程内容，使不同水平学生获得不同发展，这方面，新开启的强基计划将有新的尝试．

[1] 谢晓川，方浩颖，陈楠，等．中英高考数学试题比较研究[J]．中学数学研究，2019（10）（上）：12-14．

[2] 武小鹏，张怡．中国和韩国高考数学试题综合难度比较研究[J]．数学教育学报，2018，27（3）：19-24．

[3] 李保臻，石烨．中国大陆与台湾地区高考数学试题难度比较研究——以2016—2018年大陆全国卷Ⅰ与台湾指考试题为例[J]．数学教育学报，2020，29（1）：58-64．

[4] 张玉环，周侠．综合难度视角下中法高考数学试题的比较研究——基于2015—2019年中国和法国高考数学试卷[J]．数学教育学报，2020，29（3）：43-50．

[5] 鲍建生．中英两国初中数学期望课程综合难度的比较[J]．全球教育展望，2002，31（9）：48-52．

[6] 石凤雪．美国SAT数学考试对我国高考改革的启示[J]．吉林省教育学院学报，2017，33（2）：141-144．

[7] 马玮．2008年美国SAT试题与上海高考试题的比较[J]．数学教学，2009（11）：39-41．

[8] 黎郭凯．2017年美国SAT试题数学部分与全国高考理科乙卷试题的比较分析[J]．中学数学杂志，2018（5）：28-30．

[9] 王奋平．美国高考及其数学考题特点浅探[J]．中学数学教学参考，2008（9）：55-57．

[10] 刘思庄．SAT 数学试题和高考数学试题的比较分析[J]．科技创新与生产力，2018（10）：22-25．

[11] 教育部考试中心．2019普通高等学校招生全国统一考试大纲（理科数学）[EB/OL]．（2019-01-31）[2020-01-12]．http://www.neea.edu.cn/html1/report/19012/153-1.htm．

[12] 中华人民共和国教育部．义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2011：12-20．

[13] 中华人民共和国教育部．普通高中数学课程标准（2017年版）[M]．北京：人民教育出版社，2018：4，80-89，100-106．

[14] 武小鹏，孔企平．基于AHP理论的数学高考试题综合难度模型构建与应用[J]．数学教育学报，2020，29（2）：29-34．

[15] 范文贵，李伟华．美国《州共同核心数学标准》解读[J]．天津师范大学学报（基础教育版），2012，13（2）：39-42．

[16] 黄华．从PISA数学素养测试对国内数学教学的启示——PISA数学素养测试与上海市初中毕业统一学业考试数学测试之比较[J]．上海教育科研，2010（5）：8-11．

[17] 中共中央国务院．深化新时代教育评价改革总体方案[EB/OL]．（2020-10-13）[2020–10–25]．http://www.gov.cn/zhengce/2020-10/13/content_5551032.htm．

[18] 史宁中，吕世虎，李淑文．改革开放四十年来中国中学数学课程发展的历程及特点分析[J]．数学教育学报，2021，30（1）：1-11．

[19] 任子朝，赵轩，关丹丹，等．图形分析法在高考试题评价中的应用研究[J]．数学教育学报，2021，30（1）：37-41．

[20] 张玉环，周侠，陈爽．核心素养视角下中法高考数学试题的比较研究——基于2015—2020年中国和法国高考数学试卷[J]．数学教育学报，2021，30（1）：42-48．

[21] 武丽莎，朱立明．高中数学学科核心素养：生成机制与培养路径[J]．数学教育学报，2021，30（4）：25-29．

Comparative Study of Mathematics Test Papers in College Entrance Examination between China and the United States

HAN Jin-xuan1, 2, YANG Ze-heng1, WANG Peng-de1

(1. Department of Mathematics and Computer, Dali University, Yunnan Dali 671003, China;2. Nankai Zhongying Primary School, Tianjin 300110, China)

SAT is a widely used college entrance examination in the United States. Similar to the Chinese college entrance examination, both of them have certain guidance for senior high school education. It is of certain significance to analyze and compare the mathematics test questions of both of them for the reform of Chinese high school and College Mathematics Education in China. Based on the national college entrance examination syllabus, comprehensive difficulty model, mathematical core literacy and PISA test situation, the comparison of SAT I, SAT II, and Chinese college entrance examination mathematics test questions shows that: SAT I and SAT II have the highest proportion of algebra, and China’s geometry has the highest proportion;SAT I exceeds 60% of the knowledge of junior high schools, and some knowledge of SAT II exceeds the syllabus of China’s college entrance examination. Comprehensive difficulty, reasoning ability and other factors were the most difficult in China, SAT I is the easiest, and SAT II is in the middle; SAT I background factors are the most difficult; China and SAT I are similar in the difficulty of parameters, but they are higher than SAT Ⅱ. The distribution of the three volumes of the core mathematics literacy test is generally consistent, and the weight of intuitive imagination is the highest in China. SAT I includes four types of situations in PISA, whereas China and SAT Ⅱ do not cover all types of situations in PISA. Some enlightenment is got such as teaching students in accordance with their aptitude and stimulating students’ endogenous motivation.

comprehensive difficulty model; SAT mathematics test; mathematics test in college entrance examination; comparative study

2021–11–08

云南省教育厅教学改革项目——数学与应用数学专业学生实践能力培养体系建设的实践与研究（2013云南高校教改43）；云南省学位委员会研究生教学案例库建设项目——数学教育测量与评价研究生教学案例库（云学位〔2019〕17号（201））；2021年度云南省研究生优质课程建设项目——数学教育测量与评价（云学位〔2021〕12号（88））

韩金璇（1996—），女，天津人，硕士，小学教师，主要从事中小学数学教学研究．杨泽恒为本文通讯作者．

G424.79

A

1004–9894（2022）02–0013–08

韩金璇，杨泽恒，王彭德．中美高考数学试卷比较研究[J]．数学教育学报，2022，31（2）：13-20．

[责任编校：张楠、陈汉君]