考虑极限场景的并网型微电网分布鲁棒优化方法

曹金声，曾 君，刘俊峰，薛 峰

（1. 华南理工大学电力学院，广东省 广州市 510640；2. 广东省绿色能源技术重点实验室（华南理工大学），广东省广州市 510640；3. 华南理工大学自动化科学与工程学院，广东省 广州市 510640；4. 广东电网有限责任公司东莞供电局，广东省 东莞市 523009）

0 引言

近年来，为了解决全球环境污染与能源危机问题，微电网凭借其高效性、灵活性、环保性得到了迅速发展［1］。然而，随着负荷多样性与可再生能源渗透率不断提高，这些随机性给微电网的运行优化带来了巨大挑战［2］。如何合理进行不确定环境下的并网型微电网运行优化，是目前亟待解决的关键问题。

针对源荷的不确定性，目前方法主要包括随机优化（stochastic optimization，SO）、鲁棒优化（robust optimization，RO）和分布鲁棒优化（distributionally robust optimization，DRO）。SO 采用准确的概率分布描述不确定量，模型简单、求解速度快［3-4］。SO 需要提前假设随机变量的概率，但假定的概率分布具有主观性。RO 无须假定概率信息，常用于处理微电网不确定问题［5-6］。然而RO 研究最差场景的优化问题，保守性较高。DRO 由Scarf 于1958 年提出，利用随机变量的统计分布信息建立不确定集合，既考虑了概率分布特征，又避免了过高的保守性［7］。DRO 的关键难点在于不确定集的建立。文献［8］利用风电历史场景构建矩不确定集，利用DRO 进行调度决策，文献［9］采用基于KL（Kullback-Leibler）散度的DRO 研究热泵储能参与的日前经济调度问题；文献［10］中构造了风电功率的矩不确定集，研究了配电网的分布鲁棒实时调度方法。基于矩信息的DRO 会导致不确定集包含与真实分布差距很大的概率分布函数［11］，且计算比较繁琐；而基于概率距离的DRO 通过描述经验概率分布与其他分布之间的距离，构造出基于概率距离的概率分布模糊集［12］，该方法能充分发挥数据的统计特征，样本外表现较好［7］。常用的概率距离为Wasserstein 距离，该距离具有对称性，并且不含非线性，便于计算［11］。基于Wasserstein 距离的DRO 在日前优化领域已有研究［13-14］。但是，该方法需要转化为基于场景的优化问题进行求解，其计算规模随场景数量的增加而增大。对于微电网运行优化，随机变量个数较多、场景集规模较大，如何削减场景数量，构建合适的概率分布模糊集是DRO 的关键。

针对微电网运行特性，本文将极限场景法融入DRO 的场景处理中。极限场景集由于包含随机变量的所有取值空间，可以减少模糊集中样本的个数，优化求解时间［15］。文献［15-16］证明了极限场景法在线性规划问题和二次约束问题下的合理性。文献［17］利用极限场景处理含随机变量的配电网无功优化问题。文献［18］提出了一种考虑风光负荷极限场景的配电网鲁棒规划方法。可见，极限场景法结合DRO 是可行的。

鉴于此，本文充分考虑并网型微电网的不确定性以及微电网与配电网之间的相互影响，针对并网型微电网的运行优化问题，提出考虑极限场景的DRO 方法。本文的主要创新点在于：

1）充分考虑微电网与配电网利益诉求的互斥性，建立双层运行优化模型。其中，微电网模型是考虑源荷不确定性的DRO 问题，配电网模型是计及网损的凸优化问题，并采用目标级联分析法（analytical target cascading，ATC）实现联合优化。

2）在建立概率分布模糊集时融入极限场景的思想。构造基于Wasserstein 距离的概率分布模糊集，并利用极限场景修正该模糊集，以提升模糊集的鲁棒性，避免场景集过大，提高求解效率。

1 并网型微电网运行优化基本架构

1.1 典型架构和交互机制分析

并网型微电网整体架构见图1。微电网并网运行，微电网与配电网之间通过联络线进行电量交易。其中，微电网包括光伏设备、柴油发电机、储能装置和多种类型负荷，配电网具备主网供电和相应负荷。微电网与配电网均以最小化日前运行成本为目标，联络线上具有传输功率相等的一致性约束，因此存在利益冲突且耦合性较强，只考虑微电网的利益诉求是片面的，应对微电网和配电网进行综合考量。如何合理高效地处理微电网内部的源荷不确定性，如何处理整体架构下联络线约束的耦合性是本文需要解决的问题。因此，本文利用极限场景建立概率分布模糊集，采用ATC 处理整体架构的强耦合性。

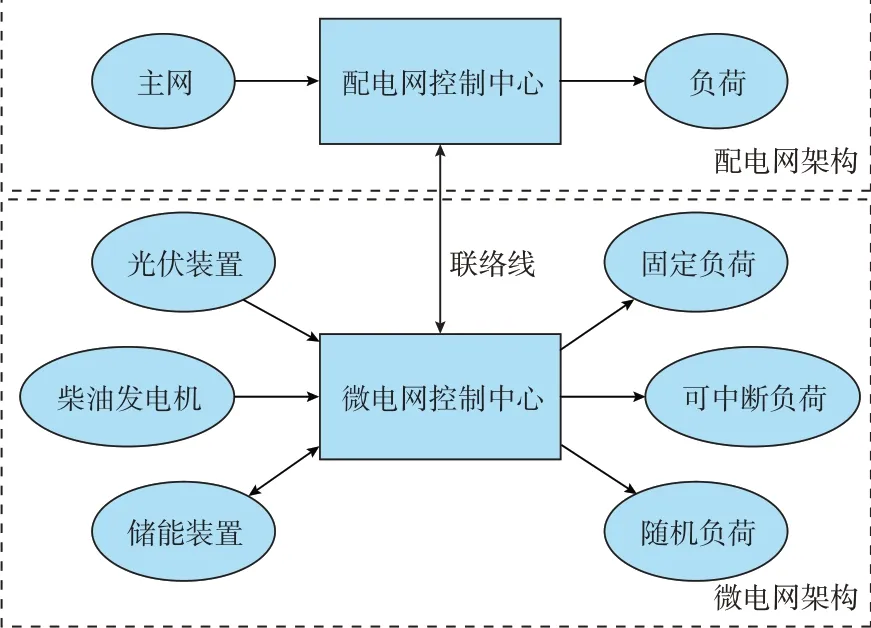
图1 系统整体架构Fig.1 Overall system framework

1.2 考虑源荷不确定性与极限场景的概率分布模糊集

微电网在实际运行中易受到许多不确定因素的影响。本文采用基于Wasserstein 距离的DRO 建立模糊集并结合极限场景法构造场景集，以提高模型的鲁棒性与求解效率。以城市光储型微电网为例，本文所考虑的不确定量为光伏发电量与随机负荷的用电量。

考虑负荷与光伏出力的不确定性，定义随机变量ξ̂，其中ξ̂j表示ξ̂的第j（j=1，2）行元素，ξ̂1为负荷的历史观测数据，ξ̂2为光伏发电的历史观测数据。对于第j 行不确定量，根据历史观测数据ξ̂j，1，ξ̂j，2，…，ξ̂j，N（N 为样本总量），并利用狄拉克分布构造ξ̂j的参考分布P̂N［19］。参考分布可以看作对真实分布的估计，为了表示真实分布与参考分布之间的差距，引入Wasserstein 距离：

式中：P(·)为求概率函数；S 为Ω2的直径，它定义了Ω2中任意一对元素之间的最大Wasserstein 距离；β取值0 到1，表示实际样本处于Wasserstein 球内的概率，β 越大则概率越大，同时为了保持一定的冗余度，本文中β 取值为0.95。

从式（4）可以看出，ε 随样本量的增大而减小，当样本量N 趋于无穷大时，ε 趋向于0，此时意味着真实分布与参考分布相同，DRO 退化为确定性的SO［12］。

极限场景定义为所有随机变量取得极值的情况。当随机变量维度为n 时，极限场景的个数［16］为2n，构成的极限场景集具有代表性，包含了随机变量的所有取值范围，因此可以极大减少场景集的个数。传统DRO 考虑的场景集主要为常规场景。本文将极限场景与DRO 相结合，构造具有更强鲁棒性的场景集，从而改善描述随机变量的概率分布模糊集，使其既能反映历史数据的分布情况，又可以兼顾极限场景带来的优势。建立模糊集的具体步骤如下：

1）记录N 组负荷历史数据ξ̂1，1，ξ̂1，2，…，ξ̂1，N，记录N 组光伏出力历史数据ξ̂2，1，ξ̂2，2，…，ξ̂2，N，利用这N 组数据，形成关于不确定量的参考分布P̂N，利用式（4）计算Wasserstein 半径ε1，构造Wasserstein 球。

2）建立随机变量的多面体不确定集，根据极限场景的定义，选择多面体的4 个顶点作为极限场景，令生成的4 个极限场景点分别为(ξ̂1，N+1，ξ̂2，N+1)、(ξ̂1，N+2，ξ̂2，N+2)、(ξ̂1，N+3，ξ̂2，N+3)、(ξ̂1，N+4，ξ̂2，N+4)，将这些极限场景数据加入原来的历史数据中，形成新的场景集。

3）由于极限场景具有代表性，一个极限场景对场景集的作用相当于数个常规场景的作用，根据式（4）利用新的场景集重新计算Wasserstein 半径ε2。

4）此时，新的场景集中包含常规场景与部分极限场景，其作用相当于大量常规场景构造的场景集，利用新场景集最终得到的分布鲁棒模糊集Dw如下：

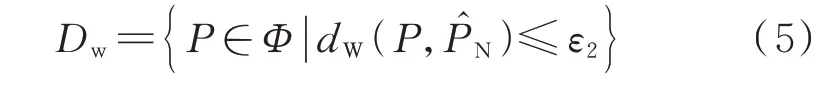
1.3 微电网运行优化模型

微电网在供电侧包括柴油发电机、配电网供电、储能装置与光伏设备，需求侧包括固定负荷、随机负荷与可中断负荷。微电网的目标函数是最小化日前运行成本，考虑到上文提到的源荷不确定性，微电网模型的目标函数主要包括柴油机发电成本、配电网购电成本、储能装置储能成本、可中断负荷补贴成本和光伏发电补贴成本［20］。目标函数具体如下：

微电网的约束条件主要包括功率平衡约束、柴油机出力约束、联络线功率约束、储能装置出力约束、可中断负荷约束与无功补偿器约束。

1）功率平衡约束

式中：QSVC，max和QSVC，min分别为无功补偿器补偿无功功率的上、下限。

1.4 配电网运行优化模型

配电网的优化目标为最小化日前运行成本，日前运行成本主要包括网损成本、主网购电成本、与微电网电量交互成本。其中，与微电网电量交互成本属于配电网的盈利成本［21］，具体如下：

配电网的约束条件包括潮流约束、供需平衡约束、联络线功率约束和无功补偿器约束，具体如下。

1）潮流约束

为了保证求解的速度与准确性，避免常规潮流计算中的平方项，本文采用Distflow 模型作为配电网潮流约束。

4）无功补偿器约束同式（12）。

2 模型求解

前文提出了并网型微电网的基本架构，该模型是包含微电网和配电网的双层运行优化模型，其中的微电网模型较为复杂，难以直接求解，所以本文首先对微电网模型进行对偶处理，然后对模型在联络线处进行解耦，采用改进ATC 对该问题进行迭代求解。下文将分别介绍微电网分布鲁棒问题的对偶处理与改进ATC 的应用。

2.1 微电网分布鲁棒模型的对偶处理

本文基于1.2 节构造的微电网模型可以描述为以下简洁形式：

式中：x 表示系统常量，包括固定负荷值和系统网络结构；ξ 表示随机变量，包括光伏出力值和随机负荷值；y(x，ξ)表示决策变量，包括联络线交互功率、储能装置充放电功率、柴油发电机出力、可中断负荷连接状态和无功补偿器补偿功率；dTy(x，ξ)表示目标函数值，如式（6）所示，其中d 为目标函数常系数矩阵；Ey(x，ξ)≤g(x，ξ)表示约束条件，如式（7）—式（12）所示，其中E 为约束条件的常系数矩阵；g 为约束条件的变系数矩阵。

微电网的目标函数是一个基于Wasserstein 距离的分布鲁棒问题，由于不确定量的随机性，该问题是一个半无限规划问题，难以直接求解。可以利用强对偶理论将原问题转换为以下确定性问题［22］：

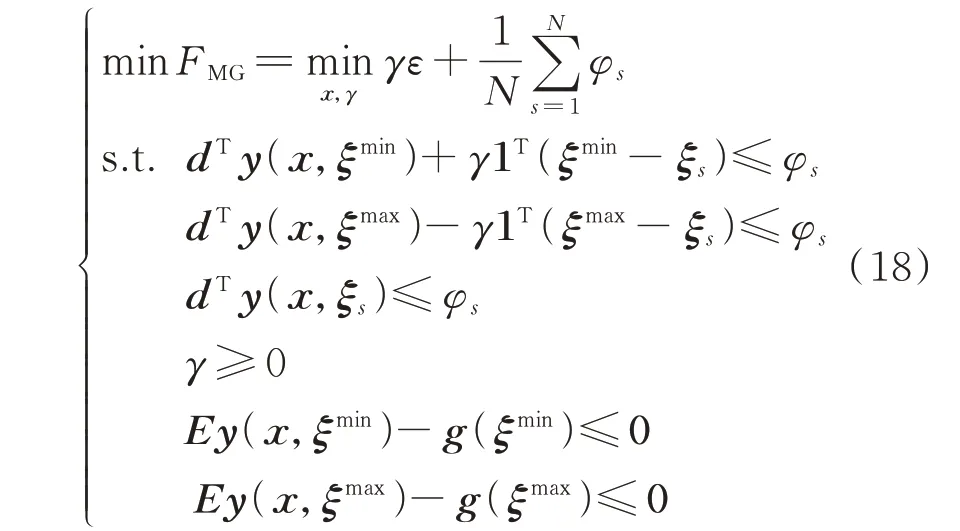
式中：γ 和φs为拉格朗日算子；ξs为随机变量；ξmin和ξmax分别为随机变量取得的最小、最大值。

2.2 改进ATC

ATC 常用于多主体系统的联合求解当中，它与交替方向乘子法（ADMM）类似，不仅是求解数学优化问题的工具，也是复杂系统分析建模的方法［23］。ATC 的主要思路是将复杂问题的目标函数与约束条件进行拆解，分解成若干个子问题，从而降低原问题的维度。对于本文建立的微电网与配电网双层优化模型，耦合约束是一致性约束形式。与ADMM相比，ATC 构造出的目标函数更为简洁，建模思路清晰，并且具有更强的收敛性［24］，可以高效地处理两者间的优化问题。

微电网和配电网的优化模型是强耦合的，在联络线位置存在如下的一致性约束，由于存在这个约束，所以很难将两者分开独立计算。

ATC 将该一致性约束作为惩罚项加入微电网与配电网各自的目标函数中，从而将一致性约束实现解耦，通过微电网与配电网的不断迭代，使得该约束最终得以实现。引入惩罚项的微电网目标函数可以表示为：

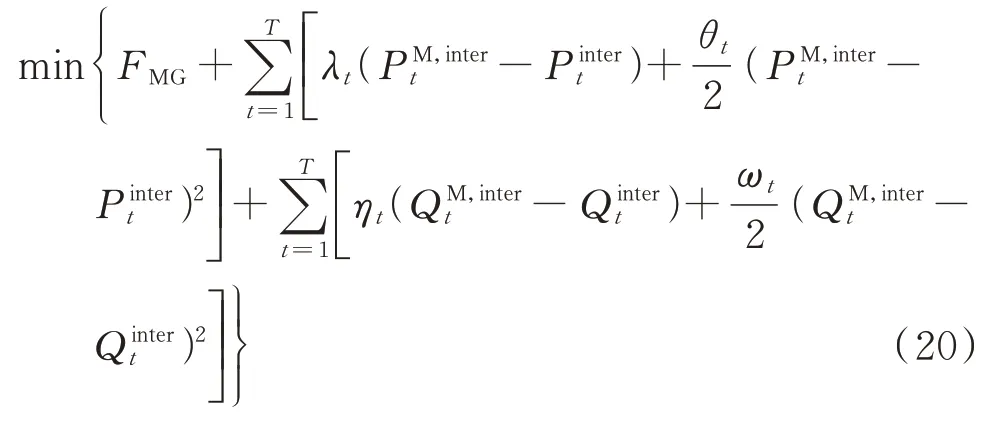
式中：λt、θt、ηt、ωt为ATC 算子。

同理，引入惩罚项的配电网目标函数可表示为：

为了加快ATC 迭代速度，在每次迭代更新之后，按照文献［25］中的方法不断更新ATC 算子。

2.3 算法步骤与流程图

综上所述，本文算法流程如图2 所示。本文的算法步骤包括构造概率分布模糊集与ATC 迭代求解两个部分，具体步骤如下：

图2 算法流程图Fig.2 Flow chart of proposed algorithm

步骤1：引入光伏与负荷的历史数据，构造原始Wasserstein 球。

步骤2：利用历史数据生成极限场景，加入原有的场景集当中。

步骤3：修正原始Wasserstein 球的半径，使其包含新的数据集中的所有数据，形成考虑源荷不确定性与极限场景的概率分布模糊集。

步骤4：初始化配电网与微电网的网络信息、联络线信息与ATC 算法参数。

步骤5：接收联络线信息，求解配电网运行优化问题，将联络线信息传输给微电网。

步骤6：接收联络线信息，求解微电网运行优化问题，将联络线信息传输给配电网。

步骤7：判断是否满足收敛条件。若满足，结束迭代，输出优化结果，否则更新ATC 算子，重复步骤5 到步骤7。

3 算例分析

为了验证本文所提模型与方法的有效性，利用MATLAB R2018a 进行仿真，运用商用求解器GUROBI 求解模型，所有操作均在Windows 10 系统，CPU 为Intel Core i5 2.4 GHz，RAM 为8 GB 的计算机上实现。本文配电网算例采用改进IEEE 33节点系统，微电网算例采用13 节点系统，两系统通过联络线连接，如图3 所示。其中，微电网的3 组负荷分别表示固定负荷、随机负荷与可中断负荷。配电网的额定电压为220 V，线路电阻为0.152 4 Ω/km，电抗为0.050 8 Ω/km，平衡节点选择节点1。微电网包含光伏设备、柴油发电机组、储能装置、负荷、无功补偿器与联络线节点。配电网与微电网的光伏数据、负荷数据与分时电价数据参考文献［2］，Wasserstein 球置信度选为0.95，ATC 迭代参数参考文献［19］，ATC 收敛判据参数τ1、τ2、τ3分别取为0.1、0.005、0.5。

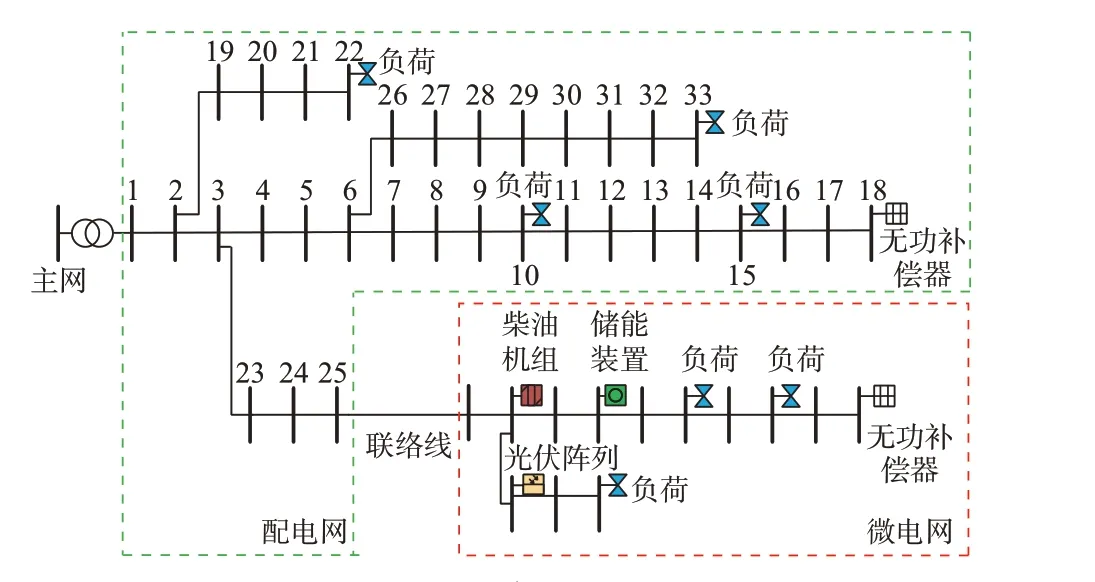
图3 系统仿真图Fig.3 Diagram of simulation system

3.1 日前优化结果

根据本文所提并网型微电网运行优化模型，采用改进ATC 进行求解，在蒙特卡洛法生成的一个常规场景下进行仿真，该场景的光伏、负荷数据均符合常规水平，均在可能出现的范围之内，最终得到配电网与微电网的运行优化结果，分别见图4 和图5。

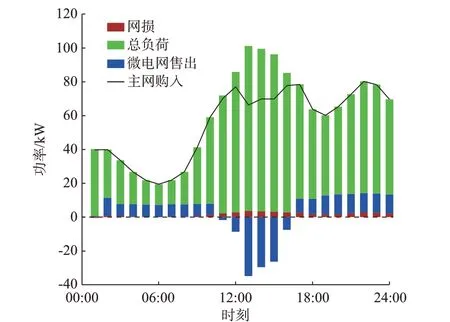
图4 配电网优化结果Fig.4 Optimal results of distribution network

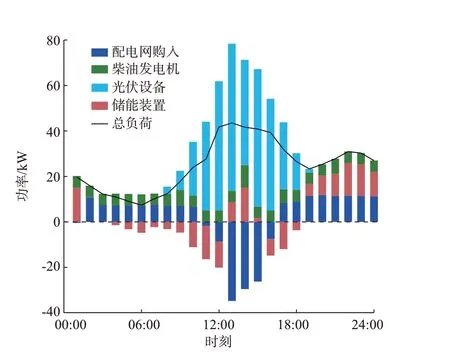
图5 微电网优化结果Fig.5 Optimal results of microgrid

由于配电网与微电网是协同优化的，所以图4中配电网流入微电网的功率等于图5 中微电网从配电网购入的功率。图5 中储能功率的正负分别代表储能装置的放电与充电过程。通过分析微电网的优化结果可以得出：由于00：00—08：00 时段负荷量较小，柴油发电机按照最低发电量发电；在08：00—18：00 时段，受到光照强度的影响，光伏设备参与了微电网的功率调节，系统总发电量与总负荷量达到功率平衡；在10：00—18：00 时段，光伏发电在所有电源出力中占据了主导地位，此时微电网发电量过剩，并且由于该时段下电价较高，微电网将光伏发电多余的电量出售给配电网，并将一部分电量存储在储能装置中；在19：00—24：00 时段，负荷量有所减少，储能装置处于放电状态，与柴油发电机和配电网进行协同优化，实现日前运行成本最优。

收敛情况随迭代次数的变化如图6 所示。一开始由于ATC 参数的初值较小，系统的状态量随迭代次数的变化较大。随着迭代次数的增加，配电网与微电网日前运行成本逐渐达到平缓的状态。在迭代了13 次之后，系统满足收敛判据，最终的优化方案是配电网与微电网协同决策的结果。式（22）和式（23）中3 个收敛指标的收敛过程如附录A 图A1 至图A3 所示。集中优化与分布优化方案对比如附录B 图B1 所示，集中优化下，配电网日前运行成本为1 437.42 元，微电网日前运行成本为945.00 元。分布优化下，配电网日前运行成本为1 440.15 元，微电网日前运行成本为941.27 元。可见，经过多次迭代后，集中优化与分布优化结果差异较小，在配电网和微电网协同运行模型中，本文所用ATC 是有效的。

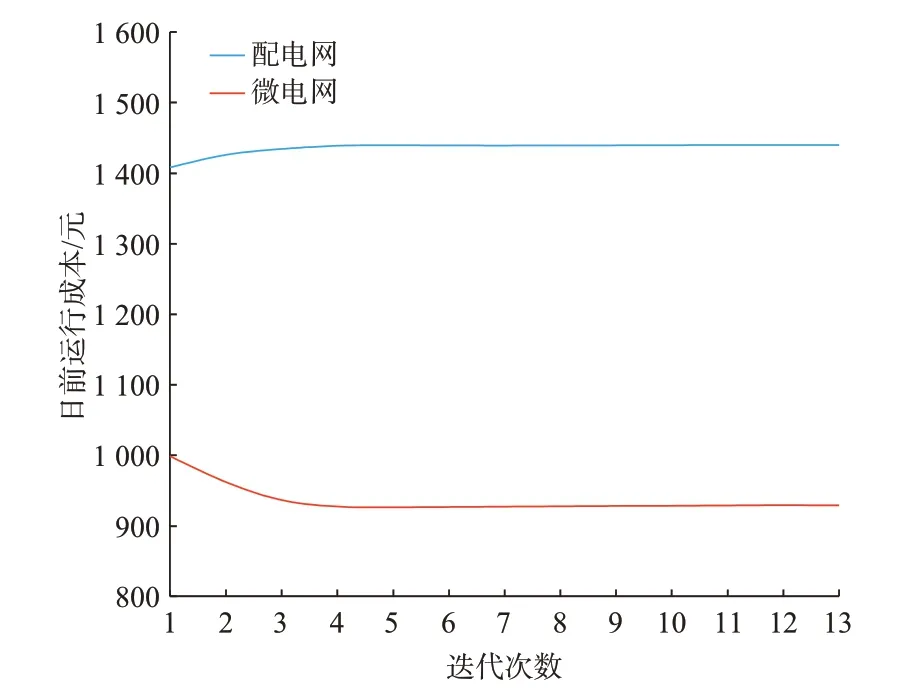
图6 算法收敛性分析Fig.6Analysis of convergence of proposed algorithm

3.2 不同RO 模型对比分析

本文提出了考虑极限场景的DRO 方法。为了体现该方法的优越性，本文所提方法与传统DRO 和传统RO 进行对比，传统DRO 模型采用的是基于Wasserstein 距离的DRO，分别在常规场景与极限场景下进行仿真，仿真数据均选自样本外数据。常规场景下的仿真结果如表1 所示。

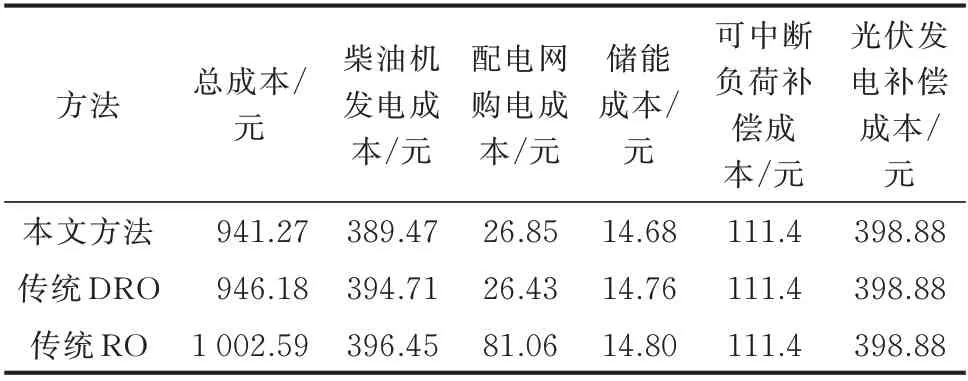
表1 常规场景下不同方法对比结果Table 1 Comparison results of different methods in conventional scenarios

本文随机生成了一组典型的常规场景，通过对比结果可以看出，在常规场景中，与传统DRO 相比，本文所提的考虑极限场景的DRO 具有降低日前成本的作用，与传统RO 相比成本节省了6% 左右。DRO 考虑了随机变量的统计分布特性，在场景数量较多时趋向于SO，故优化效果较好，本文所提方法在模糊集上考虑了极限场景的选择，具有更强的鲁棒性，传统RO 在优化过程只考虑最差场景的情况，所以该方法的保守性是最高的。综上所述，本文所提方法在常规场景下具有一定的优势。

此外，本文还采用4 种极限场景进行对比分析，分别为：极限场景1——光伏出力与随机负荷均采用最小值；极限场景2——光伏出力采用最小值，随机负荷采用最大值；极限场景3——光伏出力采用最大值，随机负荷采用最小值；极限场景4——光伏出力与随机负荷均采用最大值。极限场景下的仿真结果见表2。

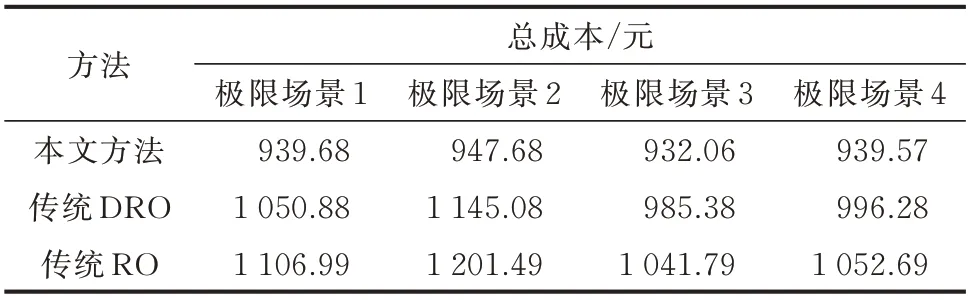
表2 极限场景下不同方法对比结果Table 2 Comparison results of different methods in extreme scenarios

通过对比可以得出，在4 种极限场景的验证下，基于极限场景的DRO 在构造不确定集时，考虑了极限场景出现的情况，因此效果表现较好，而传统方法只考虑常规场景，在极限场景下的效果大打折扣。因此，本文所提方法具有普适性，可以适用于实际的工程应用当中。

3.3 分布鲁棒模型与场景数量分析

由于微电网具备完善的历史数据存储功能，传统DRO 选择上百个场景较为合适。通过表3 可以得出，传统DRO 在选取500 个场景后，计算出日前总成本约为941.43 元，由于场景集过大，求解时间长达90 min，而本文所提方法在构造不确定集合时，人为增加了部分极限场景，极限场景对取值范围具有代表性，仅需选取40～50 个常规场景，在计算结果上便可实现相似的效果，同时提高了求解效率。根据式（4）可以得出，场景数量越多，Wasserstein 球的半径越小，DRO 越趋向于确定性SO，故日前总成本随场景数量的增加而减小。

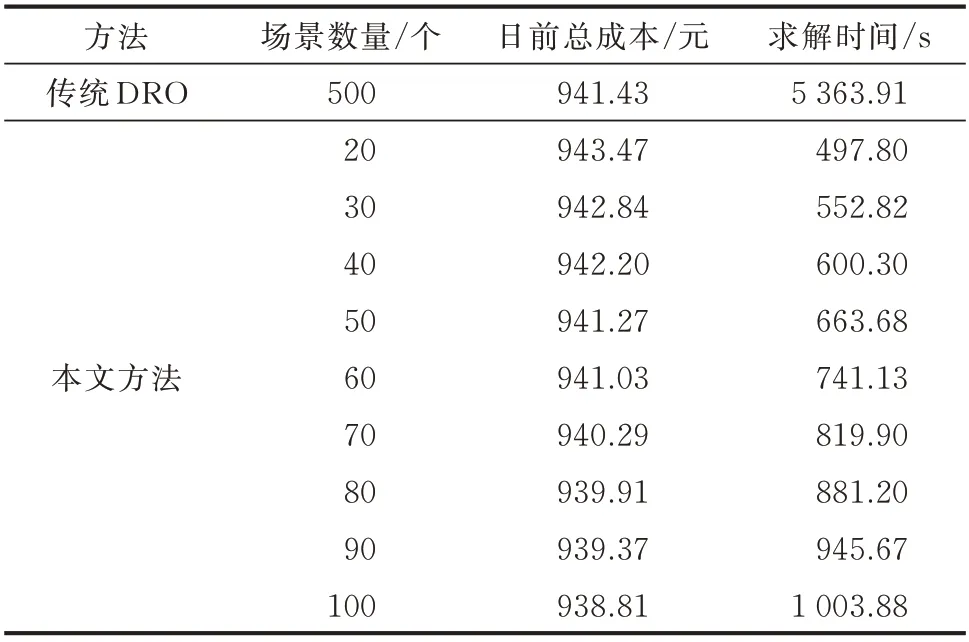
表3 相似效果下不同方法所需场景数量Table 3 Numbers of scenarios required by different methods with similar effects

3.4 置信度取值分析

为了体现式（4）中置信度β 的作用，本文选取不同的置信度取值分析其对结果的影响。当置信度取值为0.55、0.75 和0.95 时，日前总成本分别为934.63、938.18、941.27 元。由此可得，置信度越高，Wasserstein 球的半径越大，概率分布模糊集的范围越大，日前总成本越大；反之，置信度越低，DRO 越趋向于确定性SO，日前总成本越小。

4 结语

为了解决不确定环境下并网型微电网运行优化问题，本文提出了考虑极限场景的DRO 方法。考虑源荷不确定性构造概率分布模糊集，利用极限场景修正该模糊集，建立并网型微电网双层运行优化模型，采用改进ATC 进行联合优化求解，最后通过仿真验证。本文得到的结论如下：

1）由于极限场景可以包含随机变量的所有取值空间，具有一定的代表性，利用极限场景修正不确定集可以提升不确定集的鲁棒性，避免场景集过大，提高求解效率；

2）考虑到微电网与配电网属于不同的利益主体，建立微电网与配电网的双层运行优化模型可以充分考虑两者的利益诉求，使得各自的优化目标实现平衡；

3）仿真结果表明，与传统DRO 和传统RO 相比，本文所提方法在并网型微电网日前运行优化问题上表现优越，效果稳定。

本文仅对并网型单一微电网系统进行分析，下一步的工作将考虑该方法在多微电网系统中的适用性，进一步完善系统模型和优化方法。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。