基于分布鲁棒机会约束的充电运营商参与调峰市场投标策略

文艺林，胡泽春，宁 剑，刘礼恺

（1. 清华大学电机工程与应用电子技术系，北京市 100084；2. 国家电网有限公司华北分部，北京市 100053）

0 引言

近年来，全球电动汽车（electric vehicle，EV）的保有量持续大幅增长［1-2］。一方面，由于EV 的充电负荷属于大功率负载［3］，电力系统运行的安全稳定面临挑战［4］。另一方面，EV 的充电负荷具有灵活可调的能力，这使得它有潜力为电力系统提供调峰辅助服务，以促进间歇性新能源发电的消纳，提升电力系统运行的稳定性与经济效益［5-6］。

EV 充电运营商参与调峰辅助服务市场（以下简称“调峰市场”），需要在日前完成价格和负荷曲线等信息的申报，这些申报信息将用于市场的集中出清［7］。运营商在日前申报环节将考虑其所有EV 的调控能力，如何根据EV 的运行数据，定量地评估其调控能力，并为充电运营商的日前投标提供指导性的意见，是目前亟待研究的问题。

近几年国内外学者对EV 参与电网调控的研究中，主要是从电网运营商与充电运营商2 个角度进行考虑。站在电网运营商的角度，需设计对EV 的调度策略或市场机制，使得电网安全经济地运行。这类研究的优化目标一般是最小化电网负荷峰值［8］、峰谷差［9］、负荷方差［10-11］和发电成本［12］等。然而，站在电网运营商角度的研究一般对充电站运营商的建模不够细致，很少涉及调节能力不确定性的问题。

站在充电运营商的角度，可通过调节EV 的充电功率，尽可能在电价低或补贴力度更大的时期充电来最大化经济利益，目标函数一般是最小化运营商的充电成本或最大化利润。文献［13-15］考虑实时到达的订单需求，采用模型预测控制的方法求解每个充电桩的充电功率，然而这些文献中都没有考虑充电需求的不确定性。文献［16］考虑EV 离开时间的不确定性，通过离开时间的概率密度函数构造充电状态指示函数，据此调节充电功率，这种方法需要大量的历史数据且无法控制决策的风险与收益。文献［17］利用神经网络来预测调控能力，虽然神经网络的拟合能力可能比简单平均效果更好，但也缺乏调节能力不确定性的考量，无法控制风险与收益。

此外，不同类别的EV 作为可控负荷时有着不同的调控能力［18］，现有文献中往往没有对此进行详细的讨论，例如文献［13-15，19］将充电需求统一用起止时间和起止电量来描述，事实上这种数据结构只适用于单段充电需求。文献［20-21］则基于公交车发车时间表生成公交车的多段充电需求，在约束条件中考虑公交车多次充电以维持其全天运行。现有文献中对这2 种典型场景没有建立统一的模型，为运营商聚合不同类型充电站带来困难。

考虑到现有研究中的不足，本文首先将充电桩按照数据结构不同分为公共充电桩和专用充电桩两大类，提出了一种刻画充电桩调控能力的统一模型。由于充电桩的调控能力与EV 的出行规律强相关，而运行规律又难以用模型刻画，因此，本文使用数据驱动的分布鲁棒机会约束（distributionally robust chance constraint，DRCC）［22］来描述EV 调控能力的不确定性。进一步，将DRCC 描述的EV 调控能力用于充电运营商参与调峰市场的日前投标决策过程，提出了双层投标-分配优化模型。算例比较了不同类型充电站在多种优化方案下的经济效益与风险，分析了DRCC 调控能力模型和双层优化模型的优势，验证了本文所提方法的有效性。

1 EV 可调空间基本模型

EV 的可调空间是EV 参与电网调控的所有可能的充电负荷曲线集合。EV 的可调空间与EV 的出行规律有关，对于不同类型的充电桩，其表现形式不同：公共充电桩需要服务随机到达的充电订单，满足订单的充电需求；而公交桩、私人桩等专用充电桩往往仅服务固定的一辆或几辆EV。二者的区别在于，公共充电桩的充电需求只包含单段充电过程，必须在规定的时间范围内达到目标电量，而专用充电桩可以在EV 的多段停靠时间中充电，只要总体上能够维持EV 的运行即可。

本章分别考虑这两类充电站的特点，构建了一个统一的EV 可调空间模型。

1.1 公共充电桩的充电需求建模

本文主要讨论的是具有调控能力的公共充电桩，其多位于商业区或工业园区的停车场等目的地，在上班或休闲购物等期间，EV 可能长时间停靠在站内。这类公共充电桩所接收到的一个完整的充电需求包含到达时间ta、预期离开时间td、预期充电量ed以及最大电池容量emax等信息，充电过程需要在离开时间之前达到预期电量。如图1 所示，给定上述信息，则该订单对应的需求曲线Et定义为在td时刻幅值为ed的阶跃函数，而时刻ta到td之间均为充电功率的可调时间。

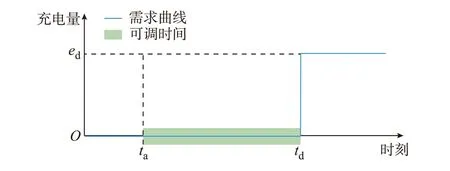
图1 公共充电桩单个充电需求的需求曲线与可调时间Fig.1 Demand curve and dispatchable time of a single charging demand for public charging pile

将时间离散化为若干个时间段，在可调时间的基础上定义最大可调功率Pmaxt，如式（1）所示，用于表征在第t 个时段EV 的最大充电功率。

式中：Pchg为EV 充电的额定功率；Γ 为可调时间段的集合。

1.2 专用充电桩的充电需求建模

专用充电桩包括公交桩、私人桩、公务车专用桩、环卫车专用桩等，其特点是它只为固定的一辆或多辆EV 服务，这使得充电运营商可以统计其电能需求规律。专用充电桩中不同细分类型的区别只在于时间尺度和随机性强弱的不同。

专用充电桩的充电过程可以有多段，需保证EV 运行时电池电量不耗尽，并且一般需要在优化的最后一个时段将电量恢复到初始水平，以保障随后的运行需求。根据EV 每一次出行的离开时间和所需电量信息都可以用类似图1 的方法构造一条“需求曲线”，将每段行程的“需求曲线”按时间段叠加，即可得到适用于专用充电桩的需求曲线。下面以公交专用桩和私人专用桩这两类典型的专用桩为例，详细说明专用充电桩的充电需求建模方法。

1.2.1 公交专用桩的充电需求建模

公交车每天按照排班表运行，一天中可能多次停靠在充电站内进行充电，每次出行的时间和剩余电量可以被记录下来，一次出行前后的剩余电量差即为公交车在外的耗电量。假设一辆公交车在td0时刻第1 次出行，ta1时刻返回站内，耗电量为ed1；td1时刻第2 次出行，ta2时刻返回站内，总耗电量达到ed2，根据上述原则构造的需求曲线与可调时间如图2 所示。

图2 单辆电动公交车的需求曲线与可调时间Fig.2 Demand curve and dispatchable time of a single electric bus

需要指出的是，在不可调的时间段内，充电桩无法也无须获取其真实的耗电量变化曲线，因为一个可行的充电过程会在可调时间内提前将电量充到高于用电需求的水平。因此，矩形ABCD 中从D 到B的任意一段曲线在优化模型中都是等价的，取DAB这一段折线是为了保持与公共充电桩需求曲线的一致性。

1.2.2 私人专用桩的充电需求建模

私人EV 的出行时间和剩余电量信息同样可以被记录下来，所以可以用类似公交车的方式，根据每段出行前后的剩余电量差来构造需求曲线。电动私家车的出行频率远低于公交车，大多数情况下多天才充电一次。如果优化的时间窗取得足够长，私人桩的需求曲线也应该为多段阶跃函数叠加，但由于优化模型计算的时间尺度一般不超过一天，因此私人专用桩的需求曲线一般是阶跃函数。此外，由于私家车可能在外充电，其出行前后的剩余电量差可能并非真实耗电量，甚至可能为负，这并不影响需求曲线的构造。根据私家车的离开时间、返回时间与剩余电量差等数据，生成的需求曲线与可调时间如图3 所示。

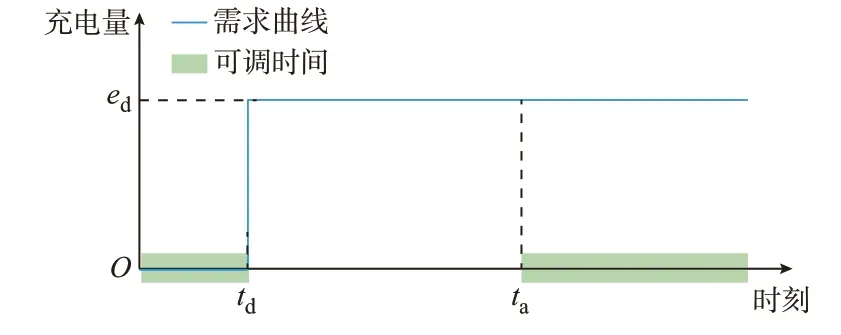
图3 单辆电动私家车的需求曲线与可调时间Fig.3 Demand curve and dispatchable time of a single private EV

1.3 EV 可调空间统一模型

虽然公共充电桩和专用充电桩的数据结构不同，但根据不同的数据都可以生成需求曲线，并且可通过式（1）计算每个时段的最大可调功率。因此，不同类型充电桩的可调空间数学模型可以具有统一的形式。若给定需求曲线Et与最大可调功率Pmaxt，则一辆EV 的可调空间约束集如下：式中：Pt为决策变量，表示EV 在t 时段的实际充电功率；e0对于公共充电桩的充电需求是其预期达到的电池电量，对于专用桩是时间窗的初始电量；-e 和-e 分别为电池电量的上、下界；T 为总时间段数；ΔT为每个时间段的长度。约束（2）表示EV 的可调功率边界约束；约束（3）表示任何时段（包括可调时间与不可调时间）的电池电量需在电池容量限度内；约束（4）表示在优化的最后一个时段需要达到目标电量（公共充电桩）或将电量恢复到初始水平（专用充电桩）。

2 基于分布鲁棒机会约束的EV 可调空间模型

在充电运营商的日前投标过程中，虽然可调空间模型中的参数不可观测，但其历史数据样本却可以方便地获取。虽然EV 的运行具有随机性，但也呈现出一定的规律，当数据量增大时，规律性得以体现。充电运营商可以利用充电需求的规律性预测次日的EV 可调空间，进而计算出参与调峰市场的总体充电曲线，计算结果的可靠程度不仅取决于随机性的大小，还取决于使用历史数据的方式。

要预测次日的EV 可调空间，一种简便的做法是对历史上若干天的可调空间模型中的各个参数取平均，则可以沿用约束（2）至约束（4）进行决策，这种做法在本文中被称为“ 抽样平均”（sample average，SA）。SA 的缺陷是：通过历史样本均值确定的可调空间只是对真实可调空间的粗略估计，据此计算出的充电功率曲线很可能不满足实际充电需求，从而在实时运行时带来额外的成本。

描述随机变量的经典方法还有场景集优化（scenario-based optimization，SO）和鲁棒优化（robust optimization，RO）。SO 是指通过统计、聚类和场景削减等手段由历史数据样本生成场景集，令充电功率在每个场景下都满足约束（2）至约束（4）。相对于SA 而言，SO 所确定的决策空间更加保守，更有可能满足真实的可调空间，但SO 的难点在于典型场景难以确定。RO 是指先给出随机变量所在的集合，计算不确定集合中最坏情况下的最优解。决定RO 性能的关键是不确定集合的准确性，一般采用的集合形式包括盒式集、多面体、椭球集等。在本文的问题中，随机变量与EV 的出行规律相关，不确定集难以确定，如果直接采用RO，则模型会过于保守。

因此，本文采用数据驱动的DRCC 对可调空间进行建模，这种方法能够在有限的历史数据样本上充分挖掘随机变量的分布信息，还可以通过调节参数控制保守程度，适合用作充电运营商的投标决策。

2.1 EV 可调空间机会约束

括号内不等式左侧的表达式是关于ξ 线性的，系数向量ak和标量bk与决策变量x 有关（事实上本问题中ak也是常数向量，为不失一般性，可以写成上述形式）。

2.2 基于Wasserstein 距离的分布鲁棒机会约束

由于随机变量ξ 的分布未知，机会约束（5）至约束（8）无法直接用于计算。在这种情况下，可以结合历史数据将原机会约束转化为DRCC。分布鲁棒的基本思想是在与样本分布临近的那些分布中找出最坏情况。构造分布集合的方法有很多，现有文献中一种较为普遍的做法是基于一、二阶矩构造盒式模糊集［23-24］，这种方法的局限性在于矩对随机样本特征的刻画是不全面的。Wasserstein 距离作为用于刻画2 个概率分布之间距离的方法，近几年被广泛地用于分布鲁棒的算法研究［25］，本文也基于Wasserstein 距离构建DRCC，具体步骤如下。

首先，如式（10）所示，机会约束（9）可以近似地转化为条件风险价值（conditional value at risk，CVaR）约束。这一转化的好处是使得后续的问题可以线性化，易于求解。然而这一转化并非等价转化，会使得原来的机会约束更加保守。尽管如此，由于保守程度并不大，在工程上一般能够接受，因此在研究中被广泛使用［26-27］。

基于Wasserstein 距离的DRCC 需要先粗略地设定随机变量ξ 所在的集合，这对后续结果影响不大，一般取多面集Ξ={ξ|Cξ ≤d }。取范数为l1范数（对偶范数为l∞范数）时，CVaR 约束（10）可以等价转化为以下形式的DRCC［22，25］：

附录A 给出了约束（12）至约束（15）的具体表达式，其实际上是一组线性约束，可以很容易地嵌入一些优化模型中，并且不改变问题的凸性。

3 充电服务运营商参与调峰市场的双层投标-分配模型

将DRCC 描述的EV 可调空间用于EV 充电运营商参与调峰市场的日前决策过程中，该决策过程可分为2 层。上层优化模型是运营商根据所有充电站的可调空间计算总体最优功率曲线，下层优化模型是将确定的总功率曲线分配至每个充电站。

需要指出的是，运营商应使用不同的参数ε 多次计算上层问题，确定最优的总功率方案后，再计算下层问题。在上层优化问题中，为了使运营商能够权衡收益与违约风险，需要使用DRCC 描述的可调空间。而在下层问题中，只须使用SA 模型来描述各个充电站的可调空间，这是因为在运营商整体满足调节能力约束的前提下，单个充电站不满足约束的功率可以在其他充电站得到补充。

3.1 上层优化模型——总功率投标决策模型

综上所述，充电服务运营商参与调峰市场的日前决策模型目标函数为式（16），约束条件包括式（12）至式（15）、式（17）和式（19），该模型是混合整数线性优化模型。

3.2 下层优化模型——功率分配模型

当运营商的总功率曲线确定之后，运营商可以为每个充电站分配合适的功率曲线，即以最小化分配的误差为目标，满足每个充电站的SA 可调空间约束，优化问题如下：

上述双层优化机制使得运营商对外表现出风险管理的保守性，而内部资源的能量管理却具有灵活性。事实上运营商还有一种更为稳健的决策方案，即对每个充电站使用DRCC 可调空间计算出最优功率曲线，再叠加得到运营商的总投标功率曲线。但这种方法会使得决策过于保守，不能利用大量EV 随机性互补的优势，并且由于可调参数过多，难以控制运营商总体的保守程度。算例将对这2 种方案进行对比。

4 算例仿真

4.1 不同类型充电站参与调峰市场的效果分析

对单个充电站的分析能够揭示出不同类型充电站的特点。本节对公共充电站、公交充电站以及私人充电桩集群这几类典型的充电站参与调峰市场的表现进行了仿真分析。取前10 d 的充电功率曲线平均值作为基准负荷，利用蒙特卡洛模拟生成各类EV 的充电需求信息。模拟使用的参数是根据京津唐电网范围内的各类EV 充电负荷实际数据，结合各类EV 出行规律合理设置的，具体参数见附录B。假设公共充电站与私人桩服务的EV 电池最大容量为40 kW，额定充电功率为7 kW，电动公交车电池容量为240 kW，额定充电功率为60 kW。

仿真测试中，SA、SO、RO 和DRCC 模型的平均求解时间分别为0.120 6、0.175 8、0.140 6、3.283 8 s。需要强调的是，本文模型考虑的是EV 聚合后的随机变量，求解时间不会随EV 数量的增加而变化。虽然DRCC 模型的求解时间高于其他3 个模型，但由于本文所提方法主要用于运营商的日前投标决策，所以DRCC 秒级的计算时间同样可以适用于实际应用需求。

4.1.1 不同类型充电站的最优充电过程对比

将DRCC 中参数ε 设为0.4，3 类充电站在不同优化模型下的日前最优功率曲线如图5 所示。其中RO 在公共充电站和私人桩集群的算例下均不可行，因此在图5（a）和（c）中无相关功率曲线。对比图4 可以看出，在夜间调峰价格较高的时期，即01：00—05：00，3 类充电站的基准功率曲线都大致处于低谷，上调空间非常大。几种模型计算得到的充电功率曲线不同程度地利用了这一上调空间，但也有细微的差别：由于SA 是选取历史数据的平均值作为功率上界，所以负荷曲线峰值超出了某些样本最大功率；SO 得到的功率曲线紧贴历史数据的边界，没有越界；DRCC 不仅没有越界，还留出了一定的裕度；RO 需要留出的裕度最大，在公交车充电站算例中的负荷峰值远低于其他3 个模型，且在公共充电站和私人桩集群的算例中致使模型无可行解。

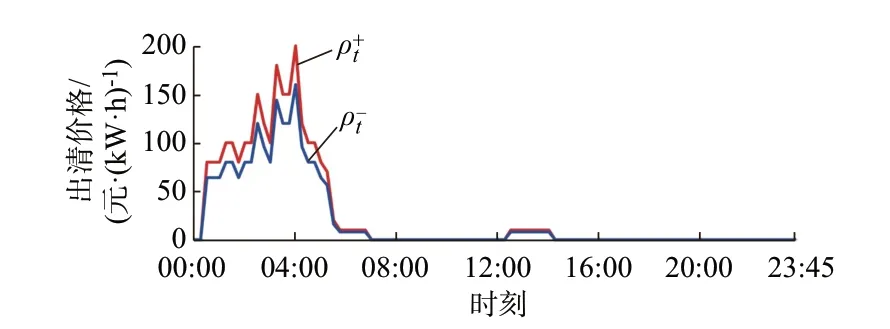
图4 调峰市场出清价格Fig.4 Clearing price of peak regulation market

对比图5（a）至（c）可以看出，由于公共充电站比公交和私家车运行的随机性更强，随机变量历史样本的波动更大，因此公共充电站的DRCC 模型在相同参数下更加保守（留出的裕度更大）。

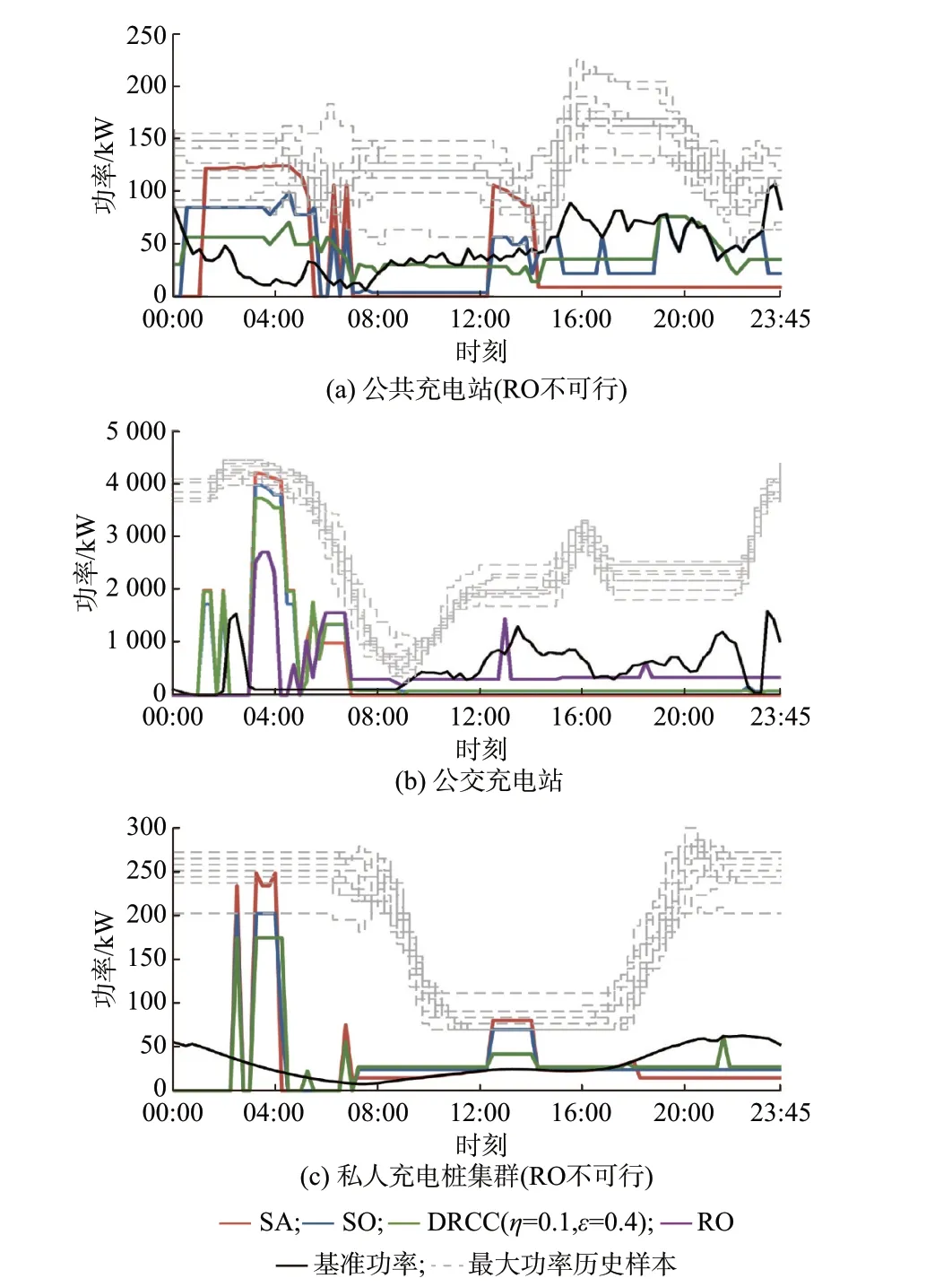
图5 3 种充电站在不同优化模型下的日前最优功率Fig.5 Day-ahead optimal power of three types of charging stations in different optimization models

除功率曲线以外，能量的变化趋势同样是本文模型中考虑的因素。以公交充电站为例，不同计算方法得到的能量变化曲线如附录C 图C1 所示。由于EV 的停留时间较长，能量边界的约束较为宽松，大多数时候边界并没有起作用。但在最后一刻，SA恰好恢复到了初始的能量水平，SO 留出了一定的裕量（其实是样本中最大的初始能量），DRCC 留出的裕度比SO 略大，RO 留出的裕度最大。

通过在DRCC 模型中设定不同的ε 值，计算得到的功率曲线如附录C 图C2 所示。当ε 很小时，由于Wasserstein 球中的分布趋近于在样本空间上的离散均匀分布，所以功率曲线的结果与SO 几乎相同。随着ε 的增加，功率曲线在峰值处留出的裕度也会加大，意味着决策越保守。在随后的4.1.2 节中，将进一步讨论参数ε 对优化效果的影响。

4.1.2 不同类型充电站的经济效益与风险对比

4.1.1 节分析了3 类充电站在不同计算方法下最优充电过程的特点，这些特点会影响到充电站参与调峰市场的收益与风险。本节对SA、SO、RO、DRCC 这4 种模型以及DRCC 不同参数决策后的经济效益与风险进行了统计分析。经济效益是指充电站在参与调峰市场后的运行成本减少值。风险是指日前申报的功率曲线在日内无法执行的可能性，例如功率超出上界或充电电量未达到需求值等情况。当出现这些情况时，充电运营商需要承担违约赔偿、绩效评分降低或在实时市场中购买其他主体提供的调节容量等额外成本。

通过随机模拟新的10 d 的可调空间数据（以下称为“测试集”），可以统计日前功率曲线在测试集上Pv作为量度风险的指标。根据实际的市场规则以及具体违背的约束类型，该风险造成的损失可以量化。本文考虑以下2 种损失。

1）根据华北电网的负荷调峰市场运行规则，当日前申报的功率曲线在日内无法达到时，若实际功率与投标功率差距在一定范围内，可按实际功率结算，若差距超出该范围，则该时段收益为0。本文中设置该最大偏差率为10%。

2）若日前优化结果中的总充电电量未达到日内实际需求值，为补齐不足部分，需要在实时市场上额外购电。本文设置在实时市场上的购电电价为日前能量市场的1.2 倍。

综合考虑调峰市场的收益与以上2 种损失，则容易计算出日前功率曲线在测试集上的平均实际运行成本（ARC）。3 类充电站在不同优化模型下的目标函数值、违约率Pv和ARC 如表1 所示。

表1 3 种充电站在不同优化模型下的经济效益与风险对比Table 1 Comparison of economic benefits and risks of three kinds of charging stations in different optimization models

在3 种充电站的算例中，SA 得到的目标函数值最低，但违背约束的概率Pv最高，ARC 也最高。SO的Pv相对SA 显著降低，但目标函数值也明显提高，综合指标ARC 有所降低。虽然RO 在公交充电站算例中的Pv为0，但ARC 远高于DRCC，并且在公共充电站和私人充电桩集群的算例中都导致模型无解。DRCC 在参数ε 很小时结果与SO 十分接近，随着ε 的增加，DRCC 可使得Pv进一步减小，但目标函数值会相应地增加，ARC 呈现先减小后增加或一直增加的规律。这是因为当ε 较小时，由于决策不够保守，运营商在日内付出的额外成本较高；而当ε 较大时，决策过分保守，则参与调峰市场的收益变少。

在DRCC 模型中，当ε=1 时，公共充电站的算例已经没有可行解。结合附录C 图C2 可以推测，这是由于公共充电站的历史数据波动性太大，导致ε=1 时模型的保守度过大，以致于可行域变为空集。当ε 足够大时，公交充电站在测试集上违背约束的概率可以减小到0，而公共充电站无法达到0，这是由于充电需求随机性太强导致的。由此可见，充电需求随机性较小的充电站在参与调峰市场时拥有相对更大的决策空间，具有灵活的调节风险的能力。

充电运营商可以通过调整参数ε 得到使得ARC最小的功率曲线，作为日前投标方案，这一调整过程可以通过一些经典的单变量无约束优化算法（例如二分法、黄金分割法等）实现。在此基础上，可由式（24）定义最大成本削减率（MCRR）指标rMCRR，用于评估充电站参与调峰市场的效率。

式中：Amin为参与调峰服务的ARC 最小值；A0为未参与调峰服务的运行成本。

表2 列出了上述3 种充电站的最大成本削减率，可见公交充电站的最大成本削减率最高，私人充电桩集群次之，公共充电站最低。这说明专用充电站参与调峰市场的效益比公共充电站更高，验证了第1 章中对不同类型充电站调节能力的论断。私人充电桩集群的最大成本削减率比公交充电站低，是因为电动私家车的电量需求少，且存在无法在夜间充电的情况，夜间的调峰时段不能被充分利用。

表2 不同类型充电站的最大成本削减率Table 2 The maximum cost reduction rates of different charging stations

4.2 充电运营商参与调峰市场的投标结果分析

本节使用所提的双层投标-分配决策模型，计算一个拥有多个充电站的运营商的日前投标策略。该运营商拥有的资源包括1 个公交充电站、1 个大型公共充电站、2 个小型公共充电站以及2 个私人充电桩集群，其中充电需求数据或出行数据均由蒙特卡洛模拟生成，模拟使用的参数是根据京津唐电网范围内的各类EV 充电负荷实际数据，结合各类EV 出行规律合理设置的，具体参数见附录D。

附录E 图E1 给出了双层优化模型所得到的总功率曲线和各个充电站的功率曲线。可见，模型成功将功率分配到了每个站内，根据不同充电站体量大小不同，分配的功率比例也有所不同。作为对比，本文还对每个充电站独立使用DRCC 可调空间进行计算，其总功率的结果与双层优化方法的对比如图E2 所示。可以看出，独立决策模型的功率曲线夜间峰值更低，说明其结果会更加保守。

运营商内每个充电站的功率曲线如附录E 图E3 所示。2 个体量较大的充电站——公交充电站和大型公共充电站的负荷曲线趋势与总功率曲线一致，但私人充电桩集群和小型公共充电站的趋势却不同，尤其是2 个私人充电桩集群，独立决策的负荷夜间峰值反而更高。这是因为第2 阶段的分配模型是多解的，只须在能够匹配总功率的方案中选择一个即可。2 个体量较大的充电站功率峰值已经足够高，且求解器在体量较小的充电站之间倾向于选择较为“平均”的解，才导致了这一结果。这并不代表私人充电桩集群或小型公共充电站夜间峰值功率还有上调空间，因为如果仅仅这些功率峰值增加，则总功率峰值也会增加，导致总体DRCC 约束无法满足。

表3 进一步对比了这2 种投标策略的目标函数值与违背约束的概率。其中，双层优化在目标函数值为9 280.0 元时，Pv达到0；而独立决策方案虽然每一个充电站的Pv都无法降至0，但总体的Pv却能达到0，此时总体目标函数值为9 520.6 元，比双层优化方法的目标函数更高。此外，要控制独立决策的保守程度，需要调整每个充电站的ε 参数，而双层优化模型的保守程度仅需通过一个参数就可得到控制，在需要权衡风险与收益的实际应用场景中效率更高。

表3 2 种投标策略的目标函数值与违约概率对比Table 3 Comparison of objective function values and default probability of two bidding strategies

5 结语

本文首先分析了不同类型EV 的运行特征，构建了EV 参与调峰市场的统一可调空间模型。其次，考虑到EV 调节能力的不确定性，将可调空间模型表示为DRCC。进一步，将该约束集嵌入充电运营商参与调峰市场的优化问题中，设计了一个双层投标-分配决策模型，计算出充电运营商的最优申报功率曲线和各充电站的参考功率曲线。

仿真结果显示，DRCC 相比SO 保留了鲁棒性，相比RO 降低了保守性，并且保守程度可以调节。通过不同类型充电站收益指标的对比，说明充电需求的随机性越强，参与调峰市场的效率越低。公交充电站的充电需求随机性最弱，因此效益最高。所提出的运营商双层投标-分配策略中，在上层优化问题中使用DRCC 可调空间使得运营商能够进行风险权衡，而在下层问题中使用的SA 可调空间使得运营商可以灵活地调度内部资源。相比每个充电站独立使用DRCC 进行决策，双层投标-分配策略更加简洁且更具实用性。

本文所提的方法可以被运营商用于以下几个方面的决策：

1）运营商在最初规划接入的充电站时，就可以使用本文的模型评估每个充电站最大效益，尽量选择效益较大的充电站接入。

2）在日前投标阶段，运营商可以应用本文所提的投标决策模型中的上层模型，通过调整参数的值找到平均实际运行成本最低的投标方案。

3）当投标方案确定后，运营商可以使用下层模型制定每个充电站的参考功率曲线，为实时运行提供指导。

理论上，随机变量的样本越多，DRCC 对分布的拟合就越精准。但实际上，充电站或EV 的运行条件随时间变化，过早的历史数据可能反而使得模型过拟合，偏离当前的真实状态。此外，EV 的运行还可能在工作日与节假日呈现不同的规律性。EV 充电运营商在应用本文模型时需考虑这些因素，选择合理的样本数据集。例如，在工作日选择最近10 个工作日的充电需求数据，在周末选择最近10 个周末的充电需求数据。

本文的模型中没有考虑机会约束在时间上的相关性，以及调峰市场出清电价的不确定性，今后的研究将着眼于这些因素的建模。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。