含可再生能源电力系统可靠性评估的非参数重要性分层抽样法

蔡霁霖，郝丽丽，张柯琪

（1. 南京工业大学电气工程与控制科学学院，江苏省 南京市 211816；2. 国网常州供电公司，江苏省 常州市 210024）

0 引言

随着新能源发电渗透率增加，传统发电厂年平均利用小时数逐年下降，但弃风、弃光、弃水现象仍时有发生，引发了电力系统中发电资源是否冗余的讨论［1-2］。因此，作为发电充裕度量化手段的电力系统可靠性评估得到关注。

早期的电力系统可靠性评估主要依赖解析法，其计算复杂度取决于电力系统解空间的复杂度［3］。为了缓解状态空间过大给解析法带来的效率下降问题，文献［4］提出一种基于影响增量和高阶故障状态削减的可靠性评估解耦方法。文献［5］则提出一种基于卷积法和传输点输电能力-负荷解耦模型的可靠性评估方法。然而，随着大量可再生能源并网，系统内随机变量大幅增加，其相关性结构也愈发复杂［6-7］，传统解析法的瓶颈无法彻底解决。因此，基于蒙特卡洛采样（Monte Carlo sampling，MCS）思想的可靠性评估模拟法受到了关注［8-11］。

虽然理论上只要样本容量足够大，MCS 法得到的可靠性指标将无限逼近真实值，但对大规模高可靠性电力系统进行可靠性评估时，对每一个样本都运行一次计及网络安全约束和随机变量相关性的最优潮流算法的代价较高。因此，需尽可能缩减MCS法的样本容量。为此，许多研究将MCS 法与各类方差削减方法结合起来，其中效果最为突出的是重要性采样（importance sampling，IS）法［12-14］。文献［15］利用IS 法修正前后停运率差异大的元件，构成重要状态空间来提升采样效率。文献［16］将元件状态空间分为低阶和高阶子空间，并采用IS 法计算高阶空间可靠性指标。文献［17］通过在IS 法修正后的系统状态函数中增加额外控制项，进一步减小IS 法估计可靠性指标时的方差。为同时处理连续和离散变量，文献［18］提出一种基于交叉熵思想的IS 法，求取各类随机变量的重要性分布来替代各自的原始分布，提高故障样本的出现概率。文献［19］在文献［18］的基础上，针对系统中同一节点常接有多台参数型号相同机组的情况，利用多项分布实现随机变量降维。

然而，IS 法对于偏移后的分布函数仍采用简单随机采样获取样本，因此依旧存在样本重复度高的可能，故无法保证用少量随机样本表征概率分布全貌的效果。实际上，提高样本对概率分布的表征能力同样能降低估计量方差，而分层抽样法就是按照这一思路构建的一类方法［20］，如拉丁超立方采样（Latin hypercube sampling，LHS）法［21-23］。

从理论上来说，IS 法改变概率分布，不改变样本抽取方法，LHS 法恰好与之相反，故将IS 法与LHS 法结合，应该能提升指标计算效率。文献［24］对此进行了尝试，但只考虑了离散变量，未涉及LHS 法在连续变量相关性控制时如何与IS 法配合。事实上，LHS 法与IS 法结合存在以下问题：LHS 法在对样本进行相关性控制时，需使用相关系数矩阵；而IS 法则需要预先指定偏移分布的带参数函数形式［25］，但只有少量函数形式能够方便地提取出相关系数矩阵，可这些函数形式不一定能完全表征各类随机变量的复杂边际分布和相关性结构特征。

针对上述问题，本文提出了一种非参数重要性分层抽样法，该方法主要由IS 法中偏移分布的非参数构建方法和LHS 法相关性控制部分与IS 法偏移分布兼容的实现方法2 个部分组成。将该方法应用于含多新能源厂站的电力系统可靠性评估，并利用实际新能源厂站的历史出力数据和IEEE RTS-79测试系统设计了算例，验证了该方法的有效性。

1 小概率事件分析中的IS 和LHS

1.1 小概率事件分析的数学模型

在小概率事件分析中，最受关注的是对事件发生的概率进行估计。本文关注的电力系统可靠性评估中，离散变量（发电机组、线路运行状态等）与连续变量（负荷、风电出力等）相互独立，在此前提下事件发生概率的数学表达式如下。

式中：S(x)为系统状态评价函数；Sth为人为设定的阈值；γ 表示S（x）小于Sth的概率；E(·)表示求期望值；I(·)表示一个指示函数，括号内表达式成立时取1，反之取0；x 为系统内所有随机变量组成的向量，简称系统状态向量；xdv为所有离散变量组成的向量；xcv为所有连续变量组成的向量，三者间的关系为x=[ xdv，xcv]；Ωdv和Ωcv分别为xdv和xcv的取值空间；p(xdv)和f (xcv)分别为离散变量和连续变量的概率密度函数（probability density function，PDF）。

要估计式（1）中γ 的值，一个最直接的方法就是采用MCS 法，由此构建出的估计量如下。

式中：βMCS为γMCS的方差系数；var(·)表示求方差。

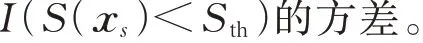
1.2 基于交叉熵思想的IS 法

IS 法的基本思想是对式（1）做如下等价变换：

由式（4）可知，IS 法本质上是一个两阶段过程：第1 阶段对应式（4）前2 行，是对随机向量的概率分布进行修正并得到IS-PDF；第2 阶段对应式（4）第3 行，用MCS 法修正分布采样，并估计关心的指标数值。

文献［18］指出，IS 法理论上最优的IS-PDF 是无法得到的，故许多学者提出了逼近最优分布的方法［26-27］。其中，基于交叉熵思想的修正方法是最为广泛使用的方法之一［28-29］，其基本思想是预先为h(xdv)和g(xcv)选取含待定参数的函数形式，将待定参数作为优化变量，以该函数形式与理论最优分布的交叉熵最小为目标函数，构建并求解优化模型，从而得到待定参数最优值，并据此确定h(xdv)和g(xcv)的表达式［18］。

1.3 LHS 法

LHS 法也分为2 个阶段：独立分层采样和相关性控制［23］。第1 阶段进行独立分层采样时，暂不考虑随机向量x 中各变量间的相关性，只用各变量的边际分布进行采样。记x 中的变量个数为K，所需样本容量为N。则第1 阶段结束时将会得到一个各行之间没有相关性的样本矩阵X。在第2 阶段的相关性控制过程中，利用连续变量间相关系数矩阵，在X 中加入指定的相关性，具体步骤可参见文献［23］。

2 非参数重要性分层抽样法的算法原理设计

传统IS 法的重点在于找到一个效果较好的IS-PDF，将样本集中到对指标贡献更大的“重要性区域”，而在该区域内的采样仍然采用简单随机采样，存在出现大量重复或相似样本的可能性，故其加速计算的潜力仍有挖掘空间。因此，本文将IS 法与LHS 法结合，提出一种非参数重要性分层抽样（nonparametric stratified importance sampling，NSIS）法来进一步挖掘IS 法的潜力。

2.1 NSIS 法设计思路

1）采用混合高斯模型（GMM）这一非参数化模型作为IS-PDF，GMM 的表达式如下［25］。

2）设计一种与GMM 兼容的改进LHS 方法，选择GMM 的理由如下。

①从保证IS 法性能不受损失的角度：理论最优IS-PDF 一般是一个非常规分布，例如存在多个不相连的、偏度不为0 的尖峰。如果预先选择一个确定性带参函数，则其在空间的基本形状是确定的。以正态分布密度函数为例，其有且只有一个尖峰，调节其参数都只能改变尖峰的位置和宽度，而无法改变尖峰的个数和偏度。因此，选择确定性带参函数从理论上就失去了无限逼近最优IS-PDF 的可能性。而GMM 作为一个非参数模型，只要给予足够分量，理论上能拟合各种边际分布和相关性结构，故其存在无限逼近最优IS-PDF 的可能。

②从与LHS 法结合的难易度角度：如1.3 节所述，LHS 法需要进行相关性控制，且控制过程中，变量间相关系数矩阵是一个重要参数，但大多数确定性带参的高维分布函数无法显式地提取相关系数矩阵。而GMM 的每个分量都显式包含相关系数矩阵。因此，相较其他分布，选择GMM 为IS-PDF 的基本形式，更容易让IS 法与LHS 法结合。

然而，即便GMM 拥有以上优点，其与LHS 法的结合仍不是无缝衔接。这是由于GMM 的每个分量都包含一个相关系数矩阵，而LHS 法进行相关性控制时，只需要一个相关系数矩阵。因此，两者的结合还需经过特定的设计才能达成，这也是本文所提NSIS 法的算法核心所在。

2.2 NSIS 法流程

NSIS 法也按照IS 法惯例分为2 个阶段，其一般性算法流程如下。其中，步骤3 中利用LHS 法采样GMM 的过程是NSIS 法的核心步骤，实现了IS 法与LHS 法的结合。

步骤1：开始NSIS 法的第1 阶段。记小概率事件中，xcv包含的变量个数为Kcv。以连续变量历史数据为原始样本，利用赤池信息准则和最大期望（EM）算法［25］，估计GMM 分量个数nGM以及各分量参数，即ωk、μk和Σk。

步骤2：从每个Σk中分离出标准差参数向量σk和线性相关系数矩阵ρk，即

先用LHS 法对所有离散变量xdv采样Nfir次，得到样本矩阵Xdv，共Nfir列，每列即为xdv的一个样本，其行数即为离散变量个数。

再用LHS 法对GMM 采样Nfir次，具体方法如下。

1）按照GMM 各分量的权重分配每个分量采样的样本数，即第k(k=1，2，…，nGM)个分量需采样ωkNfir次。初始化k=1。

2）对于第k 个分量，利用μk和σk中包含的信息，构建Kcv个连续变量的边际IS-PDF（均为一维正态分布函数），即

式中：Xk，e为第e 个变量利用GMM 第k 个分量采样出的ωkNfir个样本组成的向量；P 为一个行向量，由连续正整数序列{1，2，…，ωkNfir}打乱顺序所得；ε 为与P 维数相同的随机数向量，其每个元素都服从区间（0，1）上的均匀分布且互相独立；Φ-1k，e(·)表示φk，e(·)对应的累积分布函数的反函数。

Kcv个变量全部采样完毕后，将Xk，e（e=1，2，…，Kcv）组合成样本矩阵Xk，即

步骤4：根据交叉熵IS 法思想，采用所得样本更新IS-PDF 参数集{ωk，μk，Σk|k=1，2，…，nGM}。更新公式将在第3 章电力系统可靠性评估的具体应用场景下与其他离散变量的参数更新公式一并给出。

步骤5：判断样本矩阵X 中故障样本占比是否满足要求，若是，转步骤6，否则转步骤2。

步骤6：进入NSIS 法的第2 阶段。将第2 阶段采样样本总数记为Nsec。同样按照式（7）—式（10）所述方法对当前IS-PDF 分层采样Nsec个样本，并采用该样本按式（4）最后一行估计待求指标并输出。

3 NSIS 法在含可再生能源电力系统可靠性评估中的应用

在含可再生能源的电力系统中，系统状态x=[ xdv，xcv]可实例化为：

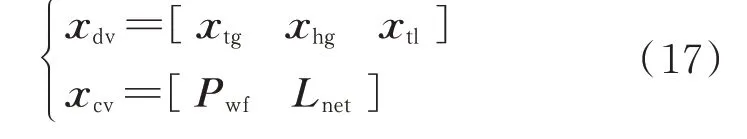
式中：xtg为系统中各火电机组状态组成的向量；xhg为系统中各水电机组状态组成的向量；xtl为系统中各输电线路状态组成的向量；Pwf为系统中各风电场最大可用功率组成的向量；Lnet为系统各负荷节点的净负荷组成的向量，净负荷的具体含义将在介绍Lnet的概率分布模型时给出。

式（1）在系统缺电概率（loss of load probability，LOLP）指标计算这一场合下实例化为：

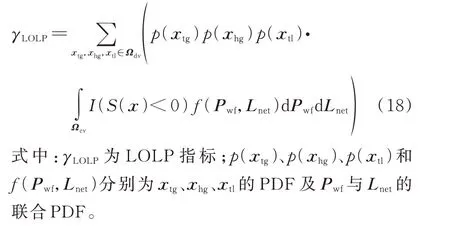
3.1 含可再生能源电力系统可靠性评估基本模型

在计算可靠性指标之前，需要明确式（18）中各函数的具体表达式，包括x 中各分量的原始PDF 和电力系统状态评价函数S（x）。

3.1.1 电力系统变量的原始PDF 模型

下面针对xtg、xhg、xtl的PDF 以及Pwf与Lnet的联合PDF 分别说明。

1）火电机组状态变量的PDF

xtg包含多个元素，可表示为：

由于水电机组任意时刻的最大可能出力受全年不同时期来水量和水头影响，因此需采用多状态模型建模。xhg，j的不同取值代表水电机组的最大可能出力处于不同水平，各状态具体数值可通过对水电机组的历史实际出力数据进行K-means 聚类得到。

式中：Lb为第b 个节点的负荷需求；Ppv，b为第b 个节点所接光伏电站的出力。

根据第b 个节点的光伏出力和负荷的历史数据，利用式（26）得到Lnet，b的历史数据。在构建联合PDF 时，将Lnet，b视作随机变量，而不再单独考虑Lb和Ppv，b。

对光伏采用净负荷处理方式的理由为：与风电不同，光伏与负荷的功率随时间的变化均具有较为固定的模式，如光伏夜间出力为0，晴天时最大出力出现在12：00—14：00 之间，而夜间负荷也处于低谷期，峰荷则一般出现在傍晚。为了保留形状相对固定的负荷和光伏出力日内曲线在时间上的对应关系，本文选择文献［30］中的净负荷法。在此基础上采用Copula 思想建立各风电场出力与各节点净负荷的联合PDF。本文采用文献［6］中提出的R-vine Copula 函数法拟合相关性结构，采用文献［31］中介绍的GMM 法拟合各变量的边际分布。由此得到联合PDF 表达式如下。

式中：crv(·)表示R-vine Copula 密度函数；F(Pwf)和F(Lnet)分别为Pwf和Lnet的累积分布函数；f (Lnet，b)表示第b 个节点的净负荷的原始边际PDF；f (Pwf，w)表示第w 座风电场出力的原始边际PDF。R-vine Copula 密度函数和GMM 的参数估计方法可分别参考文献［6］和文献［31］，此处不再重复说明。

3.1.2 电力系统状态评价函数定义

S（x）的定义需依托最小切负荷模型的目标函数值，其约束条件包括潮流约束、节点电压约束、输电线路传输功率约束等。

在电力系统规划和可靠性分析中，常采用基于直流潮流的最小切负荷模型，其数学表达式已在多篇文献中给出［18-19，25］，此处不再赘述，只给出该模型的目标函数，其表达式为：

式中：Gi为第i 台火电机组的装机容量。

需要说明的是，在NSIS 法第2 阶段正式估计可靠性指标时，Sth=0。但在第1 阶段求IS-PDF 参数时，Sth会动态调整，以加快参数寻优的速度，调整方式将在下节介绍。

3.2 基于NSIS 法的电力系统可靠性评估

3.2.1 NSIS 法计算电力系统可靠性指标过程

1）选取IS-PDF 的函数形式

对于离散变量xtg、xhg和xtl，其IS-PDF 选取与原分布相同的函数形式，即

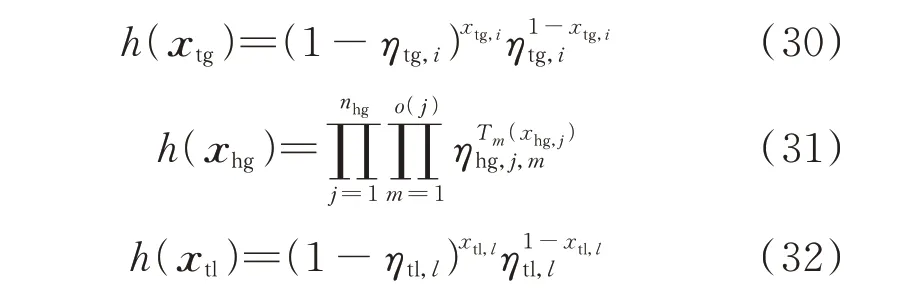
式中：ηtg，i、ηhg，j，m（m=1，2，…，o( j)）和ηtl，l分别为第i台火电机组、第j 台水电机组和第l 条输电线路需要优化的参数。

对于连续变量Pwf和Lnet，按照式（6）选择GMM作为联合IS-PDF 的基本函数形式，即

2）优化IS-PDF 参数

在确定各变量的基本函数形式后，即可对ISPDF 中的相关参数进行优化。为了提高参数优化效率，可以引入迭代过程，在迭代中动态调整Sth值进行参数的逐步更新，其具体步骤如下：

步骤1：按式（7）—式（16）所述方法对当前ISPDF 采样Nfir次。初次迭代时，采用原始PDF 进行采样。

步骤2：对每个样本计算其S（x）数值，从小到大排序得到序列{S(1)，S(2)，…，S(Nfir)}，提取排在第αNfir位的数值S(αNfir)，其中α 为处于缺电状态的样本比例。

步骤3：如果S(αNfir)≤0，说明以当前IS-PDF采样得到的样本中，能使系统处于缺电状态的样本比例已达到α，可停止迭代并进入第2 阶段；反之，令Sth=S(αNfir)，据此更新IS-PDF 的参数，并返回步骤1。此处，α 的取值越大，IS-PDF 的参数越接近最优值，但对应的迭代次数、所消耗的样本数量和计算时间也会增加。因此，为了兼顾IS-PDF 参数寻优的代价和后续可靠性指标计算的加速效果，α 的典型值可取0.05 或0.1［14］。

参数更新公式如下。

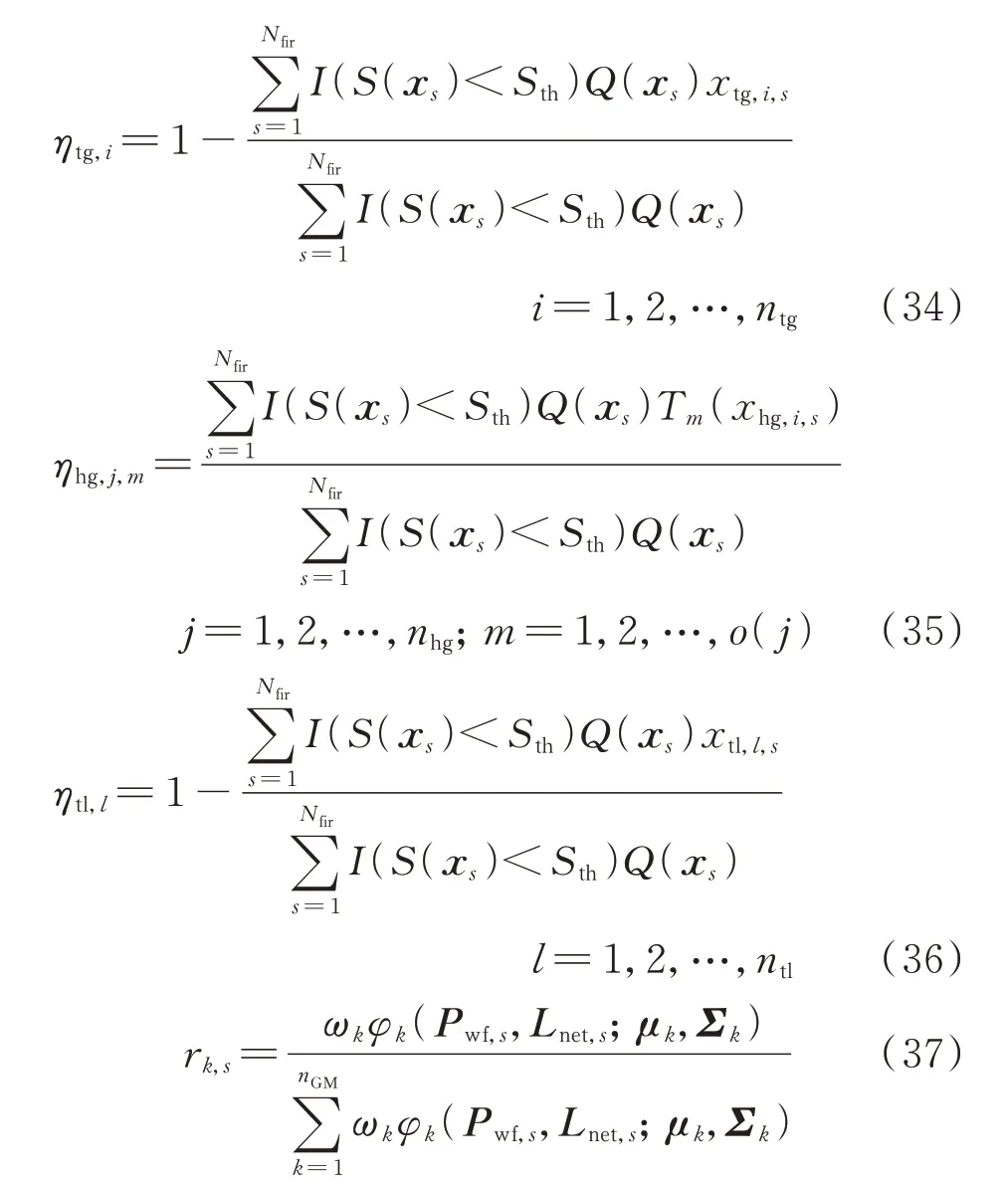
式中：下标s 表示第s 个样本对应的值；rk，s为更新连续变量IS-PDF 参数时使用的中间变量。

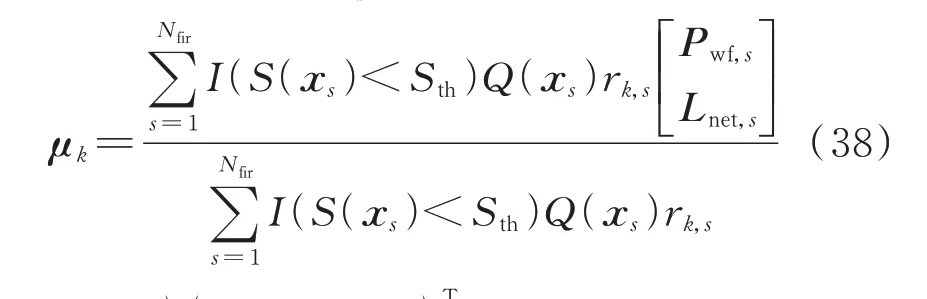
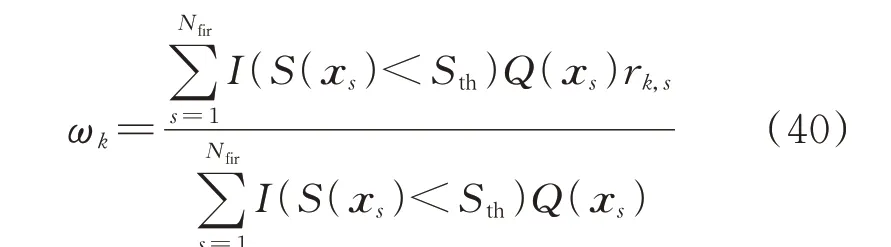
另外，需要说明的是，IS-PDF 的参数更新必须按照式（37）—式（40）的顺序进行。式（37）中用到的ωk是来自上一轮迭代的结果，而式（38）—式（40）中用到的参数都是本轮迭代更新过后的数值。如果第k 个分量的权重ωk小于1/Nfir，则删除该分量。

3）利用IS-PDF 估计可靠性指标

记第2 阶段正式估计可靠性指标时的样本容量为Nsec，将Sth固定为0。LOLP 的样本估计式为：

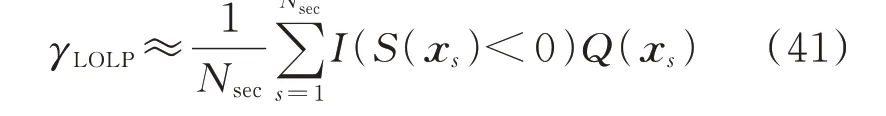
此外，电力系统各类非时序可靠性指标都可由本文所提算法进行估计，包括电力不足期望值（expected power not supplied，EPNS）γEPNS、切负荷持续时间期望值（expected duration of load curtailments，EDLC）γEDLC、电量不足期望值（expected energy not supplied，EENS）γEENS等，其样本估计的表达式与LOLP 的表达式十分相似，具体可表示为［32］：

式中：T 为统计可靠性指标的时段长度，常取1 年，即8 760 h。

若需要用方差系数判断上述可靠性指标估计的精度，则需计算数次可靠性指标，并将每一次结果视作一个样本，从而直接计算可靠性指标的样本方差和方差系数，对应公式如下。

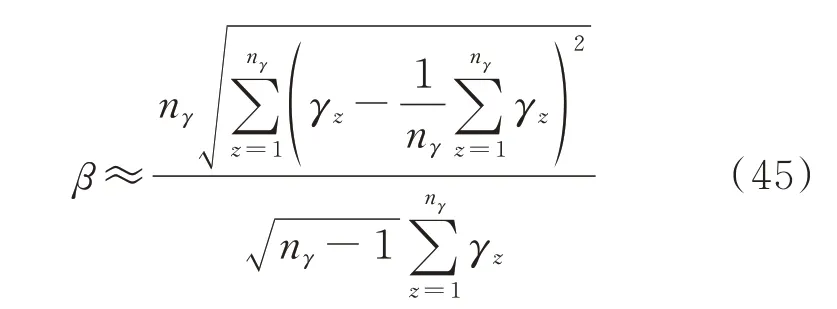
式中：β 为可靠性指标的方差系数；γz表示重复计算过程中，第z 次计算得到的可靠性指标的数值；nγ为可靠性指标重复计算的次数。

NSIS 法计算含可再生能源电力系统的靠性指标的算法流程如附录A 所示。

3.2.2 计及水文特性的电力系统可靠性指标算法设计

如果水电机组来水量和水头在丰水期和枯水期差距较大，可按如下方法计算可靠性指标：

步骤1：将丰水期和枯水期占全年总时长的比例记为pwet和pdry。

步骤2：利用3.2.1 节所述NSIS 法分别计算在丰水期和枯水期电力系统的可靠性指标，并记为γwet和γdry。

步骤3：对丰水期和枯水期的可靠性指标进行加权求和，得到全年可靠性指标γall，即

其中，在丰水期和枯水期时段内利用NSIS 法计算可靠性指标的流程区别只在于：随机变量xhg、Pwf和Lnet的原始PDF 参数是用各自时段内的历史数据拟合得到的。

4 算例分析

4.1 算例环境和基本参数设置

硬件环境：CPU 为Intel core i7-5500U、内存为16 GB 的微机。软件环境：MATLAB 2016a。

采用IEEE RTS-79 标准测试系统的基本网架结构和数据作为基础［33］，在该系统的节点1、2 和13处分别接入一座风电场，在节点18 处接一座光伏电站，构成改进IEEE RTS-79 系统。

根据测试系统的数据可知，所有离散元件的状态中，发生概率的最小值为pdv，min=3.423 5×10-4，因此建议NSIS 法中第1 阶段样本数Nfir≥29 210。故可取Nfir=30 000。此外，令反映第1 阶段缺电样本比例要求的参数α=0.05。

在标准IEEE RTS-79 系统中，所有节点负荷完全正相关，但节点18 接入光伏电站后，其净负荷与其他节点负荷不会继续完全正相关。因此，本文将除节点18 外所有节点负荷之和视作一个随机变量，将节点18 的净负荷单独视作一个随机变量，再加上3 座风电场的随机出力，故本文算例共设计有5 个连续随机变量。

风电场、光伏电站的某年度历史出力数据见文献［34］。其中，3 座风电场的原始边际PDF 见图1。

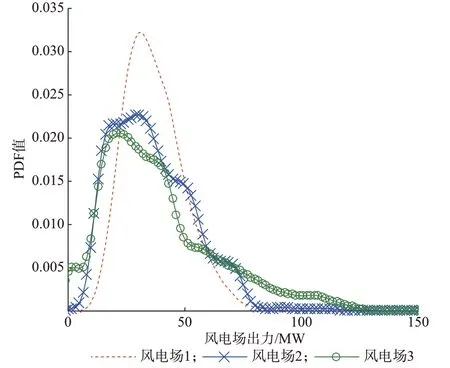
图1 3 座风电场原始边际PDF 的GMM 拟合结果Fig.1 GMM fitting results of original marginal PDF for three wind farms

4.2 历史数据相关性控制

后续算例中将会讨论风电场间相关性、风电出力与负荷的相关性对电力系统可靠性的影响，因此需要人为给定和改变连续变量的相关系数矩阵。具体操作方式如下。

首先，假设各风电场出力变量间的相关系数相同，均为ρW；各风电场出力与各负荷变量的相关系数也相同，均为ρLW；2 个负荷变量的相关系数记为ρL。按照风电场1、风电场2、风电场3、节点18 净负荷、系统内剩余负荷的顺序排列5 个连续随机变量，则其线性相关系数矩阵ρ 可表示为：

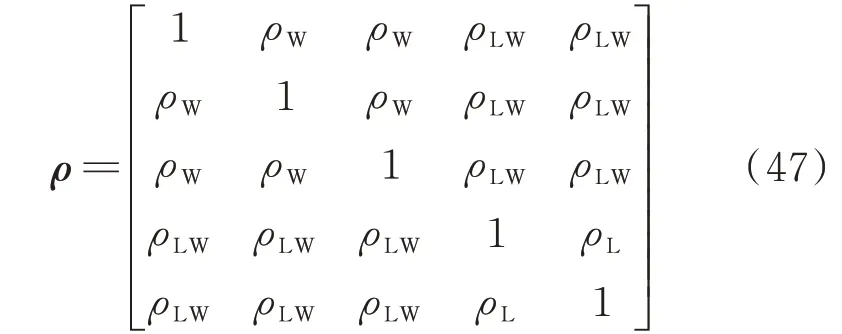
然后，参考式（13）和式（14）所述的相关性控制方法，调整历史数据的排序，即可在不改变各连续变量的边际PDF 的前提下，让其拥有指定的相关系数矩阵。随后，这些经过相关性控制的历史数据就作为式（27）的输入数据，用于建立电力系统连续变量的联合PDF。

4.3 NSIS 法的正确性验证

为验证NSIS 法计算结果的正确性，需将其与其他方法的计算结果作对比。本节将基于简单随机采样的MCS 法记为方法1，LHS 法记为方法2，文献［13］中提出的基于交叉熵的IS 法记为方法3。

采用NSIS 法与上述几种方法来计算改进IEEE RTS-79 系统的LOLP、EDLC、EPNS、EENS等可靠性指标。对于方法3，将其第1 阶段（预抽样）的样本容量设置为30 000，与NSIS 法保持一致。将所有方法的收敛条件均设置为所计算的可靠性指标的方差系数小于等于0.02。各方法重复50 次后的计算结果平均值如表1 所示。

由表1 可知，在相同收敛条件下，NSIS 法与其他3 种方法计算出的改进IEEE RTS-79 系统的4 种可靠性指标基本一致，进一步验证了NSIS 法的正确性。

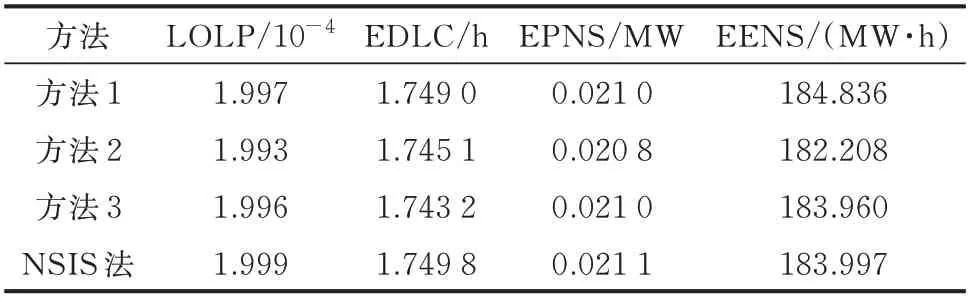
表1 4 种方法评估改进IEEE RTS-79 系统可靠性的结果对比Table 1 Result comparison of four methods for evaluating reliability of improved IEEE RTS-79 system

4.4 NSIS 法的性能验证

4.3 节提到的4 种方法按照方差系数小于等于0.02 的要求重复计算50 次可靠性指标，其消耗样本和计算时间的平均值如表2 所示。

表2 4 种方法评估改进IEEE RTS-79 系统可靠性的计算成本对比Table 2 Comparison of calculation costs of four methods for evaluating reliability of improved IEEE RTS-79 system

由表2 可知，在同样的精度要求下，NSIS 法消耗的样本数和计算时间远小于MCS 法和LHS 法。由于包含了分层抽样思想，在计算4 种可靠性指标时，NSIS 法相较于单纯的交叉熵IS 法，计算用时缩短了20.3%～30.4% 不等，计算效率得到了显著提升。

此外，为验证NSIS 法在不同可靠性水平的电力系统中的适应性，将上述4 种方法的样本容量均设置为80 000 次，对LOLP 指标的方差系数进行关于负荷水平（即系统可靠性水平）的灵敏度分析。其中，根据4.3 节计算过程可知，方法3 和NSIS 法在计算该测试系统时，需要在预抽样阶段迭代2 次，共消耗2Nfir=60 000 次样本。此外，方法1 和方法3 采用式（3）计算方差系数，方法2 和NSIS 法采用式（45）计算方差系数。结果如图2 和图3 所示。

由图2 可知，随着负荷水平的降低，系统内发电资源的充裕度将逐渐提高，在可靠性水平上表现为LOLP 绝对值下降，即系统缺电这一小概率事件发生的概率进一步降低。

图2 LOLP 关于负荷水平的关系图Fig.2 Relation diagram of LOLP with respect to load level

由图3 可知，在LOLP 数值下降的情况下，各方法采样20 000 次后的计算结果的方差系数均逐渐变大，但NSIS 法相较于其他方法而言，方差系数总是最小的（即精度最高），且受可靠性水平的影响也最不明显。这说明NSIS 法比其他3 种方法更适合用来评估现代高可靠性电力系统的可靠性。

图3 方差系数关于负荷水平的关系曲线Fig.3 Relation curves of coefficient of variance with respect to load level

4.5 变量相关性对系统可靠性水平的影响

储能设备和需求响应技术的大规模应用，可实现源荷匹配，促进新能源消纳。这一背景下，含储能的新能源场站出力与计及需求响应的负荷之间的相关性水平可能会有明显提升，因此，需分析源荷相关性水平对系统可靠性水平的影响规律。

将式（47）中的ρL固定为0.6，让ρLW和ρW在区间［0，0.6］内变化，并求出对应的LOLP 值。绘制三者的函数关系如图4 所示。需要说明的是，图4 中留白部分的任意一点的坐标代入式（47）后得到的矩阵都是非正定的，而相关系数矩阵必须是正定的，故留白区域无法进行可靠性计算，也就没有对应的LOLP 值。

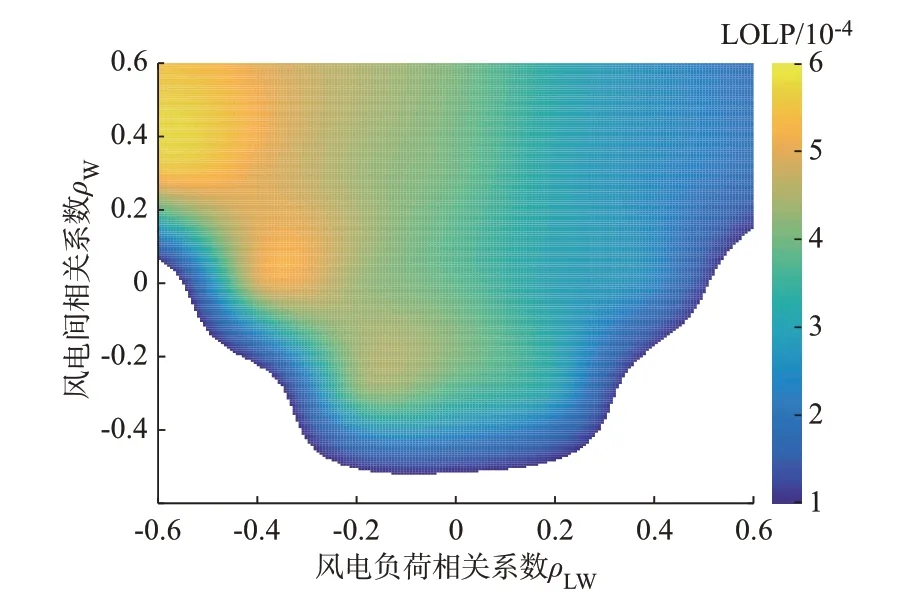
图4 各变量相关性水平对系统可靠性的影响Fig.4 Influence of correlation level of each variable on system reliability

由图4 可知，风电场出力与负荷的相关性越高，系统的可靠性越高。而各风电场出力的相关性越高，系统的可靠性越低。

4.6 计及水文特性的可靠性指标评估

本节中将改进IEEE RTS-79 测试系统中节点22 所接的6 台装机容量为50 MW 的火电机组替换为相同容量的水电机组，利用3.2.2 节所述方法计算计及水文特性的可靠性评估指标。

首先，根据中国青海地区实际水电出力数据，利用K-means 方法对该地区丰水期、枯水期水电机组出力水平进行聚类。其中，青海地区水电丰水期为每年4 月1 日至10 月31 日，剩余时间均属于枯水期，故式（46）中的pwet和pdry分别为0.586 3 和0.413 7。

在丰水期、枯水期时段内将水电机组出力数据分别聚类为3 类，即对应3 个出力水平。此外，还应考虑机组故障状态下的出力为0。因此，水电机组的出力水平在丰、枯水期均可用4 种状态模型表征，其数值和对应的概率大小如表3 所示。

表3 丰水期、枯水期水电机组出力水平和对应概率Table 3 Power output levels and corresponding probabilities of hydro power units during wet and dry periods

表3 中出力水平以标幺值形式给出，对应的基准值为水电机组的装机容量。按照3.2.2 节所述方法，分别采用NSIS 法计算丰、枯水期的LOLP 指标，其数值分别为8.587 0×10-5和1.268 3×10-3。利用式（46）求取电力系统全年LOLP 指标为5.750 4×10-4。与表1 对比可知，由于火电机组被含有多个降额状态的水电机组代替，系统发电资源可用容量必然减少，可靠性下降，故LOLP 值增大。

5 结语

本文以含可再生能源电力系统的可靠性指标计算方法为研究对象，提出了一种非参数重要性分层抽样法。该方法考虑到IS 法与LHS 法优缺点互补的特性，利用两者的结合实现了电力系统可靠性指标计算的进一步加速。

本文首先分析了IS 法与LHS 法结合时面临的矛盾和困难。然后，选择GMM 作为非参数形式的IS-PDF，利用GMM 各分量均为易于提取相关系数矩阵的多元正态分布的特点，为GMM 定制了计及相关性控制的LHS 法采样方案，从而在不牺牲IS 法与LHS 法各自效率的同时，实现了两者的结合，即本文所提出的NSIS 法。设计算例验证了所提NSIS 法在含可再生能源电力系统可靠性评估中的正确性和有效性，相关结论如下：

1）将NSIS 法和MCS 法、LHS 法以及基于交叉熵的IS 法同时用于计算测试系统的可靠性指标。结果显示NSIS 法计算结果与其他3 种算法基本一致，但效率高于其他3 种算法，说明了NSIS 法的正确性和有效性。

2）NSIS 法的精度受可靠性指标绝对值大小的影响较小，因此适用于高可靠性电力系统。

3）新能源出力与负荷的正相关性有助于系统可靠性的提升，而新能源出力之间的相关性过高则会损害系统可靠性。因此，可从这一结论出发，利用大规模储能技术和需求响应技术控制新能源出力间、新能源出力与负荷的相关性，从而提升系统的可靠性。

本文在撰写过程中得到江苏省配电网智能技术与装备协同创新中心开放基金资助项目(XTCX202001)和南京工业大学引进人才科研启动专项经费(39810127)资助，特此感谢！

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。