采用辅助变压器的可调压谐振零电压零电流开关变换器

李彬彬，王志远，张丙旭，赵晓东，徐殿国

（哈尔滨工业大学电气工程及自动化学院，黑龙江省哈尔滨市 150001）

0 引言

截至2020 年，中国风电装机容量达到281 GW，光伏装机容量达到253.4 GW，分别同比增长34.6%和24.1%［1］，新能源发电增速显著；另一方面，数据中心的机架总规模达到314.5 万架，同比增长39%［2］，电动汽车充电桩总量达到167.2 万台［3］，直流用电终端增长迅速，源、荷的直流特征越来越明显。该趋势下，直流配电技术以其线路损耗小、供电可靠性高、分布式能源/柔性负荷更易接入的优势，逐渐受到广泛关注［4-6］。研究适用于大功率高效率的DC/DC 变换器是发展直流配电网的关键。

移相全桥变换器利用变压器原边漏感和开关管结电容的谐振可以实现原边开关管的零电压开通，具有较高的功率密度，在大功率场景中应用广泛［7-9］。但是，由于其滞后桥臂在轻载的情况下易丢失零电压特性，原边存在关断损耗，副边存在整流管的反向恢复损耗等问题，变换器的整体效率较低［10-12］。通常采用拓扑结构改造［13-14］和控制方法优化的方法［15］缓解上述问题。

相比之下，以LLC 变换器为代表的谐振变换器可以在全负载范围内实现开关管的零电压开通、准零电流关断以及二极管的零电流关断，具有效率高的特点［16-17］。为了实现调压功能，LLC 变换器通常采用变频控制方法［18］，本质是通过调节开关频率改变谐振腔阻抗［19］。开关频率的变化增加了电路电磁兼容和滤波器的设计难度［20］。变压器需要按照最低开关频率进行设计，其体积、重量、成本和损耗均有所增加，不适合应用于大功率场景。文献［21］使用了移相与变频结合的方式，利用零电平对励磁电流峰值进行限制，使变压器可以按照额定工作频率设计，但是只有在输入、输出电压匹配时，才能实现软开关。

为解决变频控制的问题，可以采用移相［18，22］或者改变占空比［23］的控制方式。2 种控制方式均是通过调整谐振腔两端的电压实现对电压增益的调节，但是需要开关管关断较大的电流，开关损耗较大。在大功率场景中，绝缘栅双极型晶体管（IGBT）是最常用的开关器件，其存在的拖尾电流进一步导致关断损耗较大，上述控制方式并不适用。文献［24］使LLC 变换器工作于定频开环模式，通过在前级或后级增加由Buck 或Boost 变换器组成的调压器进行电压增益调节，但是调压器一般为硬开关电路，效率较低。文献［25-26］将双向开关并联至变压器副边或者原边构造出类似Boost 的升压结构，实现电压调节，但是该双向开关为硬关断，且关断电流较大，增加了损耗。文献［27-29］使用2 个变压器以及辅助开关，通过辅助开关和辅助变压器使输出侧整流器获得额外的电压增益。辅助变压器仅承担有限的功率等级，但是需要具有与主变压器相同的绝缘水平，在电压变比较大的场合下，辅助变压器的体积较大。

本文提出了一种采用辅助变压器的可调压谐振零电压零电流开关（zero-voltage zero-current switching，ZVZCS）变换器，在传统LLC 变换器的基础上增加了辅助变压器和辅助半桥，变换器一、二次侧开关管均工作在固定开关频率、50%占空比之下。通过调节二次侧辅助半桥开关管和一次侧开关管的移相角度，可以调整辅助变压器参与升压的时间，实现对电压增益的调节。同时，实现了一次侧开关管的零电压开通和准零电流关断，二次侧二极管的零电流关断，辅助半桥开关管的零电压开通。辅助变压器仅位于低压侧，降低了变压器的绝缘需求和体积。本文详细分析了所提拓扑的电路特点、工作原理、参数设计方法。通过仿真和实验验证了该拓扑结构的正确性。

1 变换器工作原理简介

1.1 变换器拓扑构成

如图1 所示，采用辅助变压器的可调压谐振ZVZCS 变换器电路主要由5 个部分构成：一次侧电路、二次侧电路、LC 谐振腔、主变压器Tr1以及辅助变压器Tr2。一次侧电路包含由4 个开关管构成的全桥和1 个输入电容；二次侧电路包含由4 个二极管构成的全桥、2 个开关管构成的辅助半桥和1 个输出电容；谐振腔中Lr为变压器Tr1和Tr2的漏感并作为谐振电感参与谐振，Cr为谐振电容。

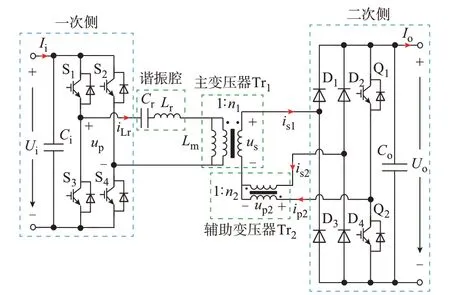
图1 所提变换器拓扑结构Fig.1 Topology of proposed converter

当变换器正常工作时，一次侧开关管S1、S4同开同关，开关管S2、S3同开同关，同一桥臂的两开关管之间存在一定的死区时间。二次侧辅助半桥中开关管Q2的驱动信号与S1、S4的驱动信号存在一定的移相角α。全桥输出电压up为高频方波电压，其频率为开关频率fs，运行周期为Ts，幅值为输入电压Ui，Uo为经谐振腔和二次侧整流输出的直流电压。

为了便于后续的原理分析，做出如下假设：输入、输出电容Ci、Co足够大以保证Ui、Uo电压恒定；变压器Tr1、Tr2为理想变压器，变比分别为n1、n2；忽略电路中其他寄生参数。

1.2 工作模态分析

采用辅助变压器的可调压谐振ZVZCS 变换器主要工作波形如图2 所示。

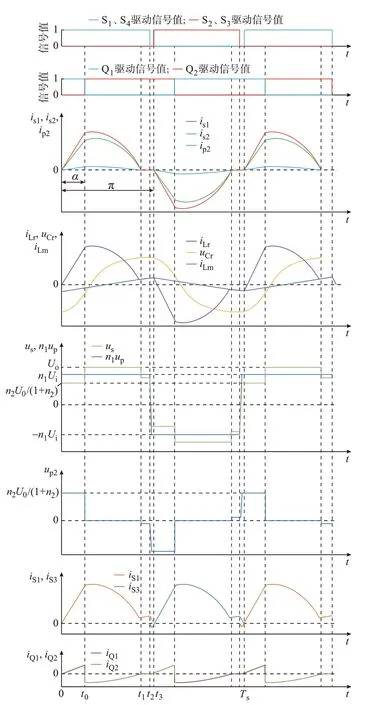
图2 可调压谐振ZVZCS 变换器主要工作波形Fig.2 Main working waveforms of voltage-regulatable resonant ZVZCS converter

图2 中：is1为主变压器Tr1副边电流；ip2、is2分别为辅助变压器Tr2原、副边电流；iLr、uCr、iLm分别为谐振电感电流、谐振电容电压及主变压器Tr1励磁电感电流；u1、us分别为一次侧全桥输出电压和主变压器副边电压；up2为辅助变压器原边电压；iS1、iS3、iQ1、iQ2分别为流经开关管S1、S3、Q1、Q2的电流。一次侧开关管开关频率和占空比保持固定，通过控制二次侧辅助开关管Q2与一次侧开关管S1、S4的移相角α可以调节辅助变压器参与对输出电压进行升压的时间，实现对电压增益的调节，移相角越大，辅助变压器参与升压的时间越长，电压增益越大。变换器在半个周期中存在2 种谐振状态，对应的各个阶段的等效电路图如图3 所示，一、二次侧导通电流的器件和线路分别用紫色和蓝色线条进行了突出强调。

1）［0，t0］阶段：该阶段的等效电路如图3（a）所示。S1、S4导通，S2、S3关断，D1、D4导通，D2、D3反向偏置关断。辅助半桥开关管Q1开通，Q2关断。辅助变压器Tr2的原边电压等于主变压器Tr1的副边电压us，二次侧的输出电压Uo由主变压器Tr1的副边电压us和辅助变压器Tr2的副边电压us/n2组成。进一步得出主变压器Tr1的副边电压us=n2Uo/(1+n2)＜n1Ui。Lr和Cr发生谐振，电路工作在第一谐振状态，iLr、is1、ip2、is2谐振变化，电流值逐渐从零增大。谐振电容电压uCr从负的最大值开始正向增大。流经开关管Q1的电流为流经二极管D4电流的1/n2。

2）［t0，t1］阶段：该阶段的等效电路如图3（b）所示。经过一定的移相角α，在t0时刻，Q2导通，Q1关断，关断过程为硬关断。但是关断电流较小，仅为主变压器副边电流的1/（1+n2）。在Q1、Q2驱动信号的死区时间内，Q1、Q2快速完成换流过程，电流is2流过Q2反并联二极管，Q2实现零电压开通。该阶段辅助变压器Tr2两端电压始终为零，不起作用，主变压器Tr1副边电压us=Uo＞n1Ui。Lr和Cr进入第二谐振状态，谐振电容电压uCr继续上升。

3）［t1，t2］阶段：该阶段的等效电路如图3（c）所示。在t1时刻，第二谐振状态结束，谐振电流iLr减小到与励磁电感电流iLm相等，二次侧电流is1、ip2、is2降低到零，D1、D4自然关断。在该时间段内，is1、ip2、is2维持为零。谐振电容电压uCr到达最大值UCrm。

4）［t2，t3］阶段：该阶段为一次侧开关管的死区时间，运行阶段的等效电路如图3（d）所示。t2时刻，S1、S4关断，其关断电流为电流值很小的励磁电感电流iLm，实现了准零电流关断。S1、S4关断后，励磁电感电流将会对一次侧开关管S1、S2、S3、S4结电容进行充放电，使得开关管S1、S4的结电容电压上升为Ui而开关管S2、S3的结电容电压下降到零，因而t3时刻，S2、S3可以实现零电压开通。

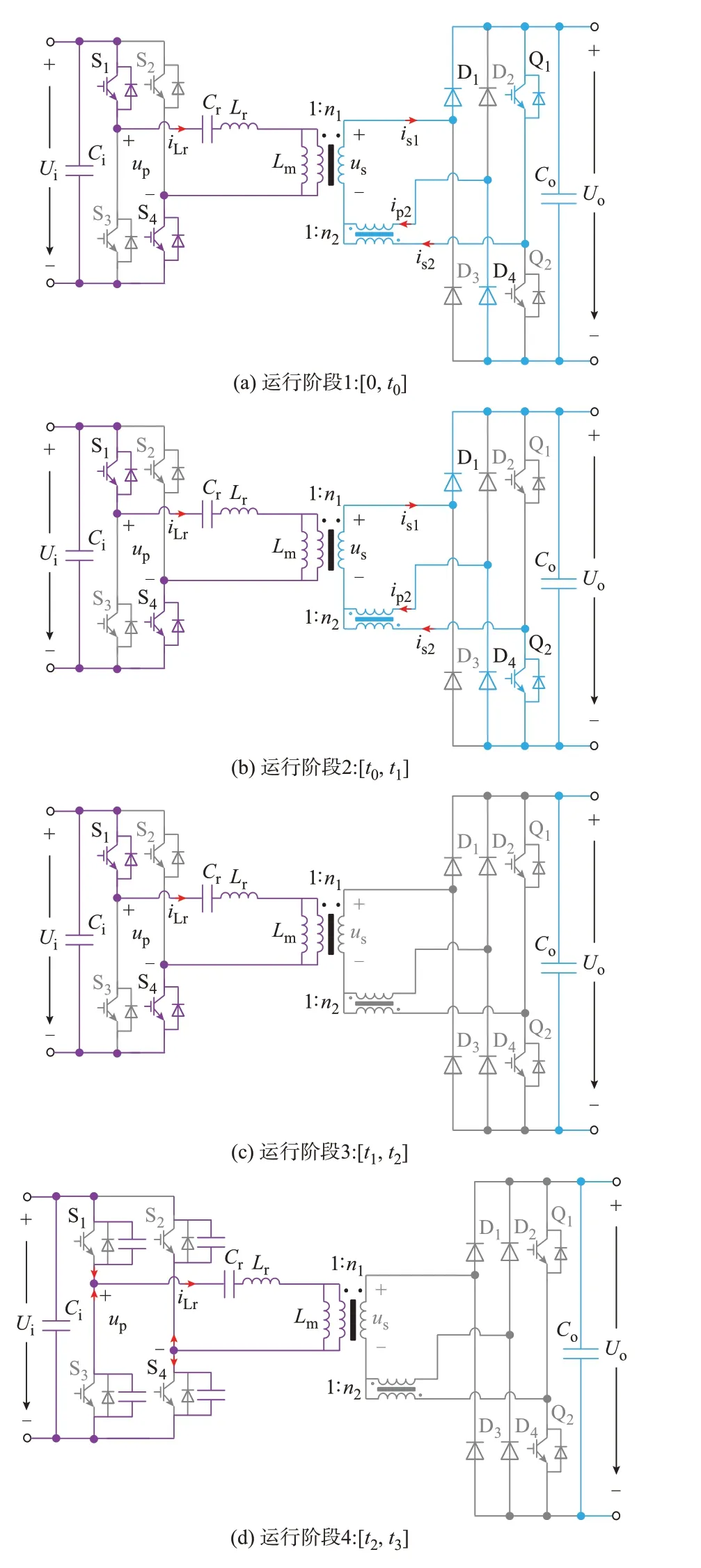
图3 可调压谐振ZVZCS 变换器各运行阶段等效电路Fig.3 Equivalent circuits of voltage-regulatable resonant ZVZCS converter in each operation stage

后半周期工作模态与前半周期镜像，因而不再赘述。综合上述分析，通过引入辅助变压器和辅助开关，一次侧电路的开关管S1至S4均实现了零电压开通和准零电流关断，二次侧电路的二极管D1至D4实现了零电流关断，辅助半桥的开关管Q1至Q2实现了零电压开通。

2 电路分析及参数计算

2.1 增益分析

对于移相控制的谐振DC/DC 变换器，常规的基波等效法不再适用，本文将利用谐振腔的状态平面轨迹［22］来进行分析。半个周期内谐振腔2 种谐振状态的简化等效电路如附录A 图A1 所示。

第一谐振状态（［0，t0］阶段）对应的等效电路如附录A 图A1（a）所示。该状态下，主变压器原边电压为Uon2/［n1（n2+1）］，谐振腔两端电压为Ui-Uon2/[n1(n2+1)]，在零时刻，谐振腔的电流iLr为零，谐振电容电压为最大值-UCrm，通过对等效电路列写基尔霍夫电压定律（KVL）方程可得谐振电容电压和谐振电流的表达式为：

第二谐振状态（［t0，t1］阶段）对应的等效电路如附录A 图A1（b）所示。该状态下，二次侧的辅助变压器不起作用，谐振腔两端电压为Ui-Uo/n1。t1时刻，谐振电流iLr降低到零，谐振电容电压达到最大值UCrm，同上一谐振状态分析过程，通过对等效电路列写KVL 方程，可得谐振电容电压和谐振电流的表达式为：

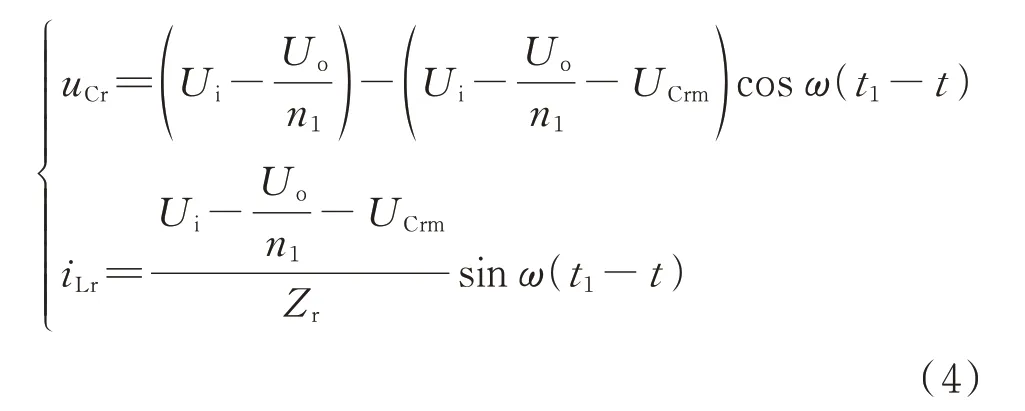
根据式（4），谐振腔的第二谐振状态可以表示为以（O2，0）为圆心、r2为半径、（UCrm，0）为终点的一段圆弧，角度为θ，如图4 中弧BC 所示。其中，O2和r2的表达式为：

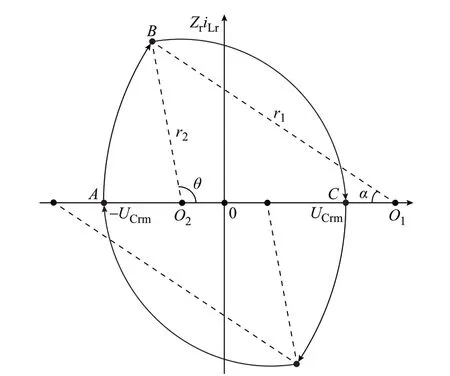
图4 谐振腔状态平面轨迹Fig.4 State-plane trajectory of resonant cavity

当移相角等于零时，Uo=n1Ui。取Ui=1 000 V，n1=0.3，n2=4，Lr=10 μH，Cr=25 μF，fs=10 kHz，根据式（11），可以得到输入功率P、电压增益M 与移相角α 之间的对应关系如附录A 图A2 所示。

当α=0 时，Q2与S1、S4同开同关，辅助变压器两端电压始终为零，对输出电压没有调节作用，变换器相当于一个传统LLC 谐振变换器，输出增益为主变压器变比n1。当α=π 时，Q2与S1、S4无重叠时间，辅助变压器在整个谐振周期都起作用，相当于在LLC谐振变换器输出侧增加了一级增益为1+1/n2的升压环节，变换器总增益为n1（1+1/n2）。当0 ＜α ＜π时，变换器处于移相控制模式，电压增益随着α 的增大而增大。因此，通过对移相角α 的控制可以实现对电压的调节，同时保证一次侧开关管的零电压开通、零电流关断和二次侧二极管的零电流关断。

2.2 谐振电流峰值分析

谐振电流的峰值对应变换器状态平面轨迹图在纵轴投影的最大值。当移相角α 从0 到π 变化时，谐振电流峰值出现的位置存在3 种情况，如附录A 图A3 所示。

当α ＜π/2，θ ＞π/2 时，如附录A 图A3（a）所示，谐振腔的第一谐振状态对应角度小于π/2 的圆弧，第二谐振状态对应角度大于π/2 的圆弧。该情况下，谐振电流的峰值出现在第二谐振状态中，对应图中红色箭头位置，峰值电流为r2/Zr。

当α ＜π/2，θ ＜π/2 时，如附录A 图A3（b）所示，2 种谐振状态对应的圆弧均小于π/2。该情况下，谐振电流峰值出现在2 种谐振状态的交点位置，峰值电流为（r1sin α）/Zr=（r2sin θ）/Zr。

当α ＞π/2，θ ＜π/2 时，如附录A 图A3（c）所示，该情况下，谐振电流峰值出现在第一谐振状态，峰值电流为r1/Zr。

代入上节所列的具体参数，可以得到谐振电流峰值iLr，max随移相角α 的对应关系，如附录A 图A4所示，谐振电流峰值随着移相角α 从0 到π 变化，呈现先增大后减小的趋势。

基于对电流峰值和电路结构的分析，一次侧开关管的最大电流应力即为谐振电流峰值ILr，max，二次侧二极管的最大电流应力为ILr，max/n1，二次侧辅助开关管的最大电流应力为ILr，max/［n1（1+n2）］。

2.3 变压器变比n1和n2

由2.1 节分析可知，变换器的增益范围为n1～n1（1+1/n2），电压调节范围为1/n2。可以看出，变比n1决定了变换器的最小增益，变比n2决定了变换器的电压调节范围。因此，变比n1和n2应满足：

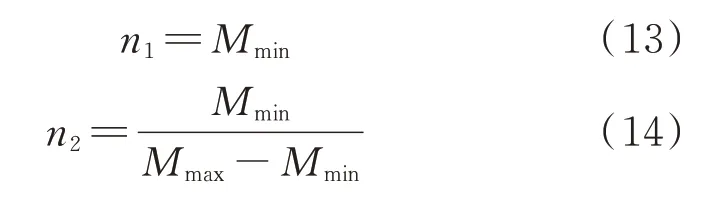
式中：Mmin和Mmax分别为变换器的最小和最大电压增益。

当变比n2减小时，可以增大变换器的电压调节范围。但是由1.2 节可知，辅助半桥所流过的电流为主变压器副边电流的1/（1+n2），当变比n2减小时，辅助半桥的开关管流过的电流增大，其导通损耗和关断损耗均会增大，使变换器效率下降。以关断损耗为例，辅助半桥开关管的关断电流Ioff可表示为：

通过式（7）消去移相角α，并代入具体参数可得Ioff与辅助变压器变比n2的对应关系，如附录A 图A5所示。由图A5 可以看到，Ioff随着n2的增大而减小。当n2＜1 时，辅助开关的关断电流达到了300 A 以上，比n2取4 时的关断电流增大了一倍以上，关断损耗大幅增加。因此，辅助变压器的变比n2应在满足电压调节范围需求的基础上取尽量大的数值。

2.4 谐振腔参数设计

谐振腔中的谐振电感由主变压器漏感Lleak1和辅助变压器的漏感Lleak2组成。对于辅助变压器的漏感，可以建立如附录A 图A6 所示的2 种谐振状态下辅助变压器的等效电路进行分析。图A6 中up为主变压器原边电压，uTr2p和uTr2s分别为辅助变压器的原、副边绕组的电压，is2和ip2分别为流过辅助变压器原、副边的电流。辅助变压器原、副边的电压和电流满足uTr2p∶uTr2s=n2∶1 和ip2∶is2=1∶n2。

第一谐振状态辅助变压器的等效电路如附录A图A6（a）所示。二次侧电路的电压、电流和漏感均折算到一次侧，辅助变压器漏感位于副边。对等效电路列写KVL、基尔霍夫电流定律（KCL）方程可得：

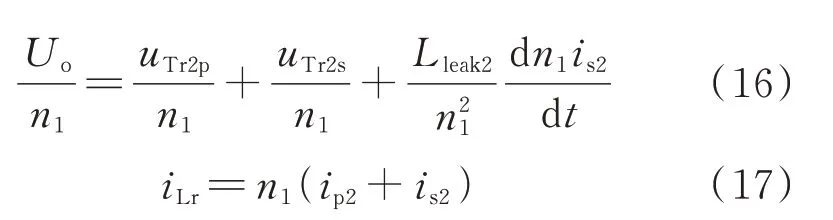
式中：Td为死区时间；Coss为开关管的输出电容。

3 仿真分析

为验证本文所提拓扑的原理以及参数设计的正确性，本文搭建了1 kV 降压至311 V、功率为100 kW 的仿真模型，具体仿真参数见附录A 表A1。在该场景下，综合变换器的功率密度与开关损耗等因素，开关频率选取在10 kHz。

变换器在输入电压变化工况下ui、uo、iLr、uCr、ip2、is1、is2的波形如附录A 图A7 所示。输入电压ui初始为850 V，在0.05 s 开始逐渐上升，最终在0.25 s 稳定于1 000 V，可以看出输出电压uo在闭环控制下始终保持在311 V，变换器电压增益由0.366 下降到0.311，移相角由127.90°减小到30.45°，与式（11）的理论结果仅有不到3%的误差。谐振电流的峰值由215.4 A 降低到229.1 A，分别对应附录A 图A3（b）和（a）的情况，且与理论计算结果基本一致。

在输入电压为1 000 V 的额定工况下，变换器稳态工作的详细波形如附录A 图A8 所示。由仿真结果可以看出，一次侧S1、S4导通，二次侧Q1导通时，辅助变压器原边电压与主变压器副边电压相等均为247 V，与理论结果一致，谐振电流和谐振电容电压上升。经过一定的移相角度（α=30.45°）之后，Q2导通、Q1关断，关断电流为154 A，仅为副边谐振电流的1/5。谐振腔进入第二谐振状态，辅助变压器电压为0 V，谐振电流峰值为229.1 A。第二谐振状态结束时，谐振电流为零，谐振电容电压上升至最大值101.8 V，与式（10）理论分析结果一致。

在额定工况下开关管S1和Q2的驱动信号及其电压、电流（uS1、uQ1、iS1、iQ2）的波形如附录A 图A9 所示。可以看出，在S1驱动信号来临之前，开关管S1的电压便已经减小为零，实现了零电压开通，当S1关断时仅关断很小的励磁电流，因而一次侧开关管可以实现零电压开通和准零电流关断。对于二次侧的开关管，开关管Q2存在关断电流，但相对主变压器副边电流较小，导通前开关管电压降为零，实现了零电压导通。

为验证本文所提拓扑的效率优势，本文进行了与使用调频控制的传统LLC 谐振变换器在100 kW功率等级下的效率仿真对比。其中，一次侧IGBT器件选择5SNG 0450R170300、二次侧二极管器件选择5SED 0890T2240、辅助开关管选择英飞凌的FF200R06KE3。LLC 谐振变换器的谐振电容大小为2.4 μF，K 值选择为3，谐振电感和励磁电感大小分别为110 μH、330 μH，变压器变比为0.3。对比结果如图5 所示。

图5 所提拓扑与调频控制LLC 变换器的效率曲线Fig.5 Efficiency curves of proposed topology and frequency regulation controlled LLC converter

由图5 可以看到，本文所提拓扑具有优于传统LLC 谐振变换器的效率。经典的LLC 谐振变换器需通过改变开关频率来实现调压，为限制开关频率变化范围、保证变压器体积不至于过大，励磁电感与谐振电感的比值K 通常设计得较低，即励磁电感较小。这导致谐振过程结束时开关管需要关断的励磁电流比较大。由于大功率下通常使用IGBT 作为开关器件，存在拖尾电流问题，当关断的电流较大时，其关断损耗较为严重。相比之下，本文所提拓扑的励磁电感仅需要保证在死区时间内完成开关管结电容的充放电，其电感值可以设置得比较大，因此在谐振周期结束时开关管需要关断的励磁电流很小，近似零电流关断。二次侧开关管存在关断电流但相对较小，且二次侧电路电压等级较低，关断损耗较小。因此，在大功率场景下，本文所提拓扑具有更高的效率。

4 实验分析

为进一步验证本文所提拓扑的有效性，本文搭建了输入电压为333 ～400 V、输出电压为200 V、功率等级为2.5 kW 的实验平台，照片如附录A 图A10 所示，具体实验参数如附录A 表A2 所示。本文详细记录了输入电压为350 V 和375 V 的实验波形。

输出电压为350 V 工况下，开关管S1和Q2的驱动电压、一次侧全桥输出电压u1、主变压器副边电压us1和辅助变压器原边电压up2如图6（a）所示，谐振电流iLr、谐振电容电压uCr、主变压器副边电流is1和辅助变压器原边电流ip2如图6（b）所示。S1开通、Q2关断时，辅助变压器原边与主变压器副边并联，辅助变压器参与对变换器的升压。S1和Q2均导通时，辅助变压器原、副边均与输出电压负极连接，由于辅助变压器存在漏感，在副边电流快速下降时，辅助变压器漏感感应出负向电压，其电压幅值取决于电流变化速率。在副边电流到零后，副边二极管无反向恢复损耗，实现了零电流关断。谐振电容电压波动峰值为60 V，较理论值55.8 V 偏大。由于变换器存在损耗，其输入功率大于2.5 kW，实际测量情况下变换器的效率为94.7%。考虑效率后的谐振电容电压波动峰值理论值为58.9 V，测量值与理论值偏差在2%以内。副边开关管的移相角α=133.2°，在理论计算之下该角度对应的输出电压幅值为207 V，大于实际输出电压。在实际电路之中，IGBT 和二极管均存在导通压降，本文实验平台的导通压降值在1.5 V 左右，且原、副边均为全桥结构，开关管产生的总压降在6 V 左右，考虑上述因素之后，该移相角符合理论分析。

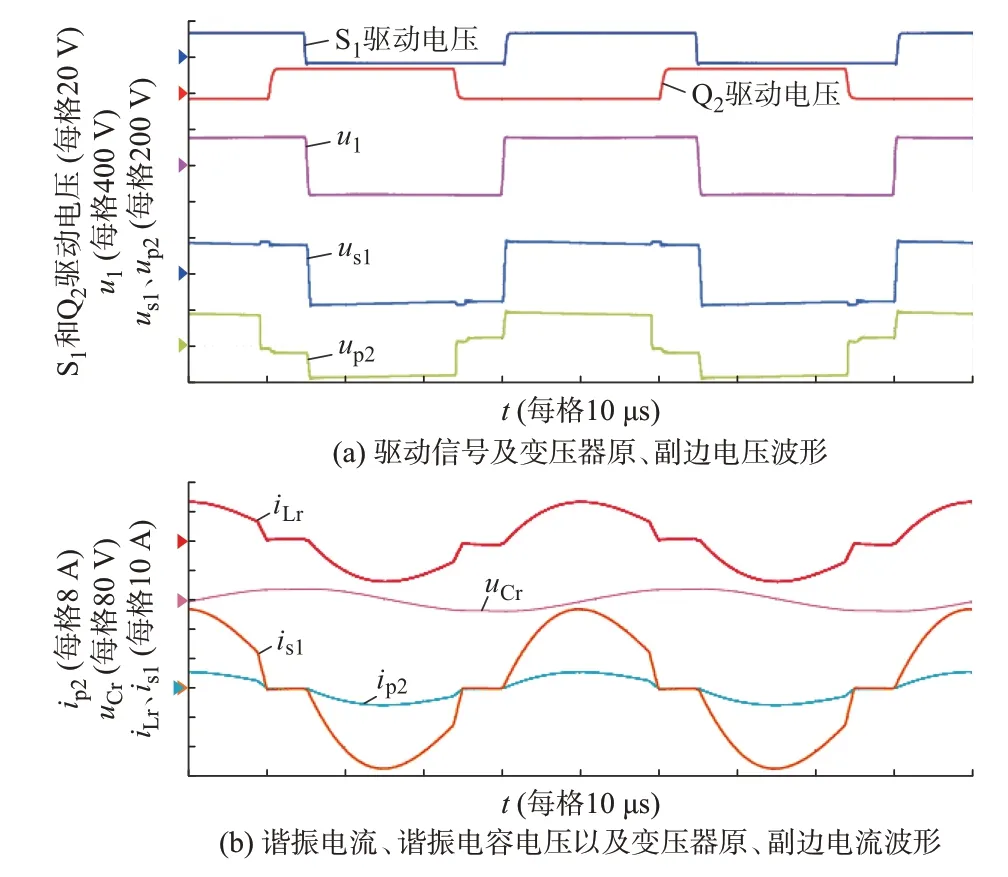
图6 稳态运行实验波形(Uo=350 V)Fig.6 Experiment waveforms in stable operation(Uo=350 V)

一次侧开关管S1的驱动电压、端电压和谐振电流的放大波形如附录A 图A11（a）所示，可以看到在开关管S1导通前，励磁电流完成了对开关管S1寄生电容电压的放电，开关管S1实现了零电压导通。在开关管S1关断时，关断电流为励磁电流，幅值仅为1 A，开关管S1实现了准零电流关断。二次侧辅助开关管Q2的驱动电压和端电压波形如附录A 图A11（b）所示，在开关管Q2导通前，辅助变压器原边电流完成了对开关管Q2结电容电压的放电，开关管Q2实现了零电压开通。

输出电压为375 V 工况下，变换器的详细实验波形如附录A 图A12 所示。由于输入电压增大，变换器所需增益降低，谐振电容电压峰值减小到57.8 V，移相角减小到68.98°，考虑到变换器的效率与开关管导通压降，上述结果与理论分析基本一致。同时，由附录A 图A13（a）、（b）可见，在实现对输出电压调节的同时，一次侧开关管仍然可以实现零电压导通和准零电流关断，二次侧开关管仍然可以实现零电压开通。很好地验证了所提拓扑的电压调节能力和软开关能力。

在400 W～3 kW 的功率范围内，实验平台分别在350、375、400 V 以及输入电压下的效率曲线如图7 所示。可以看到，在较宽的负载范围内，本文所提拓扑的效率均保持稳定，最高效率可以达到95.7%。由于变换器开关频率固定，一次侧开关管所关断的励磁电流不随负载变化，关断损耗不变，轻载下开关管的关断损耗占比增加，效率下降。另外，相比于仿真工况（100 kW），实验情况下的效率较低，主要原因在于：实验系统所使用的变压器并未针对变换器进行效率方面的优化设计；各个分散模块之间的引线存在额外的电阻；实验系统所使用的IGBT 和二极管压降均在1.5 V 左右，在实验系统功率等级下器件导通损耗占比较大。

图7 不同输入电压下的效率曲线Fig.7 Efficiency curves with different input voltages

5 结语

本文提出了一种采用辅助变压器的可调压谐振ZVZCS 变换器，通过在传统LLC 变换器的基础上增加辅助变压器和辅助半桥，可以实现对电压增益的调节功能，同时实现了开关管和二极管的软开关。本文详细分析了变换器的工作原理和谐振过程，基于谐振过程等效电路得出了谐振腔谐振状态平面轨迹图，进而得到电压增益和移相角的对应关系。在此基础上明确了谐振电容、励磁电感等参数的设计方法。变换器能够实现一次侧开关管的零电压开通和准零电流关断，以及二次侧辅助半桥开关管的零电压开通。仿真和实验结果证明了变换器的电压调节能力和开关管的软开关能力，验证了引入辅助变压器和辅助开关所带来的优势。该拓扑能够较好地满足直流配电网等应用场景对电压调控和效率的需求。下一步的研究，可探讨在大功率应用场景下拓扑的功率密度的提升。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。