考虑输入量不良数据的发电机动态状态估计方法

朱茂林，刘 灏，毕天姝，谢永胜，赵俊博

（1. 新能源电力系统国家重点实验室（华北电力大学），北京市 102206；2. 国网新疆电力有限公司，新疆维吾尔自治区乌鲁木齐市 830002；3. 密西西比州立大学电气与计算机工程学院，斯塔克维尔 39762，美国）

0 引言

同 步 相 量 测 量 单 元（synchrophasor measurement unit，PMU）的广泛应用为电力系统暂态稳定分析与控制提供了重要信息来源，为精确跟踪电力系统机电暂态过程提供了新的技术手段［1-3］。然而，在应用过程中PMU 量测随机误差和不良数据的存在可能导致控制系统误判，严重时会引发灾难性后果［4-5］。状态估计能够有效减少PMU 量测信息中存在的随机误差，保证PMU 量测数据的可靠性［6-7］。因此，研究基于PMU 的机电暂态过程动态状态估计至关重要。

当系统经历较大扰动时，系统拓扑变化且难以实时获取，传统静态状态估计方法不再适用。发电机转子动态过程相对缓慢，其状态量不会突变［8］，同时在扰动下关注焦点亦从潮流分布转向功角稳定性，所以在机电暂态动态状态估计中，估计状态量从系统的静态状态量（节点电压幅值、相角）转向动态状态量（发电机功角与转速）。因此，需要进行发电机动态状态估计。

相关学者围绕发电机动态状态估计问题开展了广泛研究。文献［9］基于发电机二阶动态方程建立了线性动态状态估计模型，并采用卡尔曼滤波进行求解，但其忽略了发电机模型的非线性特征。文献［10］采用扩展卡尔曼滤波（extended Kalman filter，EKF）进行估计，但因为EKF 存在较大截断误差，对于强非线性系统估计精度较差。文献［11］提出改进EKF，利用插值法在连续采样点间增加伪量测以减小截断误差。文献［12-13］改变了非线性模型线性化的思路，基于采样点变换提出了无迹卡尔曼滤波（unscented Kalman filter，UKF）动态状态估计，提高了估计精度，但UKF 需要选择滤波参数值，灵活性不佳。文献［14］利用容积卡尔曼滤波（cubature Kalman filter，CKF）对发电机动态状态进行跟踪，CKF 无须选择任何参数，算法灵活度和精度更高。

在电力系统实际运行中，PMU 量测会出现不良数据，上述方法未考虑不良数据对状态估计结果的影响。文献［15］利用残差检测量测中的不良数据，通过迭代排除的方式辨识出存在不良数据的量测量。文献［16］提出一种基于鲁棒容积卡尔曼滤波（robust cubature Kalman filter，RCKF）的发电机动态状态估计方法，通过在算法中引入噪声尺度因子，抑制量测不良数据的影响，但上述方法未考虑同样由PMU 量测得到的估计器输入量也有可能存在不良数据的问题。文献［17］在PMU 输入量测和输出量测不同时出现不良数据的前提下，利用新息分别检测两者中的不良数据，但输入和输出量测都来自发电机出口的PMU 数据，同时存在不良数据的情况很有可能发生［18］。

针对上述问题，本文提出了一种改进容积卡尔曼滤波（improved cubature Kalman filter，ICKF）方法。首先，分析了输入量不良数据对发电机动态状态估计的影响。然后，基于历史数据利用指数平滑方法对当前时刻进行状态预报，再将该预报值与发电机模型预报值相比较，以检测输入量中的不良数据。当检测到不良数据时，基于指数平滑预报值和最小二乘法对输入量进行校正。算例结果表明，该方法能有效抑制输入量中的不良数据对发电机动态状态估计的影响。

1 发电机模型及输入不良数据影响分析

1.1 同步发电机模型和量测方程

发电机动态状态估计模型包括状态方程和量测方程两部分。状态方程选择发电机四阶模型［19］，如式（1）所示。

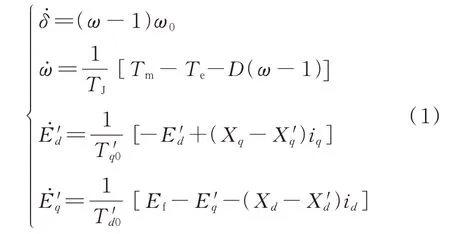
式中：δ 为发电机功角；ω 和ω0分别为电角速度和同步转速；TJ为惯性时间常数；Tm和Te分别为发电机输入机械转矩和输出电磁转矩；D 为阻尼系数；E＇d和E＇q分别为d 轴和q 轴暂态电动势；Ef为励磁电动势；T＇d0和T＇q0分别为d 轴和q 轴开路暂态时间常数；Xd和X＇d分别为d 轴同步电抗和暂态电抗；Xq和X＇q分别为q 轴同步电抗和暂态电抗；id和iq分别为d 轴和q 轴定子电流。

对于量测方程，结合发电机状态估计方程的能观性需求以及中国PMU 特有的发电机内电势量测功能，选择发电机功角δ、转子角速度ω 和发电机输出有功功率Pe作为量测量。量测方程如（2）所示。

式中：ud和uq分别为发电机d、q 轴定子电压；下标z表示PMU 量测。

式（1）和式（2）中的id、iq、Te、ud和uq可进一步表示为：

式中：U 和φ 分别为发电机出口电压相量幅值和相角，由PMU 量测得到。

由发电机动态方程和量测方程可得到状态向量x、系统输入向量u 和量测向量z：

上述发电机状态估计模型属于连续时间的动态系统，然而PMU 量测数据属于离散采样，且状态估计和控制算法经常在数字电路中实现，这就需要把连续时间的动态系统转化为离散形式［20］。将上述状态估计模型用一般状态空间模型可表示为：

式中：下标k 表示k 时刻对应变量的值；Δh 为采样间隔。

则式（7）所示的连续时间系统可用如下离散形式表示：

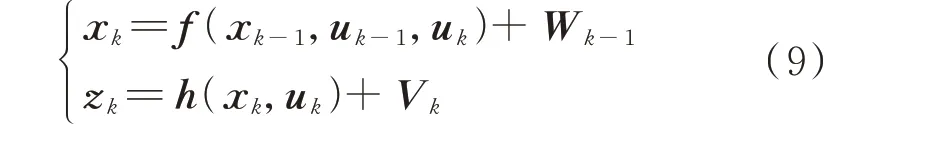
式中：f 和h 分别表示向量值非线性函数fc(·)和hc(·)的离散形式。

1.2 输入存在不良数据的影响分析

式中：R 为量测误差协方差矩阵。

由式（16）和式（17）可知，在计算量测量预报值时也需要当前时刻输入uk的值，若其存在不良数据，则会造成量测量预报值zk|k-1不准确，最终影响状态估计结果的准确性。

综上所述，输入存在不良数据会使状态预报值和量测量预报值存在较大偏差，致使最终状态估计结果不正确。此外，对于基于新息Ek的量测不良数据处理方法，当输入不正确而量测量正常时，Ek也会变大，最终导致对正常量测值的误判。

2 基于ICKF 的发电机动态状态估计

针对发电机机端电压相量U̇和量测向量z 由PMU 量测得来，可能会产生不良数据的问题，本章结合发电机状态量不突变的特点，基于指数平滑方法检测输入u 中的不良数据，并利用最小二乘法加以校正。

2.1 基于指数平滑预报的不良数据检测方法

2.1.1 基于指数平滑法的状态量预报

指数平滑法用于对时间序列的预测，是一种特殊的加权平均法。通过对本期观测值和本期预测值赋予不同的权重，求得下一期预测值，其特点在于给过去的观测值不一样的权重，即较近期观测值的权数比较远期观测值的权数要大［22］。

由式（12）可知，若当前时刻k 的输入量uk存在不良数据，会使xk|k-1存在较大偏差；而发电机的状态量受动态方程约束不突变，且与历史时刻的状态值有关，所以可采用指数平滑方法进行状态预报。

指数平滑法可分为1、2、3 次指数平滑，分别适用于无趋势、线性和2 次时间序列。根据发电机状态变量的变化趋势，选择3 次指数平滑作为本文的预报方法。将k 时刻之前T 个时刻的发电机状态估计值x̂k-T，x̂k-T+1，…，x̂k-1作为观测值输入指数平滑算法，可得到k 时刻的状态预报值x＇k|k-1。首先计算3 次指数平滑值：

然后利用k-1 时刻的3 次指数平滑值对k 时刻状态值进行预报：

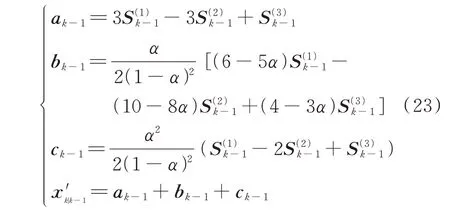
式中：ak-1、bk-1、ck-1为线性平滑参数；x＇k|k-1为k 时刻指数平滑预报值。

平滑参数α 的大小代表近期数据的权重，取值在［0，1］之间，当α 改变较小时，其预测效果变化不大。故本文将区间［0，1］十等分，然后在每个区间内以式（24）各个状态量相对误差均方根和（sum of root mean square error，SRMSE）S 最小作为目标，采用0.618 法［23］对α 进行搜寻，0.618 法的详细步骤见附录A，最后取10 个区间中SRMSE 最小的α 作为最终的平滑参数。

当输入uk正常时，ek较小；而当输入中存在不良数据时，xk|k-1会产生较大偏差，而x＇k|k-1只跟历史时刻状态估计值有关，不受发电机模型和输入量影响，故两者差值ek就会明显变大。这一点会在后续仿真中验证。

为了对ek的大小进行分析，以确定输入中是否存在不良数据，需要给出一个比较基准。考虑到正常情况下ek较小，且稳定在某个范围内，选择历史时刻ek的平均值作为判断基准，计算方法如下：

得到emean之后，就可以通过比较ek与emean来进行判断，具体判断方法如下，首先定义N：

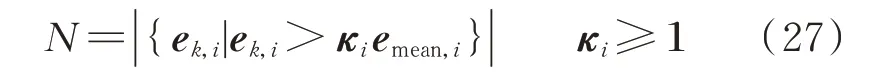
式中：下标i=1，2，3，4 表示为向量的第i 个元素；N为集合元素个数；κi为κ 的第i 个元素，是为了降低误判概率而对每个状态变量设置的裕度系数。

一般认为误差大于3σ 的量测数据为不良数据，其中σ 为量测误差标准差，根据PMU 量测标准［24］，将量测误差为3σ 的电压相量量测数据输入ICKF中，得到此情况下ek与emean的比值，经过多次测试后取平均后取整得到κref=［1，2，4，5］，作为κi取值的参考。考虑到3σ 准则是静态情形下常用的不良数据判别准则，而动态过程中量测误差来源更为复杂，所以在κref基础上适当提高κ 以减少误判。此外，由式（1）和κref可知，发电机功角只与角速度有关，输入uk是否存在不良数据对功角预报值都无影响，故κ1应设为较大数值以消除其对N 的影响，κ 的最终取值在3.1 节中给出。

为了提高灵敏度，认为当N ≥2 时，即有2 个状态变量满足ek，i＞κiemean，i时，输入uk存在不良数据。当k 时刻判断出不良数据，需要将ek置0，否则因为其值较大，会影响后续时刻emean的计算，而ek为0 又会导致后续emean的计算结果较正常值偏低，容易导致误判，所以在计算emean时要用不为零的差值绝对值向量。

2.2 基于最小二乘法的输入不良数据校正

在检测到输入uk存在不良数据后，用x＇k|k-1代替xk|k-1参与下一步计算。而存在不良数据的输入uk仍未进行处理，其仍会通过式（16）影响动态状态估计结果，所以本节基于最小二乘法［25］来校正输入uk。

使用二阶Runge-Kutta 方法离散化后的动态状态估计预报方程如下：

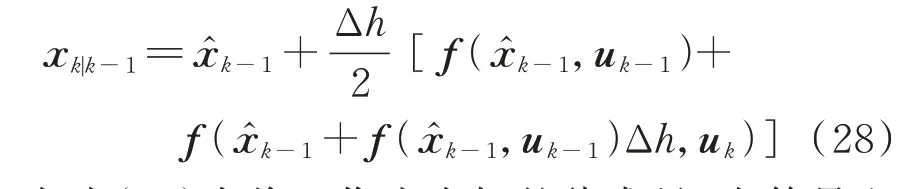
在式（28）中将uk作为未知的待求量，在等号左边用指数模型预报值x＇k|k-1代替xk|k-1，其余变量x̂k-1和uk-1是已知的，则该问题转化为一个典型的静态估计问题：

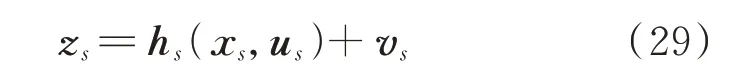
式中：下标s 用于和发电机量测方程作区分，vs一般表示量测噪声，在此处表示x＇k|k-1与真实值的误差。

式（28）等号右侧为hs(·)的具体表达形式，x＇k|k-1为量测量zs，uk为待估计状态量xs，输入量us=［x̂k-1，uk-1］，则可利用最小二乘法求解uk，其步骤如下所示：

式中：J 为hs对xs的雅可比矩阵；ε 为迭代误差；上标i表示第i 次迭代。当ε 小于给定值时，停止迭代，输出uk的估计值。

2.3 ICKF 方法实施步骤

为方便实施，下面给出基于ICKF 方法的发电机动态状态估计具体步骤和流程图，如图1 所示。

图1 ICKF 方法流程图Fig.1 Flow chart of ICKF method

1）初始化

步骤1：设定初始时刻状态值x̂0和状态估计误差协方差矩阵P0，初始输入u0取为稳态运行值，设定过程和量测噪声协方差矩阵R 和Q。

2）预报步

步骤2：利用式（10）至式（14）计算k 时刻的状态预报值xk|k-1及其协方差矩阵Pk|k-1。

步骤4：通过式（25）至式（27）判断输入uk是否存在不良数据，若检测到不良数据，用x＇k|k-1替换xk|k-1，将ek设置为0，转至步骤5；若无不良数据，直接转至步骤6。

步骤5：设置迭代精度ε，通过式（28）至式（32）估计输入uk中的发电机机端电压相量。

3）滤波步

步骤6：利用式（15）至式（21）以及x＇k|k-1和校正后的输入uk进行滤波，计算得到k 时刻状态估计值x̂k和估计误差协方差矩阵Pk。令k=k+1，返回步骤2，进行下一次迭代。

3 算例分析

3.1 仿真设置

基于IEEE 39 节点系统对所提方法进行验证分析，该系统的拓扑结构在附录B 给出。

选取节点36 所连发电机G6 作为研究对象。线路17-27 发生三相金属性短路，故障持续0.1 s 后清除，采样间隔为0.02 s，仿真时间为20 s。将由BPA时域仿真获取的故障后电气量作为真实值，在真实值基础上添加噪声作为量测，过程和量测噪声的协方差矩阵Q 和R 分别设定为10-6In和10-6Im，其中In和Im为单位矩阵。本文所提ICKF 算法相关参数中，α 经0.618 法搜寻后设为0.589，考虑降低误判概率κ 设为［10，3，5，6］，最小二乘法迭代精度ε 设为10-6。以上参数的设置方法已在前文给出。此外，利用仿真验证了所选参数对电网负荷水平和拓扑结构变化有较好的适应性，仿真结果见附录C。

3.2 指数平滑预报方法的准确性评价

正常情况下，即无不良数据时，发电机模型预报值和指数平滑预报值的差值（ek）如图2 所示。由图2 可以看出，正常情况下模型预报和指数平滑预报值相差较小，且在整个估计过程中，两者差值大小较稳定，这一点有利于利用两者差值检测输入中的不良数据。

图2 正常情况下2 种预报值差值比较Fig.2 Difference comparison between two kinds of predicted values in normal situation

为定量评价指数平滑预报方法的准确性，将指数平滑预报值和模型预报值与相应时刻状态变量的真实值进行比较，定义相对误差均值ε1和最大值ε2（功角为绝对误差）这2 个评价指标，其表达式为：

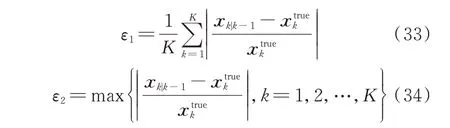
式中：K 为采样点总个数；xtruek为状态变量真实值。

2 种预报值的ε1和ε2如表1 所示。由表1 可知，2 种预报方法的相对误差较接近，说明指数平滑预报提供的预报值较为准确，可以用于状态估计的后续步骤。

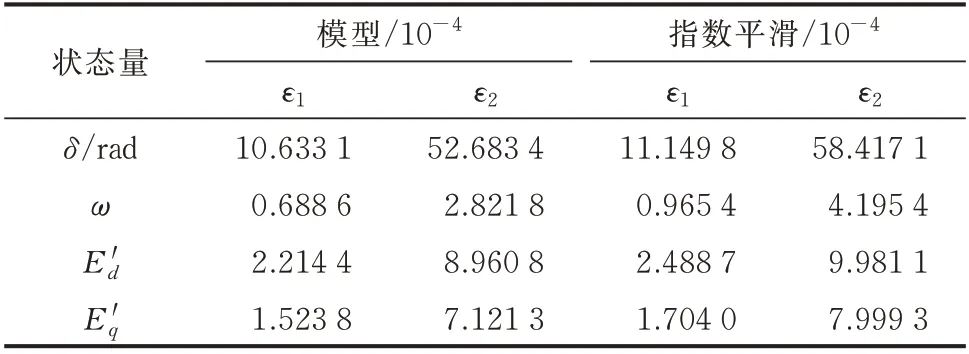
表1 2 种预报值误差比较Table 1 Error comparison between two kinds of predicted values

在4.0～4.2 s，对输入电压幅值加入量测值10%大小的随机偏差，对输入电压相角加入0.03 rad 的误差，以测试输入量存在不良数据时指数平滑预报方法的准确性。此种情况下发电机模型预报值和指数平滑预报值的差值（ek）如图3 所示。

图3 给出了有不良数据存在的情况下，模型预报值和指数平滑预报值的差值随时间变化的情况。可以看出，在4～4.2 s，两者的功角预报差值变化不大，由前述分析可知，发电机功角只与角速度有关，输入uk是否存在不良数据对功角预报值都无影响，这一点在此得到证实；而对于另外3 个发电机状态量，两者的差值明显变大，这是由于指数预报值只跟历史时刻的状态估计值有关，不受输入量的影响，而模型预报值则不然，所以差值ek可以作为判断输入存在不良数据的依据。

图3 输入存在不良数据情况下2 种预报值差值比较Fig.3 Difference comparison between two kinds of predicted values with bad data in input

3.3 输入存在不良数据时的估计结果对比

为测试所提方法对输入不良数据的鲁棒性，在仿真中加入与3.2 节相同的输入不良数据，并选择文献［17］所提方法作为对比算法1，估计结果如图4所示。

图4 给出了在输入存在不良数据的情况下，CKF、本文ICKF 以及对比算法1 的估计结果。由图4 可以看出，在4.0～4.2 s，由于输入存在不良数据，CKF 的估计结果出现较大偏差，此影响不只存在于4.0～4.2 s，还会影响后续一段时间的估计结果。ICKF 和对比算法1 由于能够检测并校正输入中的不良数据，估计结果与真实值基本吻合。对比算法1 利用新息Ek来检测输入不良数据，但计算Ek时会用到量测数据，当量测值也存在不良数据时就会造成检测失败，影响估计结果。相比之下，ICKF 利用指数平滑预报值进行输入不良数据的检测和校正，不受量测值的影响。

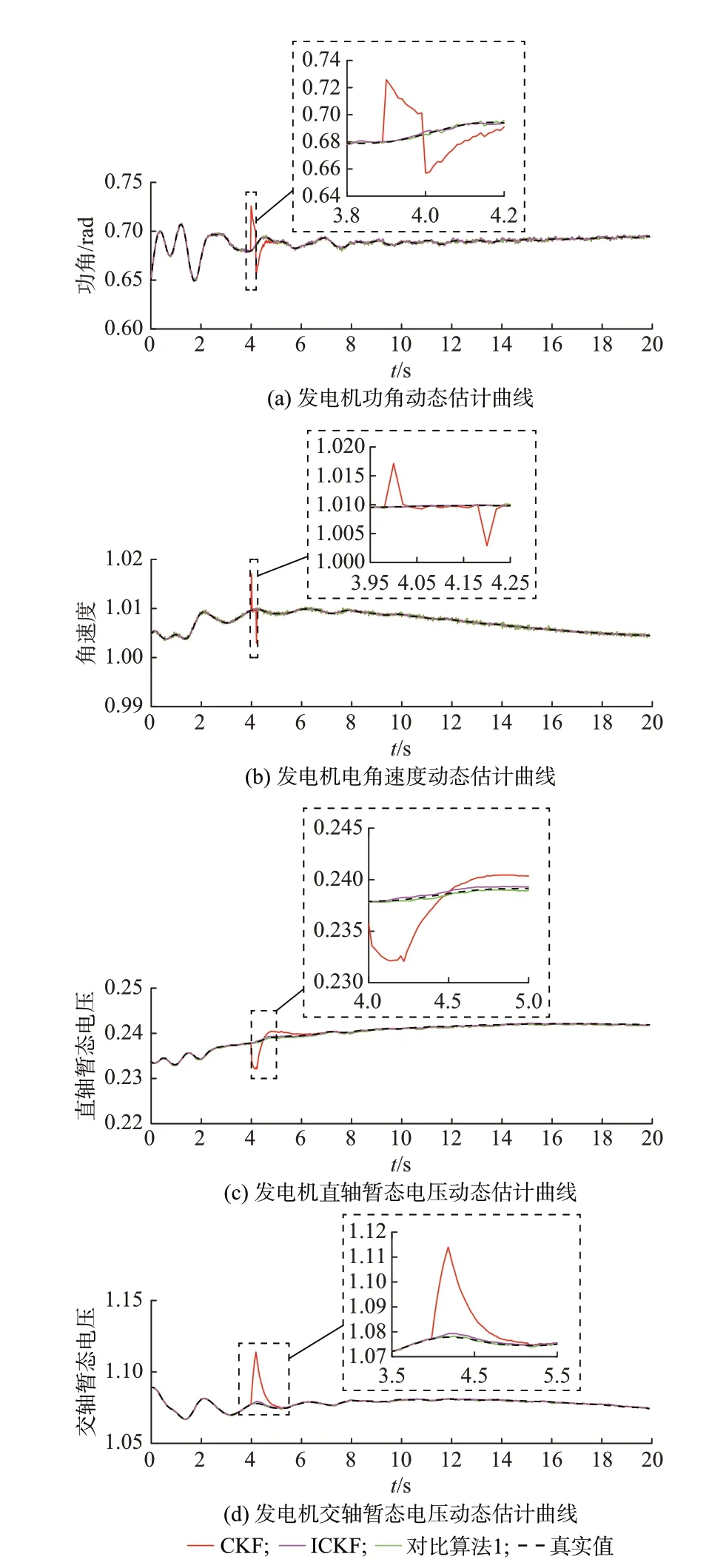
图4 输入存在不良数据时动态状态估计结果Fig.4 Dynamic state estimation results with bad data in input

为定量评价所提方法的有效性，定义相对估计误差平均值ε3：

表2 输入存在不良数据时估计结果定量比较Table 2 Quantitative comparison of estimated results with bad data in input

为了验证ICKF 方法对输入不良数据的校正效果，表3 给出了4.0～4.2 s 输入电压相量在校正前后与真实值的误差，其中幅值为相对误差，相角为绝对误差。

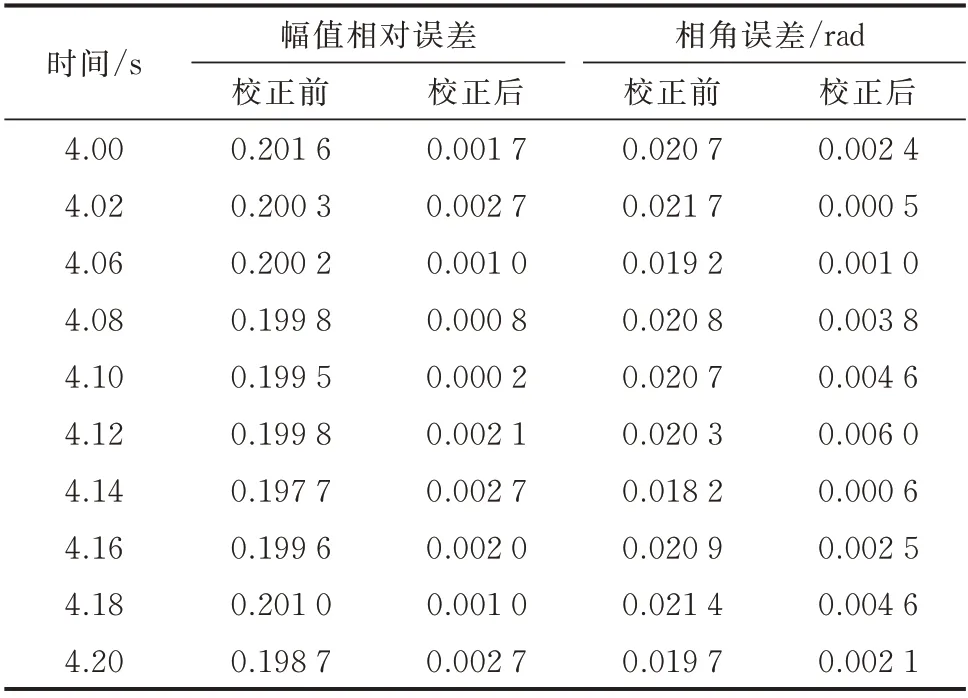
表3 输入校正结果Table 3 Input correction results

从表3 可以看出，ICKF 能够准确检测输入不良数据并且校正。经过校正，输入电压相量误差明显减小，可用于卡尔曼滤波器的后续步骤。

3.4 对基于新息的量测不良数据处理方法的改进

对于基于新息的量测不良数据处理方法，当输入不正确而量测量正常时，新息Ek也会变大，可能导致对正常量测值的误判。为解决这一问题，将本文所提方法与文献［16］中所提RCKF 方法结合为改进鲁棒容积卡尔曼滤波方法（improved robust cubature Kalman filter，IRCKF），并进行仿真测试。

选择文献［15］所提方法作为对比算法2。在4.0～4.1 s，对发电机输出的有功功率Pe添加其量测值10% 大小的随机误差，以测试CKF、RCKF、IRCKF、对比算法1 以及对比算法2 这5 种方法对量测不良数据的鲁棒性；在8.0～8.2 s，除量测Pe添加不良数据，对输入电压相量加入与3.2 节相同的不良数据，测试5 种方法能否处理输入与量测同时存在不良数据的情况。5 种方法的估计结果如图5所示。

由图5 可知，在4.0～4.1 s，由于有功量测存在不良数据，CKF 估计结果产生较大偏差，而其他4 种方法能够滤除量测不良数据的影响；在8.0～8.2 s，当输入和量测同时存在不良数据时，只有IRCKF 能够基于指数平滑预报方法处理输入不良数据，估计结果与真实值基本吻合，其他4 种方法的估计结果都出现了较大偏差。对比算法1 利用新息的异常来检测不良数据，无法处理输入和量测同时存在不良数据的情况。对比算法2 和RCKF 无法处理输入不良数据。

图5 输入和量测存在不良数据时状态估计结果Fig.5 State estimation results with bad data both in input and measurement

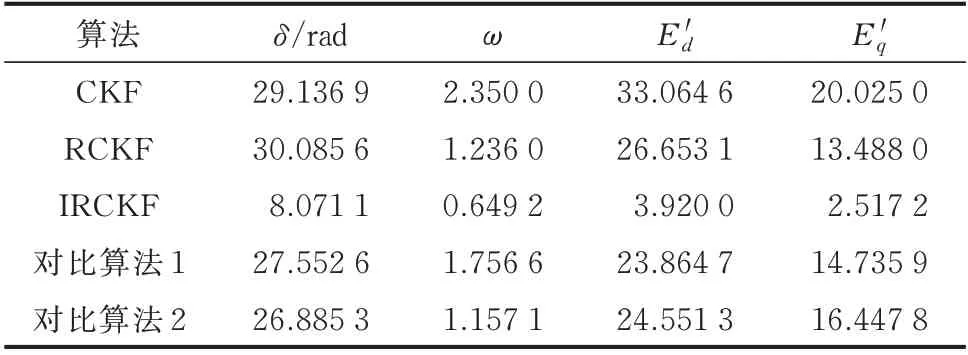
表4 输入和量测存在不良数据时估计结果定量比较Table 4 Quantitative comparison of estimated results with bad data both in input and measurement

4 结语

针对发电机动态状态估计中输入量有可能存在不良数据的问题，本文提出了一种基于ICKF 的发电机动态状态估计新方法。通过指数平滑方法预报状态量，并与发电机模型的预报值相比较，利用指数平滑值不受输入影响的特性抑制输入中的不良数据，最后利用最小二乘法校正不良数据。仿真测试表明，输入存在不良数据时，该方法能够准确估计状态量，且能与基于新息的量测不良数据处理方法相结合，同时处理这2 种不良数据。

本文不足之处在于所用指数平滑预报方法较简单，且涉及参数选取的问题，今后考虑利用人工智能相关方法进行时间序列预测和参数选择，进一步提升算法的鲁棒性。此外，后续将考虑采用数学工具对所提方法进行理论分析与证明。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。