例谈含参绝对值函数最值问题的求解策略

翁建良

摘 要：本文针对易错例题进行剖析，采用变式法、数行结合法谈含参绝对值函数最值问题的求解策略.

关键词：绝对值;最值问题;数形结合

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2022）04-0006-03

1 例题——“单绝单参双最”

例题 函数f（x）=x+4x-a（a∈R），当x∈[1，3]时，记f（x）的最大值为M（a），则M（a）的最小值为.

解法1 （换元法和图象法）令t=x+1x∈2，103，则原函数转化为g（t）=t-a，其中t∈2，103.

所以M（a）=max2-a，103-a.

在同一坐标系中画出函数y=|2-a|和y=|103-a|的图象，则M（a）表示的即为两函数图象上边界部分.

于是当a-2=103-a，即a=83时，M（a）的最小值为23.

解法2 （利用绝对值三角不等式）

因为M（a）=max2-a，103-a，

所以可得M（a）≥|2-a|，M（a）≥|103-a|.

则2M（a）≥|2-a|+|103-a|

≥|2-a-（103-a）|=43.

所以M（a）≥23，当且仅当a=83时取到等号，即M（a）的最小值为23.

解法3 （几何法——数形结合）

f（x）可理解为函数y=x+1x上的点与直线y=a的纵向距离，这样我们就将问题转化为两个函数图象纵向距离的最大值的最小值.

故f（x）的最大值M（a）=max{|2-a|，|103-a|}.所以M（a）min=103-22=23.

此时y=a=103+22=83.

评析 解法3利用数形结合思想将整个题目的难度降低，也将看似很难的题目变得简单而又通俗易懂.如果将定义域改为x∈[12，3]，用解法3，结合图象分析，可以发现M（a）的最小值只与函数y=x+1x的最高点和最低点有关，与端点无关.

2 拓展1——“单绝双参双最”变式1 函数f（x）=x+1x-ax-b（a∈R，b∈R），当x∈[12，2]时，记f（x）的最大值为M（a，b），则M（a，b）的最小值为.

分析 首先f（x）可理解为函数y=x+1x上的点与直线y=ax+b的纵向距离.

记M（a，b）=M，則x+1x-ax-b≤M.

即ax+b-M≤x+1x≤ax+b+M.

所以函数y=x+1x图象夹在两条平行线y=ax+b-M与y=ax+b+M之间，如图1所示.

当两条平行线间的纵向距离最小时，M（a，b）取到最小值，当M（a，b）取到最小值时，y=x+1x恰好夹在两条平行线（图中的两条实线）y=52与y=2之间，如图2所示.

此时直线（图中的虚线）y=ax+b=52+22=94，此时a=0，b=94.

所以M（a，b）min=52-22=14.

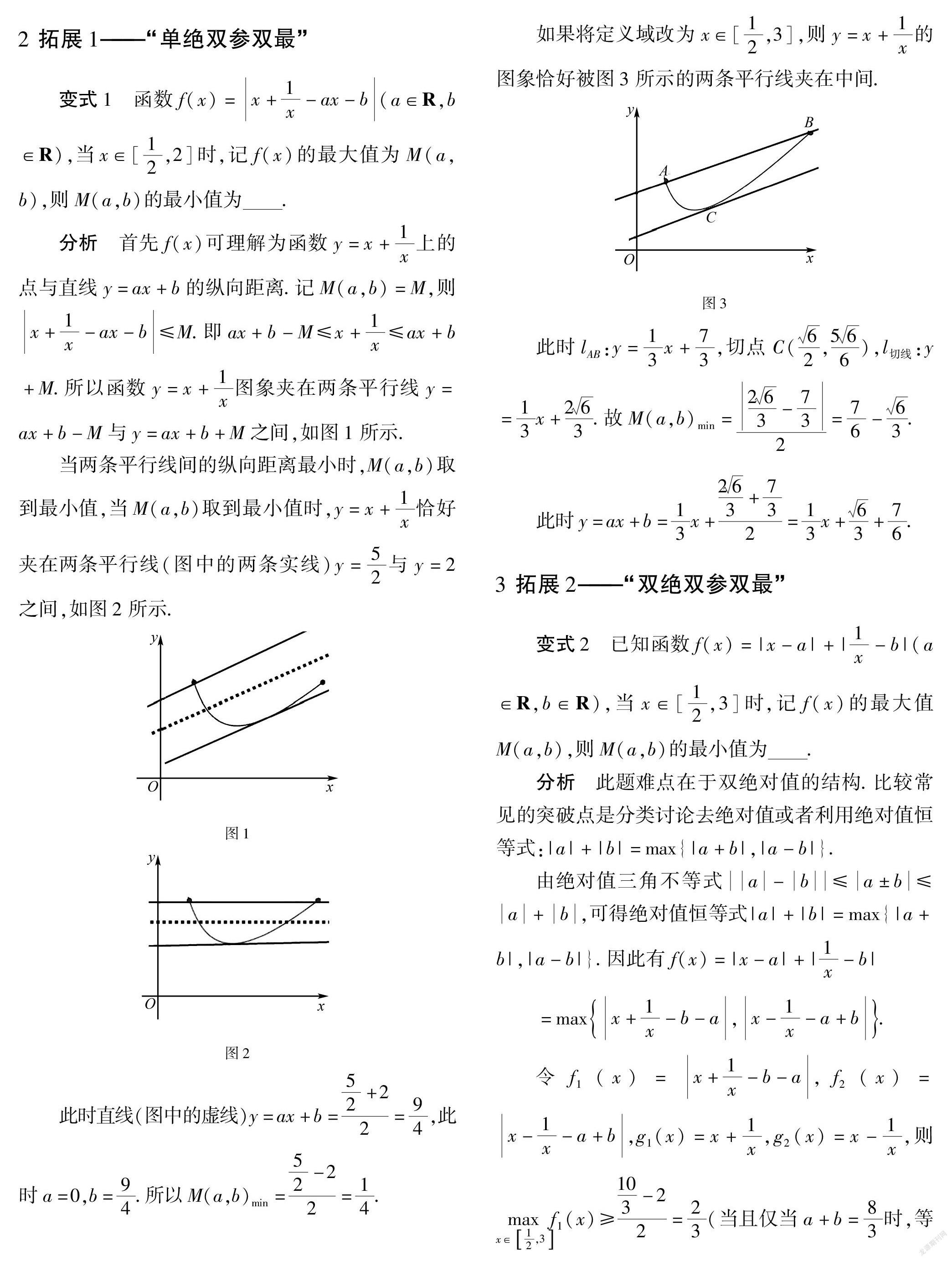
如果将定义域改为x∈[12，3]，则y=x+1x的图象恰好被图3所示的两条平行线夹在中间.图3

此时lAB：y=13x+73，切点C（62，566），l切线：y=13x+263.故M（a，b）min=263-732=76-63.

此时y=ax+b=13x+263+732=13x+63+76.

3 拓展2——“双绝双参双最”

变式2 已知函数f（x）=|x-a|+|1x-b|（a∈R，b∈R），当x∈[12，3]时，记f（x）的最大值M（a，b），则M（a，b）的最小值为.

分析 此题难点在于双绝对值的结构.比较常见的突破点是分类讨论去绝对值或者利用绝对值恒等式：|a|+|b|=max{|a+b|，|a-b|}.

由绝对值三角不等式a-b≤a±b≤a+b，可得绝对值恒等式|a|+|b|=max{|a+b|，|a-b|}.

因此有f（x）=|x-a|+|1x-b|

=maxx+1x-b-a，x-1x-a+b.

令f1（x）=x+1x-b-a，f2（x）=x-1x-a+b，g1（x）=x+1x，g2（x）=x-1x，则maxx∈12，3f1（x）≥103-22=23（当且仅当a+b=83时，等号成立），

maxx∈12，3f2（x）≥83-（-32）2=2512（当且仅当a-b=712时，等号成立）.

因此M（a，b）min=2512（当且仅当a-b=712时，取到最小值）.

评析 此题利用绝对值恒等式将两个绝对值的问题转变为一个绝对值的形式，从而把该问题转化为例题的结构.

笔者通过对一道典型例题及其变式的研究，提炼出一类含参数双绝对值最值问题的一般解法，即先利用绝对值恒等式将双绝对值转化为单绝对值，再利用数形结合将代数问题转化为几何问题，实现复杂问题简单化，抽象问题直观化，代数问题几何化，从而揭示问题本质，将难度较大的问题降维，完成一题多解到多题一解的跨越.

参考文献：

[1] 李文东.已知函数的最值求参数的值或范围问题的求解策略[J].数理化解题研究，2021（16）：34-35.

[2] 吕相红.高中函数“最值”问题的求解策略[J].中学生数理化（教与学），2020（09）：90.

[责任编辑：李 璟]