万变不离本质 殊途终须同归

潘吉丽

[摘 要] 在数学教学中，数学问题千变万化错综复杂，其实很多问题，只要我们抓住图形的几何特征，探索图形变化过程中的变与不变，挖掘问题内涵本质，提炼其解题规律及思想方法，就可以将问题迎刃而解.

[关键词] 线段；最值问题；应用

笔者对《宁波市2016年初中毕业生学业考试说明》中利用“圆外一点到圆上点的最大距离和最小距离”模型求线段最值问题的应用进行了初浅分析和研究，这类问题起点高，将多个几何图形融合在一起，学生无从下手，总找不到合适的处理方法，那么如何解决这类问题呢？我们发现解决如此难的问题，只要掌握分析问题和解决问题的一些基本方法和技巧，充分利用已知条件，渗透转化思想，可将这些最值问题最终转化为同一相应的数学模型进行求解.

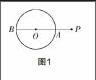
模型：如图1所示，点P为⊙O外一点，则点P到⊙O上各点距离的最大值为线段PB的长，最小值为PA的长（直线PB经过圆心O）.

无中生圆用模型

例1： 如图2所示，在等腰直角三角形ABC中，AB=BC=2，点P为等腰直角三角形ABC所在平面内一点，且满足PA⊥PB，则PC的取值范围是______.

分析：本题变化的量比较多，不变的是∠AOD=30°和AB=3，因为AB=3为定值，AB所对的张角∠AOD=30°是个定角，所以可将点O看成△OAB的外接圆⊙O′上的动点，要求CO的最大值可转化到“圆外一点到圆上点的最小距离和最大距离”模型来求解. 如图5，过点A，O，B三点作辅助圆⊙O′，因为∠AOD=30°，所以∠AO′B=60°，可知△ABO′为等边三角形. 易证四边形O′ACB为菱形，因此O′C=3，OO′=3. 故OC的最大值就是O′C+OO′，从而可求出点C到原点O的最大值为3+3.

解题就要抓住问题的本质及关键点，例1中有直角，根据“直径所对的圆周角是直角”，由直角可直接联想到作辅助圆，即点P的运动轨迹是一个圆；例2中有定角和定线段，根据“圆中相等的圆周角所对的弦相等”可将点O看成△OAB外接圆⊙O′上的动点. 数学的一个最大魅力就是知识间的互相渗透和运用，这两道例题使我们充分感受到了辅助圆的巨大作用. 作出辅助圆后可以利用“圆外一点到圆上的点的最小距离和最大距离”模型求解. 巧妙地构造辅助圆是灵活运用数学模型解决问题的关键，我们必须抓住问题本质条件，掌握解题方法，这样才能很快把问题化繁为简、化难为易.

构造相似套模型

随着问题的层层深入，例3、例4难度又进了一步，此两题条件中变化的量多，动静结合，不光是直接利用模型求解，还要我们观察、发现、分析数学模型，不流于形式，而此时例3、例4解题的重心放在了利用构造相似方法转化到求线段的最小值，即先通过相似三角形的对应边成比例转化到求线段的最小值，再利用模型“圆外一点到圆上点的最小距离和最大距离”求出线段的最小值，此过程让我们充分体会基本问题知识的类比与迁移，由现象到本质地加以引導，始终想办法如何运用已知条件把要求线段的最值问题转化为相应的数学模型来求解.

转化思想归模型

例5：如图10所示，点P的坐标为（3，4），⊙P的半径为2，A（2.8，0），B（5.6，0），点M是⊙P上的动点，点C是MB的中点，则AC的最小值是______.

例5的解题重心放在了数学转化的思想上，A（2.8，0），B（5.6，0）隐含了中点条件. 通过三角形中位线策略转化到要求的线段AC的最小值，体现了数学的转化思想，揭示了数学的本质，在运用模型的过程中并注意与之相伴的“数学思想方法”的渗透. 我们应充分挖掘问题的本质条件，使原来较为抽象、隐含的条件清晰地显现出来，让如此复杂的题目变得如此简单，达到事半功倍的效果. 尽管题目灵活多变，但始终不变的是如何创造条件灵活地运用模型，并运用数学转化思想把要解决的问题化归到相应的数学模型，即解决问题的本质方法不变.

总之，授人以鱼，不如授人以渔，在数学教学中，要与学生共同探讨基本问题模型与解题的联系，还原知识的发生、发展及形成过程，使学生对数学中隐含的本质有深刻的理解. 恰当地运用数学模型方法，可以将纷繁复杂的问题化归为我们熟悉的数学模型进行求解. 不论题目如何变化，只要我们抓住了解决问题的本质方法，便所有作法都相同. 真所谓题目万变，最终解决问题的方法却殊途同归.