浅谈初中数学“几何例题”的变式教学

苏志朝

【摘要】初中数学几何题，对于教师和学生来说都有一定的抽象性。特别是在农村初中，学生对几何知识的掌握程度不够，想象力有一定限制，对难度大、证明步骤复杂的例题，学生难以理解，面对简单的几何例题，学生的思考深度又不够，从而导致学生对学习数学的兴趣不高，甚至对几何的一些题目都恐惧。因此，教师如何在课堂中实施几何例题变式教学变得尤为重要，文章以初中“图形平移与旋转”一例题设计为例，探讨变式教学在例题教学中的重要性。

【关键词】初中数学;几何例题;变式教学

数学作为一门基础性学科，是人们对客观世界定性把握和定量刻画、逐渐抽象概括、形成方法和理论，并进行广泛应用的过程。教师在教学过程中，要考虑数学自身的特点，遵循学生学习心理规律，让学生亲身经历将实际问题抽象成数学模型并进行解释与应用。因此，把课堂中的变式教学运用到例题中，可以有效实现学生亲身经历知识的变化，培养学生的推理能力和逻辑思维能力，使学生更好地掌握知识和解题方法。初中几何例题教学是课本知识的一个范围，但教师要学生掌握的是把学到的技能融会贯通，能解决同一知识不同的问题。应用数学几何例题变式教学的方法会无形中提高教学效率。

一、精选几何例题，提高课堂教学的有效性

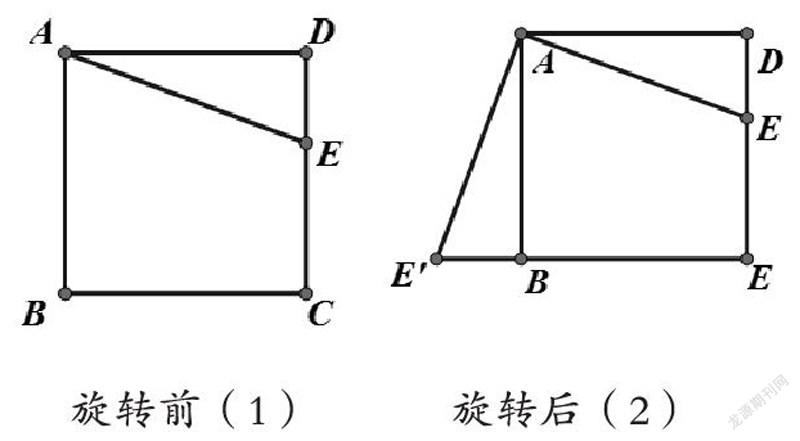
初中数学课本的例题都是经过各专家研究精选出来的，具有一定的代表性，包含着新知识的运用，难度适中，符合大部分学生的学习能力，但教师在例题教学中，要根据例题的内容和教学的知识进行适当的变式，从变式中检验学生对知识点的掌握。几何例题的变式多样化，思维发散也比较广，因此教师在选择例题的时候，要根据学生特点，从教学目标出发，围绕教学重点教学，精选出符合新授课知识的例题进行变式训练，提高学生的思维能力。例如，人教版九年级上册《图形平移与旋转》一课中，学习了旋转的性质：1.对应点到旋转中心的距离相等;2.对应点与旋转中心所连线段的夹角等于旋转角;3.旋转前后的图形全等。学生如何应用旋转的三个性质，课本就用一例题检验学生的掌握情况，教师可以通过选择这个例题检验学生的掌握情况。例：如图，E是正方形ABCD中CD边上任意一点，以点A为中心，把顺时针旋转90度，画出旋转后的图形。

这道题难度不算大，一方面考查学生对旋转性质的运用;另一方看还考察了学生的动手能力，根据性质，也很容易得道旋转后的图形。

例题的选择必须要有一定的基础性和代表性，遵循从易到难的原则。这道例题，对于很多同学都能够掌握，难度不大，但真正理解旋转的性质，教师可以根据这个例题进行题目的变式，提高学生的数学解题能力和思维能力。

二 变式教学法在课堂例题教学中的应用

1. 在讲授知识方面的应用

教材中的例题，本身就有一定的代表性，注重的都是引导学生对知识的掌握，旨在培养学生的思维能力，因此课本的例题难度适中，适合大部分学生。在教学中，教师需要的是给予学生一个平台展示，新课本指出，数学活动必须建立在学生认知发展水平和已有的知识经验基础上，激发学生积极性，向学生提供从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本数学知识和技能。学生有平台展示，才能更好地发挥例题的作用，对例题才能更加深入研究，采用不同的解题方式培养学生思维的深刻性与灵活性，那这样的教学才有价值。如刚才的例题，引导学生把习题与例题联系起来，把新知识合理运用。如题目可以变形为：

如图：点E是边长为a的正方形ABCD中CD边上任意一点，以点A为中心，把顺时针旋转90度。

（1）画出旋转后的图形;

（2）连接KE，是_______三角形，说明你的理由。

这个题目就是在原来例题的基础上进行变形，依然是把图形进行旋转，学生也根据例题的解题方法动手操作，把图形画出来，而在画旋转图形过程中，实际上已经融入旋转的性质了，学生对性质的掌握是否能够在讲授知识的时候 ，教师可以观察到，那么题目中的第二个问题，是一个什么三角形呢？从旋转的性质可以知道，旋转后的图形相等，旋转角为90度，也就是AE=AK，，可知，是一个等腰直角三角形，从而更好地体现旋转性质在题目中的运用，把例题与习题联系起来。这样的变式题有利于培养学生思维的深刻性与灵活性，拓展思维的广度和深度。

2. 在培养能力方面的应用

学生的发散思维能力需要在平时学习中不断培养，使学生达到解决问题、善于变通，因此在变式训练中对能力的培养尤为重要，包括题目的一题多解，一题多变，逐步深入，教师无论采用哪种方式，都是以基础为主，引导学生拓展思路，采用逆向、正向思考不同的问题，或者把题目逐步向深一层引导发展，促使学生不断思考，不断探索，也有利于学生对知识的掌握。如把刚才旋转的题目继续变式，加深学生对例题的理解，掌握旋转的知识，应用在实际的解题中。

如图在正方形ABCD中，，点F为BC上一点，点E为DC上一点，的两边AE、AF分别与直线BD交点M、N，连接EF：

（1）EF=BF+DE;

（2）的周长为恒值;

（3）+=。

验证以上是否成立？

这道题的难度就在原来的基础上增加了，学生如何运用旋转的性质进行验证，这就需要教师引导学生探究，发散学生的思维能力。

验证（1）的成立，EF=BF+DE，如下图所示：

不难发现≌，也可以证明≌，从而得到EF=BF+DF，证明三边关系，根据旋转相关性质，找到相应的角相等，边相等，可以得到全等三角形，也能在其中发现边与边之间的关系，无论题目如何变形，始终围绕着旋转的性质，引导学生把新学到的知识应用到练习中。

同样道理，根据旋转的性质验证（2）求的周长，也就是边与边之间的关系，如图2所示，同样可以证明≌，≌，的周长=CF+CE+EF=CF+CE+（BF+DE）=（CF+BF）=（CE+DE）=BC+DC=2a（定值），也圍绕着旋转的性质探索;

验证这两个问题后，教师可以继续引导学生加深对题目的理解，把知识点从易到难进行引导，培养学生的思维能力。

验证（3），如图三所示

（1）此题需要作辅助线，难度会增加，很多学生找不到规律，也不知道如何找三条线段之间的关系，教师可以根据+=引导，三边的关系是否像我们之前学过的勾股定理，若是勾股定理，必须三边存在同一个直角三角形中，因此采用等量代换的方法把边进行变换，转化为求证BN、BG、GN之间的关系，因此可以作AG=AM，連接BG、GN，证明≌，接着证明≌，可得NG=MN， =90度，从而得到+=，等量代换后得到+=，学生探索完三个题目，会很清楚知道，旋转的性质在解题过程中的运用，思维能力也得到很好的培养。因此，根据例题的变换，对培养学生的数学素养以及解题的能力都有很大的帮助。

三、几何题目变式，促进学生全面发展

1.几何题目变式，能培养学生的创新能力

数学有三个显著特点，这就是内容逻辑的严谨性、抽象性、应用的广泛性，它们互相联系，互相影响，密不可分。课本中有的例题对于学习能力较好的学生很容易理解，也会觉得难度比较低，有时候会对这些简单的题目失去兴趣，而有的题目相对难，学生又没有克服难题的信心，容易失去对学习数学的兴趣。因此，教师在教学中适当把例题变式，由浅入深，诱惑学生一步一步进入探究的意境，从一个知识点联系到另外一个知识点，层层探究，逐步深入，引导学生运用不同的方法进行解题，培养学生的创新能力，激发学生求知欲，提高学生学习兴趣。

2.几何解法变式，能快速培养学生的思维能力

初中数学几何题目，教师可以引导学生一题多解，采用不同的方式验证某一结论，或者用不同的方式解答问题，开动脑筋寻找更多的解题方案。帮助学生找到数学知识之间的联系，帮助学生增加数学思考的深度和广度，培养学生数学解题素养，激发学生参与课堂的积极性。在几何例题教学中，教师可以让学生初步探究一例题，寻找例题中的知识点，适当把例题变式，围绕同一个知识点思考不同的问题，可以快速培养学生的思维能力。如前面列举的例题，经过几次的变形，都围绕着旋转的性质解答问题，从不同的问题寻找不同的解决方法，加深对知识点的认识，熟练运用所学的知识。

在运用变式教学法的过程中，教师应根据例题的特点，结合知识点和学生的掌握程度把例题进行变式，不要脱离实际，过份把难度增加，违背学生的认知规律，通过思考得不到想要的结果，会降低学生的学习积极性，难以取得有效的教学效果。更应该数学知识点之间的联系，根据实际，把知识点串联起来，让学生在解决问题的时候找到规律，举一反三，形成完善的解题格局，融会贯通，活学活用。

参考文献：

[1]陈锦秀.变式教学的实践与反思：以初中数学为例[J].教育教学论坛， 2020（09）.

[2]汪景平，胡艳.逐层推进破难点 变式拓展促思维[J].中学数学教学参考，2020（35）.

[3]杨晓敏.一道立体几何题的变式探究与备考建议[J].中学数学教学参考，2020（36）.