一道高考题引发的思考
董双双
(常平中学,广东 东莞 523000)
涉及构造函数的题目在近几年的数学高考中反复出现,是一个常考点.这种类型的题目经常和导数、函数的单调性、比较大小、不等式问题等结合起来,对学生的综合能力要求较高.要解决这类问题,首先要掌握常见的构造函数的方法,学会举一反三,灵活变通,然后借助常用的数学方法,对构造出来的函数进行研究讨论,最后达到解决问题的目的.
1 试题引入
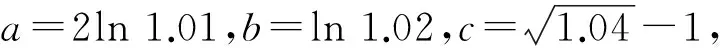
( )
A.a C.b (2021年全国数学高考卷Ⅰ理科试题第12题) 函数与方程、转化与化归是高中数学思想中重要的两大思想方法,而构造函数的解题思路恰好是这两种思想方法的良好表现.本题处于整卷的第12题,在选择题的压轴位置,难度较大.通过观察不难发现:a和b是底数相同的对数式,易于比较大小,难点在于a与c、b与c的比较.如果能够巧妙地构造一个函数,并通过函数的单调性解决问题,那么本题就简单很多.在高考中,要想在短时间内既快又准地构造出合适的函数,并且能通过导数研究出函数的单调性,对学生来说,难度较大. 解因为a=2ln 1.01=ln 1.012=ln(1+0.01)2 =ln(1+2×0.01+0.012)>ln 1.02=b, 所以b f(0)=0, 因为1+4x-(1+x)2=2x-x2=x(2-x),所以当0 1+4x-(1+x)2>0, 即 从而 f′(x)>0, 于是f(x)在[0,2]上单调递增,故 f(0.01)>f(0)=0, 即 亦即 a>c. g(0)=0, 由于1+4x-(1+2x)2=-4x2,当x>0时, 1+4x-(1+2x)2<0, 从而g′(x)<0,即函数g(x)在[0,+∞)上单调递减,因此 g(0.01) 即 亦即 b 综上所述,b 评注利用对数的运算和对数函数的单调性不难对a,b的大小做出判定,对于同上的大小关系,可以将0.01换成x,分别构造函数 利用导数分析其在0的右侧包括0.01的较小范围内的单调性,结合f(0)=0,g(0)=0即可得出a与c、b与c的大小关系. 以上是将不等式问题通过构造函数求解,解题思路较为简单.构造函数是高中数学中一种常见的解题方法,那么常见的构造函数方法有哪些呢? 构造函数一直是高考的常考点之一,要想在高考中既快又准地解决问题,必须将构造函数的题型系统化.下面选取了几类高考中较为常见的构造函数的题型,供大家思考和反思. 作差构造法是处理函数问题最基本、最常用的方法,此法一般通过构造函数F(x)=f(x)-g(x),进而转化为F(x)min≥0或F(x)max≤0,从而通过求函数的最值解决问题. 证明先证ln(1+x)≤x.设函数f(x)=ln(1+x)-x,定义域为(-1,+∞),求导得 当-1 当x>-1时, f(x)≤f(0)=0, 即 ln(1+x)-x≤0, 亦即 ln(1+x)≤x. 当-1 g(x)≥g(0)=0, 即 故 评注作差法是常用的证明不等式的函数构造方法.这种方法经常与导数、不等式的性质相结合,主要步骤有3个:一作差,二变形构造,三判断,关键是构造函数并研究其性质.这种题型思路简单明了,易于掌握,是构造函数的基础题型. 例3已知定义在R上的函数f(x)满足f(x)<-f′(x),则下列式子成立的是 ( ) A.f(2 020)>ef(2 021) B.f(2 020) B.ef(2 020)>f(2 021) D.ef(2 020) 解设g(x)=exf(x),求导得 g′(x)=exf(x)+exf′(x)=ex[f(x)+f′(x)]. 因为f(x)<-f′(x),即 f(x)+f′(x)<0, 所以 g′(x)<0, 从而g(x)在R上是减函数.因此, g(2 020)>g(2 021), 即 e2 020f(2 020)>e2 021f(2 021), 变形可得 f(2 020)>ef(2 021). 故选A. 评注这是一道典型的运用导数运算法则构造函数的题目.由f(x)+f′(x)<0可以构造函数g(x)=exf(x),再通过求导研究新函数的单调性,利用单调性比较大小. 导数构造法是近几年高考函数应用中常见的解题方法,也是解决抽象不等式问题的基本方法之一.我们可以通过对不等式的观察研究和深入思考构造出恰当的函数,再研究函数的单调性、周期性和奇偶性等,从而解决问题[1].虽然此类题目变化多样,但也是有一定的规律可循的.可以根据导数的四则运算法则,将其归纳为构造和差型、乘积型、作商型、指数型等函数,具体总结归纳如下: 1)若f′(x)g(x)+f(x)g′(x)>0,则构造函数F(x)=f(x)g(x); 2)若f′(x)±g′(x)>0,则构造函数F(x)=f(x)±g(x); 3)若f′(x)+f(x)>0,则构造函数F(x)=exf(x); 5)若xf′(x)+nf(x)>0,则构造函数F(x)=xnf(x); 变式1定义在R上的函数f(x),其导函数f′(x)满足f′(x)>2f(x),则下列不等式关系正确的是 ( ) A.e2f(-2) 因为f′(x)>2f(x),所以g′(x)>0,从而g(x)在R上单调递增,于是 g(-2) 即 亦即 e2f(-2) 故选项A,B,C正确. 例4若2a+log2a=4b+2log4b,则 ( ) A.a>2bB.a<2bC.a>b2D.a (2020年全国数学高考新课标卷理科试题第12题) 解由2a+log2a=4b+2log4b=22b+log2b,可设f(x)=2x+log2x,则f(x)为增函数,且 f(a)-f(2b)=2a+log2a-(22b+log22b) =22b+log2b-(22b+log22b) 即 f(a) 于是 a<2b. 故选B. 评注例4来自2020年全国数学高考新课标卷理科试题第12题.这种题型的一般形式是一个式子中含有两个变量,通过适当变形后,两边的结构相同,可以取左或取右构造函数,我们把这种题型叫做同构函数题型.同构函数在近几年的高考题中出现较多,要引起重视. 变式2已知函数f(x)=x(x-lnx). 1)讨论f(x)的单调性; (2021年全国数学新高考Ⅰ卷第22题) 评注很明显这道全国卷压轴题的第2)小题考查了同构函数.由blna-alnb=a-b,变形为 b(lna+1)=a(lnb+1), 即 可以构造函数f(x)=x(1-lnx),得 再将此题转化为极值点偏移问题求解,在此就不再赘述. 近两年高考中同构函数的题目反复出现,而且多在选择题和解答题压轴题的位置,一般难度较大,综合性强,学生得分较难.为此,在备考过程中要紧扣教材,掌握函数中常见的解题方法,并学会将各种方法融会贯通,举一反三,这样才能在高考大战中做到游刃有余,立于不败之地! 对于题目中涉及两个变量的问题,我们可以通过题目中的已知条件,将两个变量的和、差、商作为一个新整体设为新变量,构建一个关于新变量的函数,再研究新函数的性质从而解决问题,这样可以把复杂问题简单化. 证明不妨设x1 f(x1)=0,f(x2)=0, 即 两式相减,得 从而 要证 x1+x2+2>2ax1x2, 只需证 即 亦即 所以h(t)在(1,+∞)上单调递增,故 h(t)>h(1)=0, 得证. 评注本题中两个变量x1,x2,再加上参数a,3个变量鼎立,令人心烦,但是三者又有两个方程,虽不能解之,但通过两个方程可以得到三者之间的关系.利用这个桥梁关系进行合理消元进而化为一元函数式,再构造函数求解.消元和化元其实就是一个化繁为简的过程,印证了我们的教学理念“将复杂问题简单化”.除此之外,在其他二元问题上,我们也可以尝试通过消元构造函数或者三角换元,化为一元[2]. 变式3若x,y是实数,且x2-xy+y2=1,求x+2y的取值范围. 分析由x2-xy+y2=1可联想到sin2θ+cos2θ=1,然后用三角换元构造一个新的三角函数,再进行求解. 解题中的等式可以化为 构造函数是近几年高考中的一个热门考点.本文以一道高考题为引例,思考并归纳了几种常见的构造函数的方法,如作差构造函数、导数法则构造函数、同构函数、化双变量为单变量构造函数等,思考将不等式问题、抽象函数问题、双变量问题等转化成常规的函数问题,并利用函数的性质解决问题.在高考备考过程中,我们应该将重点放在培养学生的逻辑思维、推理能力以及化归与转化的能力上,从而使学生能举一反三,并将这些数学思想融会贯通,以后遇到复杂的问题更能懂得如何解决和处理,从而实现真正的素质教育[3].1.1 试题分析
1.2 解题方法探究
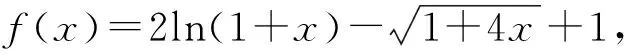
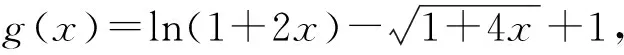
2 探究常见的构造函数的思路与技巧
2.1 作差构造函数
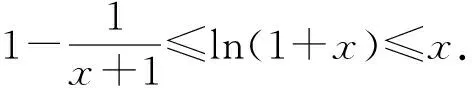

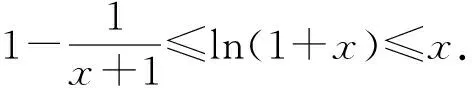
2.2 利用导数的运算法则构造函数


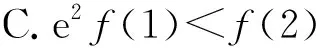

2.3 利用左右形式相当同构函数

2.4 将双变量问题转化成单变量问题构造函数
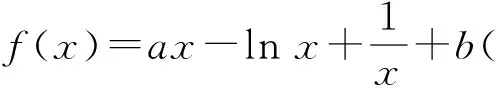


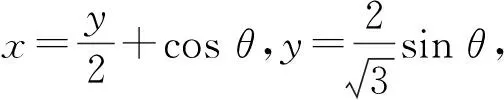

3 小结
——以指数、对数函数同构问题为例

