鳖臑搭起发展直观想象素养的“脚手架”

丁少杰, 杨亢尔

(1．奉化中学，浙江 宁波 315500；2．奉化区教师进修学校，浙江 宁波 315500)

鳖臑最早进入高考命题是在2015年的湖北省数学高考理科试卷，第19题出现了含有“阳马”“鳖臑”古词的立体几何解答题，一时成为热门话题.由于“鳖臑”与“别闹”发音近似，当时有网友对命题者喊出了：“别闹(鳖臑)，回家养马(阳马)吧.”时隔多年，鳖臑几何体已逐渐被人们所接受，并用于立体几何教学，鳖臑数学文化价值也广泛渗透到高中数学的课堂教学与高考试题的命制之中.鳖臑的特殊构造使得它的顶点、棱和面具有丰富的位置关系，从而它成为搭起发展学生直观想象素养的一个“脚手架”.

1 鳖臑的几何内涵

鳖臑最早出现在《九章算术》中，魏晋时期的数学家刘徽在《九章算术·商功》中注释：“此术臑者，背节也，或曰半阳马，其形有似鳖肘，故以名云.”也就是说鳖臑的命名源于它形似甲鱼的前肢[1].因此，通常定义鳖臑为4个面均为直角三角形的三棱锥.这个定义也可等价叙述为：底面为直角三角形，且在底面锐角顶点处有一条侧棱与底面垂直的三棱锥叫作鳖臑[2].图1为刘徽斜分长方体过程的示意图，自左往右的第2幅图到第4幅图分别为壍堵、阳马和鳖臑.

图1

2 鳖臑的教学价值

鳖臑蕴涵了立体几何中点、线、面的各种位置关系，渗透数学文化背景.笔者从领悟垂直关系、掌握“补形”技巧、沟通3类空间角等方面开发鳖臑模型的教学价值，从而探索发展学生直观想象和逻辑推理素养的有效途径.

2.1 领悟垂直关系

空间中的垂直关系是立体几何学习的主线.学生可以在鳖臑几何体中讨论线线垂直、线面垂直和面面垂直以及它们的相互转化，加深这3类垂直关系的理解.

图2

例1如图2，在三棱台ABC-DEF中，平面ACFD⊥平面ABC，∠ACB=∠ACD=45°，DC=2BC．求直线DF与平面DBC所成角的正弦值．

(2020年浙江省数学高考试题第19题)

解如图2，过点D作DO⊥AC于点O，联结OB．过点O作OH⊥BD于点H，联结CH．

由∠ACD=45°，DO⊥AC，得

由平面ACFD⊥平面ABC，得

DO⊥平面ABC，

从而

DO⊥BC．

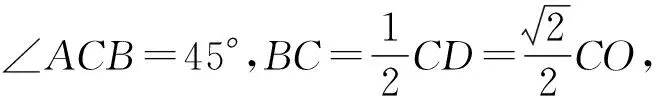
BO⊥BC，

从而

BC⊥平面BDO，

于是

BC⊥DB,

因此，三棱锥D-OBC是一个鳖臑模型.

由三棱台ABC-DEF，得

DF∥CO，

从而直线DF与平面DBC所成的角等于直线CO与平面DBC所成的角.

由BC⊥平面BDO，得

OH⊥BC，

从而

OH⊥平面BCD，

故∠OCH为直线OC与平面DBC所成的角.

从而

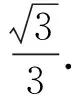
本题求解的关键点在于：1)注意到三棱锥D-BCO为鳖臑，找到目标平面DBC的垂面BDO；2)目标直线DF要平移到直线CO，因为线段CO的长度是可求的.而这两点的发现得益于对鳖臑模型定义的理解.

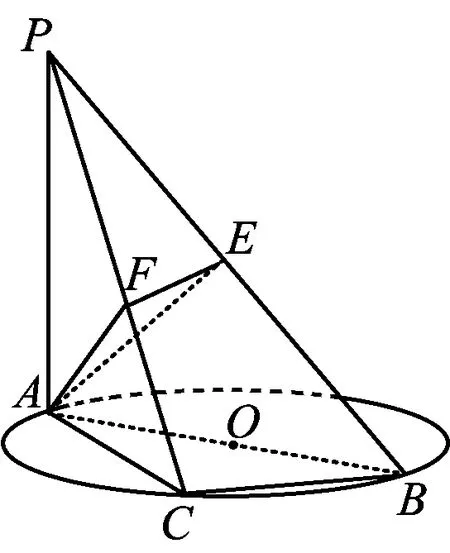
图3

例2如图3，AB是⊙O的直径，PA垂直于⊙O所在的平面，C是⊙O上一动点，过点A作AE⊥PB于点E，AF⊥PC于点F．若PA=AB=2，且平面AEF与平面PAC所成锐二面角为60°，求∠BAC的大小.

变式1删去例2中“平面AEF与平面PAC所成锐二面角为60°”这一条件，求三棱锥P-AEF体积的最大值及此时cos∠BAC的值.

解由已知条件可得

并且PE⊥平面AEF.设AF=x，得

故

例3在中国古代数学著作《九章算术》中，鳖臑是指4个面都是直角三角形的四面体．如图4，在Rt△ABC中，AD为斜边BC上的高，AB=3，AC=4．现将△ABD沿AD翻折成△AB′D，使四面体AB′CD为一个鳖臑，则直线B′D与平面ADC所成角的余弦值是______．

图4

(2021年1月浙江省数学学考试题第21题)

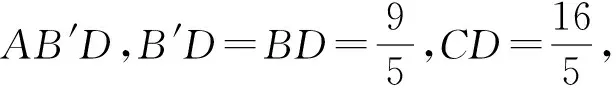
本题中翻折形成四面体的过程实际上是教材中线面垂直判定定理的探究实验，其巧妙地与中国古代数学中的鳖臑概念融合起来，极大地开发了教材资源，全面地考查了学生对空间中垂直关系的理解.

2.2 掌握“补形”技巧典例

鳖臑是切割长方体后形成的几何体，逆向思维，这意味着也可以将鳖臑“补形”成一个长方体(如图5所示).

图5

在鳖臑P-ABC中，PA⊥平面ABC，∠ABC=90°，注意到PA，AB，BC两两垂直，故构造长方体使得PA，AB，BC也为长方体的棱.容易看到，补形后长方体的体积是原来鳖臑体积的6倍，长方体的外接球即鳖臑的外接球，鳖臑的最长棱即长方体的体对角线.因此，鳖臑的最长棱是其外接球的一条直径.这样，就可命制如下问题.

例4《九章算术》中将4个面都为直角三角形的三棱锥称为鳖臑．若三棱锥P-ABC为鳖臑，PA⊥平面ABC，PA=AB=2，且该鳖臑外接球表面积为9π，则该鳖臑表面积为______．

解由鳖臑外接球表面积为9π，得鳖臑的最长棱为3．又PA⊥平面ABC，则底面只有两种情况：

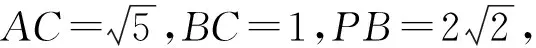
2)∠ACB=90°(图5中B,C标识对调)．此时最长棱为PB=3，而PA=AB=2，这与PA⊥平面ABC矛盾！此种情形舍去.

“补形”是实现复杂几何体转化为简单几何体的重要技巧，然而要掌握它需要学生具备较高层次的直观想象素养.因此，学生应当积累几种经典的补形模型来把握补形的方向.当学生从数学史中了解到鳖臑是切割长方体所得的三棱锥，也就容易理解鳖臑的补形方向是长方体，从而利用长方体来解决鳖臑中的问题.

2.3 架构3类空间角桥梁

由于鳖臑的每个面都是直角三角形，鳖臑中每条棱的计算方法并不唯一.这实际上就沟通了3类空间角：两直线所成角(“线线角”)、直线和平面所成角(“线面角”)以及两平面所成角(“面面角”).为方便说明，用表示两个图形所成角，其中x,y可以为直线或平面．它们的关系可由下面两个公式进行刻画.

1)三余弦公式：若l是平面α的一条斜线，b为平面α内的一条直线，l在α内的射影为a，则

cos=coscos．

在图6中，AC⊥平面α，CD⊥b′，b∥b′，得三棱锥A-BCD为鳖臑，∠ABC,∠CBD,∠ABD分别为,,．对BD“算两次”得

BD=ABcos=ABcoscos，

三余弦公式得证.

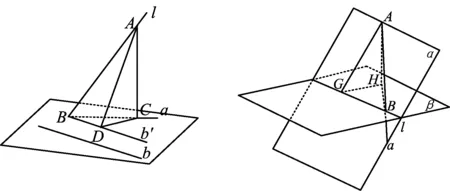
图6 图7

2)三正弦公式：若α∩β=l，a⊂α，则

sin=sinsin<α,β>．

在图7中，AH⊥平面β，HG⊥l，得三棱锥A-HGB为鳖臑，∠ABH,∠AGH,∠ABG分别为,<α,β>,．对AH“算两次”,得

AH=ABsin=ABsinsin<α，β>，

三正弦公式得证.

通过构造鳖臑几何体能优雅而不失条理地对这两个公式进行“无字”证明.进一步挖掘三余弦公式，还有两个“副产物”：

1)三垂线定理及其逆定理，即a⊥b⟺l⊥b；

2)线面角是最小的线线角，即≥=，当且仅当b平行或重合于l在α内的射影a时取等号．

而对于三正弦公式，有推论：面面角是最大的线面角，即≤<α,β>，当且仅当a垂直于α,β的交线l时取等号．

通过上面的证明过程，可以看到鳖臑模型揭示了空间角的本质规律：三余弦公式定量地刻画了线面角和线线角的关系，而三正弦公式定量地刻画了面面角和线线角的关系.运用三余弦、三正弦公式及它们的推论可以解决高考试题中空间角的比大小与求最值问题.

例5已知四棱锥S-ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点(不含端点)，设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S-AB-C的平面角为θ3，则

( )

A．θ1≤θ2≤θ3B．θ3≤θ2≤θ1

C．θ1≤θ3≤θ2D．θ2≤θ3≤θ1

(2018年浙江省数学高考试题第8题)

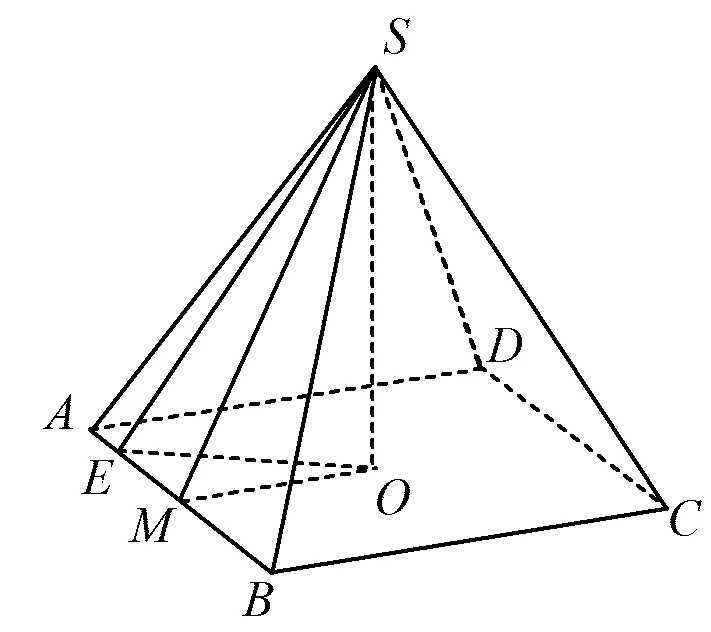
图8

解如图8，取AB的中点M，正方形ABCD的中心O，则SO⊥平面ABCD，OM⊥EM,从而θ1=，θ2=∠SEO，θ3=∠SMO，于是

又由三余弦公式知

cosθ1=cos

=coscos

cosθ1≤cosθ3， sinθ2≤sinθ3

故

θ2≤θ3≤θ1．

当点E与点M不重合时，三棱锥S-OME为鳖臑.

例6如图9，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练．已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小．若AB=15 m，AC=25 m，∠BCM=30°，则tanθ的最大值是______(仰角θ为直线AP与平面ABC所成角).

(2014年浙江省数学高考理科试题第17题)

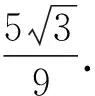
图9

当tanθ取最大值时，三棱锥P-ADC为一个鳖臑，PD⊥平面ABC．

借助空间形式认识事物的位置关系、形态变化与运动规律，是直观想象素养的重要表现形式[3].因此，要进一步提升直观想象素养水平，就需要鳖臑这种形式简单但内涵丰富的空间形式作为媒介发展学生的直观想象素养和逻辑推理素养.

源于中国古代数学专著的鳖臑，是中华民族的文化瑰宝，随着新课程改革的深入，很多学者专家将其融入立体几何教材和高考评价命题之中.立足教材中的经典例题，彰显例题中隐含的数学文化背景，从而激发学生学习的兴趣[4].研究鳖臑的教学价值在于可以加深空间中垂直关系的理解；鳖臑所衍生的内涵足以让学生细细品味垂直关系，让学生深刻感受复杂与简单几何体的互化，也让学生顺利破解千变万化的空间角问题.