“双减”之下几何图形中折叠问题的复习课设计

邓莉莉

(杭州市临平区树兰实验学校，浙江 杭州 311100)

1 现状分析、归纳模型呈现

双减政策之一要求减轻学生的作业量以及作业时长，初中书面作业平均完成时间不超过90分钟.“如何把握高效课堂，如何设计有效的课后作业，明确作业的总量，提高作业设计质量”变得尤为重要.

图形折叠问题的相关知识以及相应解题方式存在于不同的阶段，比较凌乱，不够系统全面.而折叠问题综合性较强，解题思路广，解法又多种多样.为了帮助学生较好地巩固与提升这部分内容，笔者特意分类整理出经典例题——“精选”，以打造高质量、高效率的教学课堂，再以1～2道练习作为课后作业，控制作业的量，有易有难把控作业的难度，优化作业布置，以发挥作业诊断、巩固、学情分析的功能，实现减负高效——真正落实“双减”.

对于例题的分析与评注，体会几何图形的折叠操作，其实就是将几何图形的一部分沿着一条直线翻折180°，使得它与另一个图形在这条直线的同旁完全重合或部分重合，其中“折”是过程，突出了学习过程是一个探究活动的过程；“叠”是一个结果，感知“叠”是另一个结果[1].

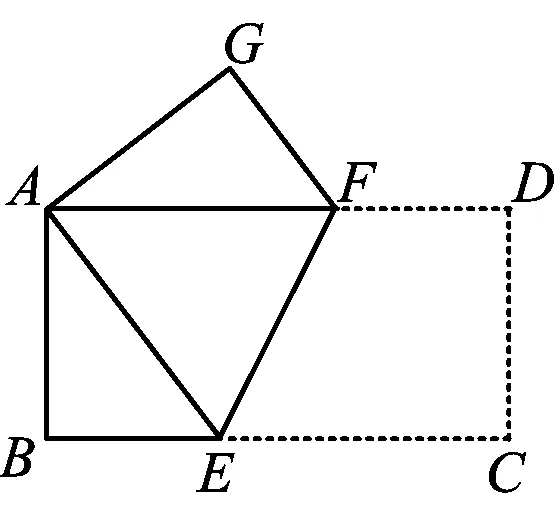
图1

类型1当“折叠”遇到“平行线”，产生“双平等腰三角形”.

例1如图1,在矩形纸片ABCD中，AB=4，BC=8.现将点A与点C重合，折痕为EF，则图形中重叠部分△AEF的面积为多少?

分析由折叠前后互相重合的线段相等可得EC=EA,于是在Rt△ABE中，AB=4，AE+BE=BC=8，通过解直角三角形即可求得AE的长.由折叠前后互相重合的部分是全等图形可得∠AEF=∠CEF,由矩形对边平行可得∠AFE=∠CEF，进而AE=AF，即△AEF为等腰三角形，这样易求图形中重叠部分△AEF的面积.

解根据折叠的相关性质，可设EC=EA=x，则

BE=BC-CE=8-x.

在Rt△ABE中，AB=4,由勾股定理得

BE2+AB2=AE2，

可列方程

42+(8-x)2=x2，

解得x=5，此时EC=EA=5.

由AD∥BC,得

∠AFE=∠CEF,

又∠AEF=∠CEF，从而∠AFE=∠AEF，于是AE=AF,即△AEF为等腰三角形，故

评注本题矩形的折叠强化“折叠后必有角相等，折痕为某一个角的角平分线”这一重要性质.结合矩形的对边平行，利用角度之间的转化，找到等腰三角形，即当“折叠”遇到“平行线”，产生“双平等腰三角形”，找到“AE=AF”，然后再利用“勾股定理列方程”即可解决此模型相关问题.

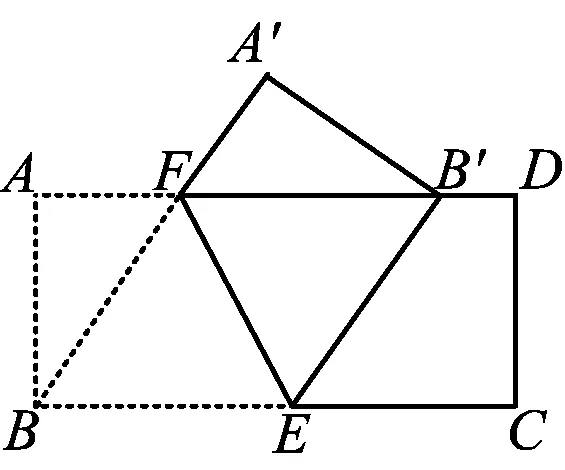
图2

练习1如图2，在矩形ABCD中，AB=4,AD=9,点E在BC上，CE=4，点F是AD上的一个动点，联结BF.若将四边形ABEF沿着EF折叠，点A,B分别落在点A′,B′处，则当点B恰好落在矩形ABCD的边AD上时，AF的长为多少？

类型2当“折叠”遇到“直角三角形”，牵出“勾股定理”.

例2如图3,在矩形ABCD中，AB=4，AD=6，点E为边BC上的一点.将△ABE沿着AE折叠得到△AEF.点H为边CD上的一点，将△CEH沿着EH折叠得到△EHG，且F落在线段EG上.当GF=GH时，求BE的长.

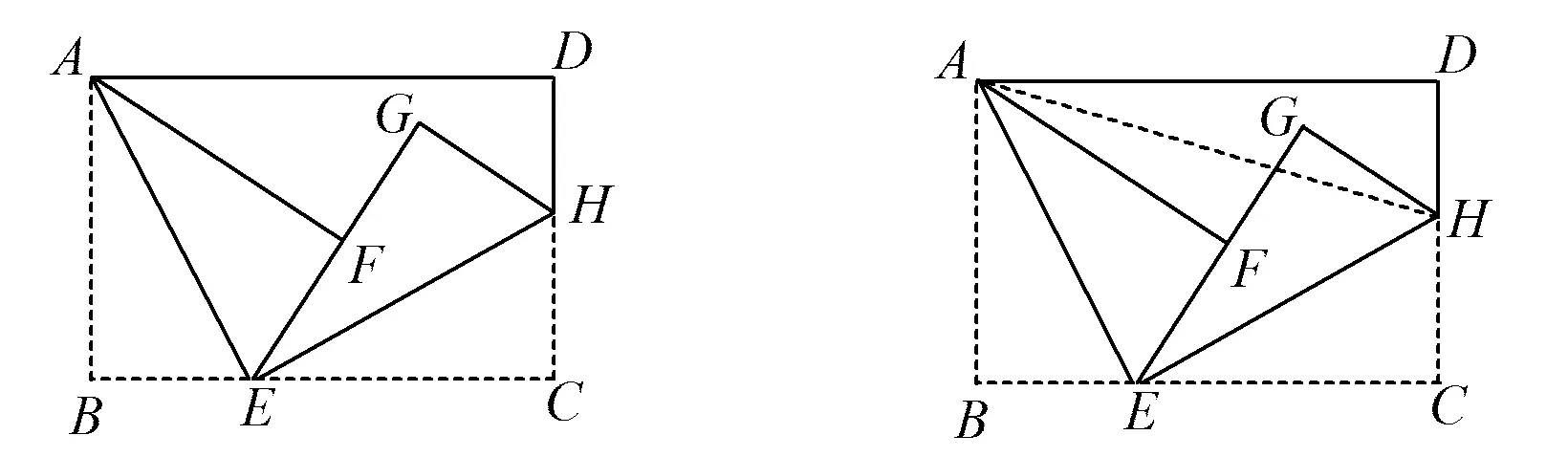
图3 图4

分析由折叠前后三角形全等，得

设BE=x，则

EF=x,CE=6-x=EG.

如图4，联结AH,在Rt△AEH和Rt△ADH中，根据勾股定理AE2+EH2=AH2,AD2+DH2=AH2,即AE2+EH2=AD2+DH2可得方程，解方程即可得到BE的长.

解如图4，联结AH，由折叠可得

BE=FE,EC=EG,GH=CH,

∠AEB=∠AEF, ∠CEH=∠GEH，

从而

设BE=x,则

EF=x，CE=6-x=EG,

从而GF=6-2x=GH=CH,DH=4-(6-2x)=2x-2.

在Rt△AEH中,

AH2=AE2+EH2=BE2+AB2+EC2+CH2,

=x2+42+(6-x)2+(6-2x)2.

(1)

在Rt△ADH中,

AH2=DH2+AD2=(2x-2)2+62，

代入式(1),得

x2+42+(6-x)2+(6-2x)2=(2x-2)2+62，

解得

x1=2,x2=12(舍去).

评注本题是关于矩形的折叠求线段问题，综合性比较强，涉及的知识点较多.设元、利用勾股定理得方程是最常用的方法之一.联结AH，构造Rt△AEH，设所求线段长为x，根据折叠性质用x的代数式表示其他线段，选择适当的三角形，利用勾股定理列出方程求出答案即可.当折叠遇到“直角三角形”，此类型问题的解决离不开勾股定理.

练习2在矩形纸片ABCD中，AB=4,AD=3，点E是CD的中点.将这张纸片依次折叠两次，第一次折叠纸片使得点A与点E重合(如图5),折痕为MN，联结ME，NE，则AN=______;第二次折叠纸片使得点N与点E重合(如图6)，点B落在点B′处，折痕为HG，则BG=______.

(2021年浙江省杭州市临平区二模数学试题第16题)

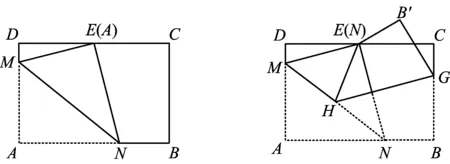
图5 图6

图7 图8

分析先求第1问：由折叠可得

∠MAN=∠MEN=90°.

如图7，过点N作NF⊥DC于点F,在Rt△ENF中，

EF2+NF2=EN2.

设AN=x，则

EN=x=DF,EF=x-2，

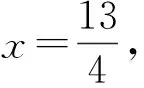
再求第2问：如图8，联结EG,NG，由折叠性质“两对称点的连线被折痕垂直平分”得到EG=NG.设BG=y，CG=3-y，则在Rt△BGN中，

在Rt△ECG中，

EG2=CG2+CE2=(3-y)2+22，

根据EG=NG列方程，进而求得BG.

类型3当“折叠”遇到“正方形”，“十字模型”的呈现.

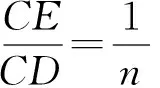
图9 图10

图11

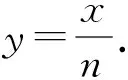
评注本题是有关正方形的折叠问题，是轴对称的性质、正方形的性质、全等三角形的判定与性质等相关知识的综合应用，具有一定的综合性，有助于培养学生的建模思想，从而培养学生的数学素养.在解决本题时，求解的关键在于联结BE，由BE与MN的互相垂直和“十字模型”构造全等三角形，得BE=MN.因此，当“折叠”遇到正方形，若出现“十字模型”，则线段相等，这是解题的关键所在.熟记相关基本图形以及结论会给解题带来极大的帮助.

图12

练习3如图12，将正方形ABCD折叠，使得点A落在边CD上的点E处，折痕为FG，点F在边AD上.若BG=2 cm,DE=3 cm,求折痕GF的长.

类型4当“折叠”遇到“等分点”时，构造“相似三角形”.

例4如图13，在菱形ABCD中，∠B=60°,AD=6,E是BC上一点，且BE=2EC,联结AE，以AE为折痕将△ABE对折，点B′是点B的对称点,EB′与CD相交于点F,则CF=______.

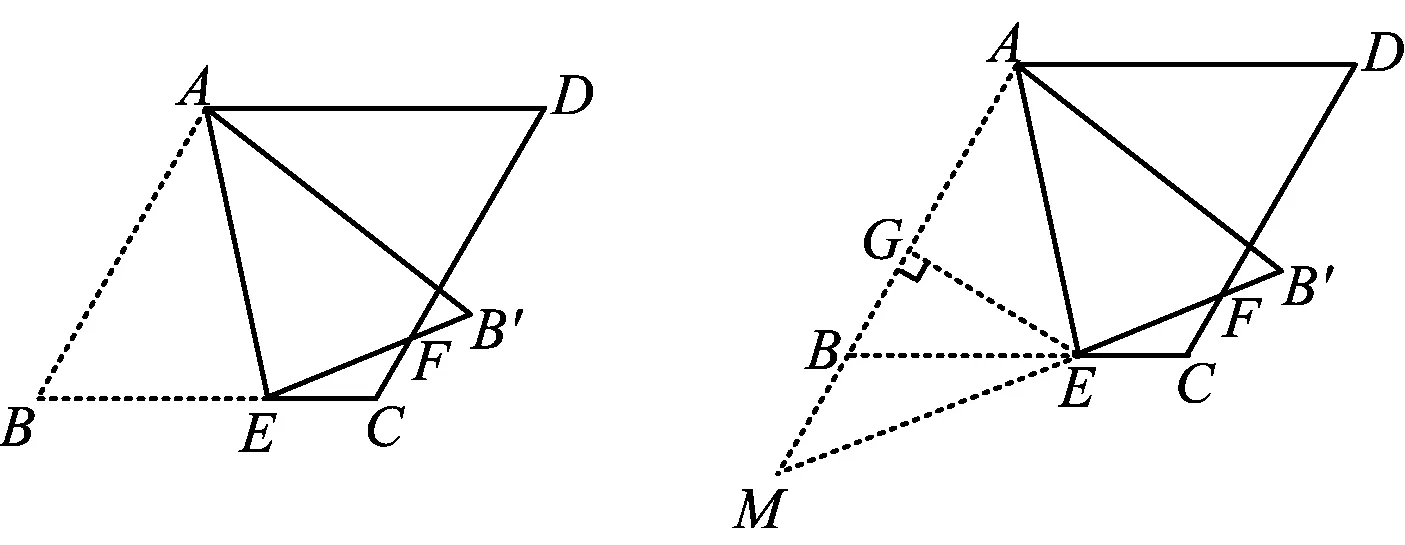
图13 图14

解如图14，延长B′E交AB的延长线于点M.由AB∥CD，得

△MBE∽△FCE，

从而

设CF=x，则

MB=2CF=2x,

由折叠得

△ABE≌△AB′E，

于是

∠MAE=∠EAB′.

根据角平分线等分线段定理,得

则

解得

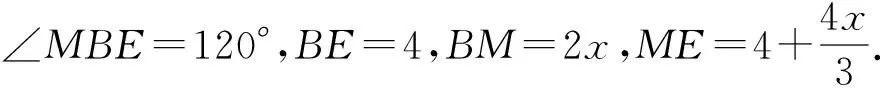
思路1(构造直角三角形列方程求解)在Rt△EMG中，根据勾股定理ME2=EG2+MG2,可得方程

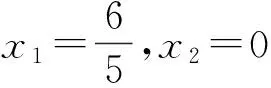
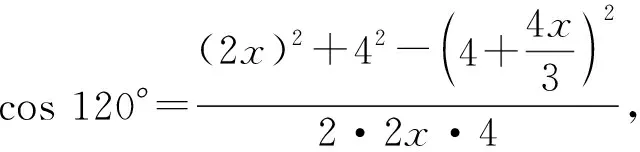
同样可求x的值.

图15

评注本题是关于菱形的折叠问题，题目的综合性比较强，难度较大.关键之处在于当“折叠”遇到“等分点”时，构造“相似三角形”求边，再次强化“折叠后必有角相等，折痕为某一个角的角平分线”这一重要性质，由角平分线等分线段定理实现由角来导边，从而求出ME的长.最后在△BEM中，已知3条边以及一个角，利用“构造法”或“余弦定理”求出x的值.本题考查学生综合应用数学知识和数学建模的能力，有助于培养学生的研究精神，提高学生的几何直观素养.

练习4如图15，在菱形纸片ABCD中，AB=4,∠A=60°，将菱形纸片进行折叠,使点A落在边CD的中点E处，折痕为FG,点F，G分别在边AB，AD上，则EG=______,FG=______.

图16

类型5当“折叠”遇到“动点”时，找出“隐形圆”.

例5如图16,在△ABC中，∠BAC=30°,∠ACB=45°，AB=2，点P从点A出发沿着AB方向运动，到达点B停止运动.联结CP，点A关于直线CP的对称点为点A′，联结A′C,A′P.在运动过程中，点A′到直线AB的距离的最大值为______(如图17)；当点P到达点B时，线段A′P扫过的面积为______(如图18).

分析1)通过分析点A′的运动轨迹，是以点C为圆心、AC的长为半径的圆弧，从而求解；2)画出相应的图形，利用扇形面积和三角形面积公式计算求解.

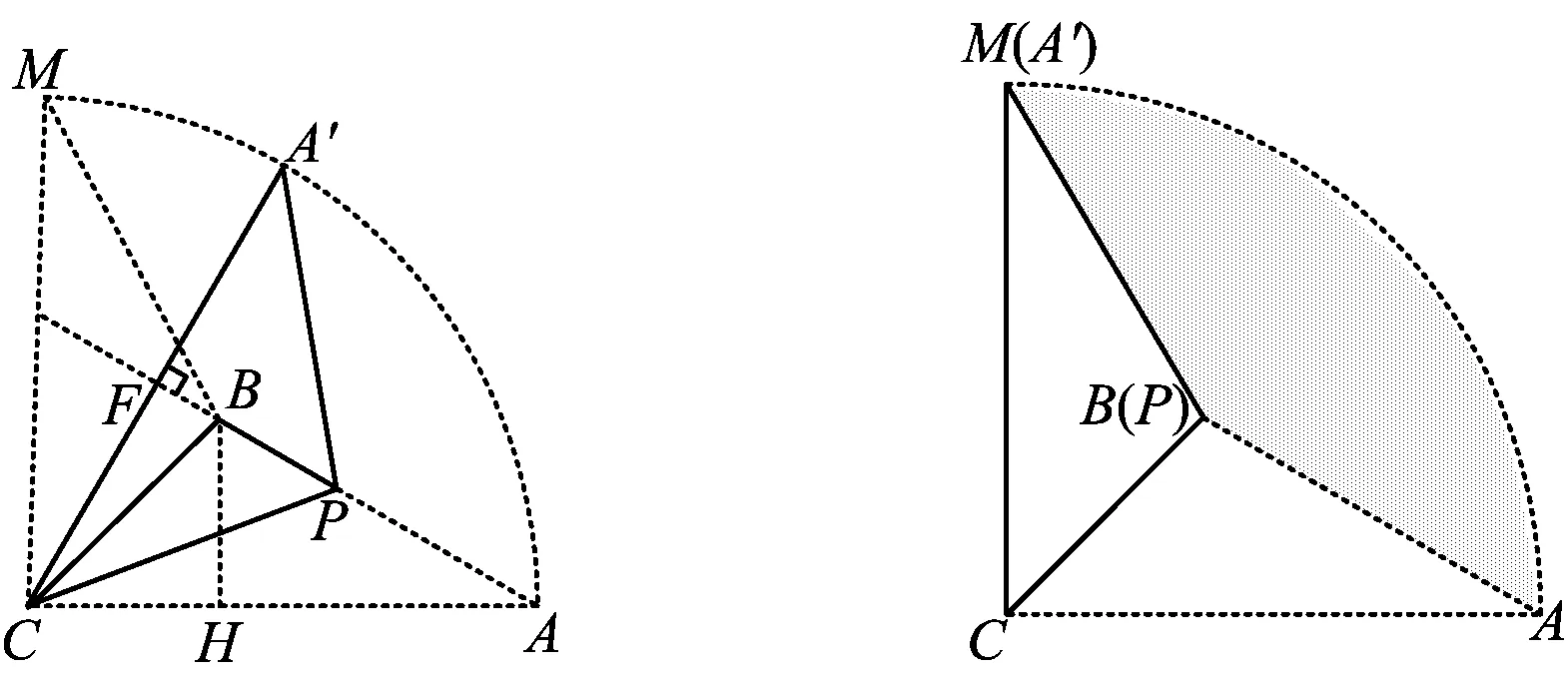
图17 图18

因为点P从点A出发沿AB方向运动，到达点B时停止运动,又因为∠ACB=45°，点A关于直线CP的对称点为点A′，所以∠A′CA的最大值为90°.当CA′⊥AB时，点A′到直线AB的距离最大.

在△ACF中，

2)当点P到达点B时，线段A′P扫过的面积为

评注本题主要考查三角形的折叠问题，结合三角函数边角互化、找到对称点的运动轨迹(是直线还是曲线)，做到“动中求静”.这里的“静”是不变量，要分清“到线的距离不变”还是“到点的距离不变”，再利用端值确定圆弧的两端，最后确定图形形状并求其面积；熟练掌握三角形的性质和折叠(轴对称)的性质是解题的关键.当“折叠”遇到“动点”问题时，找出不变量即“隐形圆或弧”，再来确定动点的运动轨迹，这也是解决此类问题的关键.

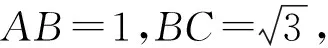
图19 图20

分析先判断出点C的对称点C′的运动轨迹，即“动中求静”：点C′在以点B为圆心、BC的长为半径的圆弧上运动，再利用端值找到圆弧的两端，即“确定图形”(如图20).最后，利用扇形面积公式以及三角形面积公式求出相关面积.

类型6“折叠”后的分类讨论.

例6如图21,正方形ABCD的边长是2，点E是边CD上的中点，点F是边BC上一动点(与点B,C不重合)，把∠C沿着直线EF折叠，使得点C落在点C′处.当△ADC′为等腰三角形时，求CF的长.

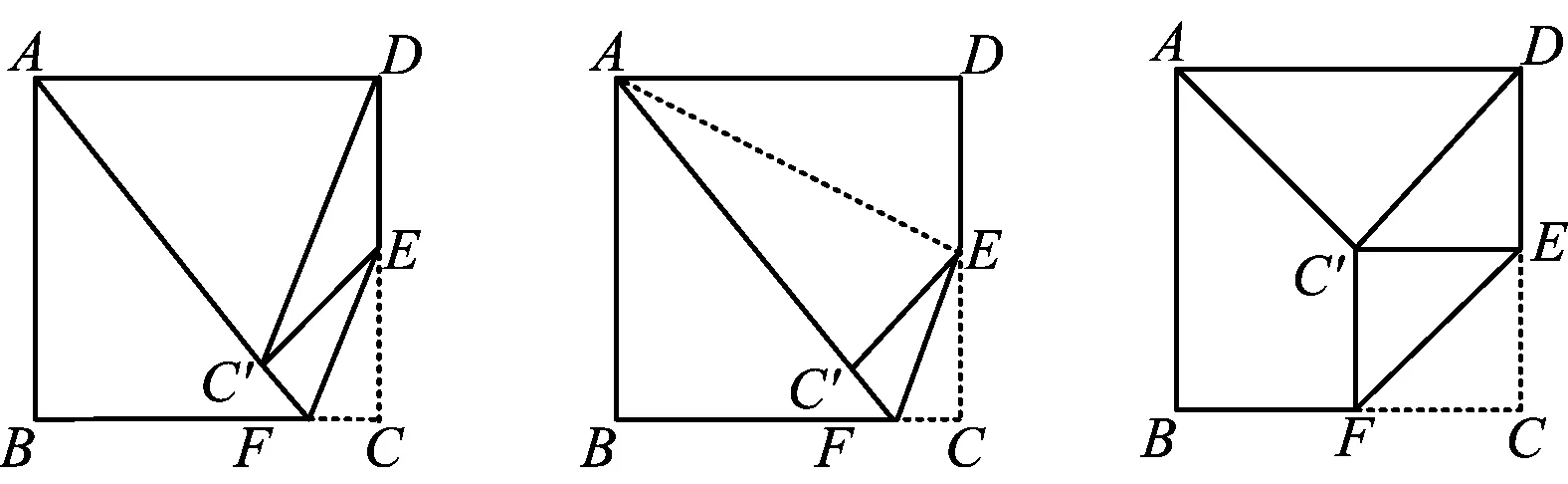
图21 图22 图23

分析由折叠前后的三角形全等可得CE=C′E=1，得C′D<1+1=2，进而C′D≠AD，只要分两种情况进行分类讨论即可：1)如图22,当AD=AC′=2时，联结AE，构建方程即可；2)如图23，当点F是BC的中点时，易证AC′=DC′满足条件.

解由题意可得DE=EC=EC′=1，从而

C′D<1+1=2,

于是

C′D≠AD,

因此△ADC′为等腰三角形的情况只有两种：AD=AC′和C′D=AC′.

1)联结AE.因为AE=AE,AD=AC′，DE=EC′,所以

△ADE≌△AC′E(SSS),

从而

∠ADE=∠AC′E=90°.

又∠C=∠EC′F=90°，于是

∠AC′E+∠FC′E=180°，

即点A,C′,F共线.

设CF=x，则

BF=2-x，AF=2+x.

在Rt△ABF中，由勾股定理得

22+(2-x)2=(2+x)2，

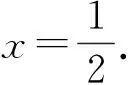
2)当C′D=AC′时，点F为BC的中点，此时CF=1.

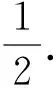
评注本题是三角形的折叠问题.结合正方形的性质，运用勾股定理以及分类讨论的思想是解决此问题的关键所在.折叠问题中的分类讨论是难点也是重点，情况的缺失往往是失分点.

图24

2 教学评价

在“双减”政策之下，对于初三几何复习的教学，笔者认为要做好以下几点：以“高立意、低起点、深探究”为原则,以精心挑选的“例题”+精心设计的“练习”的模式实施教学，紧紧围绕“双减”政策，减少学生的作业负担，作业要精心设计符合教学内容.这节复习课的主要思想是突出“深度体验+彰显方法+感悟思想”这3个关键点，让学生深刻体会，培养思想之“萌芽”；教师彰显方法，助力思想之“破土”；学生灵活应用方法，浇灌思想使之“成长”.

3 教学反思与启示

以上的教学设计较符合学生的学习基础，通过实践尝试，不管是例题内容的安排还是练习的难度设计及量的把控，都能激起学生对折叠问题的兴趣，同时通过课后对练习的批改反馈出课后学生对几何图形折叠问题掌握良好，正确率明显提高，也符合“双减”政策——实现高效率教学.通过课后调查反馈数据呈现：在全班49人中，有38位学生认为这样的课程安排针对性强，效果好，自己收获很大，在遇到类似问题时会想起相关模型；有8位学生的课后作业中依然有错，他们认为还得花时间消化一下；还有3位学生觉得太难了不会做.遇到这样的问题，学生由原来的内心恐惧到现在愿意动笔去尝试，进步很大.

笔者所任教两个班级中考之后，根据第16题的答题情况进行统计.两个班级参加中考的实际学生人数为93人，其中答题正确人数为90人，正确率接近96.78%.但是其中有5人是通过实际测量得出正确答案，还有4人是通过三角函数等较为复杂的方法得出答案，有3人完全不会得0分.再次证明折叠问题不再是难点，难易适中，作业题量适中，知识点概括全面.

图形变换能较好地考查学生的直观想象、逻辑推理和分析、解决问题的能力.而折叠(轴对称)是其中较为复杂的一种图形全等变换，也是学生学习初中几何知识的一大难点.关于折叠(轴对称)的题型较为广泛，本文采用例题的形式，分6类对问题进行细化：可以引导学生深度学习折叠(轴对称)的基本性质，形成几何直观意识，从而强化学生的数学推理能力.

教师要以创新的精神开拓思路，以研究的态度投身实践，从解题术、解题方法到数学思想、数学观念，关注学生的思维过程，抓住数学的本质，以“基础扎实、思维灵动、自信阳光”为目标.改善几何教学可以从以下3个方面努力：

3.1 寻找题中的“蛛丝马迹”

数学解题都是有迹可循的，题目中的条件以及结论(包括图形)都会为解决问题提供相关线索[2].在平时的教学中，教师多引导学生动手画图，并让学生在图中作出标记，在提高学生动手操作能力的同时也有助于学生寻找解题的相关思路.数学思维往往渗透在知识的背后，让学生感受“显”的知识和“隐”的数学思想方法二者之间是相辅相成的，欣赏数学之趣与美，提升数学素养.

3.2 深入思考问题，构建解题模型

深入思考解决问题的方法，激发学生的创新意识，让学生体验成功解决数学问题的快乐与喜悦.挖掘试题的本质，深化知识理解，自主构建解题模型，提升实践能力和创新意识.将几何中的各种模型进行整理归纳，由特殊到一般进行推广，从而提升学生分析问题、解决问题的能力，真正提高其数学核心素养[3].

3.3 提升数学表达能力

数学语言分文字语言、符号语言和图形语言这3种.数学表达能力的提升即数学语言的运用能力，包括数学语言的识读能力、数学语言的转换能力、数学语言的应用能力，主要培养学生“清晰地说、规范地写”，这也是数学核心素养的重要组成部分.