以概念教学为抓手，落实数学核心素养

刘有德

[摘  要] 随着新教育理念的践行，核心素养视域下的数学教育应重视培养学生的各项数学能力，对这些能力的培养是时代赋予我们的重任. 文章认为在核心素养的引领下，概念教学的实施主要有：关注概念形成，形成数学抽象;立足概念表达，建构数学模型;利用数学思想，培养直观想象;注重概念生成，获得逻辑推理.

[关键词] 概念教学;核心素养;深度学习

概念教学属于学科基础性教学，教學的重心在于学生对概念的理解与应用. 在核心素养的背景下，如何创新概念教学模式，构建深度学习课堂，值得每个教育工作者深思. 本文对如何以数学概念教学为抓手，落实核心素养的相关要素谈一些看法.

[] 关注概念形成，形成数学抽象

概念抽象的内容、过程与结果等，是人的思维对概念本质的再现，体现了人脑对数学内容的逻辑性的自然反应[1]. 因此，概念教学时，教师可引导学生以教材为逻辑的线索，关注概念的形成过程，为帮助学生形成良好的数学抽象能力奠定基础.

新课标强调：教学过程中，应关注学生对基本概念与思想的掌握程度，一些核心概念或思想要注重其形成过程，并让这种思想贯穿于教学的始终，让学生在亲历中不断深化理解. 但高中数学概念一般都具有高度的抽象性，教师在引导学生感知概念的形成过程时，应结合学生的认知水平，有梯度地进行引导，让学生在具体实例中感知、抽象出概念的本质.

波利亚认为：知识的学习，最好的方式就是自主发现. 为概念教学搭建具体的模型，能有效促进概念的抽象，让学生对概念产生直观、形象的认识. 鉴于此，教师可通过具体事物引发学生体验、分析与概括，让学生自主获得概念的属性，为抽象概括能力的形成与创新意识的发展奠定基础.

案例1 “任意角的三角函数”的教学

教材提出一些周期运动现象可用三角函数刻画，但没有具体阐述任意角的三角函数概念的形成过程，而是直接以定义的形式呈现，这会让学生无法对其产生深刻的理解. 为此，笔者结合学生的生活经验创设了以下情境.

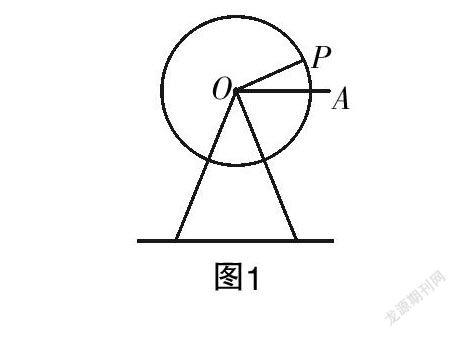
如图1，一座摩天轮的中心点与地面的垂直距离为h，该摩天轮的直径为2r，若按照逆时针方向一直匀速旋转，每旋转一周需360s，一个座舱从初始位置点A出发，求该座舱运动时间与相对于地面的高度h之间的关系式.

为了让学生体会任意角的三角函数概念的形成过程，教师可点拨学生从t=20、30、70秒时h的式子进行思考，逐步抽象出h=h+rsint的猜想，并鼓励学生针对猜想进行分析与验证，同时激发学生对t>90时利用该式计算与原有认知的矛盾，让学主动发现h与t之间究竟存在怎样的关系.

随着探究的深入，学生对任意角的三角函数概念的形成过程有了直观、形象的认识，从而获得完整的概念. 此过程即数学抽象的过程，从具体事物背景中，以及图形与图形或数量与数量之间抽象出概念，获得一般性的规律和知识结构. 学生的抽象能力在概念的抽象过程中得以有效发展，为核心素养的形成奠定基础.

[⇩] 立足概念表达，建构数学模型

数学建模是指学习者根据实际的问题建立模型，在求解该模型的基础上，反之用该模型再去解决其他实际问题的过程. 从某种意义上来说，数学概念其实就是最优的数学模型，概念形成过程的探索，也是建模过程的探究. 克莱因认为：任何一个模型的建构之前，都会经历艰苦、漫长的探索过程[2]. 若认识到这一点，则学生在学习中不仅能获得相应的知识，还能获得攻克问题的勇气.

案例2 “等差数列”的概念教学

问题：观察以下数列，先填空，再说说它们之间具有怎样的共同点与性质，并试着给它们起个名字.

①1，2，3，4，…___，…;②3，6，9， 12，…___，…;③-1，-3，-5，-7，-9、…___，-13…;④2，2，2，2，___，2，2，….

给出几个具体的等差数列，让学生从中发现共性特征，从而抽象出等差数列的基本特性，这为建立等差数列的概念打下了基础. 学生从感性认识中，经历“具体问题—总结、归纳特性—概念形成”，也就是“实际模型—抽象特征—优化模型”的过程. 反之，通过对具体模型的观察，还可促使学生总结、提炼、归纳出概念的本质属性.

[⇩] 利用数学思想，获得直观想象

数形结合思想是重要的数学思想之一，它可以借助几何图形将数量关系直观地展现出来，也可以借助精确的数量关系，清晰刻画直观的图形. 直观想象是指学习者借助几何的直观特性与一定的空间想象，感知数学事物基本形态的过程. 学生对概念的认识，首先建立在对概念感性认识的基础上，然后结合生活实际，通过观察、分析、提炼来认识概念.

数形结合思想在概念教学中的应用非常丰富，学生对图形的认识一般经历从整体出发，到对局部的认识，或从特殊出发，到对一般的认识. 利用数形结合思想开展概念教学，一般遵循直观感知、合作探究、思辨论证、提炼抽象几个步骤.

案例3 “两直线垂直的条件”教学

在学生的认知中，满足两直线垂直的条件为：若直线l，l的斜率分别为k，k，则kk=-1是这两条直线垂直的充要条件. 至于该结论的几何意义，一直未引起学生的注意. 为此，教材中特以几何图形的方式，呈现出以下解释：

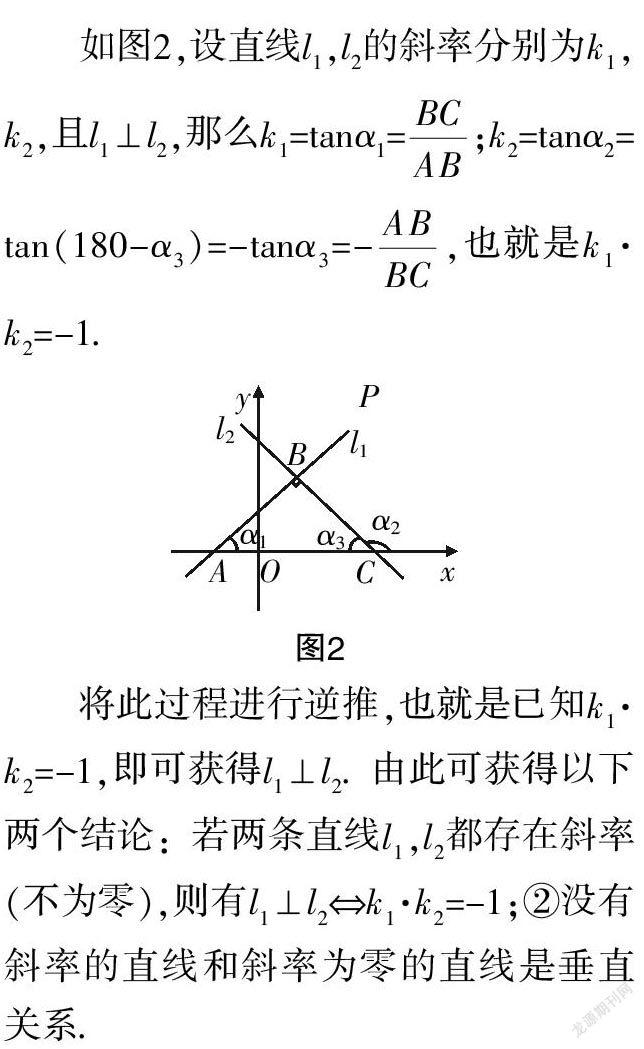
如图2，设直线l，l的斜率分别为k，k，且l⊥l，那么k=tanα=;k=tanα=tan（180-α）=-tanα=-，也就是k·k=-1.

将此过程进行逆推，也就是已知k·k=-1，即可获得l⊥l. 由此可获得以下两个结论：若两条直线l，l都存在斜率（不为零），则有l⊥l⇔k·k=-1;②没有斜率的直线和斜率为零的直线是垂直关系.

这种表达能让学生更加直观形象地认识并理解两直线垂直的条件，为知识的灵活应用奠定基础. 而学生的直观想象能力也在数形结合的探索中得以有效发展，为核心素养的形成夯实了基础.

[⇩] 注重概念生成，获得逻辑推理

概念是发展学生思维，促进学生各项数学能力形成的基础，也是学生形成良好判断能力与逻辑推理的起点[3]. 概念的生成需要严密的逻辑推理能力作为支撑，它对培养学生的数学思维具有重要作用.

案例4 “线面垂直”的概念教学

对于此概念，学生本就有一定的感性认识，如桥柱与水面的位置关系、路灯与地面的位置关系等，从这些生活实际中很容易抽象出线面垂直的直观形象. 虽说对此概念的理解比较容易，但抽象此概念的思维历程还是有一定难度的. 为了实现概念的有效生成，以培养学生的逻辑推理能力，笔者设计了以下几个递进式的教学活动.

1. 用线刻画线面垂直的关系

首先引导学生回忆直线与平面之间的位置关系存在哪几种，常见的有线面相交、线在面内与线面平行三种，从而感知线面垂直为特殊的线面相交关系. 但怎么才能刻画出“不斜”的线面关系呢？有学生认为垂直或90°的线面关系是“不斜”的. 那么这个直角的顶点在哪里？边又在哪里呢？学生带着这样的思考，进行下一步的探究.

2. 线与平面上的线存在垂直关系

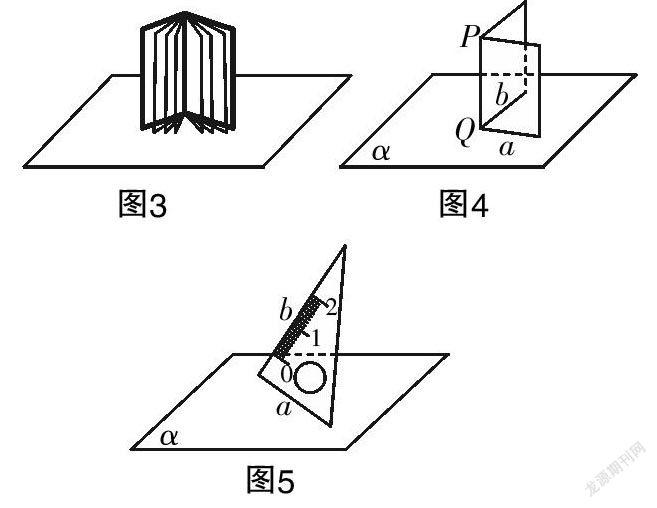
實验：①如图3，立放于桌面的书本，书脊、页面所在的直线与桌面的交线垂直;②如图4，将一张卡纸进行对折，微张立于讲台上，卡纸形成的折痕PQ所在的直线和纸张落于桌面的线段a，b所在的直线垂直;③如图5，将直角三角尺斜立于桌面，一条直角边a位于桌面，另一条直角边b与边a平行的所有直线均为垂直关系，但边b所在的直线与桌面并非垂直的关系.

以上几个探究活动，让学生从直观中逐渐推导出线面垂直的准确概念. 从此推导过程来看，概念的逻辑推理涉及名称、例证、性质与定义四个方面，其中例证涵盖了正例与反例. 一般正例利于学生确定所学概念的内涵，反例可反映出概念的非本质属性，概念的内涵与外延则在正例、反例的应用中有效生成，逻辑推理能力也由此得以发展.

总之，核心素养视域下的数学概念教学，不仅能促使学生更好地理解与掌握概念的内涵与外延，还能有效地调动学生学习的主动性，让学生充分发挥其学习的主体性作用，形成可持续发展的学习能力.

参考文献：

[1]  李兴贵，王富英. 数学概念学习的基本过程[J] .数学通报，2014，53 （02）：5-8.

[2]  科斯塔，卡利克. 思维习惯[M]. 李添，赵立波，张树东，胡晓毅，等译.北京：中国轻工业出版社，2006.

[3]  史宁中. 学科核心素养的培养与教学——以数学学科核心素养的培养为例[J]. 中小学管理，2017（01）：35-37.

3603501908244