培养中学生数学建模能力的实践与思考

吴贻赞

【摘要】通常认为，数学建模是将现实中的问题抽象出数学模型，再通过构建的模型来预测或解决相关问题，数学建模作为现行教育目标之一，充分体现出一个学生的综合运用知识能力和创造力。本文由一道三角函数应用题为背景，引导学生通过读题、联想、计算到构建数学模型这一具体的建模实践过程，探究在课堂教学中如何多方面、多途径培养学生的数学建模能力。

【关键词】数学建模;数学核心素养;数学思想

数学建模作为现行教育目标之一能充分体现一个学生综合运用知识的能力，并且能体现一个人的创造和创新能力，因此，越来越受到国内外教育专家的重视。通常认为，数学建模是将现实生活中的问题抽象出数学模型对未来相关量进行预测和预报。然而，建模过程相对复杂，思维跨度比较大，同时受多种因素制约，学生对建模信心不足、兴趣不高。本文通过一道三角函数应用题教学事例为切入点，探讨在课堂教学中如何多方面、多途径培养学生的数学建模能力。

一、课堂教学简录

1.创设情境，引向建模

通过上一节课的学习，学生知道运用三角函数模型可以刻画匀速圆周运动、简谐运动和交流电流变化现象，体会到数学的应用性。那如何将现实中的问题抽象出数学模型，运用模型来解决相关问题呢？结合学生认知特点，创设简单实际的生活事例情境，获得学生最大关注，激起学生对问题的探究欲望。

师：生活中存在很多周而复始的现象，通过前面的学习，我们知道可以通过三角函数模型来刻画这一变化规律。现实中有这样一个问题：海水受日月引力的作用，会发生潮起潮落。受潮起潮落的影响，码头水深与当天时间有一定关系，同学们能否通过收集数据建立起水深与时间的关系？探讨一下，如果你是船长的话，知道船的安全吃水深度（船底与水面的距离）能否计算，船何时回港口是安全的？

学生陷入思考中。

2.阅读领悟，提炼建模信息

接下来，以教材为根本，首先给足时间让学生阅读新教材必修第一册第245-246页例题2，再次通过有目的的提问，引导学生思考。

师：请大家阅读第245-246页例题2。例2：海水受日月的引力，在一定的时候发生涨落的现象叫潮。一般地，早潮叫潮，晚潮叫汐。在通常情况下，船在涨潮时驶进航道，靠近码头;卸货后，在落潮时返回海洋。

选用一个函数来近似描述这一天该港口的水深与时间的关系，给出整点时水深的近似值（精确到0.001m）。

师：这是一道实际应用题，需要我们把它转化成数学模型，然后利用模型来预测整点时刻水深，这就是通常所说的数学建模。通过阅读，我们要研究的是什么问题？

生1：预测整点时刻，某港口水深。

师：有上表收集的数据，结合变化规律，能否预测某整点的水深？

生2：可以。

生3：不行，不够准确，只是估计与猜测，偏差大。

师：上表收集的数据是具体时刻与对应的水深，这里要研究的也是时刻与水深两变量关系，表格也是表示变量关系的一种形式，但它不能很好地刻画变量之间的变化趋势与准确关系，也就无法相对准确地对因变量进行预测，那怎样才能达到比较准确地预报呢？

生4：求出函数关系式，利用函数关系式进行预测。

师：非常好，接下来，我们构建时刻与水深的函数关系式。

3.思考与计算，构建模型

师：如何构建时刻与水深的函数关系式？

生5：收集数据。

生6：把收集到的数据进行整理，便于观察它们的变化。

师：很好，這是我们进行研究的两变量，甚至多变量关系的前提，要从实际中收集数据，数据收集越多越精确就越贴近真实性，通过大量的数据整理分析，由具体量化寻找他们内在的联系，那又如何比较便捷直观地观察量的变化，确定量之间的关系呢？

生7：通过列表画图。

师：很好，画图，图象直观易观察，准确说，是画它们的散点图，因为我们收集的是离散的数据。题中已收集了一些数据，大家可以利用已有数据画出散点图。

在教师的启发下，学生画出散点图。（以横轴表示时刻，纵轴表示水深）

师：我们作出两变量的散点图后，同学们思考下，这些点呈什么样的分布？大致在什么函数图象上波动？也就是说用数学函数模型刻画出两者关系？

学生有的在思考，有的在讨论。

生8：点上下波动，用正弦函数来刻画。

生9：用余弦函数来刻画。

生10：他们说的都不对，这些点不是分布在正弦、余弦函数图像上，可以看成是正弦函数图像进行伸缩平移变化得到的，可以拟定两者函数关系为。

师：很好，可以看出在函数“”图像上波动，我们拟定时刻与水深的数学模型为。

师：接下来，我们通过收集数据计算出题中参数。

学生在教师引导下选取数据并结合相关知识计算出参数，得到具体的函数关系式。由于学生的差异性，算出的结果可能不同，这就要求学生返回检查重新计算，同时也存在学生认知的差异性。学生拟合的数学模型有所不同，甚至得出错误的结论。所以，我们还要引导学生对所构建的模型进行检验，发现与事情相悖的，倒回第一步，重新构模型。

4.拓展运用，体验建模意义

在师生共同的探究下，得出某港口某天水深与时刻可用近似来描述。

师：通过构建的函数，大家预测下整点时刻8：00，14：00，16：00此处港口的水深。

学生通过计算器计算出相应时刻对应的水深，亲历建模过程，体会到利用科学知识构建数学模型来预测量相对准确性，体验收获成功的喜悦，激励学生对问题的探索。

二、关于课堂教学中培养学生建模能力的认识与思考

1.创设情境，激发学生求知欲与建模兴趣

培养数学建模素养首先要激起学生对问题的兴趣与产生解决问题的欲望。因此，在课堂教学中，教师要根据课堂内容与学生心理特点，设置故事、问题式、悬疑式等相关情境教学，获取学生最佳注意力，引起学生对问题的兴趣，激发学生去解决问题的欲望，调动学生的积极参与。

通过设置情境，抛出问题，引发学生思考，激发学生的求知欲。让学生对学习目标更加明确，并初步了解数学建模意义。但是如何建模，大部分学生的思路是模糊的，怎么将现实问题转化成我们的数学模型？学生表现出浓厚兴趣的同时又感到抽象而陌生。这就需要教师进一步引导，通过问题情境引入问题，导向本节课目标，为下一步数学建模进行铺垫。

2.改进教学形式与评价体系，激励学生大胆探索

数学建模在于对知识的构建与运用，重在学生的参与，将课堂单一教学形式变成开放式、活动式、探索式、实践式多种师生交融性教育，让每个个体在教师的引导下参与讨论问题与解决问题，亦可通过小组合作、师生互评、生生互评的形式发挥学生主体性，让课堂变成生动活泼、交流合作、自主构建知识、创造性发展的课堂。

改变教师对学生单向单一的学习评价，教学上要让学生敢于质疑、参与讨论，激励学生对问题进行大胆的猜想，如何抽象函数模型，鼓励学生通过所学的储备知识对问题进行联想，大胆设想出模型，并参与讨论和论证。同时，让学生用构建的模型来预测相关问题或解决实际问题，体验劳动成果，获得成功的满足感，让学生在数学建模上取得更大的信心。

3.重视知识积累归纳与运用

由于数学建模将现实问题抽象成数学模型，考查学生综合运用知识能力与抽象能力，思维跨度性大，这就要求学生对知识的牢固掌握与灵活运用。学生储备知识的丰富性及对知识的运用对建模起到重要作用，是数学建模的根基，因此，对数学基本知识、基本技能的掌握不可忘本逐末。在培养学生建模素养时，要注重学生对知识的归纳与总结、对方法的提炼，适当引起学生回忆学过的基本函数类型有哪些？求解函数解式方法有哪些，等等。只有在脑海中有了相关数学问题与模型才能将实际问题转化抽象出数学模型来。因此，数学建模能力的培养要从打下牢固基础知识开始。

4.提高学生读想算基本能力

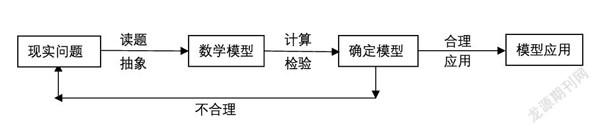
数学建模过程大致要经过以下过程：读题—抽象（猜想）数学模型—确定（计算并检验）数学模型—数学模型应用，如下图所示：

在课堂教学中，多样式、多方法丰富学生阅读，加强学生抽象思维能力与计算能力的训练，来发展学生的数学建模能力。

首先要通过阅读、审题提取题中的重要信息，读懂题是解决问题的前提，数学建模问题，往往给出现实生活中的实际问题，内容可能包括理、工、农等学科相关知识，涉及范围广、综合性强，变量隐于其中，变量之间关系不明确，对学生阅读理解的能力要求高。教学上，要有目的地培养学生自主阅读理解能力，克服畏惧心理，鼓励学生在阅读后大胆发表自己的观点与想法，通过提问的方式引导学生抓住题中重要信息;也可以通過小组讨论合作的方式互帮互助、取长补短，提高阅读能力;也可以通过设置有趣的情境活动，先粗读再细读，唤醒学生阅读兴趣，提出有用信息。初步明确要研究的量，为后续建模打下基础。

其次，鼓励学生结合知识储备大胆联想出数学模型，用数学关系式或思想方法去概述现实生活问题。对初学的学生来说，缺乏方向性和操作性，思维跨度大，将具体问题一步抽象出数学模型也是不符合实际的。教师要明白建模的具体步骤，过程细化到可操作性。例如，通过散点图形式将抽象问题具体化，让学生有依可想，想得明白，想得出来。从而逐步培养学生的抽象概括能力。

最后，明晰运算对象，依据运算法则计算出拟合模型中的相关参数，对数学模型进行辩证思考，是否合理性、有无缺失问题、存在的偏差等，对问题进行思考论证，对于不切实际的、错误的问题，要返回重新进行拟合关系，重复上述过程直到问题解决。在这一过程中，学生需要正确面对理论与实际生活中存在的偏差问题。

数学建模是将实际问题通过提炼概括抽象构建并计算出数学模型，再利用模型解决相关问题这样一系列的实践过程，过程复杂而抽象，是学生对知识综合运用和创造力的重要体现。提高学生数学建模素养，应遵循循序渐进的原则，不能一蹴而就，应从提高学生兴趣与意识着手，着重提高基本知识与基本技能，遵从学生的认知特点。这是一个由易到难、逐步提高的过程。

参考文献：

[1]教育部.普通高中数学课程标准（2017年版）[S].人民教育出版社，2018.

[2]孙宏安.数学高考试题情境设计分析[J].中学数学教学参考（上旬），2019（1）：6.

[3]邵光华，蒋周渠.数学建模素养评价模型与案例分析[J].中学数学教育（高中版），2020（4）：3-10.

责任编辑  梁国胜

1959501705340