高等学校课程思政建设探索与实践——以大学数学为例

杨立星，李玉霞

(泰山科技学院，山东 泰安 271038)

数学课程是高校的一门公共基础课程，培养学生具备科学严谨的治学态度，激发学生对数学课程的好奇心和求知欲，培养创新的思想意识，掌握数学相关课程的基本知识、基本理论和基本方法，使学生具有抽象概括能力、逻辑推理能力、空间想象能力、自学能力、熟练的运算能力以及综合运用所学知识及数学方法分析问题和解决问题的能力。学生普遍反映在学习过程中困难较多，内容抽象，主动学习的意愿不强，学习兴趣不高。介于此，可以引入一定的思政元素(数学故事、实际生活中的例子、数学文化等)，起到润滑剂的作用，丰富课程内容，在提高学生学习积极性的同时，对学生进行德育教育。

1 潜移默化，将思政元素融入数学知识讲解中

案例1：已知抗病毒药物甲、乙均包括A、B、C三种成分，且每种成分所占比例如表1所示。

表1 成分所占比例Tab.1 Proportion of the constituents

2 讲好中国故事，弘扬中国精神

案例2：高等数学课堂在讲解“曲线凹凸性”这一内容时，可从如下案例引入。

港珠澳大桥横穿大海，宛若一条长龙飞向天际。这条长桥是中国从桥梁大国走向桥梁强国的里程碑之作，被称为“现代世界七大奇迹”之一。

可以将桥抽象成一条曲线，研究这条曲线的常见特性，如图1所示。除了单调性外，曲线的主要特征如图2所示。

图1Fig.1

图2Fig.2

接下来就可进入重点知识讲解，利用导数研究曲线的凹凸性。除了得到数学结论之外，在课堂上还可以将问题进行延伸，让学生思考为什么港珠澳大桥是弯弯曲曲，而不是笔直的？这就涉及生态保护(中华白海豚)、安全性(桥墩受海水冲击力的方向)等问题。通过对这些问题进行解释，让学生认识到国家在环境保护方面做出的努力以及在很多科研方面我国技术处于世界领先地位，感受大国工匠精神。

3 宣扬中国文化，提升民族自豪感

案例3：极限思想是高等数学的核心思想，导数的概念与定积分的概念均是建立在极限的思想之上的。我国古代思想家、哲学家都对极限有过生动描述，教师在讲解这部分内容时，可以适当引入。

《庄子》

一尺之棰，日取其半，万世不竭。

“万世不竭”虽然与极限趋于常数零有所不合，但“日取其半”很好地给出了极限的变化意境。

《送孟浩然之广陵》

故人西辞黄鹤楼，烟花三月下扬州。

孤帆远影碧空尽，唯见长江天际流。

“孤帆远影碧空尽”很传神地给出了趋向于零的极限意境。

案例4：在讲解极值时，可以通过苏轼的一首古诗《题西林壁》来引入极值的概念。

《题西林壁》

横看成岭侧成峰，远近高低各不同。

不识庐山真面目，只缘身在此山中。

通过诗中的意境及观察图3，可引出极值的定义。

图3Fig.3

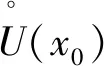
4 结语

专业教育如何融合思政教育是教学改革的重要内容，其核心要义是强调专业类课程通过深入挖掘学科中蕴含的思想政治教育资源，充分发挥专业课程的育人功能和专业课教师的育人职责。在具体教学实践过程中，任课教师应注重立足高等学校数学课程内容，不生搬硬套思政元素，达到思政教育润物细无声的效果。