探索多种方法求18°角的正弦值

陈 城

（湖北黄冈应急管理职业技术学院 湖北·黄冈 438021）

1 求18°角的正弦值的构思

初中学习过锐角三角函数的知识、三角形有关知识、多边形及圆的有关知识，故可以构造平面图形利用平面几何知识求解。还可以利用诱导公式；两角和、差的正弦、余弦公式及倍角公式、正弦定理、余弦定理的知识求解。

2 构造平面图形用初中平面几何知识求解

2.1 方法一：构造顶角是36°的等腰三角形做辅助线求解[1]

实际上，可以用黄金分割比来理解该解法，把一条线段分成两段，使得短线段与长线段之比等于长线段与全线长之比，称为黄金分割比。[2]易算出黄金分割比的比值为.满足黄金分割模型需要同时满足两个条件：（1）最长的线段；（2）长度介于中间的线段的等比中项。两个条件必须同时满足，缺一不可。

图1

2.2 方法二：构造顶角是108°的等腰三角形做辅助线求解

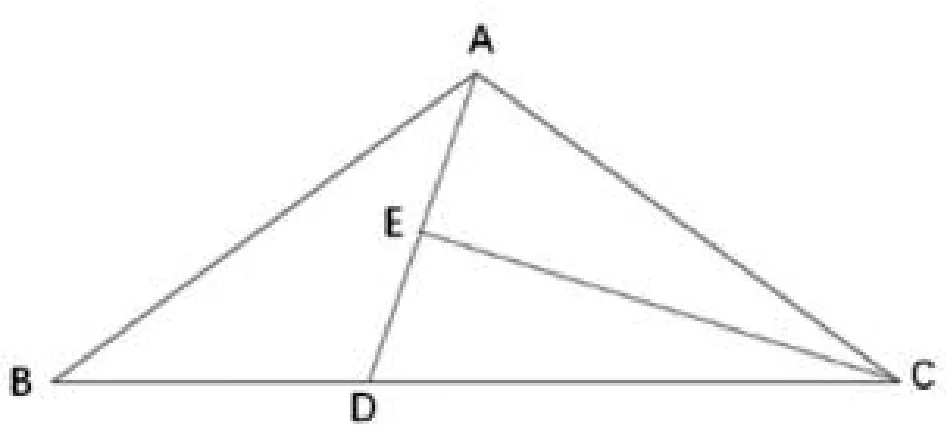
图2

2.3 方法三：构造正五边形做辅助线求解

图3

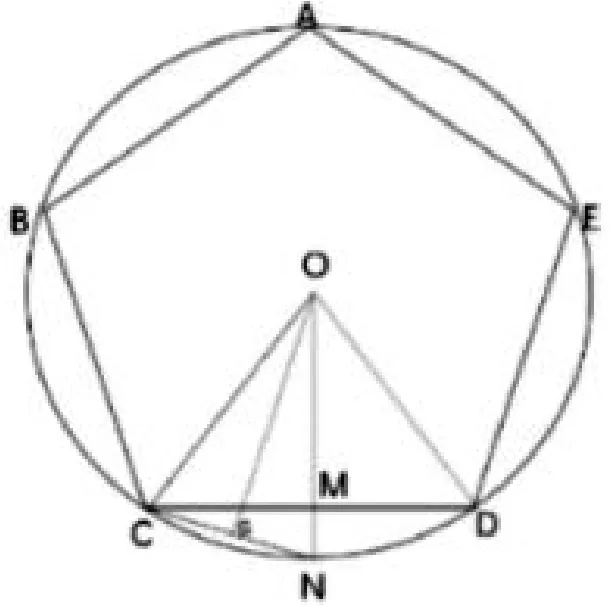
图4

2.4 方法四：构造五角星图形求解

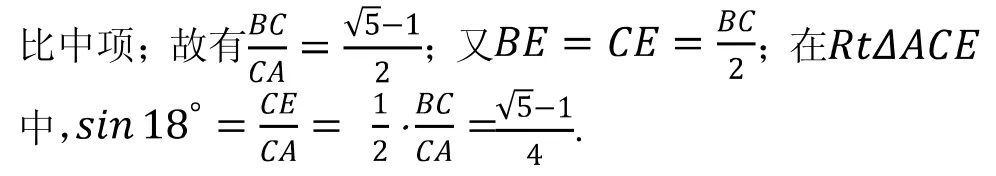
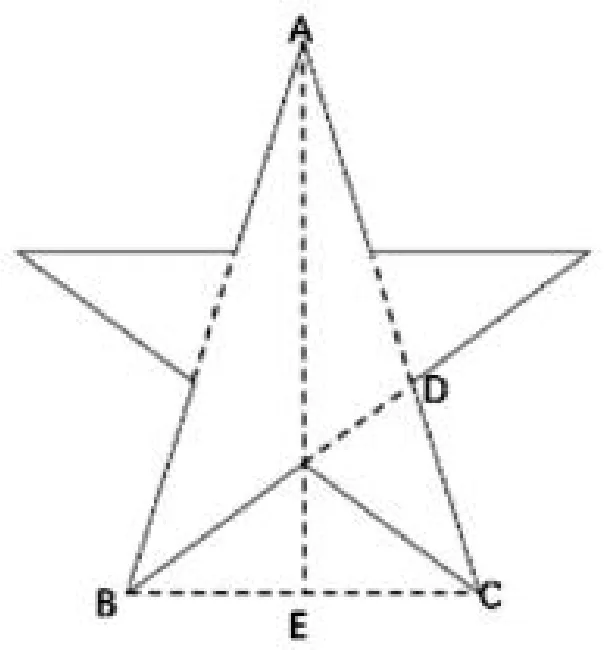
图5

3 利用诱导公式及和差公式、倍角公式、正弦定理与余弦定理求解

3.1 方法五：诱导公式及倍角公式求解

3.2 方法六：诱导公式及倍角公式求解

3.3 方法七：诱导公式及倍角公式求解

3.4 方法八：利用正弦定理、余弦定理结合诱导公式及倍角公式求解

4 小结

求解18°角的正弦值，上述列出的方法均是通过找等量关系列方程，均贯穿了解方程的思想，有些方法构思巧妙就直接化成了一元二次方程求解，而有些方法会出现3次、4次方程，这时必须通过因式分解来化简约去非零因式最终转化成一元二次方程求解。构造的图形，其内角均是18°的倍数，需要巧做辅助线，特别是合理作角平分线、等腰三角形底边上的高。还要灵活运用全等、相识三角形的判定与性质，构造图形求解具有形象直观性；而运用高中的诱导公式、倍角公式等知识点简洁明了，但是比较抽象。