外滚道剥落的高速轴承转子非线性系统及其振动响应分析

谢 聪， 郝丽娜， 邓 松， 钱东升， 华 林

(1. 武汉理工大学 现代汽车零部件技术湖北省重点实验室，武汉 430070；2. 武汉理工大学 汽车零部件技术湖北省协同创新中心，武汉 430070；3. 武汉理工大学 湖北省新能源与智能网联车工程技术研究中心，武汉 430070；4. 武汉理工大学 材料科学与工程学院，武汉 430070)

高速工况下，轴承润滑油膜厚度实时变化导致轴承载荷和变形实时变化，显著影响轴承转子系统运转稳定性和振动噪声水平。因此，建立符合工程实际的滚道剥落高速轴承转子非线性系统模型至关重要。

许多学者对轴承故障动力学模型进行了研究。Liu[1]将轴承滚道剥落引起的时变接触激励、轴承与轴承座接触变形、油膜刚度和阻尼等综合考虑建立滚道剥落的轴承转子系统动力学模型，研究了滚道剥落尺寸对轴承转子系统的附加位移激励的影响规律。罗茂林等[2]建立了外滚道剥落轴承动力学模型，分析了钢球在剥落区滚动全过程动力学行为，获得了剥落引起的时变位移激励函数。常斌全等[3]将钢球进入缺陷到离开缺陷细分为进入事件、冲击事件、离开事件和载荷补偿事件，结合轴承接触刚度和阻尼建立了多事件激励的滚动轴承动力学模型。王文龙等[4]基于弹流润滑理论计算钢球与滚道间的摩擦力，采用短轴轴承理论计算套圈与保持架间摩擦力，并将钢球与保持架接触等效为刚度弹簧来建立角接触球轴承-转子系统的动力学分析模型。Babu等[5]考虑了转子变形、轴承摩擦力矩、滚道波纹度等非线性因素建立了6自由度轴承转子系统振动响应模型，这比刚性转子轴承模型更符合工程实际。Sopanen等[6]考虑了轴承滚道缺陷、钢球激励力和力矩、接触变化和弹流动力润滑等因素建立了深沟球轴承动力学模型，该模型比较符合工程实际需要。Khanam等[7]建立了轴承载荷、轴承转速、轴承缺陷作用下钢球冲击激励模型，并分析了缺陷尺寸、缺陷位置和分布对冲击激励的影响，该模型需考虑高速工况下这些影响因素非线性对钢球冲击的影响。Jiang等[8]根据钢球通过缺陷区时钢球是否与缺陷区域顶边和两侧边接触，对钢球与缺陷接触形式分类，建立了考虑滚钢球与缺陷区域三维几何关系的轴承动力学模型。Qin等[9]考虑了符合工程实际的滚道剥落结合高速状态轴承离心力和时变接触力建立了滚道缺陷高速球轴承动力学模型，该模型需进一步考虑高速下油膜对轴承振动的作用。Liu等[10]考虑了滚道缺陷引起的时变位移，载荷诱导摩擦力矩和润滑诱导摩擦力矩建立了滚动轴承转子系统模型，该模型线性化轴承刚度和阻尼不符合高速状态轴承刚度和阻尼实时变化的特点。Liu等[11]根据滚道波纹度和钢球波纹度推导了轴承时变摩擦力矩计算方法，分析了波纹度对高速轴承动力学作用规律。

上述研究没有结合高速工况和高速下缺陷引起的钢球位移和冲击、油膜刚度和阻尼、滚道变形和接触力等时变特性建立符合工程实际的滚道缺陷高速轴承转子系统非线性动力学模型的相关研究。针对上述问题，本文考虑了高速工况下外滚道剥落引起的时变位移和时变冲击激励、油膜时变刚度和油膜时变阻尼、钢球与滚道接触时变刚度和时变接触力等非线性因素建立了外滚道剥落高速轴承转子系统动力学模型，通过与其他学者研究结论对比分析证明了该模型有效可靠，进而分析了高速和低速工况、外滚道剥落尺寸对该轴承转子系统振动响应的影响规律。

1 外滚道剥落时变位移和时变冲击激励模型

针对滚道剥落早期小凹坑特点结合许多学者考虑缺陷为正方形、圆形[12]的轴承剥落研究现状，考虑缺陷宽度小于长度且缺陷尺寸小于钢球直径的外滚道剥落(如图1所示)建立时变位移激励模型和时变冲击激励模型。外滚道剥落长度为L，宽度为B，深度为H。

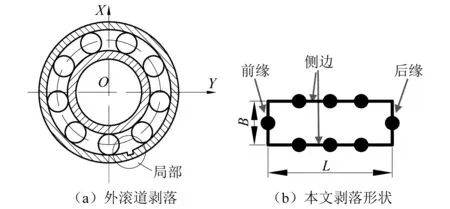
图1 外滚道局部剥落示意图Fig.1 Schematic diagram of partial peeling of the outer raceway

1.1 时变位移激励模型

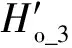
图2 滚动体与局部缺陷相对位置图Fig.2 Relative position map of rolling elements and local defects

钢球滚过剥落过程中附加位移实时变化，根据刘静研究结论采用分段函数表示外滚道剥落下钢球附加位移量[13]，表达公式为

式中：H3为钢球与剥落两侧边接触时产生的最大附加位移量；θj为钢球与外滚道之间位置角；θoo为剥落位置角；ΔTo_1为钢球碰到剥落两侧边到离开剥落两侧边经过的角度；ΔTo_3为钢球从剥落前缘到接触剥落两侧边经过的角度； ΔTo为局部剥落对应的角度ΔTo=arcsin(L/Do)；ωc为保持架转速；n为滚动体个数；j为第j个钢球；D为球的直径；mod( )为求余函数；Do为外滚道直径；θ′oo为第一个钢球与外滚道局部剥落之间的初始位置角。

1.2 时变冲击激励模型

Khanam等指出在滚道剥落前缘接触刚度降低，挠度增加导致一个冲击力发生，这个力称为进入力，钢球沿剥落两侧边滚动过程中进入力持续存在，钢球离开剥落两侧边时这段滚动时间称为钢球进入时间。根据载荷变形关系理论，进入力最大值可用式(2)表示

(2)

式中，kc为载荷位移常数。碰到剥落边缘时产生的最大变形量为

(3)

从钢球碰到剥落前缘到钢球接触剥落两侧边为进入力作用的时间，可以用式(4)和式(5)来计算

(4)

(5)

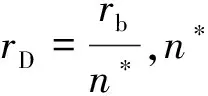
在钢球离开剥落前缘到钢球撞击剥落后缘过程中，钢球始终与剥落两侧边接触，这段时间用式(6)来表示

(6)

Khanam等也指出钢球离开剥落时撞击剥落后缘，由于剥落边缘处刚度较低挠度较大而产生冲击变形，我们将剥落后缘作为一个弹簧，那么钢球撞击后缘时弹簧被压缩。在钢球离开剥落后缘时，弹簧被释放，于是冲击力经过了由小变大再变小的过程。冲击力大小与外部载荷、相对速度和轴承材料属性密切相关。撞击力最大值用式(7)表示

(7)

式中，钢球在剥落后缘时最大压缩量为xo_imax，通过式(8)计算

(8)

撞击剥落后缘瞬间钢球角速度为

(9)

式中:mb为钢球的质量；ωR为钢球自转转速。

从撞击过程可知，撞击时间由两部分组成，分别是撞向剥落后缘产生弹性变形的过程以及变形量恢复钢球滚过剥落后缘的过程，于是撞击时间可由式(10)表示

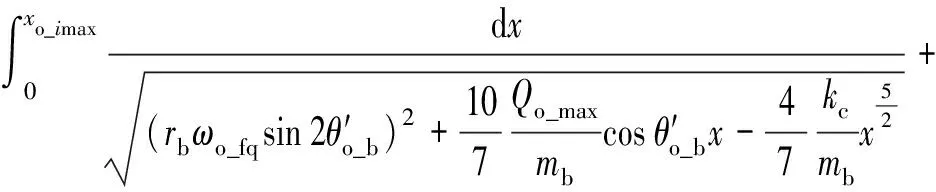
(10)

Khanam等采用分段函数描述钢球冲击力变化过程，表达公式为

(11)

2 外滚道剥落高速轴承转子系统动力学模型建立

在高速工况，钢球与滚道接触时变刚度和阻尼、油膜时变刚度和油膜时变阻尼、摩擦力矩等因素对轴承转子系统动态行为具有显著影响，本文轴承时变刚度和时变阻尼和摩擦力矩采用文献[14]的方法来确定，进而建立考虑时变接触力、时变刚度和时变阻尼等因素作用的高速轴承动力学模型。将外滚道剥落时变位移和时变冲击激励模型与高速球轴承动力学模型结合建立六自由度滚动轴承转子系统动力学模型，如图3所示。背对背安装的轴承采用7308C角接触轴承，左侧轴承外滚道剥落在位置角0°处，轴承参数如表1所示。将钢球与滚道接触模拟成弹簧-阻尼系统，外圈固定，内圈与转子固定旋转。该滚动轴承转子系统沿x，y和z轴平动，并且绕x，y和z轴转动。转子重力方向沿着x轴负方向，建立外滚道剥落轴承转子系统模型参数，如表2所示。

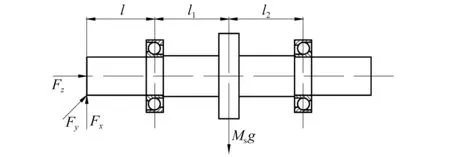
图3 滚动轴承转子系统简化模型Fig.3 Simplified model of rolling bearing rotor system

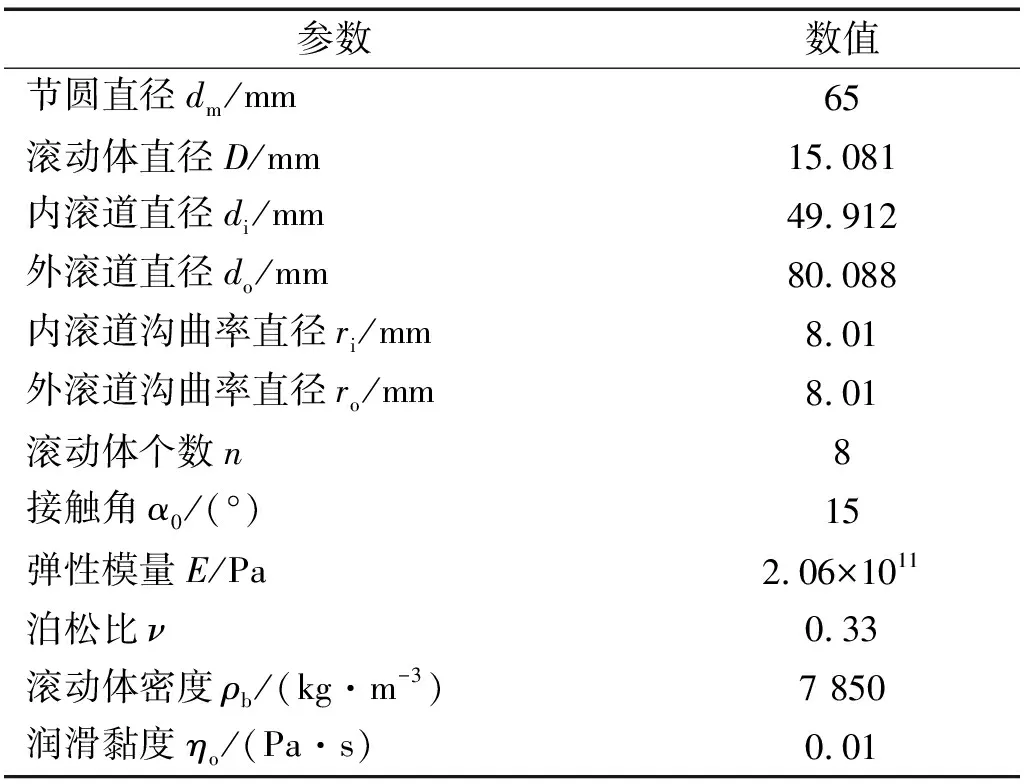
表1 7308C轴承结构、载荷和润滑参数Tab.1 7308C bearing structure, load and lubrication parameters

表2 轴承转子系统参数Tab.2 Bearing rotor system parameters

2.1 钢球与滚道之间的径向位移量的计算

在高速工况下，轴承时变接触角导致任意角位置θj处钢球与滚道之间变形不同，在安装中施加给轴承的预载荷以及运动中由于绕x轴和y轴的摆动导致钢球和内外滚道之间产生的接触位移量实时变化。当钢球位于局部剥落区域时，根据Babu等[15]的研究思想推导了接触位移量的计算公式为

(12)

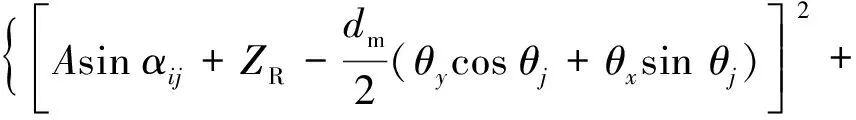
(13)

式中：ξ为判断钢球否在剥落区域，ξ=1表示钢球在剥落区域，ξ=0表示钢球不在剥落区；δ为钢球位移；下标L和R分别为左侧和右侧轴承；XL，XR，YL，YR，ZL，ZR分别为两端轴承内圈沿x，y和z方向的位移。

2.2 滚动轴承转子系统动力学方程组

在外滚道剥落作用下，轴承时变位移激励显著作用钢球与滚道之间接触力。在轴承载荷和转速作用下，考虑外滚道剥落作用的钢球与滚道的时变接触力计算公式为

(14)

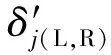
当轴承中某个钢球位于局部缺陷位置处，冲击激励也会对系统产生重要影响。因此，考虑外滚道剥落的轴承转子系统动力学方程为

(15)

式中:Ms为转子质量；Msg为转子质量；Ix为转子在x方向上的转动惯量；Iy为转子在y方向上的转动惯量；Iz为转子在z方向上的转动惯量；Fx为系统所受沿x方向的载荷；Fy为系统所受沿y方向的载荷；Fz为系统所受沿着z方向上的载荷。

外滚道剥落滚动轴承转子系统非线性动力学模型求解流程，如图4所示。首先通过高速球轴承动力学模型计算任意角位置钢球的接触载荷、接触位移、接触角和卷吸速度等，进而求解钢球与滚道接触时变刚度kip，kop。将获得的接触载荷、卷吸速度等时变参量与油膜时变刚度和油膜时变阻尼模型结合，计算油膜时变刚度和油膜时变阻尼，随后确定轴承时变刚度和时变阻尼。通过滚道剥落引起的附加位移和冲击力计算模型确定钢球时变位移和时变冲击激励，进而结合轴承时变刚度和时变阻尼计算轴承时变接触力。最后，通过自适应步长的四阶龙格库塔法求解外滚道剥落的滚动轴承转子系统非线性动力学方程，求解中位移初值选为x0=10-6m，y0=10-6m，z0=10-6m，转速初值选为0。

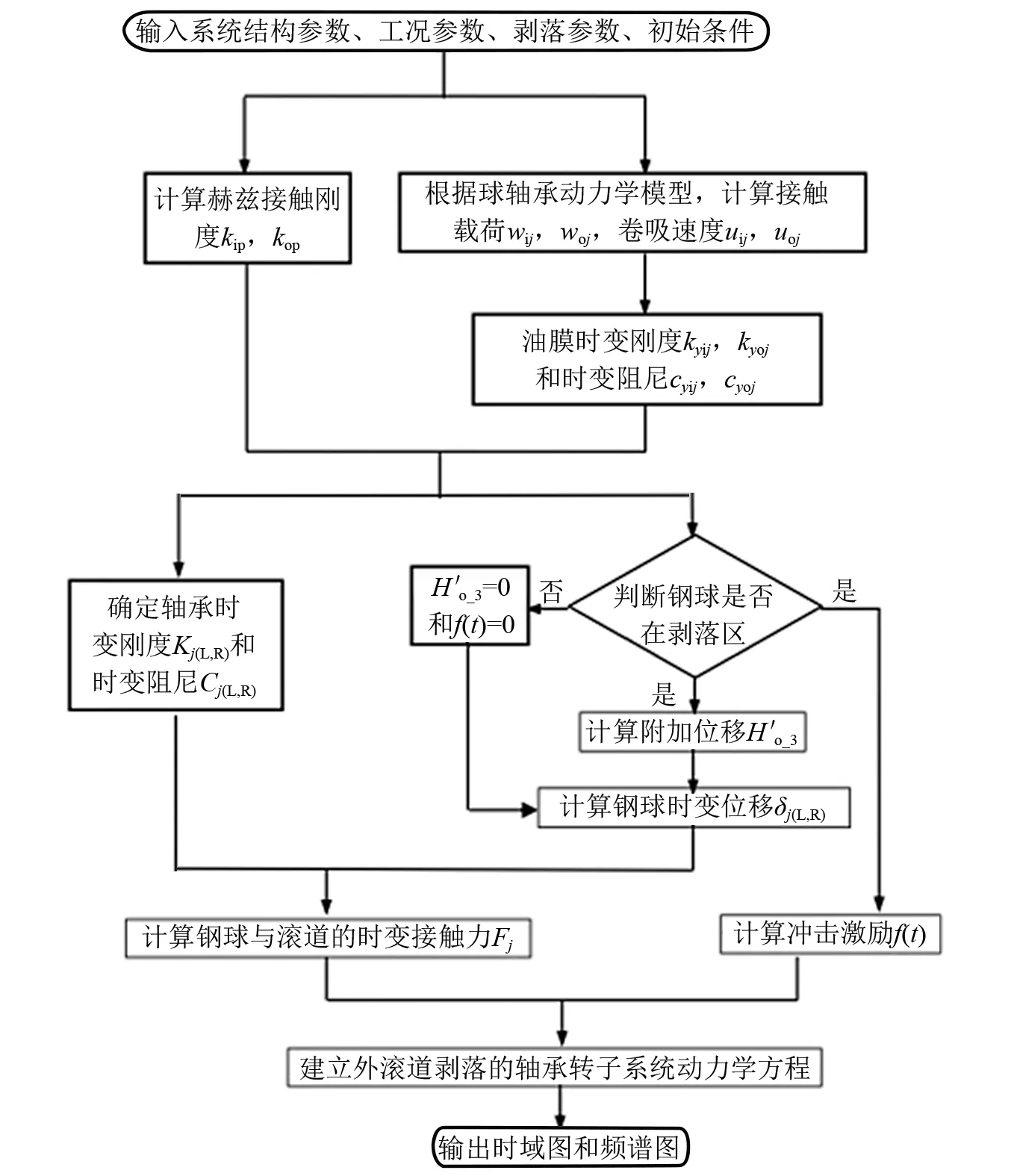
图4 外滚道剥落滚动轴承转子系统动力学模型求解流程图Fig.4 Flowchart of solving the dynamic model of the rolling bearing rotor system of the external raceway

2.3 外滚道剥落滚动轴承转子系统动力学模型有效性验证

在实际工况下，滚道剥落引起的钢球时变位移和时变冲击激励、轴承时变刚度和时变阻尼、时变接触力和摩擦力矩对轴承转子系统的振动响应具有重要影响，建立外滚道剥落滚动轴承转子系统动力学模型对准确研究滚道缺陷作用下轴承转子系统动力学行为至关重要。为了验证高速和低速状态下外滚道剥落滚动轴承转子系统动力学模型有效性，假定外滚道剥落长度L为1 mm，宽度B为0.5 mm，研究转速nn=2 000 r/min和nn=10 000 r/min时本文轴承转子系统模型幅频响应规律。如图5所示，低速状态(nn=2 000 r/min)无剥落情况下钢球通过频率(fs=103.98 Hz)和钢球通过外滚道剥落频率(fsd=103.45 Hz)基本一致，而且它们的谐波频率(2倍、3倍、4倍)基本一致，滚道剥落状态系统振幅明显大于健康状态系统振幅。在高速状态(nn=10 000 r/min)，无剥落情况下轴承转子系统频率和振幅变化规律与滚道剥落状态系统振幅和频率变化规律基本一致。此外，试验测试轴承钢球通过频率(如图6所示)与数值分析结果一致，这表明本文外滚道剥落高速轴承转子系统非线性动力学模型有效可靠。通过对比分析高速和低速时本文轴承转子系统振幅，发现高速时系统振幅相对低速时系统振幅增加了两个数量级，这说明系统转速对滚动轴承转子系统振动行为具有显著影响，综合考虑剥落引起的时变冲击激励、油膜时变刚度和时变阻尼、时变接触力和摩擦力矩等非线性因素建立符合工程实际的滚动轴承转子系统动力学模型具有重要应用价值。

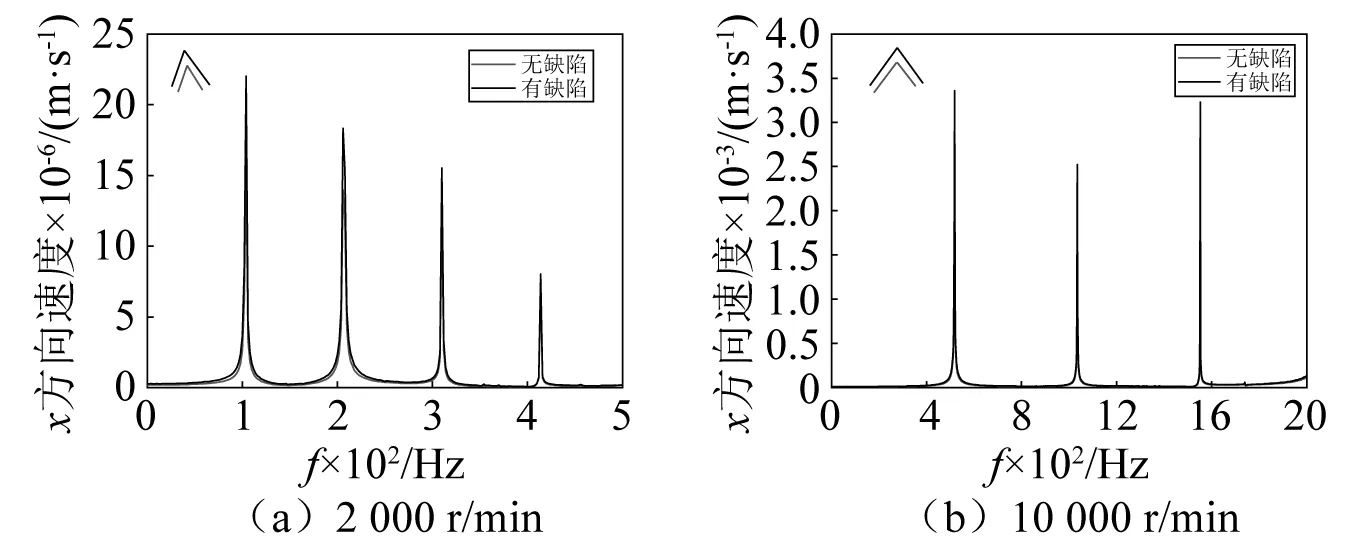
图5 高低速时x方向振动速度频谱Fig.5 Vibration velocity spectrum in x direction at high and low speeds

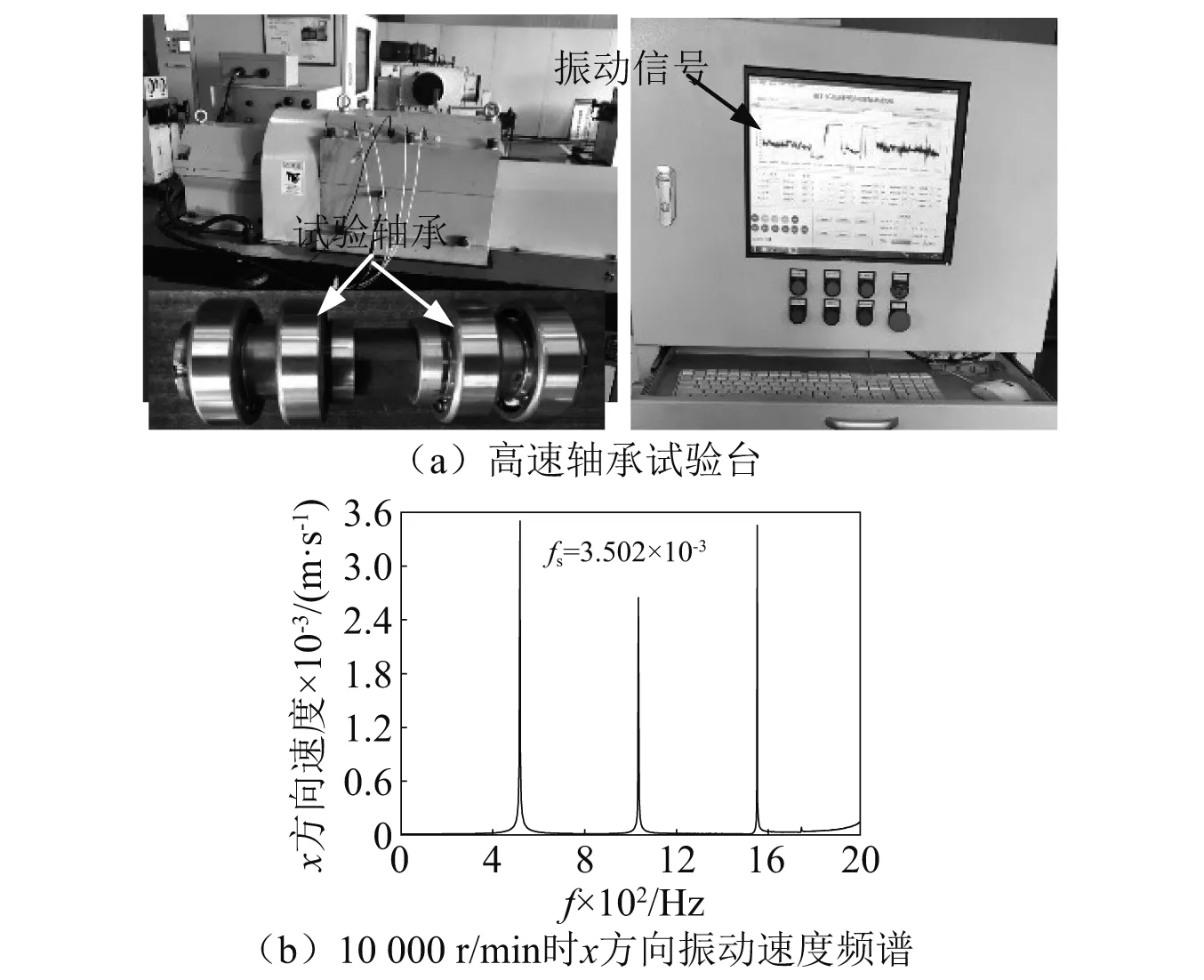
图6 10 000 r/min时轴承振动试验Fig.6 Bearing vibration test at 10 000 r/min

3 结果与讨论

3.1 剥落尺寸对滚动轴承转子系统振动响应影响

图7描述了低高速下不同剥落尺寸对轴承转子系统的振动响应作用。当转速为1 000 r/min时，对比分析图7(a)和图7(b)可知，剥落长度影响钢球进入剥落和退出剥落的时间间隔。此外，当剥落长度为1 mm时，进入振动速度与剥落长度为3 mm时进入振动速度几乎相同，但是退出振动速度明显小于剥落长度为3 mm时的退出振动速度。这是因为剥落长度和宽度较小时，钢球进入剥落区时变位移很小，在退出剥落区时很难产生明显的冲击激励。当剥落长度较大时，钢球沿着剥落两侧边的时变位移增加导致钢球退出剥落区时冲击剥落后缘产生较大的冲击激励，进而引起较大的退出振动速度。对比分析图7(b)和图7(c)可知，当宽度从0.3 mm增加到0.5 mm时，剥落宽度对钢球通过剥落区的时间间隔没有影响，但是宽度的增加导致钢球附加位移量增加，进而加剧钢球冲击激励以致系统振动速度变大。当转速为10 000 r/min时，对比分析图7(d)和图7(e)可知，剥落长度的增加略微增加了系统振动速度幅度。对比分析图7(e)和图7(f)可知，增加剥落宽度也略微增加了系统振动速度幅度。这是因为高速下钢球没有经历剥落引起的完整附加位移导致冲击激励较小，系统进入振动峰值与退出振动峰值差异不大。此外，高速下钢球进入剥落和退出剥落的时间间隔以致进入振动没有衰减历程，钢球退出剥落区后系统振动发生明显衰减。对比高速状态和低速状态系统振动幅度，高速下系统振动幅度是低速下系统振动幅度的2～6倍。这说明高速下轴承时变接触角、时变接触力和摩擦力矩等非线性因素对轴承转子系统振动响应具有重要作用。

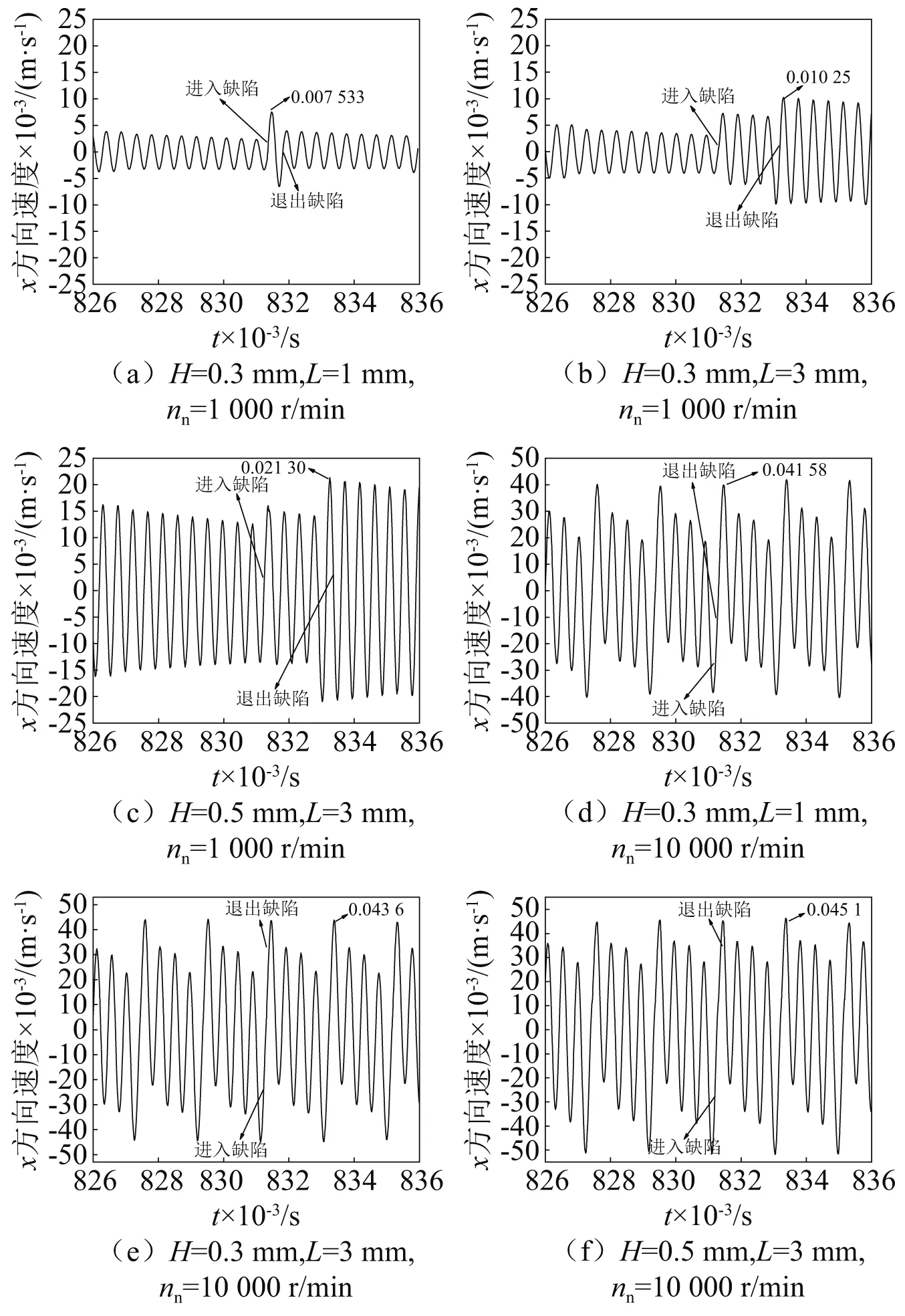
图7 不同剥落尺寸下系统振动速度波形图Fig.7 Waveform diagram of system vibration speed under different exfoliation sizes

3.2 剥落尺寸对滚动轴承转子系统振动均方根和峭度值的影响

为了统计分析轴承转子系统振动响应情况，常采用振动均方根评价振动信号能量和峭度值评价滚道剥落程度。振动均方根计算方程为

(16)

式中:xi为第i个振动位移响应；Nf为振动位移信号的长度。峭度值计算方程为

(17)

式中，mean()为振动信号的平均值。

图8描述了剥落长度为2 mm时不同转速和剥落宽度下轴承转子系统振动均方根值变化规律。由图8可知，当转速一定时，系统振动均方根值随着剥落宽度的增加逐渐增加，这是因为较大的剥落宽度增加了钢球附加位移量，导致钢球的时变位移和时变冲击激励增加，加剧了钢球离开剥落区时的冲击振动能量。此外，当剥落宽度一定时，在低速状态(转速1 000 r/min)系统振动均方根值约1.3×10-4m，在高速状态(转速12 000 r/min)系统振动均方根值约1.7×10-4m，高速状态轴承转子系统振动能量明显大于低速状态系统振动能量，这表明高速状态轴承时变接触角、油膜时变刚度和阻尼、时变接触力等非线性因素对系统振动能量具有显著作用。所以，综合考虑剥落引起的时变冲击激励和时变位移、油膜时变刚度和时变阻尼、时变接触力和摩擦力矩等非线性因素建立符合工程实际的滚动轴承转子系统动力学模型研究高速状态系统振动响应更具有科学意义。

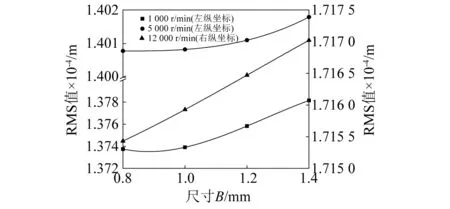
图8 不同转速下剥落宽度对系统振动均方根值影响Fig.8 Effect of peeling width at different speeds on the rms value of system vibration

图9描述了剥落长度为2 mm时不同转速和剥落宽度下轴承转子系统振动峭度值变化规律。由图9可知，当转速一定时，系统振动峭度值随着剥落宽度的增加逐渐减小，这是因为较小剥落宽度时钢球通过周期内系统剧烈振动时间小，通过峭度值评价系统振动形态偏移大；较大剥落宽度时钢球通过周期里系统剧烈振动时间长，通过峭度值评价系统振动形态偏移小。此外，随着剥落宽度增加，低速状态(转速1 000 r/min)系统峭度值变化幅度大，高速状态(转速12 000 r/min)系统峭度值变化幅度小，这是因为高速状态在钢球通过周期内剥落引起的振动没有明显衰减，钢球经过滚道剥落区和非剥落区时振动速度差异不大。因此，在低速状态剥落宽度对轴承转子系统峭度值影响较大，在高速状态剥落宽度对轴承转子系统峭度值影响较小。

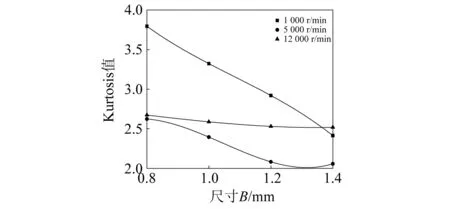
图9 不同转速下剥落宽度对系统振动峭度值的影响Fig.9 Effect of peeling width at different rotation speeds on the system vibration Kurtosis value

图10描述了剥落宽度为0.5 mm时不同转速和剥落长度下轴承转子系统振动均方根值变化规律。由图10可知，当转速为1 000 r/min，剥落长度从1 mm增加到2.5 mm，系统振动均方根值从1.326 48×10-4m增大到1.326 83×10-4m，增加幅度非常小。当转速为12 000 r/min，剥落长度从1 mm增加到2.5 mm，系统振动均方根值从1.682 42×10-4m增大到1.682 79×10-4m，增加幅度非常小。这说明剥落长度对系统振动响应没有明显影响，这是因为剥落长度没有改变钢球附加位移导致钢球时变位移和时变冲击激励变化很小。但是，当转速为1 000 r/min时系统振动均方根值约1.32×10-4m，当转速为12 000 r/min时系统振动均方根值约1.68×10-4m，高速状态系统振动均方根值比低速状态明显增加了0.36×10-4m，这也说明高速状态轴承时变接触角、油膜时变刚度和阻尼、时变接触力等非线性因素对系统振动能量具有显著作用。

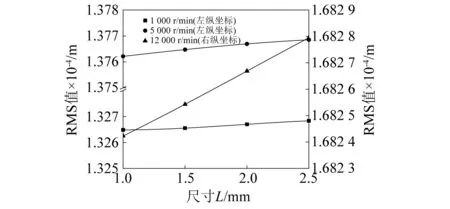
图10 不同转速下剥落长度对系统振动均方根值影响Fig.10 Influence of peeling length at different speeds on the rms value of system vibration

图11描述了剥落宽度为0.5 mm时不同转速和剥落长度下轴承转子系统振动峭度值变化规律。由图11可知，当转速一定时，系统振动峭度值随着剥落长度的增加逐渐增加，这是因为增加剥落长度没有改变钢球附加位移和冲击激励，但是增加了钢球通过剥落区时间以致系统振动可以明显衰减(图7(a)和图7(b)中系统振动速度波形可以说明)，所以较大剥落长度的系统振动形态偏移大于较小剥落长度的系统振动形态偏移。此外，随着剥落长度增加，低速状态(转速1 000 r/min)系统峭度值变化幅度大，高速状态(转速12 000 r/min)系统峭度值变化幅度小，这也是因为高速状态，钢球经过剥落区系统振动没有明显衰减，钢球经过非剥落区系统振动产生明显衰减(见图7(d)所示)。在低速状态，钢球经过剥落区系统振动发生明显衰减，钢球经过非剥落区系统振动幅度没有明显变化(见图7(b)所示)。因此，在低速状态剥落长度对轴承转子系统峭度值影响较大，在高速状态剥落长度对轴承转子系统峭度值影响较小。

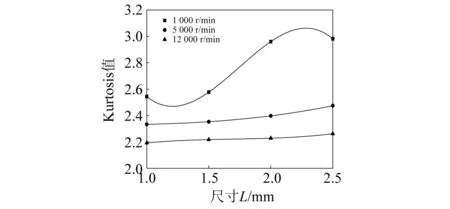
图11 不同转速下剥落宽度对系统振动峭度值的影响Fig.11 Effect of peeling width at different rotation speeds on the system vibration Kurtosis value

4 结 论

(1)将滚道剥落引起的时变位移和时变冲击激励、油膜时变刚度和时变阻尼、钢球与滚道时变接触刚度和时变接触角、时变接触力等非线性因素综合考虑，结合JONES的高速球轴承动力学模型建立了外滚道剥落的高速轴承转子系统非线性动力学模型。研究结果证明建立符合工程实际的滚动轴承转子系统动力学模型具有重要应用价值。

(2)低速状态剥落宽度对钢球通过剥落区的时间间隔没有影响，但是宽度的增加导致钢球附加位移量增加，进而加剧钢球冲击激励以致轴承转子系统振动速度变大；高速状态剥落宽度增加对系统振动速度没有明显影响；高速下系统振动幅度显著大于低速下系统振动幅度。

(3)转速一定时，系统振动能量随着剥落宽度的增加逐渐增加，高速状态轴承转子系统振动能量明显大于低速状态系统振动能量；转速一定时，系统振动峭度值随着剥落宽度的增加逐渐减小，而且低速状态系统峭度值变化幅度大，高速状态系统峭度值变化幅度小。

(4)低速和高速状态，剥落长度对系统振动响应没有明显影响，但是系统振动峭度值随着剥落长度的增加逐渐增加；此外，随着剥落长度增加，低速状态系统峭度值变化幅度大，高速状态系统峭度值变化幅度小。