不同工况下含间隙铰链接触碰撞力特性研究

韩雪艳， 宋敬伟， 高振辉， 魏元浩， 李 铜， 李仕华

(1. 燕山大学 机械工程学院，河北 秦皇岛 066004；2. 燕山大学 河北省并联机器人与机电系统实验室，河北 秦皇岛 066004)

在航空航天领域，机械传动系统对转动副的精度有很高的要求。零部件的加工精度和设备的装配精度，都直接影响到系统的使用性能。因此，研究含间隙铰链接触碰撞力特性对于实际的工程应用具有重要意义。近年来，我国航空航天事业的发展取得了巨大的进步，推动了我国对外太空探索的进程。影响航空航天机构精度的因素很多，如间隙、运动副元素间表面粗糙度、重力环境等，因此在分析机构的性能时，应该进行不同工况环境下的仿真分析和试验研究，为机构的精密设计和精确控制提供理论依据。

近些年来，国内外许多学者对含间隙机构的动力学性能进行了研究，阎绍泽等[1]对目前的研究成果进行了总结，阐述了不同碰撞模型的研究进展，介绍了间隙模型在各个方面的应用情况，并提出了未来应该重点研究的关键技术问题。

赵阳等[2-3]分别以卫星天线双轴定位机构和含间隙四连杆机构为对象，研究了运动副间隙对机构运动特性的影响。王威等[4]以四杆机构为研究对象，研究了间隙和干摩擦同时存在对机构动力学性能的影响，研究表明间隙和干摩擦的存在会使机构的动力学性能产生不稳定现象，而且当系统启动初期或运动状态改变时影响更为剧烈。王旭鹏等[5]提出了一种修正的库伦摩擦模型，并以曲柄滑块机构为研究对象，研究了不同间隙、驱动载荷及摩擦因数对机构动力学性能的影响。孟凡刚等[6]建立了一种含间隙旋转副的碰撞铰模型，研究了不同的间隙、销轴半径、接触面的摩擦因数对机构动力学特性的影响，结果表明这些因素均能影响其动力学性能，且间隙对其影响最大。上述文献研究的内容主要是考虑间隙、摩擦和载荷等因素对机构动力学性能的影响，并没有考虑重力等因素对机构动力学性能的影响。

屈盛官等[7]研究了不同重力环境对空间机构铰链关节磨损的影响，研究表明间隙和重力都对轴承磨损有很大的影响。刘福才等[8]对不同重力环境下含间隙旋转铰的位置特性进行了仿真研究，通过建立连续接触等效模型，运用ADAMS软件仿真得到了不同重力下间隙对旋转铰运动状态的影响。上述文献作者在研究重力因素对含间隙机构的影响时，都只是考虑在微重力或不同重力的情况下间隙对机构的影响作用，并未研究不同重力环境下其他因素对机构的影响。

综上所述，许多学者根据微观接触理论建立微凸体的接触模型时，往往只考虑了法向接触刚度，未考虑微凸体变形过程中的弹塑性变形阶段，从而忽略了法向接触阻尼对碰撞力模型的影响。本文基于分形理论、L-N模型及宏微理论，建立了修正的接触刚度系数模型；同时考虑宏观的关节间摩擦和微观微凸体间的阻尼因素，采用指数函数的微凸体的变形阶段模型，建立了修正的法向接触阻尼模型；进而得到了新的含间隙旋转运动副元素间接触碰撞力模型，并通过试验验证了新模型的正确性。基于此模型，对不同重力下的含间隙铰链接触碰撞力特性进行了研究，采用单一因素影响试验法，分别研究了转速、间隙、不同重力环境以及表面粗糙度对含间隙铰链接触碰撞力的影响，为空间机构的本体结构设计和试验研究提供了理论依据和参考。

1 建立含间隙旋转副接触碰撞力模型

1.1 修正接触刚度系数

基于M-B分形理论，运动副接触表面微凸体的分布函数n(a′)和真实接触面积Ar可分别表示为[9]

(1)

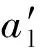
φ的关系式可以表示为

(2)

微凸体发生弹性变形的临界压缩深度ωc及临界接触面积a′c为

(3)

式中：kμ为摩擦力修正系数，kμ=1-0.288μ，(0≤μ≤0.3)，kμ=0.932e-1.58(μ-0.3)，(0.3<μ≤0.9)；Ф=σ/E*为材料的特征参数，σ为材料的屈服强度，E*为复合弹性模量；R为微凸体的曲率半径；G为尺度系数，与表面粗糙程度有关；γ为大于1的常数，通常取值为1.5。

(4)

(5)

式中：μ为动摩擦因数；E1，E2分别为两接触微凸体的弹性模量；v1，v2为两接触微凸体的泊松比；R1为轴套半径；R2为轴的半径。

接触变形阶段[10]分为弹性变形阶段、弹塑性变形阶段第一阶段、弹塑性变形阶段第二阶段、塑性变形阶段。微凸体的总接触刚度Km可由接触碰撞力增量dP与变形量dω的比值分别计算出弹性变形阶段的接触刚度Kn、弹塑性变形第一阶段的接触刚度Kn1、弹塑性变形第二阶段的接触刚度Kn2。

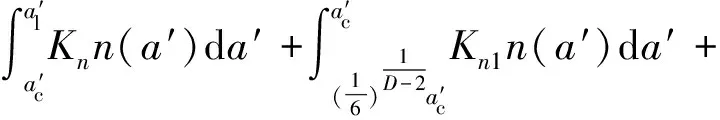
(6)

式中：h1,h2,h3,h4,m的表达式分别为

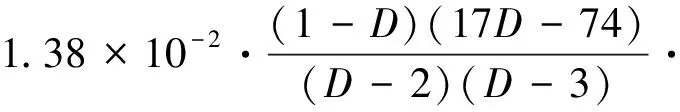
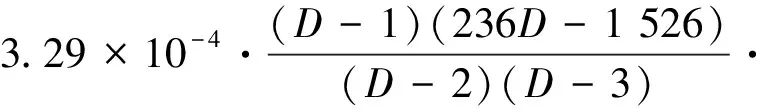
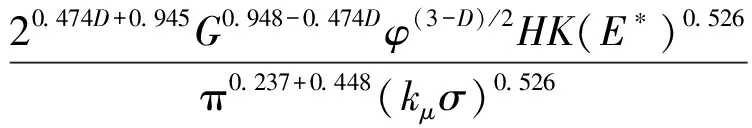
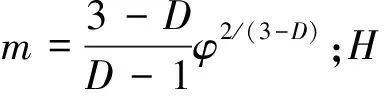
根据改进的Winkle模型，建立修正的接触刚度系数模型，如式(7)所示。

h2·Ψ(D-1)+h3·h4·Ψ(D-1)

(7)

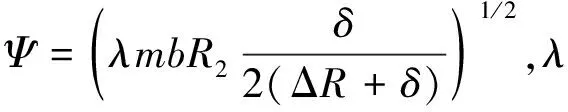
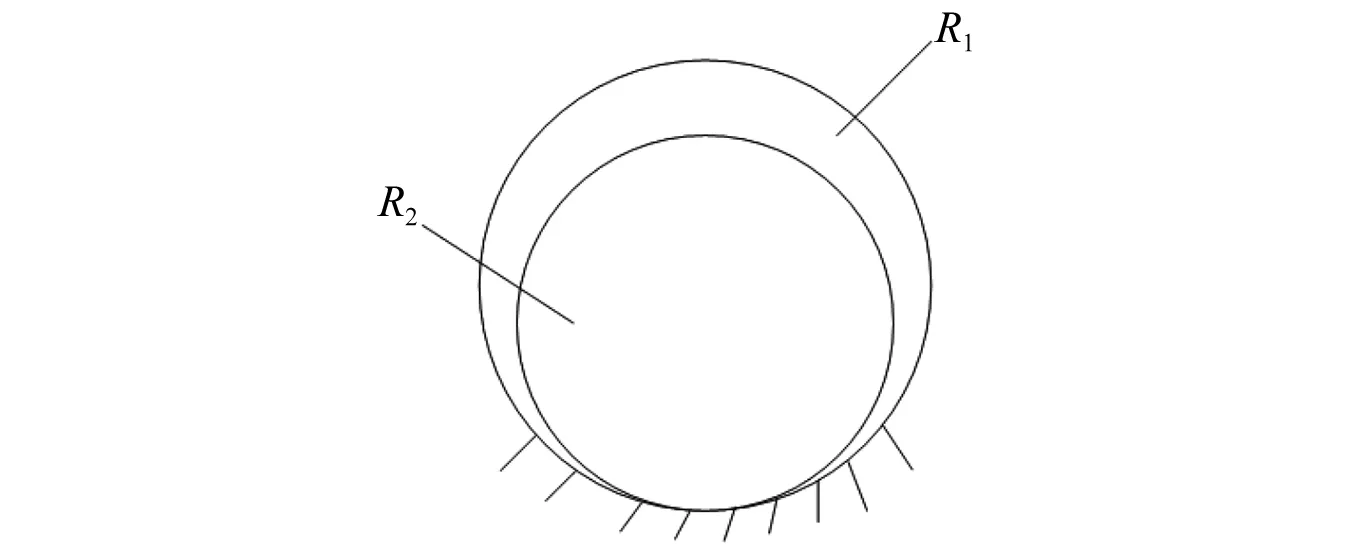
图1 轴和轴套间接触模型Fig.1 Contact model between shaft and sleeve

从式(7)可以得到，接触刚度Km是随实际接触面积Ar变化的，由实际接触面积Ar应小于名义接触面积A，设面积比例系数λ<1，令Ar=λA。

(8)

分形维数D和分形尺度参数G的计算公式为

(9)

G=10-5.26/Ra0.045

(10)

式中：Ra为表面粗糙度值，由实际工况确定。

1.2 修正阻尼系数

根据Hertz接触理论[11]，可以求得各个阶段微凸体的法向载荷，采用指数函数的微凸体的变形阶段[12-13]模型，考虑微凸体在变形的过程微凸体在弹性变形时将能量转化为弹性势能，发生塑性变形时能量将会损耗，进而通过积分可以算得微凸体的弹性势能和能量损耗。

(1)弹性变形阶段：

微凸体的法向载荷Pe为

(11)

微凸体弹性变形阶段的势能为

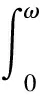
(12)

(2)弹塑性变化阶段：

当ωc≤ω≤110ωc时，微凸体发生弹塑性变形，此阶段的变形分为弹塑性变形第一阶段(ωc≤ω≤6ωc)和弹塑性变形第二阶段(6ωc<ω≤110ωc)。

弹塑性变形第一阶段，微凸体的法向载荷Pep1为

(13)

微凸体弹塑性第一阶段的势能为

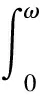
(14)

弹塑性变形第二阶段，微凸体的法向载荷Pep2为

(15)

微凸体弹塑性第二阶段的能量损失为

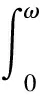
(16)

(3)塑性变形阶段：

当ω>110ωc时，微凸体发生塑性变形，此时法向载荷Pp为

Pp=2πωRH

(17)

塑性变形阶段的能量损失为

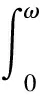
(18)

由微凸体的分布函数可以求得接触表面总的弹性势能为

(19)

接触表面总的能量损失为

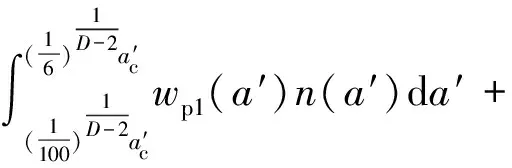
(20)

阻尼因子η可以表示为

(21)

设定粗糙表面所在基体质量[14]为M，则微凸体法向阻尼系数Cn为

(22)

修正的阻尼系数Dm可以表示为

Dm=Dn+Cn

(23)

式中，Dn为阻尼系数，其表达式为

(24)

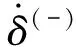
1.3 含间隙旋转副接触碰撞力模型

本文在文献[15]的基础上考虑摩擦和修正阻尼系数，得到了新的含间隙旋转运动副元素间接触碰撞力模型，如式(25)所示

(25)

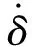
对含间隙机构采用Ambrósio[16]提出的改进库伦摩擦力模型，其模型表达式为

(26)

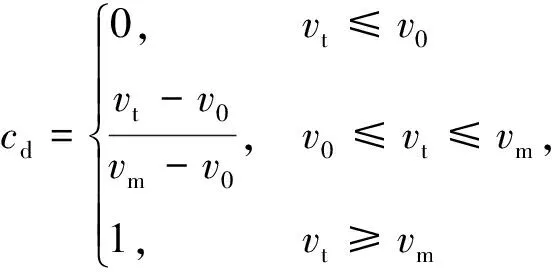
本文利用新的含间隙旋转副接触碰撞力模型，并以单铰链机构动力学模型[17]为研究对象，采用单一因素试验对含间隙铰链接触碰撞力特性进行了研究。

2 试验验证

为了进一步验证本文得到的接触力模型的正确性，将文献[18]中碰撞试验的初始条件应用到本文的模型中，利用自主设计的如图2所示的碰撞试验台，进行了试验研究。

图2 碰撞试验平台Fig.2 Collision experimental platform

试验台的具体参数如下：弹性模量为207 GPa，泊松比为0.3，表面粗糙度值Ra<6.3，等效质量为0.8 kg，间隙取值0.5 mm，恢复系数为0.46，通过试验得到了试验台的实际碰撞力。如图3所示，将新模型和修正模型的理论值分别与实测力进行了对比，数据表明修正模型的标准方差为6.14%，而新模型的标准方差为4.65%，两模型相差1.49%。根据Li等的研究结果以及上述分析可知，本文建立的法向接触力模型所得到理论数据与试验数据更加接近，这说明本文所建立的考虑摩擦和阻尼的法向接触力模型是正确的。

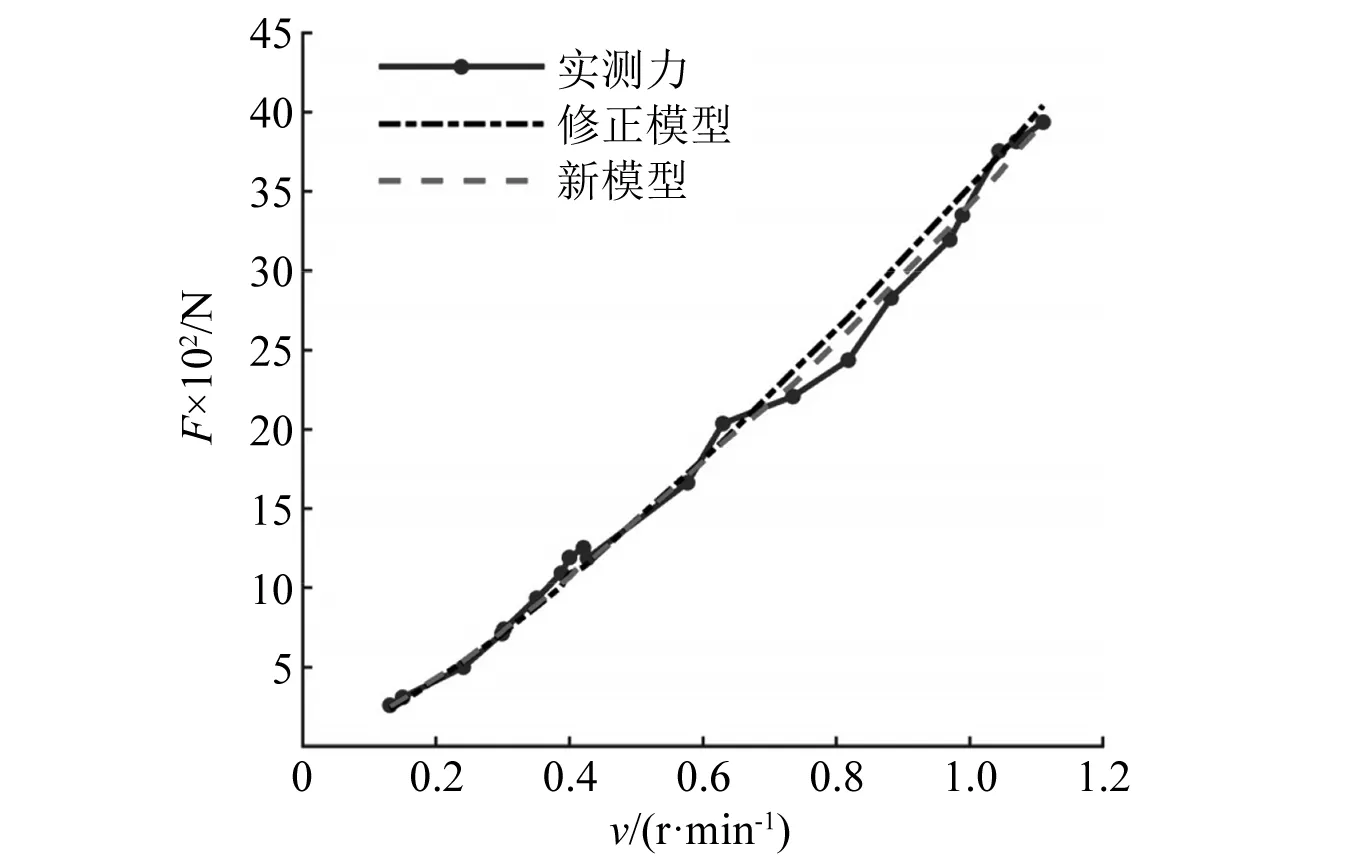
图3 新模型与修正模型数据对比图Fig.3 Data comparison between new model and modified model

3 单一因素试验

3.1 各个因素范围的选取

为了考虑多种因素对模型的影响，本文给出了新的算例，相关参数如下：轴与轴套直径的公称尺寸为10 mm，采用基孔制配合，通过改变轴的直径大小来调节二者之间的间隙值大小，轴与轴套的有效接触长度为10 mm，轴和轴套采用相同的材料，弹性模量为207 GPa，泊松比为0.3，恢复系数为0.9。

根据空间机构加工、装配精度、实际工作环境及刘福才等和Li等的研究成果，本文对不同重力加速度(g)情况下的旋转运动副元素间的间隙(c)、转速(v)及表面粗糙度(Ra)四种因素进行研究。重力加速度g取9.8 kg·m/s2，重力加速度的取值范围在0～1g；间隙c的取值为0.001～0.1 mm；确定转速v的选取范围[19]为5～100 r/min；根据零件表面实际加工精度，表面粗糙度Ra值的范围选取为0.4～6.3 μm。在进行单一因素影响试验时，为了减少试验次数，故选取各个因素为取值范围的中间数值，通过单一因素的数值变化进行试验。当重力加速度g为非主要试验因素时，对于重力加速度的取值，分别选取了有、无重力加速度两种情况进行了分析。

3.2 不同转速对法向接触力的影响试验

间隙取值为0.05 mm，表面粗糙度Ra取值为1.6 μm，重力加速度分别取值为0和1g，转速分别取值为5 r/min,25 r/min,50 r/min,75 r/min,100 r/min。通过仿真试验，分别得到了有、无重力加速度两种情况下，不同转速下的最大法向接触碰撞力，如图4所示。

由图4可以得到，在相同转速作用下，有、无重力加速度对试验结果的影响作用较大，重力下的法向接触碰撞力要大于微重力下的法向接触碰撞力，特别是在转速较低的情况下最为明显，随着转速的增加，二者的差值逐渐减小。在微重力情况下，随着转速的不断增加，旋转副副元素间法向接触碰撞力也逐渐增大，增长速度较为均匀，接近线性关系。但是在重力情况下，转速较低时，转速对旋转运动副元素间的法向接触碰撞力的影响很小，而随着转速的增加，法向接触碰撞力的变化率逐渐增大。

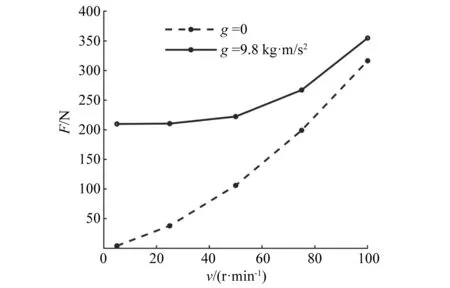
图4 不同转速对法向接触力的影响Fig.4 Effect of different rotational speed on force

3.3 不同重力加速度对法向接触力的影响试验

转速取值为50 r/min，间隙取值为0.05 mm，表面粗糙度Ra取值为1.6 μm，重力加速度分别取值为0,0.25g,0.5g,0.75g,1g。通过仿真试验，得到了不同重力加速度下的最大法向接触碰撞力，如图5所示。

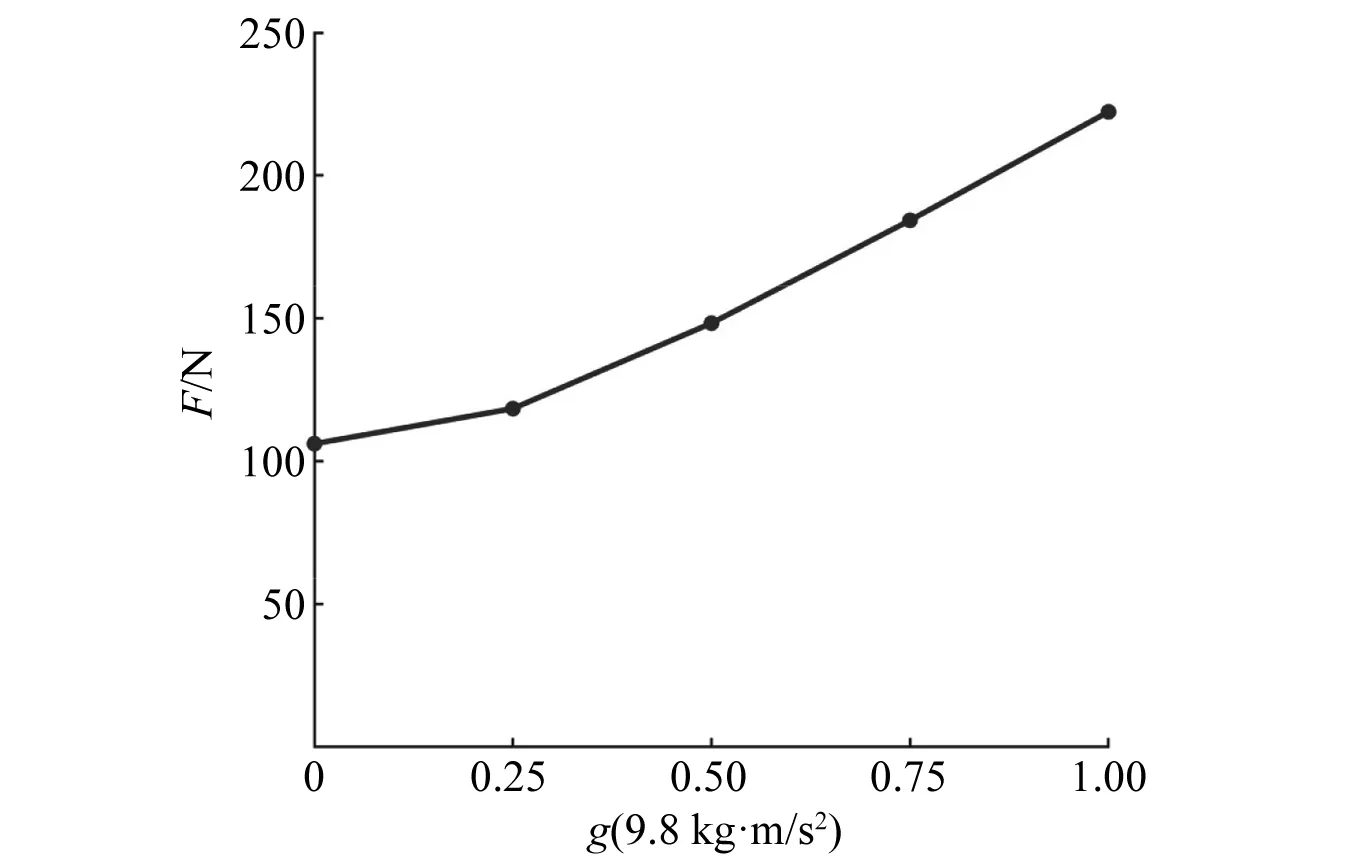
图5 不同重力加速度对法向接触力的影响Fig.5 Effect of different gravity acceleration on force

由图5可以得到，在微重力下(0～0.25g)，重力加速度对旋转运动副元素间的最大法向接触碰撞力影响作用较小。随着重力加速度的增加，最大法向接触碰撞力与重力加速度接近线性关系，这表明重力加速度的大小对试验结果影响较大。

3.4 不同间隙对法向接触力的影响试验

转速取值为50 r/min，表面粗糙度Ra取值为1.6 μm，重力加速度分别取值为0和1g，间隙分别取值为0.001 mm,0.025 mm,0.05 mm,0.075 mm,0.1 mm。通过仿真试验，分别得到了有、无重力加速度两种情况下，不同间隙下的最大法向接触碰撞力，如图6所示。

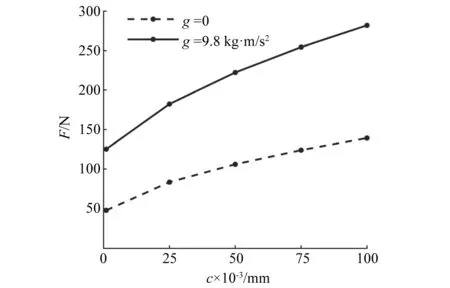
图6 不同间隙对法向接触力的影响Fig.6 Effect of different clearance on force

由图6可以得到，在具有相同间隙的情况下，重力下的最大法向接触碰撞力要比微重力下大。有、无重力加速度两种情况下，最大法向接触碰撞力的变化都是随着间隙值的增加而增加，结果与文献[20]是一致的。随着间隙值的增加，最大法向接触碰撞力增加速率逐渐变缓，且间隙值越大，两种情况下的碰撞力的差值就越大。

3.5 不同表面粗糙度对法向接触力的影响试验

转速取值为50 r/min，间隙取值为0.05 mm，重力加速度分别取值为0和1g，表面粗糙度Ra分别取值为0.4 μm,0.8 μm,1.6 μm,3.2 μm,6.3 μm。通过仿真试验，分别得到有、无重力加速度两种情况下，不同表面粗糙度下的最大法向接触碰撞力，如图7所示。

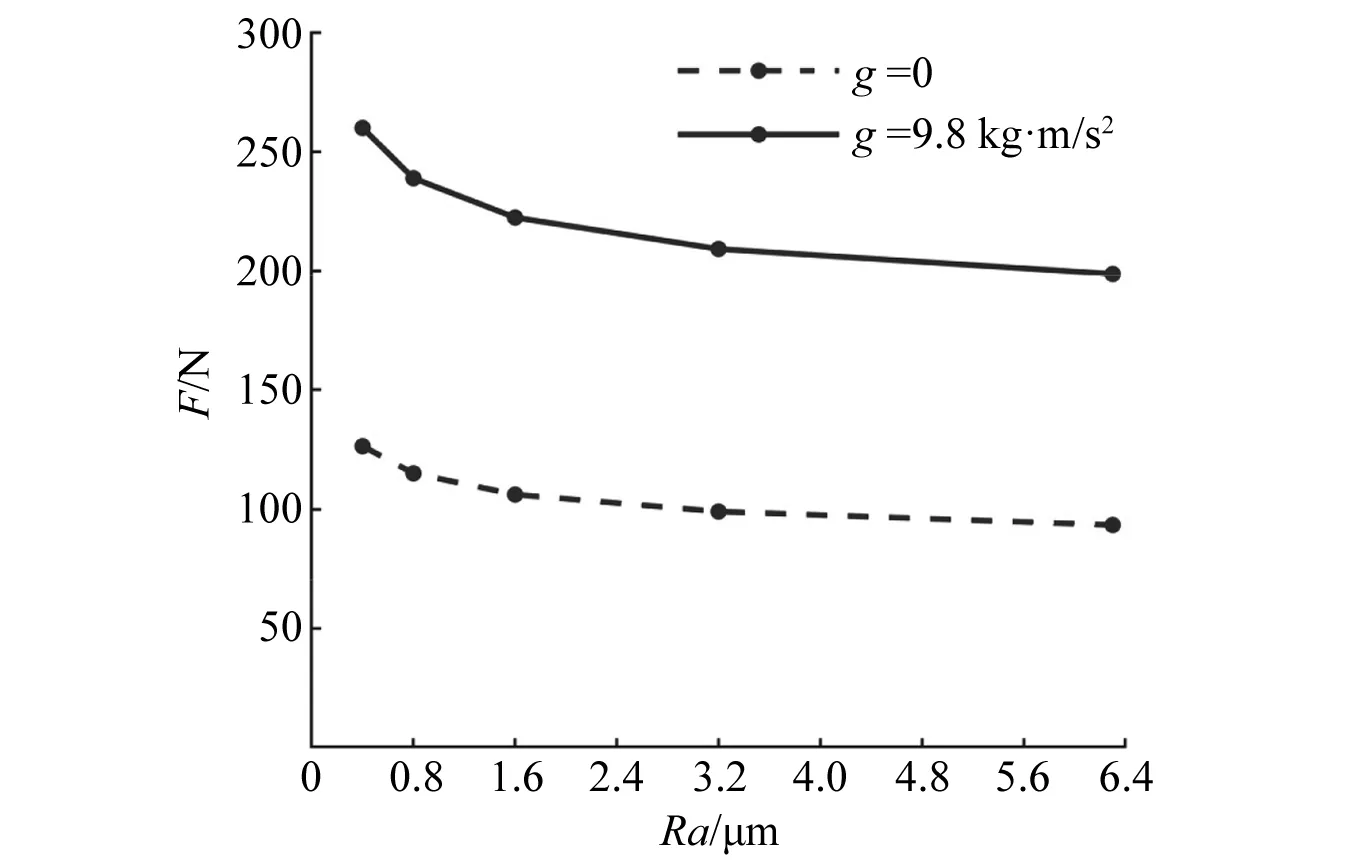
图7 不同表面粗糙度值对碰撞力的影响Fig.7 Effect of different surface roughness on force

由图7可以得到，无论是否存在重力，组成旋转副的两构件表面越粗糙(即表面粗糙度Ra值越大)，最大法向接触碰撞力越小。尤其在表面粗糙度Ra值小于0.8 μm时最为明显，结果与Whitehouse等的研究是一致的。随着表面粗糙度Ra值增大，表面粗糙度因素对最大法向接触碰撞力的影响作用逐渐减小，曲线趋于平缓。随着Ra值的变化，重力下的最大法向接触碰撞力与微重力下的最大法向接触碰撞力的差值大致是相同的，曲线走势基本相同。

通过分析不同因素的单一影响试验结果，可以得出：当重力加速度为非主要考虑因素时，有、无重力加速度两种情况下，该模型在重力下的最大法向接触碰撞力总是大于在微重力下的最大法向接触碰撞力的；其中转速、重力加速度和间隙三种因素对最大法向接触碰撞力的影响相对于表面粗糙度值对模型的影响是较大的。

4 结 论

本文基于分形理论、L-N模型及宏微理论，考虑宏观摩擦和微观阻尼因素，得到了新的含间隙旋转运动副元素间接触碰撞力模型。并基于此模型，以单铰链机构动力学模型为研究对象，通过单一因素影响试验法对空间机构的力学性能进行了研究，得出了以下结论：

(1) 在转速较低的情况下，重力大小对试验结果的影响较大，特别是在微重力下，法向接触碰撞力与转速呈近线性关系。

(2) 法向接触碰撞力随着间隙值的增大而增加，而且间隙值越大，在重力和微重力两种环境下的法向接触碰撞力的差值越大。

(3) 无论是否存在重力，旋转副副元素间表面粗糙度值越大，最大法向接触碰撞力越小，尤其是在表面粗糙度值小于0.8 μm时最为明显。

本文通过新建立的接触碰撞力模型和上述研究结论，可以为空间机构的设计、应用及可靠性分析提供了一种参考。