变工况下滚动轴承保持架碰撞接触动力学特性分析

涂文兵， 梁 杰， 杨锦雯， 杨本梦， 张桂源， 袁晓文

(1. 华东交通大学 机电与车辆工程学院，南昌 330013; 2. 华东交通大学 轨道交通基础设施性能监测与保障国家重点实验室，南昌 330013)

保持架作为约束和引导滚动体运动的重要组成元件，工作时与滚动体间的碰撞和摩擦作用直接地影响到自身、甚至是整个轴承的工作性能。为此，分析保持架动力学特性，准确把握滚动体与保持架之间碰撞接触的产生及变化机理，对于消除和控制破坏性碰撞，减少保持架失效、改善轴承性能、延长轴承寿命等具有十分重要的意义。

Kakuta[1]最早从理论上分析了球轴承滚动体对保持架接触作用力的产生机理，并从试验方面研究了套圈不对中对作用于保持架上冲击力的影响。Walters[2]建立了六自由度保持架的深沟球轴承动力学模型，首次通过数值仿真研究了保持架的瞬态运动特性，为滚动轴承保持架接触动力学研究奠定了良好的基础。Gupta[3]考虑各轴承部件完全自由度建立了滚动轴承动力学模型，深入研究了保持架的运动机理，并分析了滚动体与保持架之间接触作用力对保持架运动稳定性的影响。Rivera[4]在Gupta的基础上忽略几何因素的影响建立了简化的轴承动力学模型，并分析了保持架的运动稳定性，研究结果表明保持架不稳定运动的产生原因主要是滚动体与保持架相互的接触作用，然而，模型中对滚动体与保持架间接触行为的处理方式较为简单，无法准确反映两者之间的真实接触状况变化。胡于进等[5]将滚动体与保持架之间的接触考虑为流体动力润滑、刚性接触和自由接触三种状态，建立了相应的数值计算模型，研究并分析了保持架运转过程中接触状态的变化规律及兜孔间隙和润滑油性质对接触作用力的影响。Meeks等[6]在通过拟静力学方法确定轴承内部载荷分布的基础上，采用非完全线性接触方式处理了滚动体与保持架之间的接触，研究了摩擦因数和轴承间隙对保持架磨损和所受接触力的影响。Boesiger等[7]考虑保持架弯曲和接触区域局部弹性变形研究了保持架兜孔的受力及保持架的动态特性。陈国定等[8]考虑表面粗糙度效应下具体分析了运动过程中滚动体与保持架之间相互作用力随滚动体位置角的变化规律。赖拥军等[9]考虑保持架兜孔间隙的影响，分析了稳定工况下多个保持架兜孔的受力情况，并得出保持架疲劳失效的重要原因之一是滚动体产生的高频碰撞冲击。自此，许多学者对保持架与滚动体之间的碰撞接触特性展开了大量的研究。周延泽等[10]采用简化的质点-杆、质点-固支梁系统模拟滚动体与保持架横梁、侧梁的局部接触，研究了理想状态下球与保持架碰撞瞬时的冲击载荷变化及其影响因素。刘文秀等[11]通过模糊碰撞理论定义了滚动体与保持架碰撞接触的发生条件，并建立了保持架的动力学分析模型，从运动稳定性方面探究了结构参数对保持架与滚动体之间碰撞力的影响规律。王春洁等[12]建立了静止滚动体与保持架的冲击振动模型，研究了不同偏斜角、转速及静载荷条件下保持架冲击载荷的变化规律。姚譞[13]突出考虑保持架与滚动体间的碰撞作用，将滚动体与保持架简化为相互作用的不连续碰撞振动系统，并分析了不同工况条件下保持架所受碰撞力的变化特性。保持架碰撞接触特性已越来越成为滚动轴承性能分析的重要前提。

随着滚动轴承向着高速、重载、精密等方向发展，保持架失效现象愈发明显，针对保持架在变速、变加速、变载荷等典型复杂变工况下的动态接触特性研究已成为当下亟待解决的热点问题。崔立等[14]基于拟动力学计算结果建立了球轴承滚动体/保持架有限元模型，分析了滚动体碰撞作用下保持架的动态特性变化及应力分布特点，指出工况的突变和结构参数的不合理均会导致保持架承受较大的碰撞应力。张娟等[15]利用ADMAS软件分析了主轴轴承在风机启动至平稳运行、转速突变及紧急制动三种特殊工况下滚动体与保持架之间接触力幅值、平均值等特性参数的变化。李红涛等[16]充分考虑滚动体与保持架横梁之间润滑状态的改变，计算分析了停止阶段任意时刻滚动体与保持架间的碰撞力变化，并建立了滚动体与保持架的有限元接触模型，研究了角加速度、外载荷、润滑油、保持架材料及结构尺寸对保持架应力分布的影响规律。涂文兵等[17]、罗丫等[18]分别研究了加、减速非平稳工况下外载荷和角加速度对角接触球轴承保持架运动以及单个滚动体与保持架碰撞力的影响，并结合试验进行了验证。刘乐平等[19]运用ANSYS/ LS-DYNA研究了简谐转速波动工况下不同波动频率和幅值对圆柱滚子轴承滚动体与保持架之间接触碰撞程度的影响规律。

以上研究成果从不同角度出发对滚动轴承运转过程中保持架的碰撞接触特性展开了分析，并且探究了不同因素对碰撞接触程度和变化过程的影响规律。但研究主要集中在平稳工况，分析模型中大多忽略了滚动轴承运动部件的动态效应。然而，滚动轴承运动部件的动态效应将对保持架的碰撞接触及其性能产生重要作用，尤其在非稳定工况下。此外，虽然部分学者在变工况下保持架动态接触特性方面的研究取得了一些成果，但未涉及不同变工况影响程度的对比研究，且由于主要采用ANSYS、ADMAS等软件进行仿真模拟，不能较好地描述滚动体与保持架之间的相互碰撞和摩擦问题。因此，本文采用动力学分析方法，考虑滚动体离心力与重力、内圈(含转子)和滚动体的动态效应等，建立了滚动轴承动力学分析模型，重点针对匀、加、减速及不同转速波动工况下的滚动体与保持架间碰撞力幅值、次数及分布变化情况进行了对比分析。旨在揭示保持架失效和工况特征之间的关系，从而为工况的合理选取以及保持架结构的改进设计提供参考。

1 滚动轴承动力学模型

滚动轴承运动部件的动态效应会直接导致滚动体与套圈之间接触位置角的改变，且兜孔间隙的存在使实际工作过程中滚动体与保持架之间的接触状态和接触关系十分复杂。为便于建立滚动轴承动力学模型，引入内圈(含转子)及滚动体动态效应对保持架碰撞冲击作用的影响，本文假设轴承系统中各元件均为刚体，质心与几何中心重合，并且运动仅局限于轴承平面内，假定外圈固定，不考虑保持架与套圈挡边之间的流体动压作用，忽略保持架质心的平动自由度。

此外，准确处理和计算轴承各组成元件之间的相互作用是保持架接触特性研究的重要基础和关键。为此，本文考虑润滑等非线性因素影响，采用非完全弹性碰撞力模型的接触力计算方法[20]，将保持架兜孔与滚动体之间的碰撞接触考虑为弹簧刚度和阻尼的等效作用，并通过设定合理的摩擦因数来计算摩擦力的大小，而滚动体与套圈之间的接触作用则通过Hertz弹性接触和牵引-润滑模型[21]来模拟，如图1所示。ωaj，ωbj，ωc分别为第j个滚动体公转角速度、自转角速度及保持架角速度。

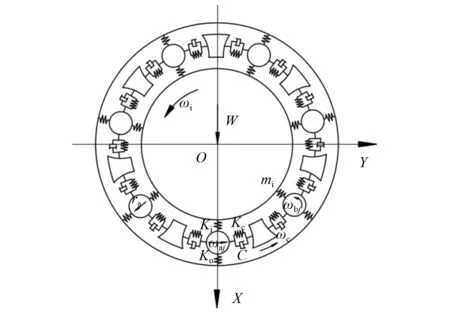
图1 滚动轴承动力学模型Fig.1 Dynamic model of rolling bearing

1.1 滚动体与套圈间的相互作用

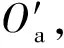
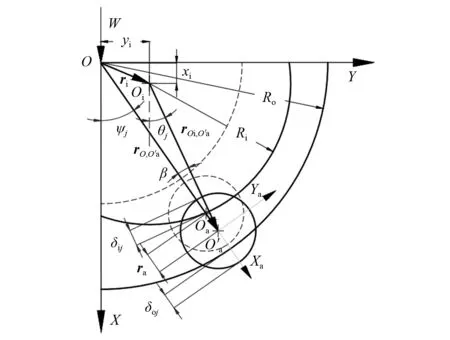
图2 滚动体与套圈之间的位置关系Fig.2 Position relationship between the roller and the ring

考虑轴承径向游隙，第j个滚动体与内圈的接触变形可表示为

(1)

(2)

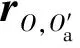
(3)

式中，rO,Oa为滚动体中心初始位置(Oa)在惯性坐标系下的位置矢量。

滚动体与外圈的接触变形取决于滚动体的径向位移和径向游隙，可表示为

(4)

根据Hertz接触理论可知，第j个滚动体与内、外圈间的接触力大小可表示为[22]

(5)

式中：Ki和Ko分别为滚动体与内、外圈间的接触刚度系数，详细计算过程见文献[23-24];n为滚动体与内、外圈滚道间的接触系数，对于球轴承，n取1.5。

根据库伦摩擦定律可知，摩擦力为摩擦因数和接触面间法向力的乘积。因此，滚动体与内、外圈滚道之间的摩擦力大小可表示为

(6)

式中，μ为滚动体与内、外圈滚道之间的牵引润滑摩擦因数，随相对滑动速度ΔV的改变而改变，相关计算方法可参考文献[25]。

1.2 滚动体与保持架之间的相互作用力

为较为真实地反映滚动体与保持架兜孔之间的动态接触关系，考虑间隙碰撞和润滑摩擦作用，建立保持架兜孔坐标系OpXpYp来计算滚动体与保持架兜孔之间的弹性变形量δcj。图3为任一角位置Ψj处滚动体与保持架之间的位置关系，Op为保持架兜孔中心，Xp，Yp分别为保持架的径向方向和圆周方向。

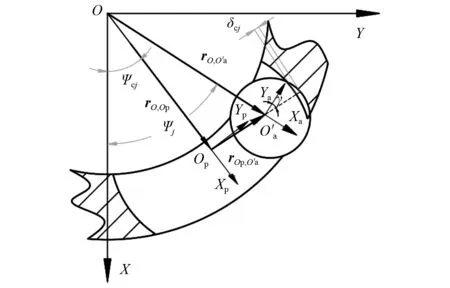
图3 滚动体与保持架之间的位置关系Fig.3 Position relationship between roller and cage

由图3可知，只有当δcj>0时，滚动体与保持架发生接触，反之，两者脱离接触，无接触变形。考虑保持架兜孔间隙，第j个滚动体与保持架兜孔之间的接触变形可表示为

(7)

(8)

式中，rO, Op为保持架兜孔中心(Op)在惯性坐标系下的位置矢量。

因此，第j个滚动体与保持架兜孔之间碰撞力、摩擦力的大小分别为[26]

(9)

Fcj=μcNcj

(10)

式中：Kc为滚动体与保持架之间的等效接触刚度系数；C为等效接触阻尼系数；Vcj为接触点法向相对速度；μc为摩擦因数，由于滚动体与保持架之间的相对滑移速度较大，故取为常数。

1.3 非线性动力学微分方程组

保持架设计为滚动体引导，在运动过程中，内、外圈对保持架的作用力为零，并且由于滚动体与保持架兜孔前端、后端接触时碰撞力的作用效果也会不同。因此，本文将滚动体分别与保持架兜孔前、后端接触时的碰撞力用Nc1j，Nc2j表示，摩擦力用Fc1j，Fc2j表示，包保持架受力示意图如图4所示。保持架的运动微分方程可表示为

图4 保持架受力示意图Fig.4 Schematic diagram of cage force

(11)

式中：Jc为保持架绕质心的转动惯性；Ψc为保持架转动角位移。

内圈的运动受到外加径向载荷、滚动体接触力及其相应摩擦力的直接影响，故内圈的运动微分方程可表示为

(12)

滚动体的运动微分方程可表示为

(13)

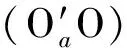
(14)

本文采用四阶定步长Runge-Kutta法对上述运动微分方程式(15)～式(18)联立进行积分求解，进而得到各瞬时轴承内部元件的受力分布和运动状态。综合考虑计算结果的收敛性和计算效率，初始积分步长设置为Δt=5×10-6s，计算过程流程如图5所示。

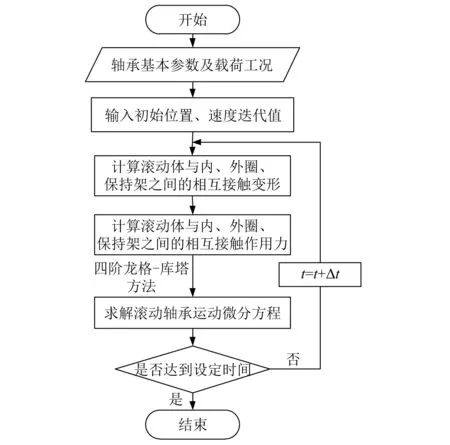
图5 计算过程流程图Fig.5 Calculation process flow chart

2 模型验证

本文选用6309型深沟球轴承为研究对象，相关尺寸参数如表1所示。由于径向载荷较大、内圈转速较低时，滚动轴承运动部件的动态效应较弱且打滑现象不明显，此时保持架运动基本上按照理论转速旋转。因此，分别针对内圈转速ωi=1 000 r/min时不同径向载荷(W=1 000 N，W=2 000 N，W=3 000 N)下滚动体与套圈的动态接触载荷分布、径向载荷W=3 000 N时不同内圈转速(ωi=1 000 r/min，ωi=2 000 r/min,ωi=3 000 r/min)下保持架转速仿真值(由于仿真过程初期保持架转速随时间变化幅度较大，故本文取仿真时间1～2 s内的保持架转速平均值作为该工况下的保持架转速仿真值)与静力学计算得出的解析结果、保持转速理论值进行对比，以验证所建动力学模型的有效性。对比结果如图6、表2、表3所示。

表3 径向载荷W=3 000 N时不同内圈转速下保持架运动参数对比Tab.3 Comparison of cage motion parameters under different inner ring speeds under radial load W=3 000 N

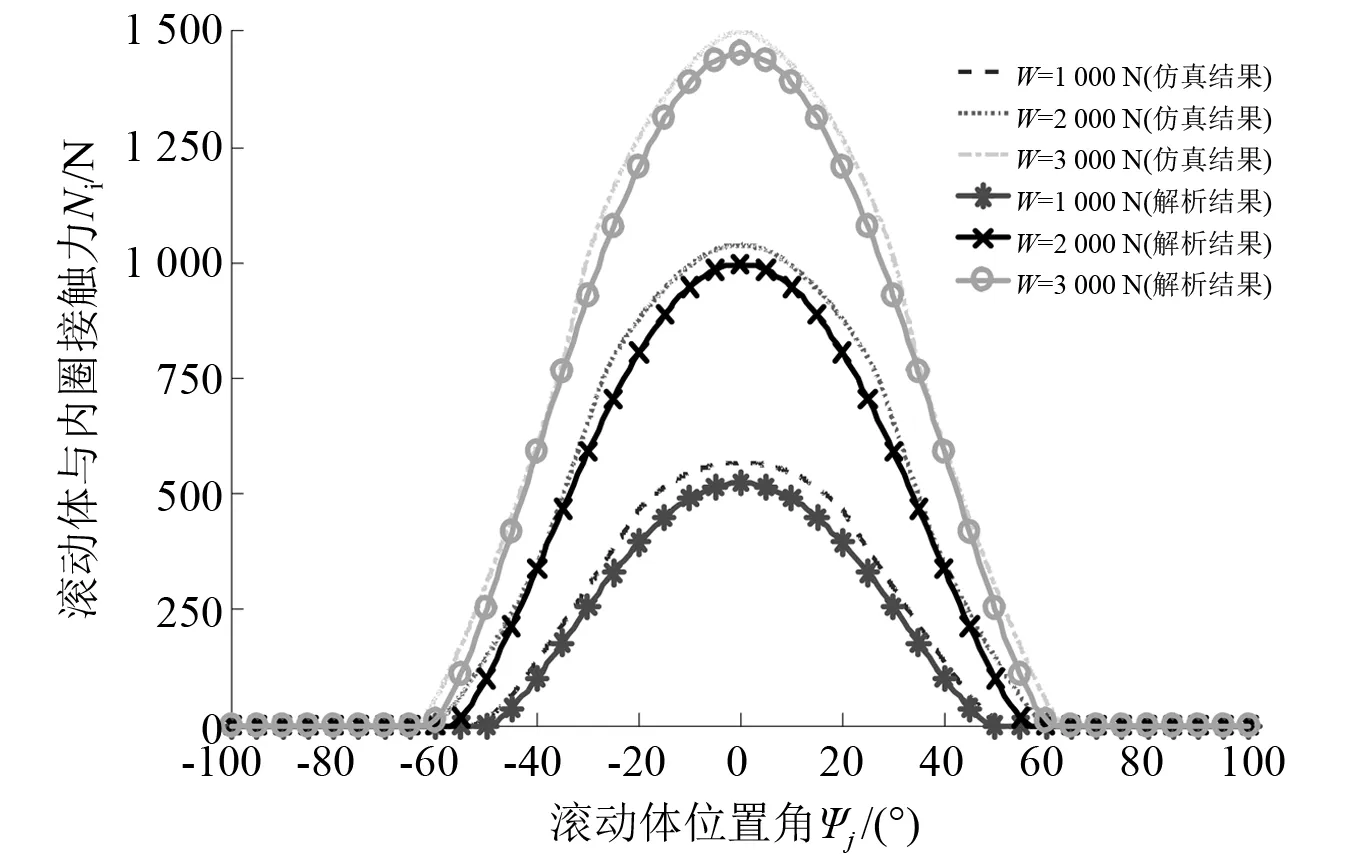
图6 内圈转速ωi=1 000 r/min时不同径向载荷下仿真和解析载荷分布曲线Fig.6 Simulation and analytical load distribution curves under different radial loads when inner ring speed ωi=1 000 r/min

表1 6309型深沟球轴承几何参数Tab.1 Geometric parameters of 6309 deep groove ball bearings

表2 内圈转速ωi=1 000 r/min时不同径向载荷下最大接触载荷对比Tab.2 Comparison of maximum contact loads under different radial loads when inner ring speed ωi=1 000 r/min

滚动轴承接触载荷的静力学计算公式为

(15)

式中，δr为Ψj=0°处套圈的径向移动量。

轴承外圈固定，内圈转动，保持架理论转速ωcm计算公式为

(16)

由图10、表2、表3可以看出，转速较低时，不同径向载荷作用下滚动体与套圈接触载荷分布曲线的仿真结果与解析结果相似，最大接触载荷仿真解与解析解近似相等，误差均在10%以下；内圈转速一定时，随着径向载荷的增加轴承运动部件的动态效应减弱，最大接触载荷仿真解与解析解之间的误差也越来越小；径向载荷较大时，不同内圈转速下保持架转速仿真值与理论值的误差均保持在0.3%上下。仿真结果与解析结果吻合较好，验证了本文所建立的轴承动力学模型的有效性，为本文后续的分析奠定了良好的基础。

3 分析结果与讨论

3.1 匀、加、减速工况下保持架碰撞接触特性分析

旋转机械的运动历程大致可以概括为启动、稳定运行、停车三个阶段。在启动和停车过程中，滚动轴承普遍具有较大的加速度，运动状态的急剧变化使滚动体与保持架之间的碰撞接触表现出一定的规律和区别。为进一步揭示其中的联系，本文基于所建模型模拟滚动轴承由零加速至一指定转速后保持一定时间的稳定转动，进而再减速至零的变化过程，对匀、加、减速工况下滚动体与保持架的碰撞接触特性展开对比分析。假设稳定运行时内圈转速ωi为300 rad/s，忽略润滑油密度和黏度的影响，将加、减速过程简化为理想的线性增加和线性减小，角加速度大小为300 rad/s2，内圈转速变化曲线如图7所示。

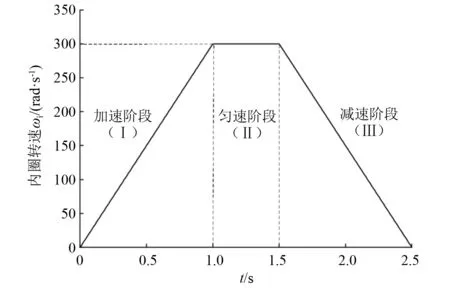
图7 内圈转速变化曲线Fig.7 Change curve of inner ring speed

由于各滚动体与保持架间相互作用力的变化趋势基本相同，在不失一般性的条件下，选择第一个滚动体与保持架之间的动态接触载荷变化进行了分析。考虑到需减小和控制其他因素对滚动体与保持架之间接触作用力的影响，径向载荷W设置为3 000 N。

保持架设计过程中我们首先需要考虑的是能否承受未来工作环境下可能出现的极限载荷，且由于不同工况下滚动体与保持架兜孔前、后端接触状态不同，故本文分别对上述运动过程中滚动体与保持架兜孔前、后端碰撞力的幅值变化进行了统计分析。图8为整个过程中滚动体与保持架兜孔碰撞力幅值随滚动体转动周期变化曲线图。

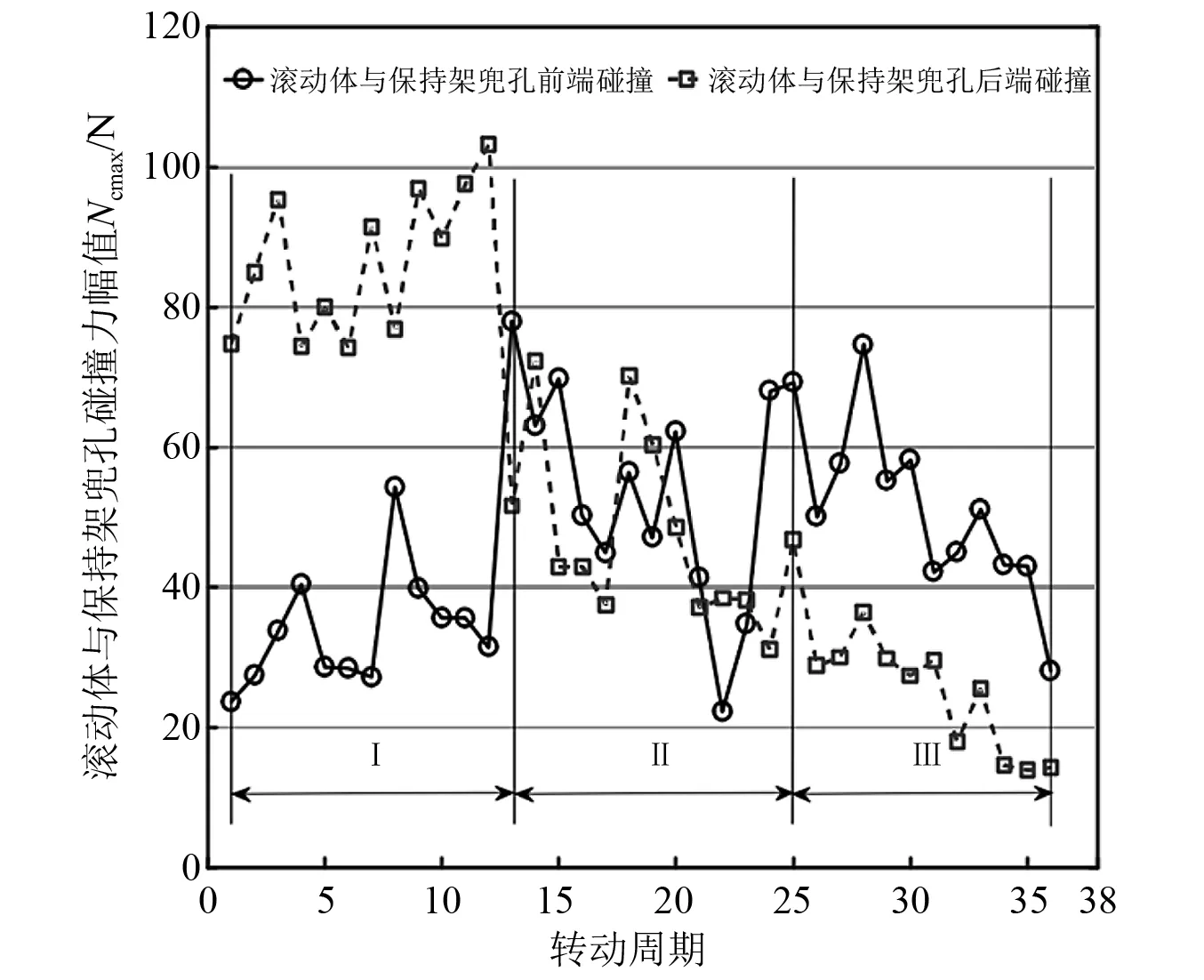
图8 滚动体与保持架兜孔碰撞力幅值随滚动体转动周期变化曲线图Fig.8 Curve of the amplitude of the impact force between the roller and the cage pocket changing with the rotation period of the roller

从图8可以看出，加速过程(Ⅰ)中，滚动体与保持架兜孔的前端碰撞力幅值呈明显的抖动上升趋势，而后端碰撞力幅值上升趋势不明显，前端碰撞力幅值的波动程度较后端更大，但碰撞力幅值明显小于后端碰撞力幅值。这可能是由于加速过程中保持架运动主要靠滚动体推动，滚动体与保持架兜孔前端始终保持比较紧密的接触(主要发生在承载区，见图9(a))，而后端的碰撞力主要是由于保持架和滚动体的不稳定运动造成的碰撞引起的(主要发生在非承载区，见图9(a))；匀速过程(Ⅱ)中，滚动体与保持架兜孔的前端碰撞力幅值相较于后端碰撞力幅值时大时小，碰撞不稳定，随机性较强，产生这种现象的原因可能是由于轴承内部运动元件存在较强的不稳定因素造成的；减速过程(Ⅲ)中，滚动体与保持架兜孔的碰撞力幅值基本呈抖动下降趋势，前端碰撞力幅值先减小、后增大，然后在震荡中逐渐降低。相较于前端碰撞力幅值，后端碰撞力幅值更小，这可能是由于减速过程中滚动体阻碍保持架的运动，与保持架兜孔后端接触较为紧密造成的(主要发生在承载区，见图9(c))。

图9 不同阶段下单个转动周期内滚动体与保持架兜孔碰撞力曲线图Fig.9 Curve of collision force between the roller and the cage pocket in a single rotation period at different stages

为更为直观地比较滚动体与保持架间碰撞接触特性的变化规律，表4给出了不同阶段内滚动体与保持架兜孔碰撞力幅值统计值。可以发现，由于不同变速工况下轴承内部元件受力、运动状态不同，加速阶段(Ⅰ)滚动体与保持架兜孔前端碰撞力幅值平均值相比于后端要小的多，减速阶段(Ⅲ)则相反；受变速过程的影响，相比于加(Ⅰ)、减速(Ⅲ)阶段，匀速阶段(Ⅱ)滚动体与保持架兜孔前、后端碰撞力幅值变化范围最大，碰撞力幅值平均值较高，说明此时滚动体和保持架之间碰撞程度较高，但随机性较强；整个运动过程中，滚动体与保持架兜孔前端碰撞力幅值变化范围相较于后端更大，这是由于滚动体与保持架兜孔前端碰撞力是维持保持架同向转动的主要作用来源，当滚动体运动状态受内圈不稳定运动的影响时，会直接造成对保持架兜孔前端碰撞力幅值的改变。因此，考虑滚动轴承运动元件动态效应影响在保持架动态接触特性分析中是必不可少的。

表4 不同阶段内滚动体与保持架兜孔碰撞力幅值统计值Tab.4 Amplitude statistics of the impact force between the roller and the cage pocket in different stages

图9给出了不同阶段下单个转动周期内滚动体与保持架兜孔碰撞力曲线图。从图9中可以看出，相较于匀速阶段(Ⅱ)，变速过程中滚动体与保持架间碰撞次数增多；加速(Ⅰ)时，处于承载区内的滚动体受到足够驱动作用力影响主要与保持架兜孔前端发生碰撞，非承载区内伴随着打滑现象和重力作用的明显，滚动体与保持架兜孔后端碰撞，且主要发生在非承载区前半段，如图9(a)所示；减速(Ⅲ)时，承载区内滚动体主要与保持架兜孔后端发生碰撞，而由于位置角的不同使重力的作用效果发生改变，在非承载区后半段滚动体与保持架兜孔前端发生频繁碰撞，如图9(c)所示。

3.2 不同转速波动工况下保持架碰撞接触特性分析

实际生产生活中，电机输出的驱动力矩会受到工作环境等外界因素的影响产生变化，且机械系统内部各中间构件变速运动时产生的惯性力矩更是会直接造成滚动轴承的运行转速出现不同形式的周期性波动，进而加剧滚动体与保持架之间的碰撞，加快保持架损坏[19]。为更加清楚地了解到不同转速波动工况下保持架是否仍然具有良好的动力学特性及不同转速波动工况条件对滚动体与保持架之间碰撞接触特性的影响变化，本文选取较为典型的周期性简谐波动、矩形波动、三角波动转速工况与稳定工况展开对比研究。假设转速波动周期均为0.02 s，内圈转速变化曲线如图10所示。

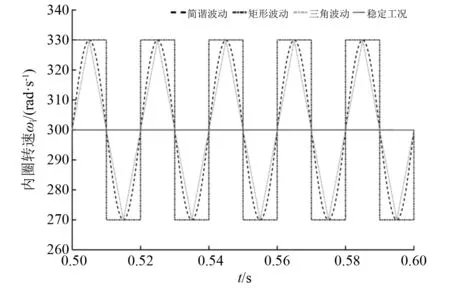
图10 内圈转速变化曲线Fig.10 Change curve of inner ring speed

图11、表5分别给出了不同工况下滚动体与保持架兜孔碰撞力幅值随滚动体转动周期变化曲线、滚动体与保持架兜孔碰撞力幅值统计值。通过对比可以看出，由于转动波动工况下滚动体、保持架的运动状态时刻发生改变，不稳定性较强，故两者之间的碰撞力幅值和平均值相较于稳定工况要大得多，且变化范围也较大；不同转速波动工况下滚动体与保持架碰撞剧烈程度不一样，碰撞最剧烈的是矩形波动工况，简谐波动工况次之，三角波动工况最小。这是由于不同转速波动下轴承内部运动元件的不稳定程度不同引起的，矩形波动工况下转速变化明显，滚动体和保持架的不稳定运动剧烈，碰撞作用力急剧增大。

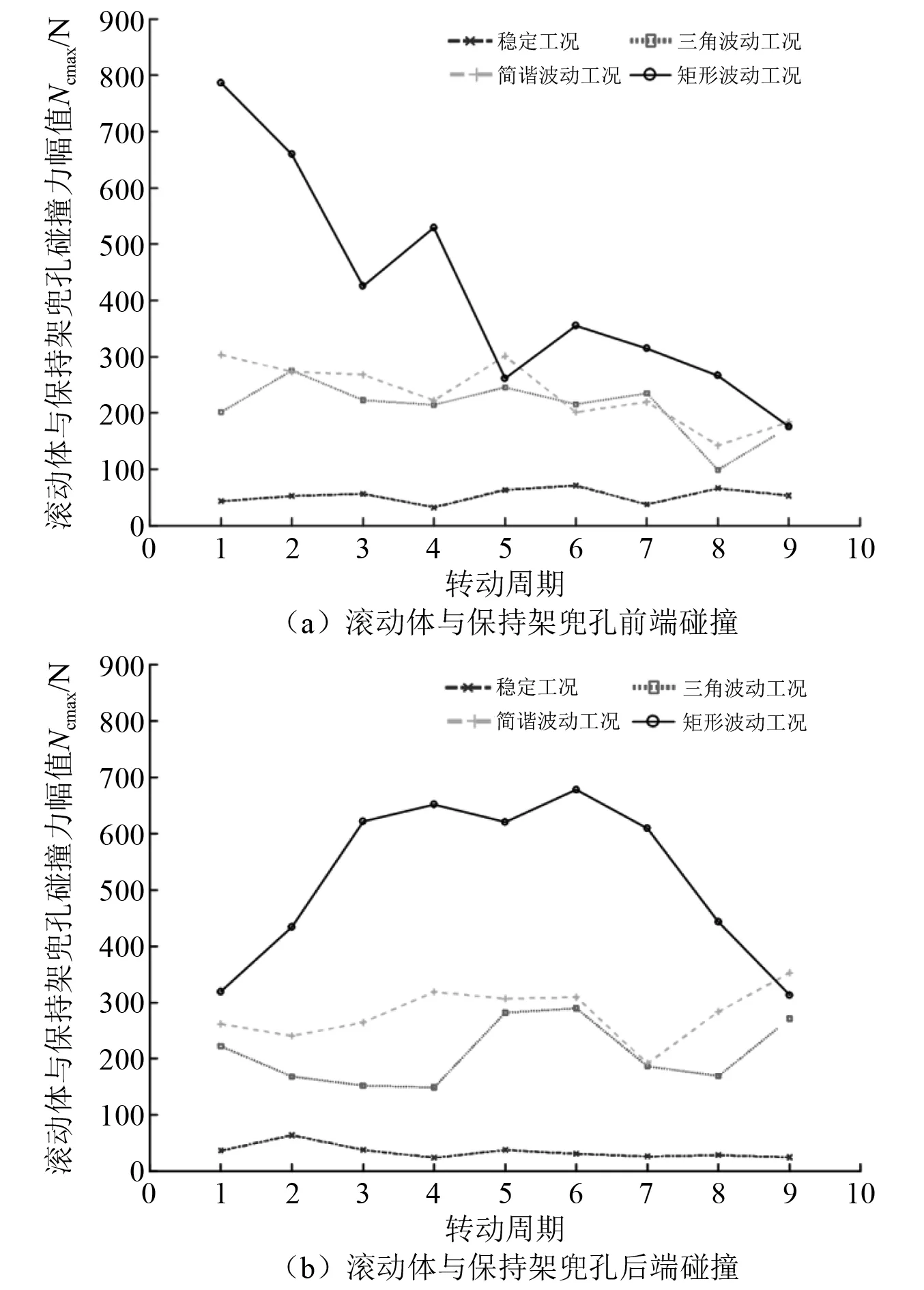
图11 不同工况下滚动体与保持架兜孔碰撞力幅值随转动周期变化曲线Fig.11 Curve of the amplitude of the impact force between the roller and the cage pocket as a function of the rotation period under different working conditions

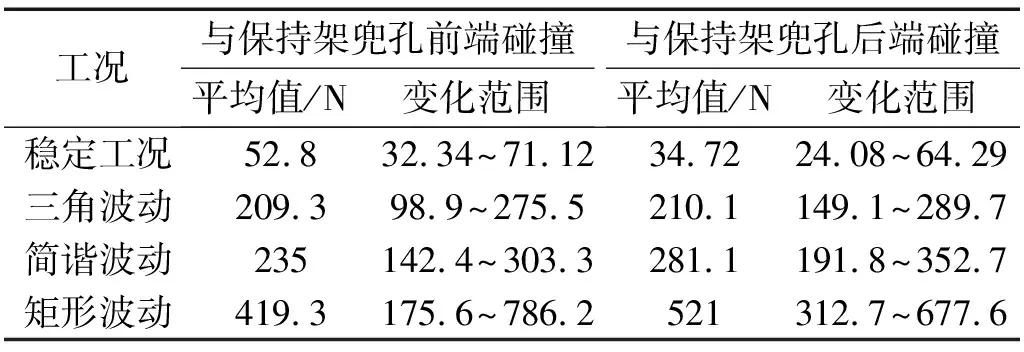
表5 不同工况下滚动体与保持架兜孔碰撞力幅值统计值Tab.5 Amplitude statistics of the impact force between the roller and the cage pocket under different working conditions

由于转速波动变化较快，不同滚动体转动周期内滚动体与保持架兜孔碰撞力分布无明显统一规律，故本文给出单个转速波动周期(0.9～0.92 s)内不同工况下滚动体与保持架兜孔碰撞力曲线图，分析不同转速波动工况对滚动体与保持架之间碰撞次数的影响，如图12所示。从图中可以看出，转速产生波动时滚动体与保持架兜孔之间的碰撞次数较稳定工况显著增加，但不同转速波动形式下碰撞次数不同，由少到多依次为三角波动、简谐波动、矩形波动。碰撞次数与碰撞程度的一一对应，说明了转速矩形波动工况下，保持架和滚动体之间的破坏性碰撞现象严重，对保持架和轴承性能造成的影响最大。

图12 不同工况下单个转速波动周期内滚动体与保持架兜孔碰撞力曲线图Fig.12 Curve of impact force between the roller and the cage pocket in single speed fluctuation cycle under different working conditions

4 结 论

本文以深沟球轴承6309为研究对象，建立了考虑滚动体与保持架碰撞接触的滚动轴承动力学模型，从碰撞力幅值、次数及分布情况等方面对滚动体与保持架之间的碰撞接触特性展开了分析，对比研究了不同变转速工况对保持架碰撞接触动力学特性的影响规律，主要结论如下：

(1)变速工况下滚动体与保持架间碰撞次数增多；加速工况下滚动体与保持架兜孔前端碰撞力幅值的波动程度较后端更大，但碰撞力幅值明显小于后端碰撞力幅值；减速工况下相较于后端碰撞力幅值，前端碰撞力幅值更大。

(2)加速工况下，滚动体在承载区内主要与保持架兜孔前端发生频繁碰撞，非承载内则主要与后端发生碰撞；减速工况下，滚动体与保持架兜孔前端碰撞主要发生在非承载区，而后端碰撞则主要发生在承载区。在对保持架结构强度和疲劳寿命进行校核计算时，应着重考虑启、停阶段时保持架所受冲击力的大小。

(3)相较于稳定工况，转速波动工况下滚动体与保持架间碰撞次数显著增加，且不同转速波动形式下碰撞剧烈程度不同，碰撞最剧烈的是矩形波动工况，简谐波动工况次之，三角波动工况最小。因此，轴承实际工作过程中需考虑改善轴承设计和工作环境条件，避免因输入转速波动对保持架带来严重后果，尤其避免转速周期性矩形波动的产生。