扁平流线型箱梁涡激振动雷诺数效应研究
刘庆宽, 任若松, 孙一飞, 李 震, 郑云飞
(1. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043;2. 河北省风工程和风能利用工程技术创新中心,石家庄 050043;3. 石家庄铁道大学 土木工程学院,石家庄 050043; 4. 石家庄铁路职业学院 铁道工程系,石家庄 050043)
风对桥梁的作用包括静力作用和动力作用,其中,动力作用主要是指颤振、驰振、涡激振动和抖振等风致振动,危害非常严重,受到广泛关注。涡激振动是一种发生在低风速下的常见振动,国内外许多桥梁都曾发生过明显的涡激振动,例如加拿大的Lion Gate桥[1]、英国的Second Severn Crossing[2]等。涡激振动虽然不会造成桥梁在短期内垮塌,但可能导致结构的疲劳损伤,影响桥梁的正常使用,还有可能引起其他附属构件的破坏[3]。因此,有必要对涡激振动的相关特性开展研究,以明确涡激振动的发生条件、振动规律、影响因素和激发机理等。
风洞试验是桥梁抗风研究的主要方法之一,但由于风洞本身的限制,风洞试验可以实现的雷诺数与结构实际雷诺数存在较大差异,所以,试验结果与实际结果可能存在一定偏差。Schewe等[4]利用增压风洞实现了实桥级别的雷诺数,发现在低雷诺数下得到阻力系数高于高雷诺数下的结果,证实了雷诺数效应的存在。鲜荣等[5]对某扁平流线型悬索桥的不同尺度的节段模型进行了涡激振动试验,结果发现大比例尺模型的涡激振动振幅比小比例模型的振幅要小。而崔欣等[6]在扁平流线型桥梁的涡激振动试验中发现大比例尺模型的涡激振动振幅较大。董浩天等[7]对某悬索桥的不同尺度的节段模型以及全桥模型模型进行了风洞试验,发现增大模型尺度后涡激振动的锁定区间变窄并提前,涡激振动的振幅降低。胡传新等[8]对扁平流线型桥梁的两种比例尺节段模型进行了同步测振、测压风洞试验,发现高雷诺的涡振响应大于低雷诺数,且涡激振动的起振风速低于低雷诺数。
总之,国内外的学者对扁平流线型桥梁断面涡激振动的雷诺数效应进行了研究,但通常仅选用了两个雷诺数进行对比试验,且试验结果之间存在差异,为了进一步研究扁平流线型箱梁涡激振动的雷诺数效应,探究涡激振动发生机理,本文针对某一扁平流线型箱梁,研究了三种雷诺数下风攻角与涡激振动特性和风压分布的关系,探讨了不同雷诺数下的风压分布对于涡激振动的雷诺数效应的贡献。
1 风洞试验
风洞试验在石家庄铁道大学风工程研究中心STDU-1风洞的低速试验段进行,试验段宽4.4 m,高3 m,可实现风速范围1.5~30 m/s,紊流度≤0.4%。选取某一实际斜拉桥的扁平流线型箱梁作为研究对象,主梁宽32 m,高3.5 m,宽高比为9.14,风嘴角度为57°。考虑试验段、主梁尺寸和阻塞度的要求,确定模型缩尺比为1∶55,模型宽0.58 m,高0.064 m,长1.16 m。模型以钢管和加劲肋板为骨架,外覆ABS板材,保证模型具有足够的刚度。在模型的1/2截面处布置了1圈测压点,测压点数量为150,尖角部位流动更加复杂,该部位的测压点进行适当加密。模型及测压点布置示意图如图1所示。主梁模型通过两端的刚臂分别连接4根弹簧,弹簧则固定在风洞外的刚性框架上,模型两端还安装了0.82 m×0.19 m的矩形端板,以消除端部的影响[9],安装好的弹性模型系统如图2所示。
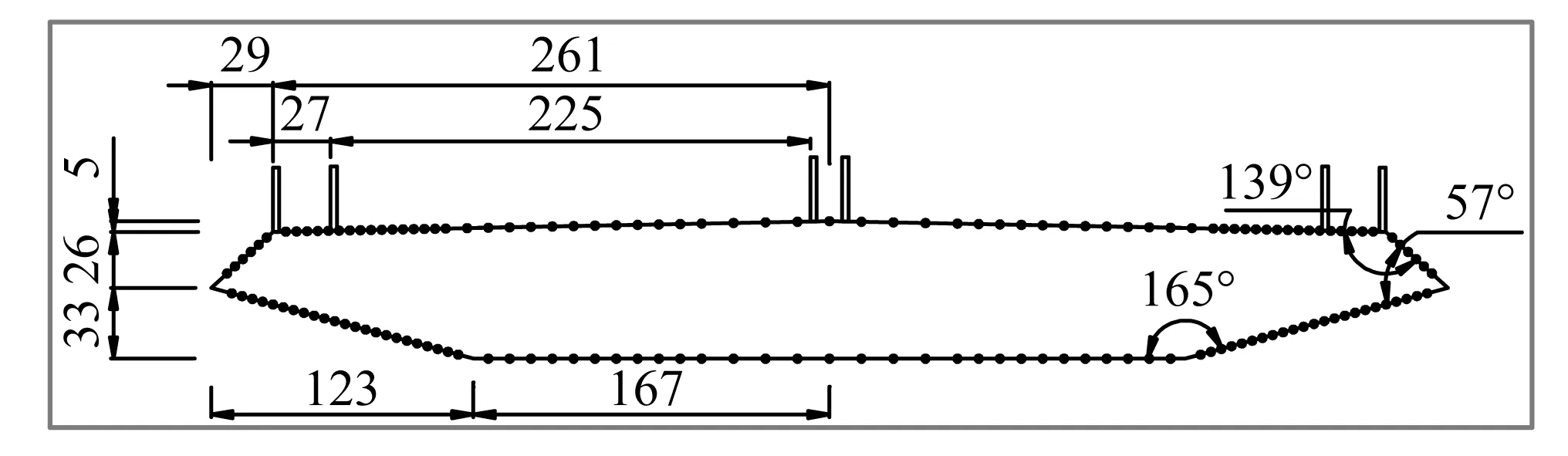
图1 模型及测压点布置示意图(mm)Fig.1 Model and pressure measuring point layout(mm)

图2 弹性模型系统Fig.2 Elastic model system
风攻角α定义为来流方向与模型上下表面分界线之间的夹角,当来流方向与分界线重合时,风攻角为α=0°。模型顺时针转动,风攻角增大,反之减小,试验风攻角为α=+5°,α=+3°,α=0°,α=-3°和α=-5°。
雷诺数表征的是流体的惯性力与黏性力之比,可以通过式(1)计算。
(1)
式中:U为来流风速;D为模型特征尺寸,此处取为模型高度;ρ为空气的密度;μ为空气的动力黏性系数;ν为空气的运动黏性系数。
为了研究涡激振动的雷诺数效应,通过更换模型两端的弹簧,得到三套具有不同自振频率的模型系统,依次进行试验,进而得到不同雷诺数下的涡激振动。三次试验分别记为试验(1)、试验(2)和试验(3),通过自激试验得到三套模型的自由衰减曲线,利用FFT变换得到频谱,如图3所示,进而计算出自振频率和阻尼比,三套模型的自振频率分别为3.4 Hz,5.5 Hz和8.2 Hz,阻尼分别为0.12%,0.11%和0.11%。

图3 模型自由衰减曲线及频谱Fig.3 Model free attenuation curve and spectrum
2 试验结果及讨论
为了便于分析模型表面的风压分布规律,现针对模型表面测压点,定义了一种无量纲距离。
Dd=d/D
(2)
式中:d为沿测压点所在表面从测压点到A点的距离;D为沿测压点所在表面从B点到A点的距离,部分测压点无量纲距离示意如图4所示。

图4 测压点无量纲距离示意图Fig.4 Dimensionless distance diagram of pressure measuring point
2.1 主梁涡激振动特性及雷诺数效应
三组试验在α=+5°和α=+3°均出现了明显的振动,而在其他风攻角下没有发现明显的振动。对α=+5°下的位移时程和频谱图进行分析,发现振动为单一频率的限幅振动,振动频率与自振频率一致,且振动仅发生在某一段风速区间内,据此判断观察到的振动为涡激振动,试验(1)α=+5°位移时程和相应的频谱图,如图5所示。
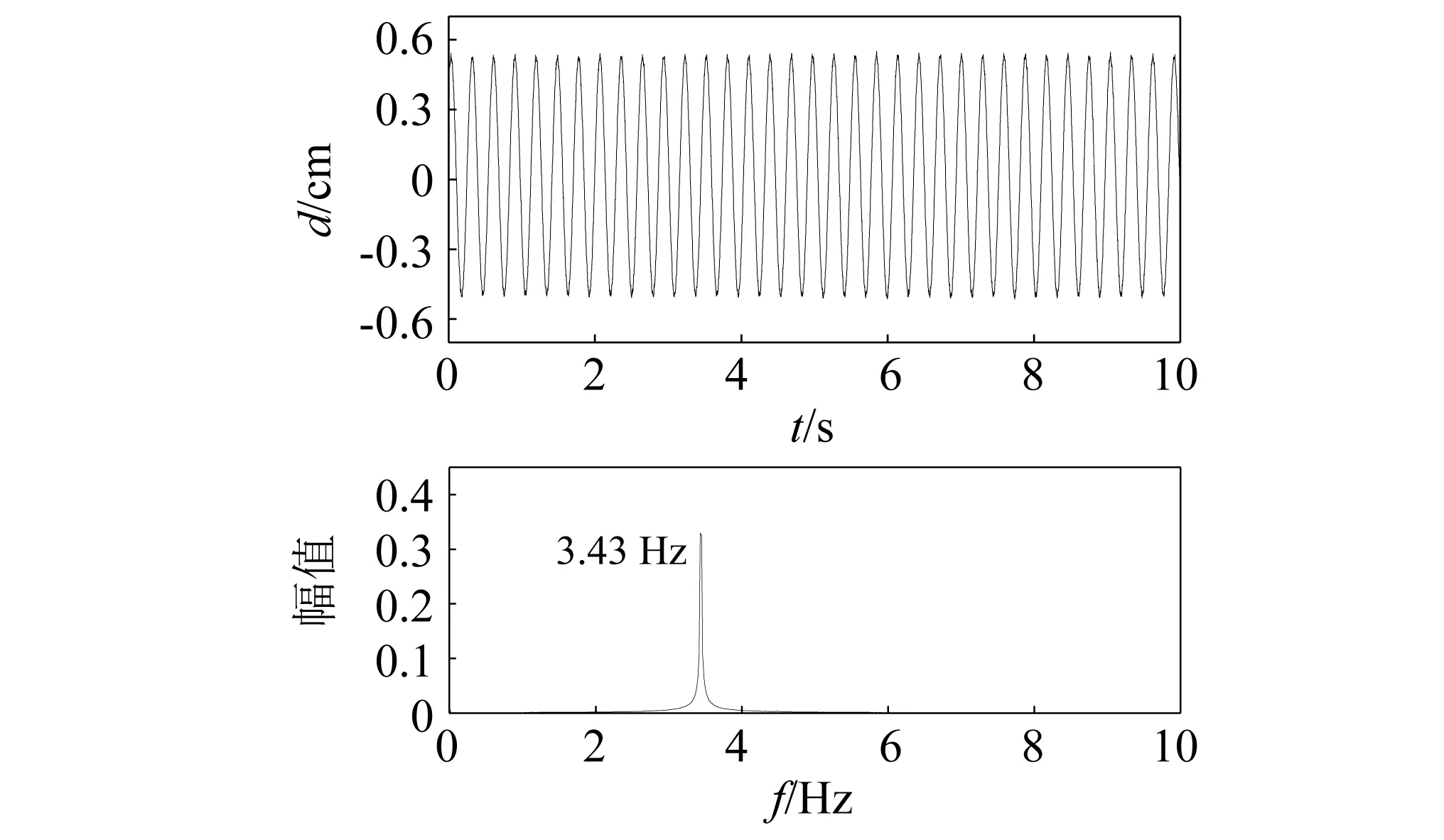
图5 试验(1)α=+5°位移时程曲线和频谱图Fig.5 Test (1)α=+5°displacement time-history curve and spectrum diagram
图6为三组试验分别在α=+5°和α=+3°时的振幅随风速的变化情况,表1列出了三组试验的具体振动结果。可以看出,风攻角对涡激振动存在显著影响,风攻角越大,涡激振动越剧烈,α=+5°时模型的最大振幅大于α=+3°时的量值,且发生涡激振动的风速相对更低。这表明涡激振动对气动外形十分敏感,当风攻角增大时,气动外形发生变化,旋涡脱落强度更大,从而在更低的风速下激发出更显著的涡激振动。另外,无论是α=+5°还是α=+3°,随着雷诺数的增大,模型的最大振幅都呈逐渐减小的规律,表明雷诺数效应会导致振幅估计偏差。这与崔欣等[6]和张伟等[10]针对不同断面形式的主梁雷诺数效应的研究结果基本一致。需要说明的是,由于通过调整模型系统的自振频率来改变涡激振动的发生雷诺数,阻塞度、长宽比等都保持不变,三组试验的唯一变量为雷诺数,因此,可以认为振幅的改变是雷诺数效应的结果。试验是在连续几天内完成,可认为三组试验的温度、湿度和压强等相关参数没有显著的改变。

图6 α=+5°和α=+3°三组试验振幅随风速变化曲线Fig.6 Amplitude changing with wind velocity at α=+5°, α=+3°
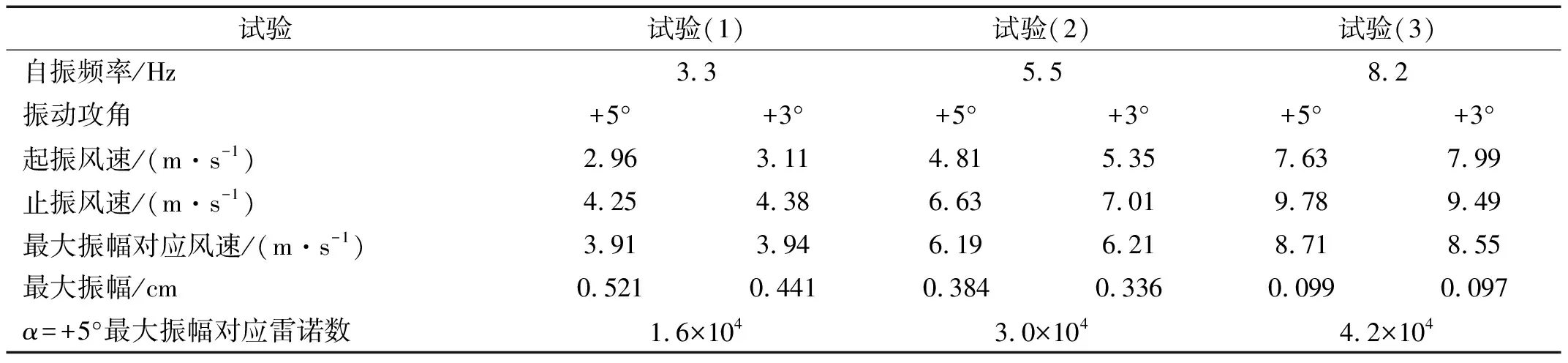
表1 三组试验模型涡激振动结果
图7为试验(1)在α=+5°和α=+3°下,不同风速的旋涡脱落频率。可以看出,非振动区间旋涡脱落频率-风速曲线为一直线,计算的斯特罗哈数St≈0.19,据此预测的涡激振动起振风速约为1.2 m/s,但在该风速并未观察到明显的涡激振动。而发生明显涡激振动的风速区间在3.2~4.4 m/s,且该锁定不同于以往观察到的直线型锁定,而是在进入涡激振动风速区间后涡脱频率突然下降至模型的自振频率,表现为凹陷型锁定。在国内外学者针对扁平流线型箱梁的涡激振动试验中,多锁定区间的涡激振动现象被多次发现[11-12]。
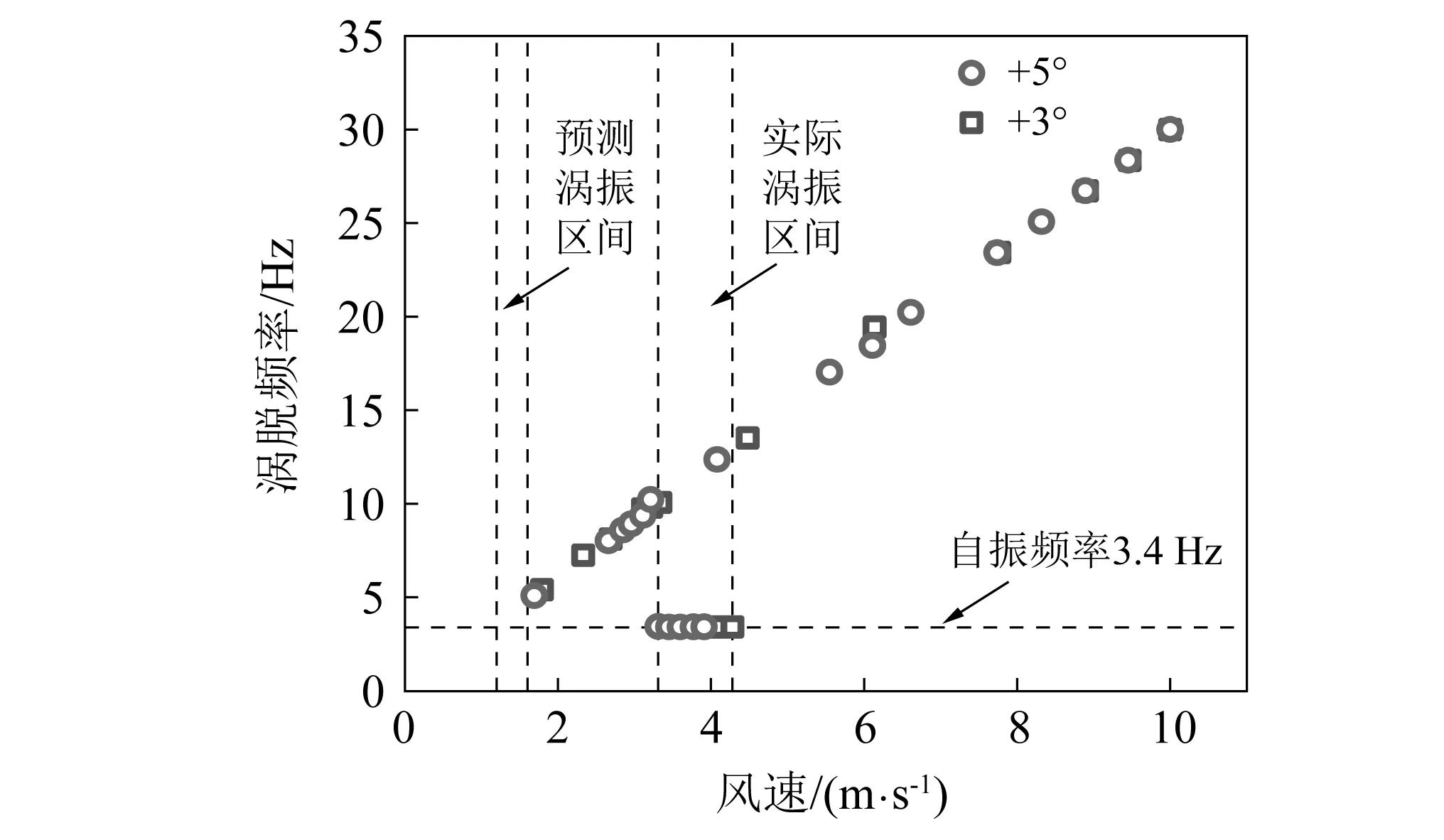
图7 试验(1)α=+5°和α=+3°涡脱频率随风速变化Fig.7 Variation in vortex shedding frequency with wind velocity at α=+5°, α=+3° for test (1)
根据文献[13],涡激振动出现多个锁定区间可能是由不同频率的旋涡脱落导致的,传统的St数仅反映强度最大或尺寸最大的旋涡脱落,而脱落的漩涡中存在不同尺度的旋涡,导致气动力也会含有丰富的频率成分,当某一主要频率与模型的自振频率接近时,就可能激发涡激振动。图8为试验(1)在振动区间内某个风速下的升力系数时程及其频谱图,可以看出,升力系数的卓越频率为3.4 Hz,正好与振动模型的自振频率一致,因此激发了明显的涡激振动。因此,判断涡激振动是否发生和发生的风速范围不能仅仅依赖St数来预测,宜通过风洞试验、数值模拟等方法并结合相关实测数据进行确定。
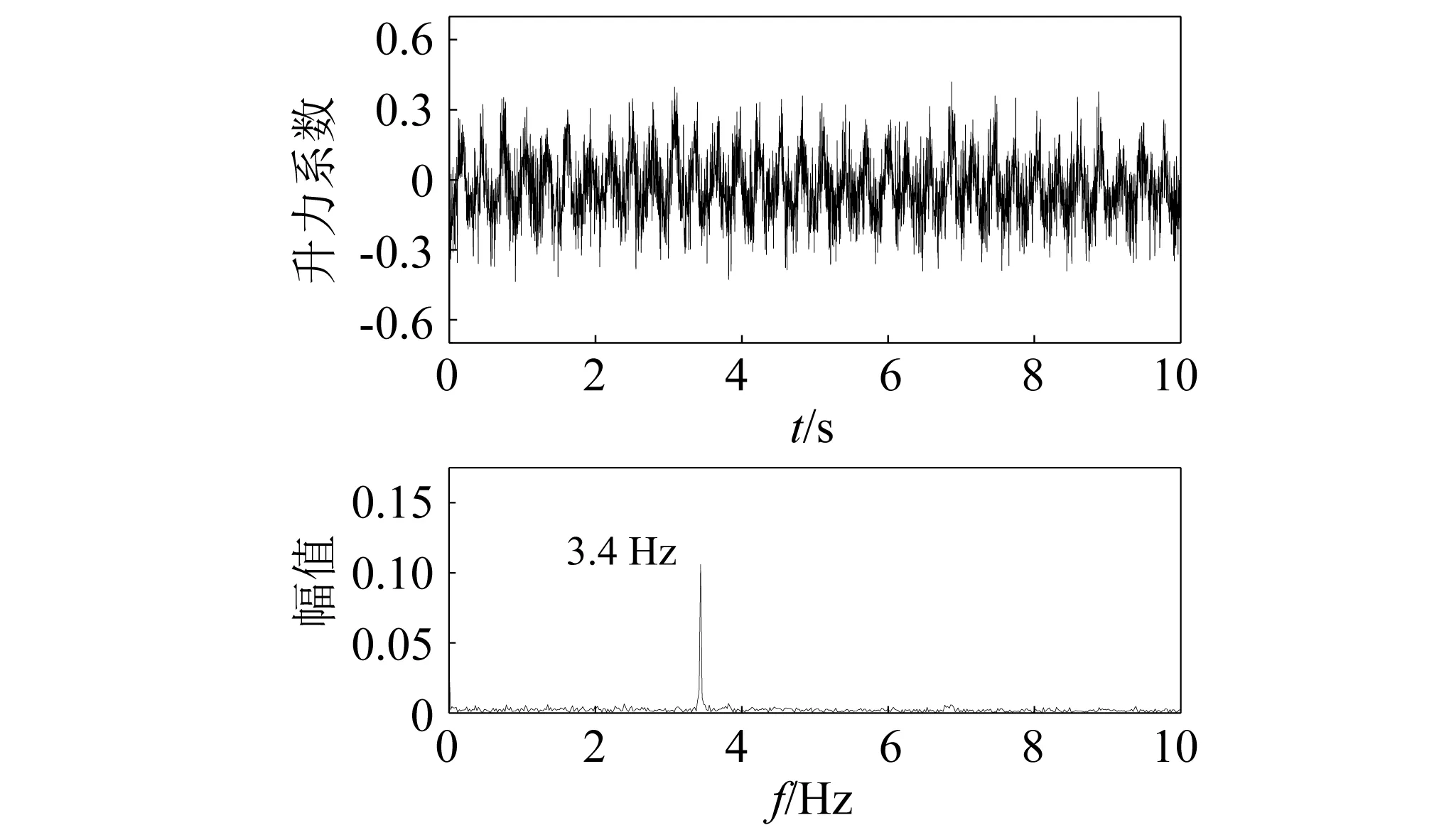
图8 试验(1) 振动区间内升力系数时程与频谱Fig.8 Test (1) time history and frequency spectrum of lift coefficient in vibration range
2.2 主梁表面风压分布规律
为了揭示涡激振动的深层机理,对模型表面的压力分布规律进行研究,表面压力可以通过风压系数来表征,风压系数定义如式(3)所示
(3)
式中:P为前方来流的静压;U为前方来流的速度;ρ为空气密度;p(i)为测得的模型表面压力信号的时间序列。测点的平均风压系数为测点风压系数时间序列的平均值,测点的脉动风压系数为测点风压系数时间序列的标准差。
根据表1可知,三组试验中在α=+5°时,最大振幅对应的雷诺数分别为Re=1.6×104,Re=3.0×104和Re=4.2×104,为了研究雷诺数对风压分布的影响规律,选择这三个雷诺数下的风压分布进行对比分析,平均风压分布如图9所示。

图9 不同雷诺数下平均风压分布Fig.9 Mean pressure distribution under various Reynolds numbers
首先,可以看出,主梁上下表面的平均风压分布差异明显,对于上表面而言,来流端风嘴附近处的平均风压系数绝对值最大,沿着上斜腹板,平均风压系数稍微减小,而在通过上斜腹板尖角时,平均风压系数突然变化为负值,之后沿着上表面往下游方向,平均风压系数没有明显变化,只在尾部栏杆扶手处出现较小波动。下表面的平均风压分布曲线为典型的双极值曲线,这是因为第一下斜腹板、腹板、第二下斜腹板的平均风压分布呈现不同规律,在第一下斜腹板和腹板,腹板和第二下斜腹板交点位置处出现两个极值点。在第一下斜腹板上,不同攻角下的规律也不同,后面会详细分析;在腹板上,平均风压系数的绝对值除了在两端极值点处有所提高外,其他位置基本保持不变;在第二下斜腹板,平均风压系数的绝对值沿着下游方向略微减小。
再者,对于上表面来说,风攻角仅改变平均风压系数的数值,但并未改变平均风压的整体分布规律。从α=-5°~+5°,随着风攻角的增大,上斜腹板承受的风压力逐渐减小,腹板承受的风吸力则越来越大。下表面的腹板和第二下斜腹板均主要承受风吸力,在负攻角时承受的吸力略大,受风攻角的影响相对较小。第一下斜腹板的平均风压受风攻角的影响非常显著,随着无量纲距离的增大,平均风压系数的绝对值先逐渐减小后逐渐增大,在α=+5°和α=+3°时,平均风系数最开始为正值,后逐渐变为负值;对于其他风攻角而言,平均风压系数主要为负值,仅在α=0°时,风压系数增大的过程中,存在几个正值,表明气流在尖嘴处就发生了分离,且风攻角越小,分离越明显。
最后,对比不同雷诺数下的平均风压分布规律,发现雷诺数的提高没有对主梁上下表面在各风攻角下的平均风压整体分布规律产生显著影响,仅仅是数值发生了细微的改变,其中,雷诺数的改变对于下表面的平均风压系数数值影响较上表面较大。
脉动风压分布如图10所示,主梁上下表面的脉动风压分布也存在显著不同,对于上表面,在不同的风攻角下,脉动风压分布呈现不同规律,在α=+5°和α=+3°时,前缘和尾部的脉动风压系数较大,α=+5°的脉动风压系数较α=+3°时更大,而在其他风攻角下,脉动风压系数较小且分布较为均匀。随着雷诺数的增大,脉动风压系数减小,在Re=4.2×104时,所有风攻角下的脉动风压系数均非常小。
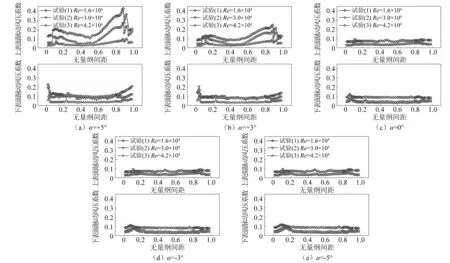
图10 不同雷诺数下脉动风压分布Fig.10 Fluctuant pressure distribution under various Reynolds numbers
对于下表面来说,除了α=+5°和α=+3°在Re=1.6×104下的前缘端和尾部端存在较大的脉动风压系数,其余的风攻角和雷诺数工况下,脉动风压系数均非常小。脉动风压系数是由旋涡脱落引发的,其大小可以反映旋涡脱落的强度,进而解释涡激振动。根据主梁上下表面的脉动风压分布规律,可以认为上表面是决定涡激振动是否发生以及涡振响应强度的关键。并且,脉动风压系数随着雷诺数的增大而减小是导致涡激振幅减小的深层次原因。
2.3 测点气动力相关性和涡激振动贡献系数
模型部分测点存在较大的脉动风压系数,可能对涡激振动的产生造成了影响。为了进一步探究模型表面不同区域对涡激振动的影响,针对三次试验的气动力相关性系数和涡激振动贡献系数进行了分析。
模型表面测点的风压与该测点代表面积的乘积可以表示测点代表区域所受到的气动力,而整个箱梁断面的气动力可通过对所有测点的气动力积分得到,两者间的相关性用相关系数ρ来衡量,定义如式(4)所示
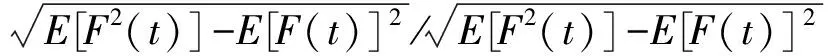
(4)
式中:f(t)为模型表面某一个测点所代表的面积受到的升力;F(t)为整个箱梁断面受到的升力。仍然考察Re=1.6×104,Re=3.0×104和Re=4.2×104的相关情况,研究雷诺数对相关系数的影响规律。图11为不同雷诺数下α=+5°的相关系数曲线。

图11 不同雷诺数下α=+5°模型气动力相关性系数Fig.11 Aerodynamic correlation coefficient of α=+5° model at different reynolds numbers
可以看出,在Re=1.6×104时,上表面只有在Dd≥0.942的很小范围内,相关系数在0附近,其余测点的相关系数均在0.4附近,且波动较小。在Re=3.0×104时,上表面Dd=0.500附近测点的相关系数下降至0值附近,其余部分与Re=1.6×104的相关系数相当。当雷诺数增大到Re=4.2×104时,前半部分的相关系数也明显减小。下表面的相关系数基本呈现单峰式曲线,随着雷诺数的增大,整体曲线呈现出上升趋势Re=1.6×104时的相关系数最大值约为Re=4.2×104最大值的47%。可以看出,雷诺数会显著影响主梁上下表面的相关系数,但是影响规律却不同。随着雷诺数的增大,上表面的相关系数逐渐减小,而下表面的相关系数逐渐增大。这表明由于雷诺数效应导致的主梁平均升力的变化,上、下表面对主梁的贡献是相反的。
为了研究主梁表面测点对涡激振动的贡献情况,特引入涡激振动贡献系数CR,定义为测点脉动风压系数和该测点相关系数的乘积,如式(5)所示
CR=Cp,rms·ρ[F(t),f(t)]
(5)
式中,Cp,rms为测点的脉动风压系数。不同雷诺数下α=+5°的测点涡激振动贡献系数曲线,如图12所示。
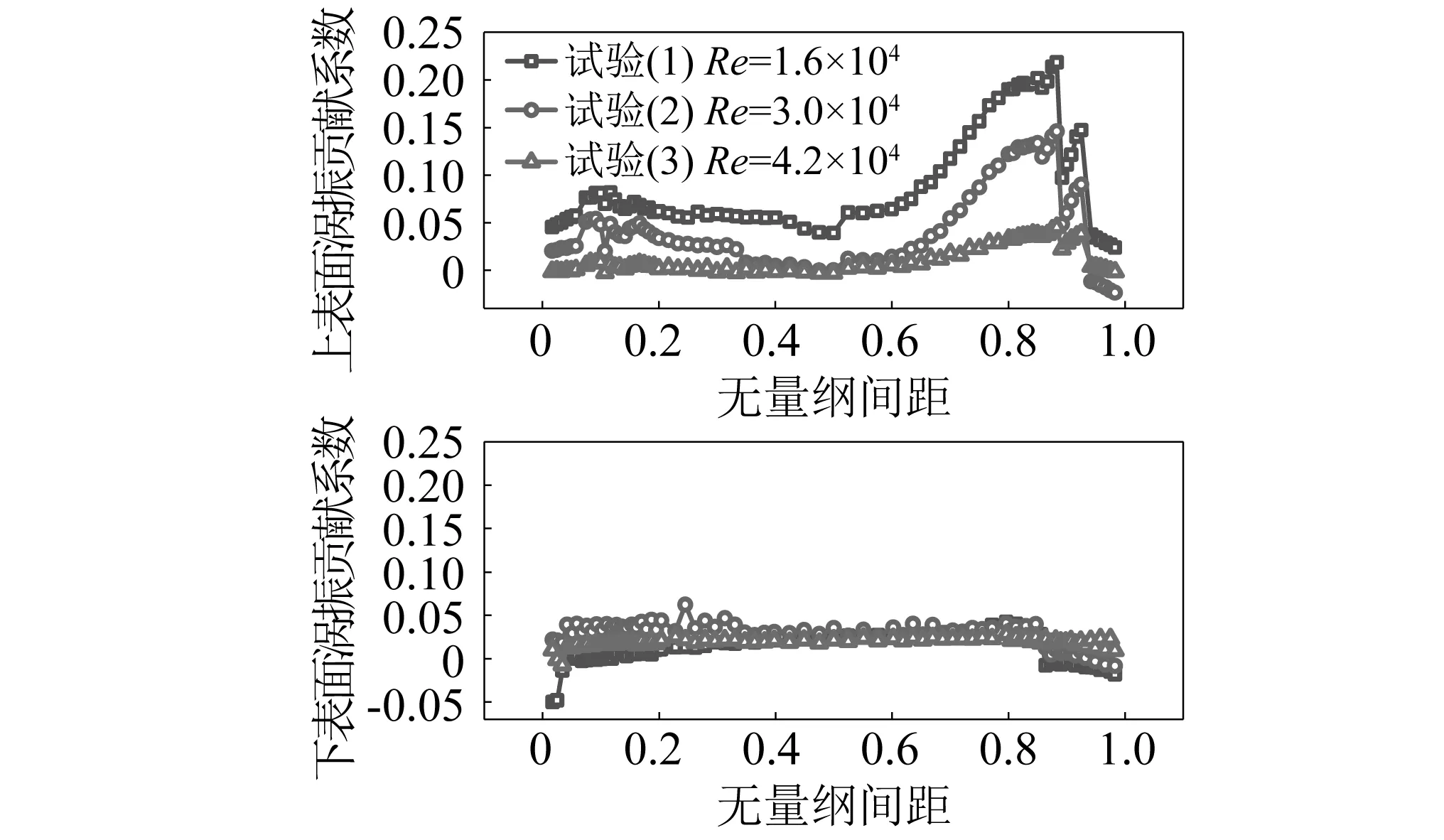
图12 不同雷诺数下α=+5°模型涡激振动贡献系数Fig.12 Contribution coefficient for vortex-induced vibration for α=+5° at various Reynolds numbers
根据图12可得,在不同雷诺数下,涡激振动贡献系数沿上表面的分布整体规律是接近的,即在无量纲间距Dd≤0.5时,涡激振动贡献系数较小,但整体分布较均匀;当0.5≤Dd≤0.883时,随着无量纲间距的增大,涡激振动贡献系数逐渐增大;当0.883≤Dd时,涡激振动贡献系数又开始减小。但是在不同的雷诺数下,在相同的无量纲位置,涡激振动贡献系数的数值不同,且雷诺数越大,涡激振动贡献系数越小,这和涡激振动振幅随雷诺数增大而减小的规律是一致的。
下表面的涡激振动贡献系数较小,数值在0附近,涡激振动贡献系数沿下表面分布非常均匀,且随雷诺数变化很小,表明下表面对涡激振动及涡激振动的雷诺数效应的贡献均较小。
可以得出,针对研究涉及到的扁平流线型箱梁断面,箱梁上表面下游区域对涡激振动的贡献较大。脉动风压系数和气动力相关系数随雷诺数的变化可能是导致涡激振动雷诺数效应的原因之一,其中,脉动风压系数的变化造成的影响相对较大。
3 结 论
通过风洞同步测振和测压试验,对扁平流线型箱梁的涡激振动特性及雷诺数效应进行了研究,主要得出以下结论。
(1)扁平流线型箱梁的竖弯涡激振动存在明显的雷诺数效应,低雷诺数下的涡激振动振幅要大于高雷诺数下的振幅,用低雷诺数下的结果来预测实桥的振幅偏于安全。
(2)由于旋涡脱落的复杂性,涡激振动可能出现在根据斯特罗哈数预测的风速区间之外,涡激振动测试建议通过风洞试验、数值模拟等方法结合实测数据确定。
(3)箱梁上表面下游方向的半个区域对涡激振动的贡献较大。模型的脉动风压系数随雷诺数的改变,可能是造成涡激振动雷诺数效应的原因。

