Z型梁结构压电式能量采集性能分析

施海天， 魏 莎,2， 丁 虎,2， 陈立群,2

(1.上海大学 力学与工程科学学院， 上海 200444；2.上海市应用数学和力学研究所， 上海 200072)

近年来，随着石油、煤炭等资源的日益减少，人类对能源的需求不断增加，能源问题已成为人类亟待解决的重要问题。从外部环境振动中获取能量是目前国内外研究热点之一，振动型能量采集器将环境中普遍存在的机械能转换为电能，可以实现自供能传感、控制与驱动，具有灵活、节能环保、可持续等优势，在航空航天、生物医疗、工业生产、交通监管、环境监测和军事侦查等领域均具有广阔的应用前景[1-5]。压电式能量采集器因其功率密度高、设计灵活等特点，已成为重要的振动能量采集方式之一。

压电悬臂梁式振动型能量采集器在外激励频率接近固有频率时可实现有效的能量采集效果，但在远离共振区域时，其采集性能将大幅降低。由于一般工程环境中的振动常具有较宽的频带，所以设计的能量采集器需拓宽频带，提高能量采集性能。目前拓宽频带的方式主要有多结构阵列、多模态转化、非线性设计等方法[6-10]。在结构阵列设计方面，Song等[11]设计了一种磁耦合压电式能量采集器阵列，实现双重能量采集模式，对杂散磁场和环境振动均可实现有效能量采集。Xie等[12]设计了一种L型压电耦合圆筒式能量采集器，通过阵列式L型结构，有效地提高了能量采集的频带带宽。在多模态转化方面，Liu等[13]利用聚偏氟乙烯压电薄膜制备了一种由两个不同结构尺寸悬臂梁组成的双谐振能量采集器，该能量采集器可以将工作频带由37～51 Hz拓宽至30～52 Hz并输出0.12～0.19 μW的功率。马天兵等[14]设计了一种多层折叠梁结构，在较低的频率范围内实现多个模态的能量采集，有效地提高了压电能量采集的性能。在非线性设计方面，邹鸿翔等[15]利用屈曲梁结构设计了二维平面内采集振动能量的装置，通过合理设计，面内压电振动能量采集器可以在低频、宽频、弱激励下有效俘获能量。Jiang等[16]设计了一种带有振荡器的轴向加载压电式悬臂梁能量采集器，利用内共振机制，压电梁表现出硬化型非线性特征，使幅频峰值向两侧弯曲，能量采集的带宽得到较大的提高。Yang等[17]提出了一种将双稳态与内共振相结合的混合非线性压电能量采集器，与同结构的固定磁铁式双稳定系统相比，频率带宽增加了二倍。

尽管在压电悬臂梁式振动型能量采集器的基础上，一些学者为拓宽能量采集带宽进行了不同方式的梁结构优化与改进，但结合实际工程应用，仍然较难实现宽频带、多频率和多维度能量采集性能。本文设计了Z型梁结构压电式能量采集器，理论分析了Z型梁的固有特性，并采用有限元方法验证其准确性。通过研究发现，Z型梁结构压电式能量采集器在满足一定外激励的情况下，可发生不同模态间的相互作用，实现不同模态共振频率下的能量采集，并且通过优化结构参数后，可实现能量采集器工作频带的变化与拓宽，改善能量采集效果。

1 Z型梁结构能量采集器模型

1.1 结构设计

优化压电悬臂梁式结构能够有效的提高能量采集的性能，目前主要的研究有附加集中质量改变固有频率以匹配实际环境振动频率，非线性磁力的附加拓展频带，研究异型梁实现二自由度的能量采集等[18]，但仍然难以匹配实际工程中的激励宽频带、多方向等问题。结合实际梁的多模态、多自由度的特点，本文设计了一种Z型梁结构压电式振动能量收集器。图1为Z型梁结构三维模型示意图，Z型梁由3段矩型梁构成，以底层矩型梁作为压电材料基板，根据每段梁始末位置的边界条件，相互耦合得到总体模态，以此实现在一定范围内集中更多固有频率的目的。

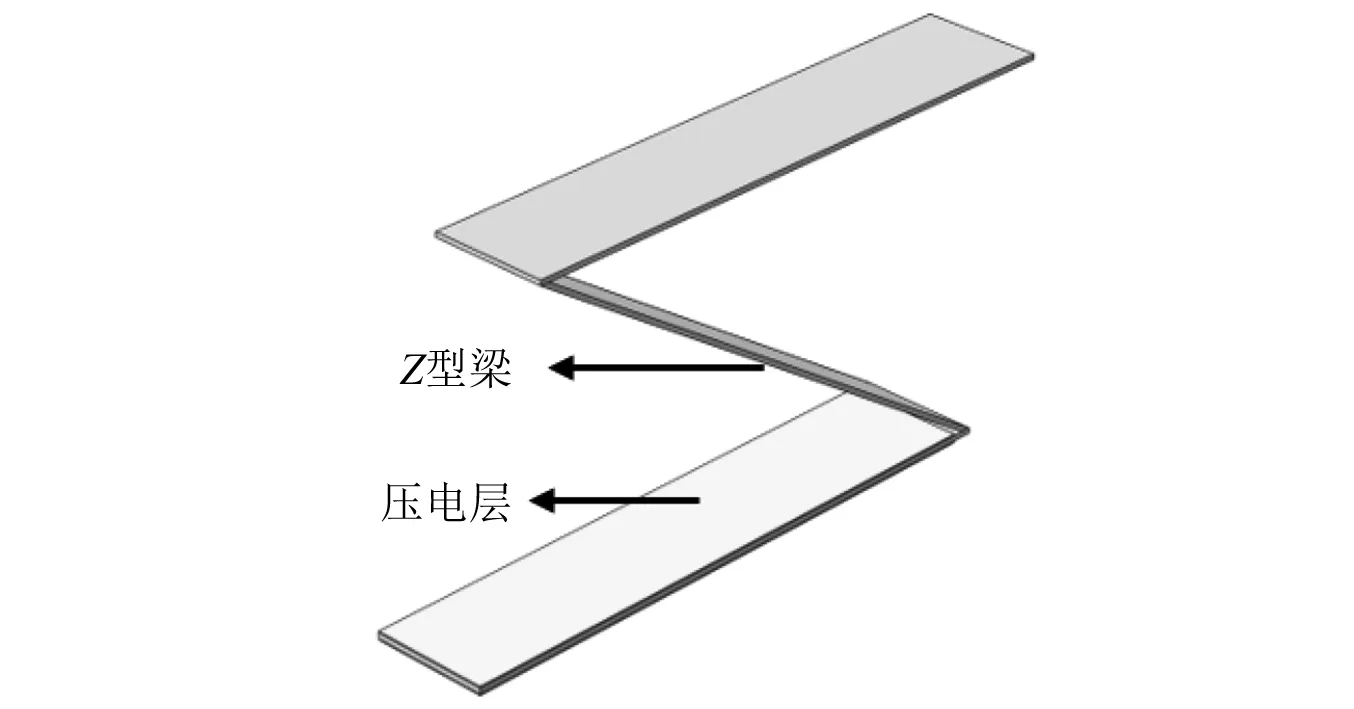
图1 Z型梁结构三维模型示意图Fig.1 Three dimensional model of Z-shapedbeam

1.2 动力学模型

图2(a)为Z型梁结构振型示意图，以各个角节点为原点建立单独坐标系，将Z型梁分段为三段单独的梁结构，由于梁的横向振动与纵向振动，产生了横向位移与纵向位移如图2(b)所示，在不考虑阻尼的情况下，每段梁的横向自由振动的运动方程为

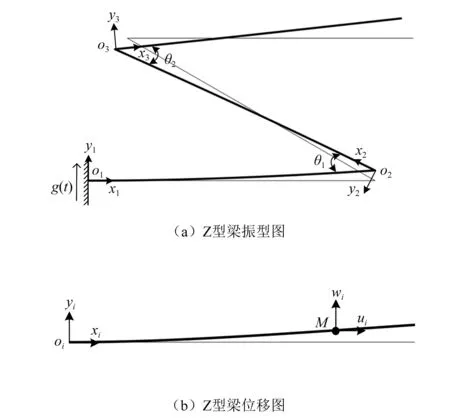
图2 Z型梁振型与位移示意图Fig.2 Vibration mode and displacement diagram of Z-shaped beam

(1)

每段梁的纵向自由振动的运动方程为

(2)

式中:Ei为第i段梁的弹性模量；Ii为第i段梁截面惯性矩;ρi为第i段梁密度;Ai为第i段梁的截面面积。

将控制方程中梁的横向与纵向自由振动进行如下分离变量

wi(xi,t)=Wi(xi)Q(t)

(3)

ui(xi,t)=Ui(xi)Q(t)

(4)

将式(3)、式(4)代入式(1)、式(2)，可得到模态函数与模态坐标的通解为

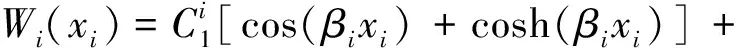
(5)

(6)

(7)

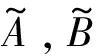
(8)

(9)

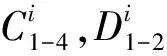
T·C=0

(10)

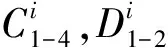
1.3 模态分析

为研究Z型梁的结构参数对固有频率的影响，取梁的材质为铝，设计每段矩形梁的长宽厚尺寸为60 mm×12 mm×0.45 mm，材料的弹性模量为Ei=70 GPa，密度为ρi=2 700 kg/m3,泊松比为0.33，并取角度θ1=θ2，理论计算出角度变化对Z型梁的模态与固有频率的影响，并与有限元软件Comsol的仿真结果进行对比。

图3为不同角度下Z型梁固有频率的理论计算结果与有限元仿真结果。从图3中结果可以看到，两者较为吻合。当角度在0°～90°时，随角度增大，一阶固有频率减小，二阶固有频率增大，三阶固有频率略微降低；当角度大于90°时，一、二阶固有频率几乎不再变化，三阶固有频率增幅较大。由于Z型梁角度的变化会引起固有频率的较大变化，通过合理优化角度参数，可以提高Z型梁的模态集中性，设计合适的多模态、宽频带压电式能量采集器。

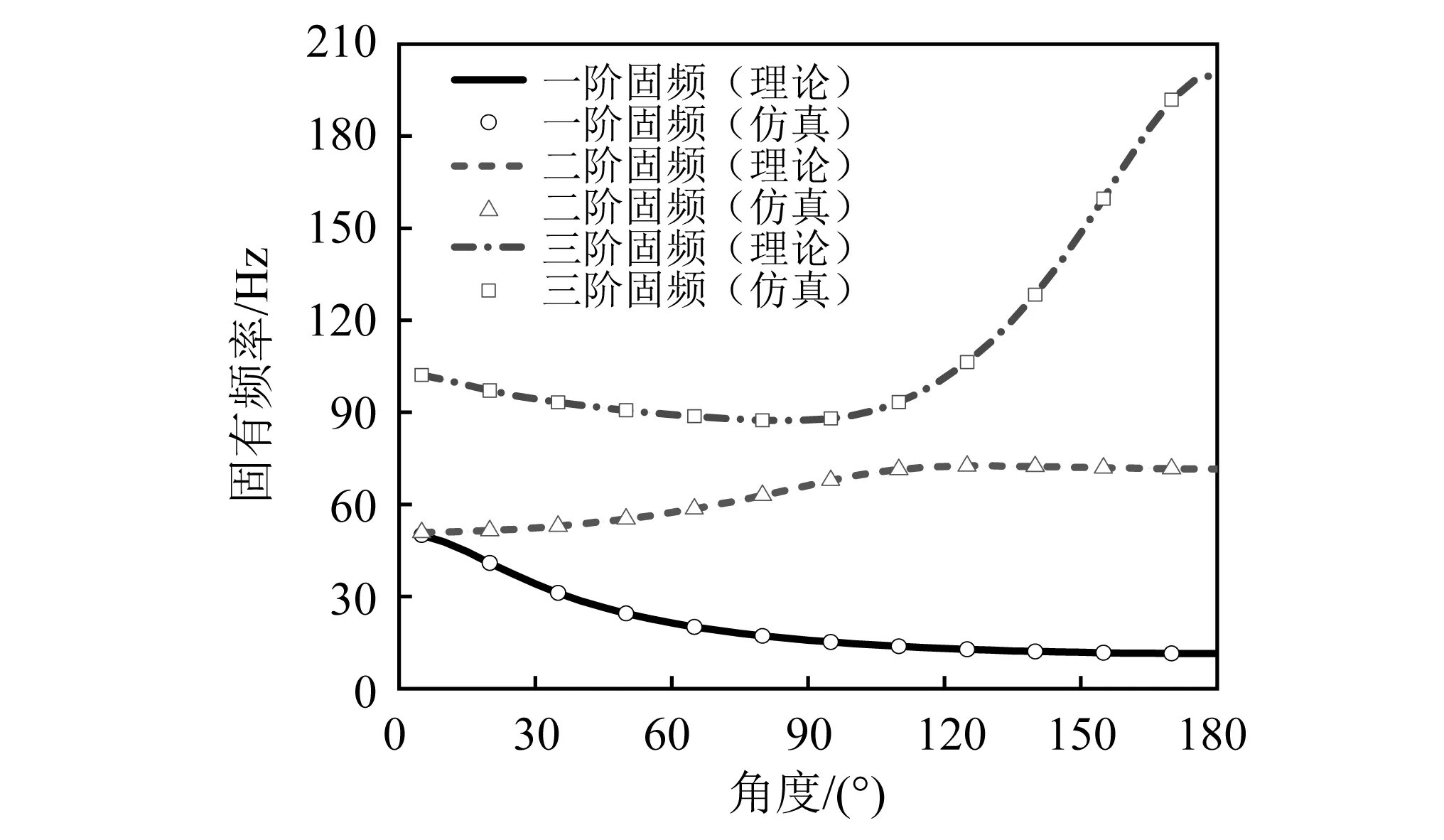
图3 不同角度下Z型梁结构的固有频率Fig.3 Natural frequency of Z-shaped beam under different angles

2 Z型梁结构有限元建模

Z型梁结构的机电耦合模型示意图,如图4所示。图4中能量采集器由Z型梁和双晶压电片构成，双晶PZT粘贴于Z型梁的第一段主梁上，并以并联方式连接于外接电路。

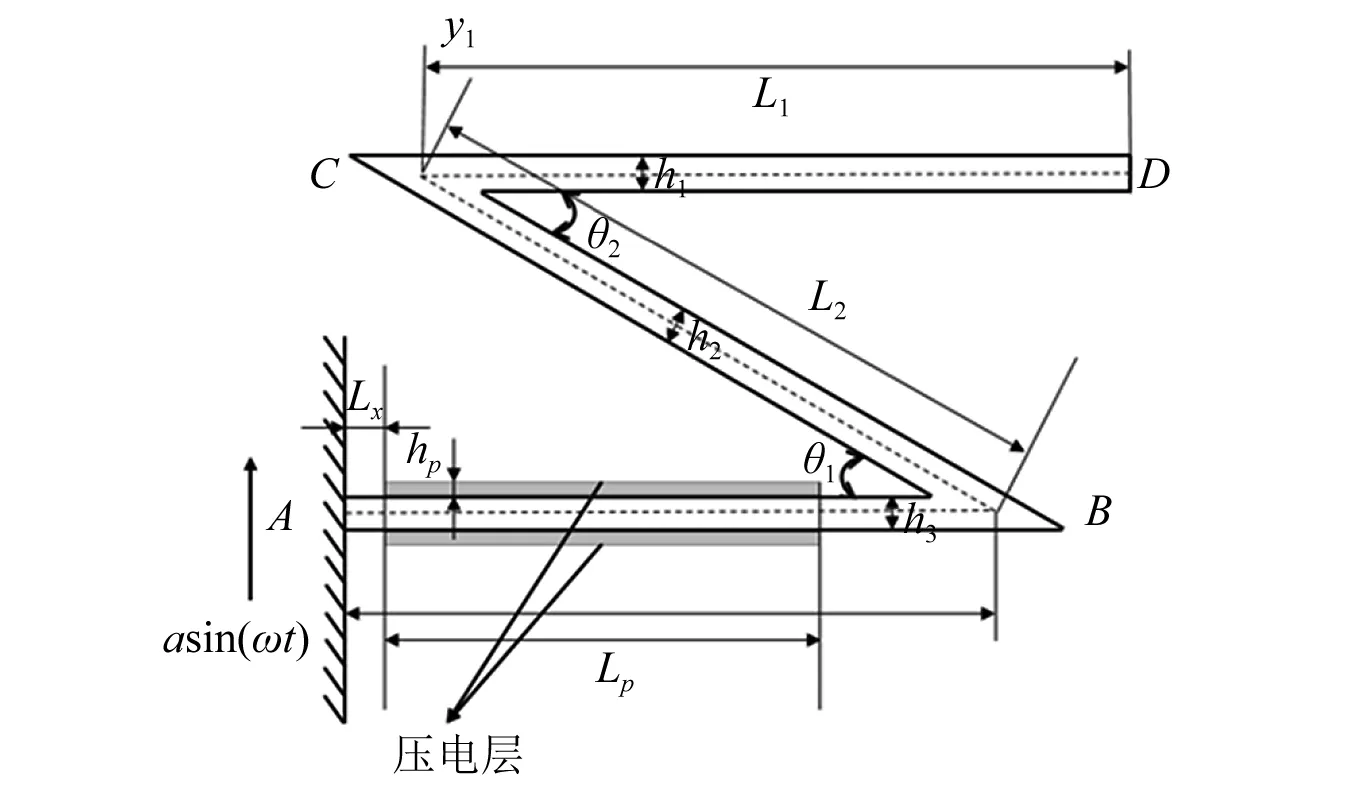
图4 型梁结构机电耦合模型示意图Fig.4 Schematic diagram of electromechanical coupling model of Z-shaped beam

建立Z型梁结构中压电材料的有限元数学模型，将压电材料和梁离散成若干个三角形单元,如图5所示。根据三角形单元内节点的关系，压电晶体的位移函数[20]为

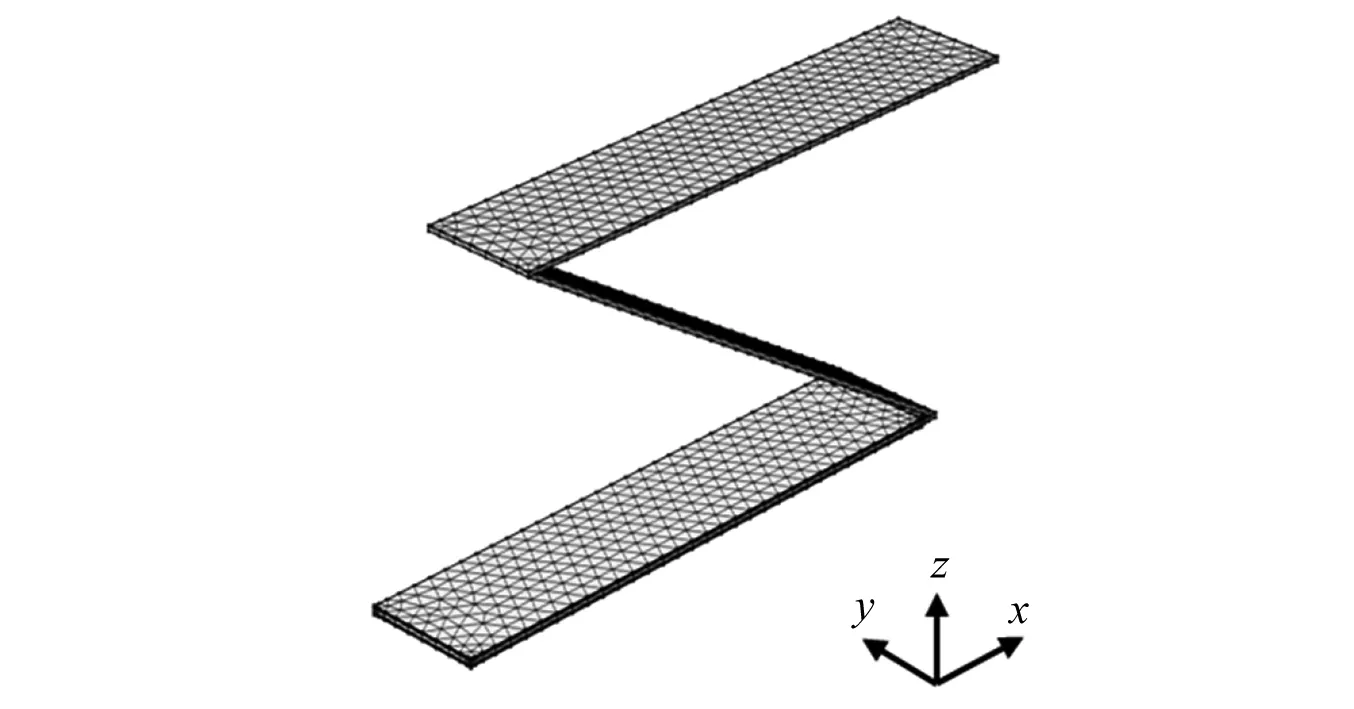
图5 Z型梁结构三角形网格划分示意图Fig.5 Finite element mesh generation of Z-shaped beam

(11)

式中:uc，Vc分别为三角形单元中任一点的矢量位移和电压矢量；u,V分别为节点位移矢量和节点电压矢量；Nu,Nν分别为位移形状函数和电压形状函数矩阵。

(12)

(13)

式中,Nn为第n个节点的形状函数，利用局部坐标可以将形函数表示为

Nn=(1+xxn)(1+yyn)(1+zzn)

(14)

通过节点的位移场和应变场可以求解节点电压强度和电位移密度。由此可以建立任何一个三角形单元的机电耦合电压动力学方程。

(15)

根据动力学方程式(15)，利用有限元软件Comsol可以分析得到简谐外激励力作用下Z型梁结构的任意一个压电单元的振动位移和输出电压V，将单元电压V利用软件耦合后可以得到Z梁结构的输出电压V0。

3 Z型梁结构参数分析与优化

为进一步深入研究Z型梁结构的振动能量采集性能，利用有限元软件Comsol构建Z型梁结构的三维模型，采用三角形单元划分网格，分析不同结构尺寸、激励大小方向以及外接负载等参数对Z型梁结构能量采集性能的影响规律。其基本参数如表1所示[21]。

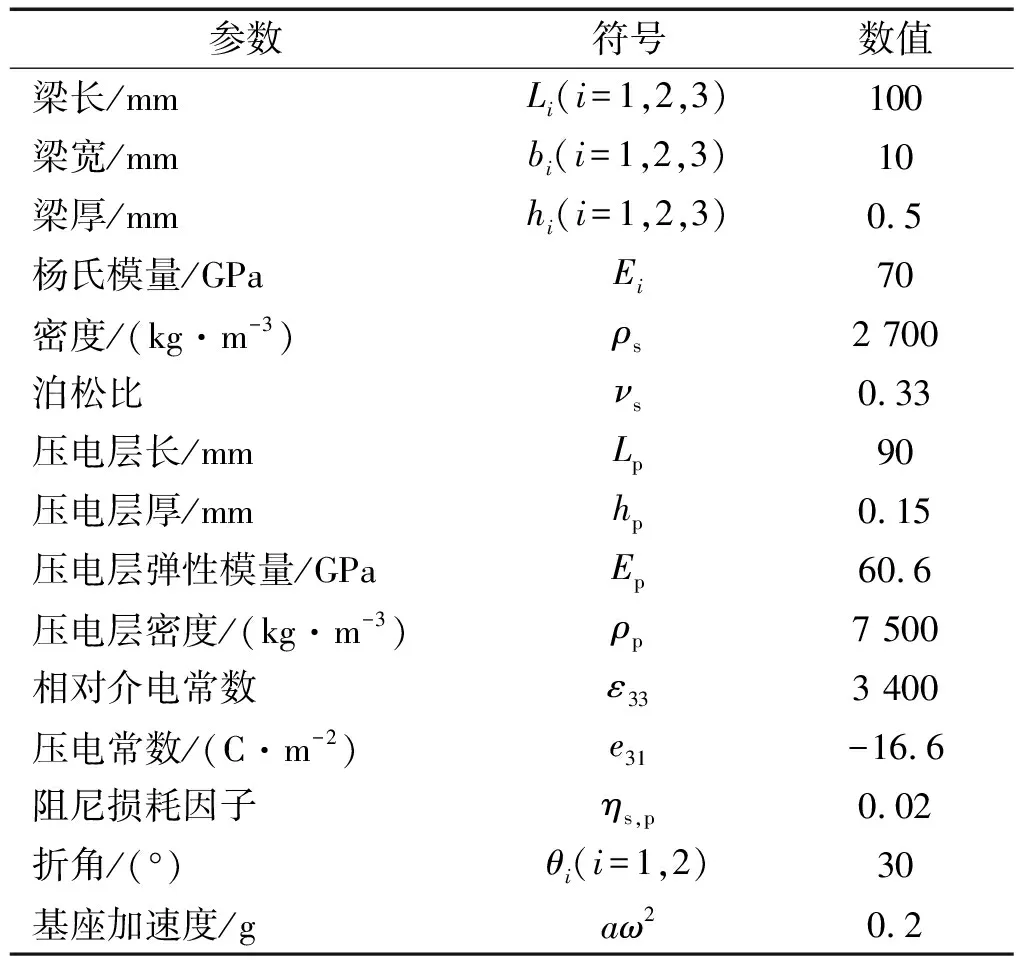
表1 Z型梁结构基本参数

与压电悬臂梁进行对比，取Z型梁结构第一段作为压电悬臂梁构型，并保持基本结构尺寸一致。为不失一般性，Z型梁结构的角度取为90°，在基座激励0.2g的加速度作用下，压电式悬臂梁与90°折角Z型梁结构的电压-频率曲线,如图6所示。由图6中可以看出，Z型梁结构相较于悬臂梁，在0～60 Hz内，电压响应幅值得到较大提高，同时模态频率也明显降低，出现第二个较高的电压峰值，可实现多模态能量采集。

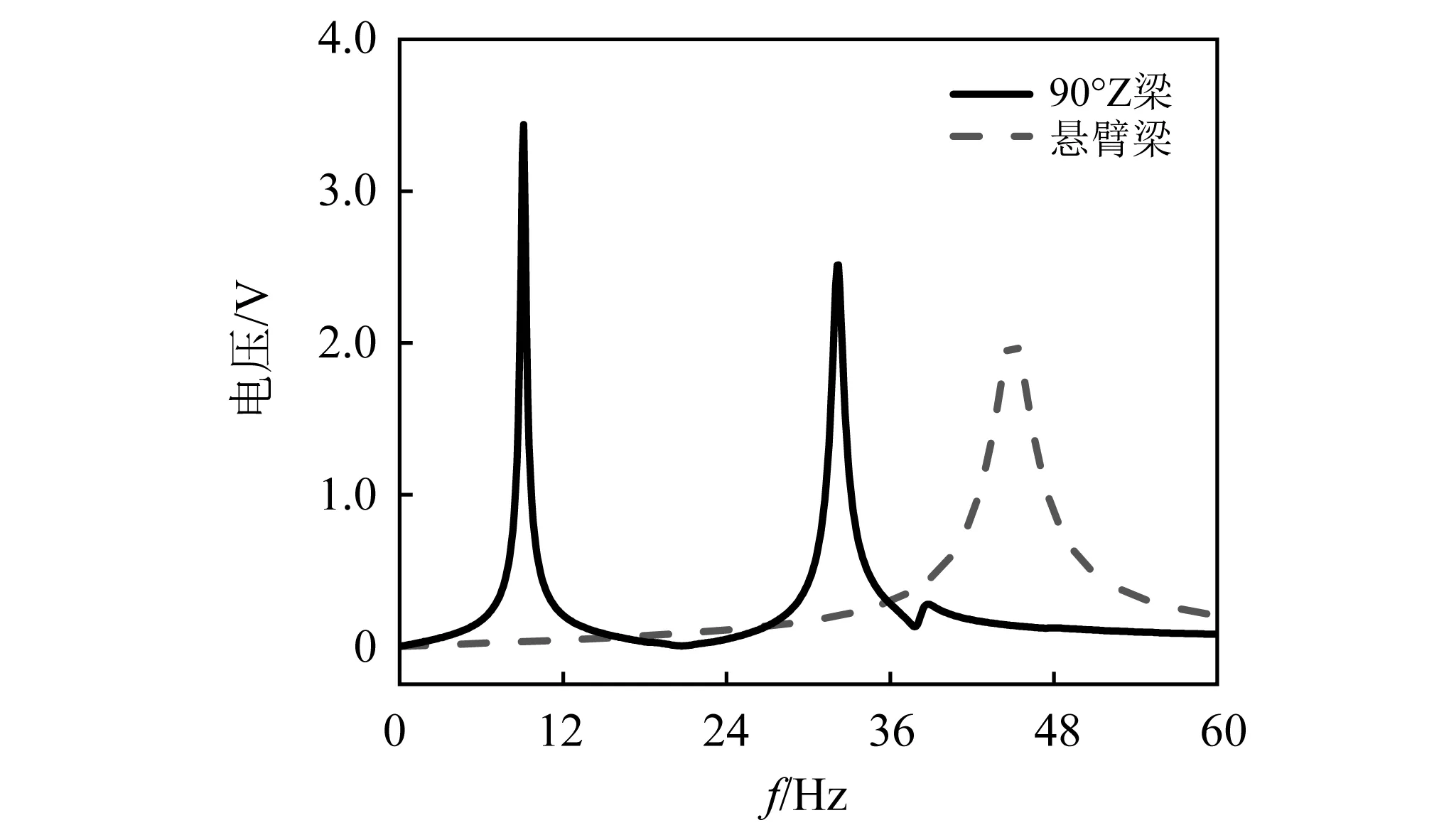
图6 压电悬臂梁与90°Z型梁结构电压-频率曲线Fig.6 Voltage frequency curve of piezoelectric cantilever beam and 90 ° Z-shaped beam structure

根据此前理论推导的Z梁固有频率和折角θi的关系可知，在折角大于90°后，除第三阶固有频率发生较大变化，第一、第二阶固有频率变化较小，因此不予研究。图7(a)为设计折角为0°～90°的Z型梁结构输出电压-频率曲线图。模态频率的变化规律与Z型梁的理论模态频率分析相符合，同时电压峰值也随设计折角发生变化。随着角度的增大，第一、第二阶固有频率的间距增大，电压峰值也随之增大，但相应的第三阶频率有所降低，电压峰值不断下降。在折角为90°时，第三阶模态的电压峰值非常低，难以实现能量的有效采集。图7(b)所示的功率随角度的变化规律与电压随角度的变化趋势一致，图7(c)所示的位移随角度的变化规律与电压随角度的变化趋势也一致。由图7中结果可知，通过角度的结构优化设计，可以有效的实现多模态能量采集，并且避免结构因大位移而产生破坏。

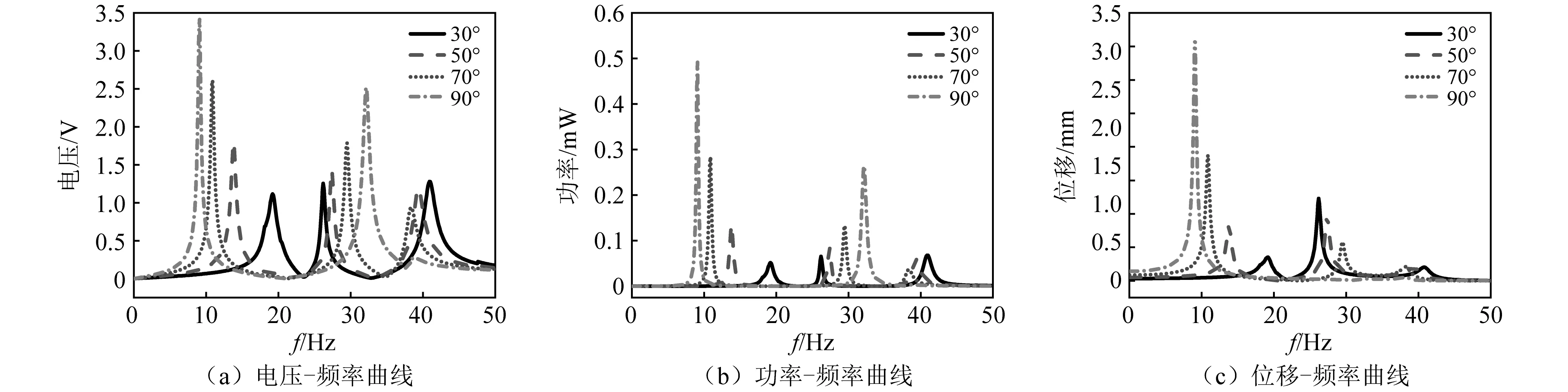
图7 不同角度下Z型梁结构电压-频率曲线、功率-频率曲线与自由端位移-频率曲线Fig.7 Voltage and free end displacement frequency curves of Z-shaped beam structure under different angles

为实现Z型梁结构的多模态能量采集，得到更加平稳的电压响应，设计Z型梁的结构夹角为30°，并保持表1中梁的基本参数不变，分析尺寸参数对压电能量采集性能的影响规律。保持带有压电层的主梁不变，改变第二、第三段梁的长度，不同段梁长的Z型梁结构电压-频率曲线，分别如图8和图9所示，梁长在一定范围变化时均可实现多个模态的有效电压能量采集。随第二段梁长的增大，一阶电压响应峰值先减后增，二阶和三阶电压响应峰值均增大。当第二段梁为120 mm和150 mm时，二阶电压响应的峰值和频率几乎不再变化。位移随梁长度的变化规律与电压随梁长度的变化趋势基本一致。如图9所示，随第三段梁长的增大，各阶固有频率均降低，自由端的位移均增大，一、二阶电压响应峰值先减后增，三阶电压响应峰值不断增大。图10为在三段梁长度同时变化下的Z型梁结构电压-频率曲线图。在长度为150 mm时，第一、第二阶固有频率非常接近，且出现细长的电压-频率曲线，但非共振带处电压值依旧非常低，并没有拓宽能量采集的工作频带。由此说明，在三段梁长度同时变化的情况下，不能显示出更宽频的能量采集性能。

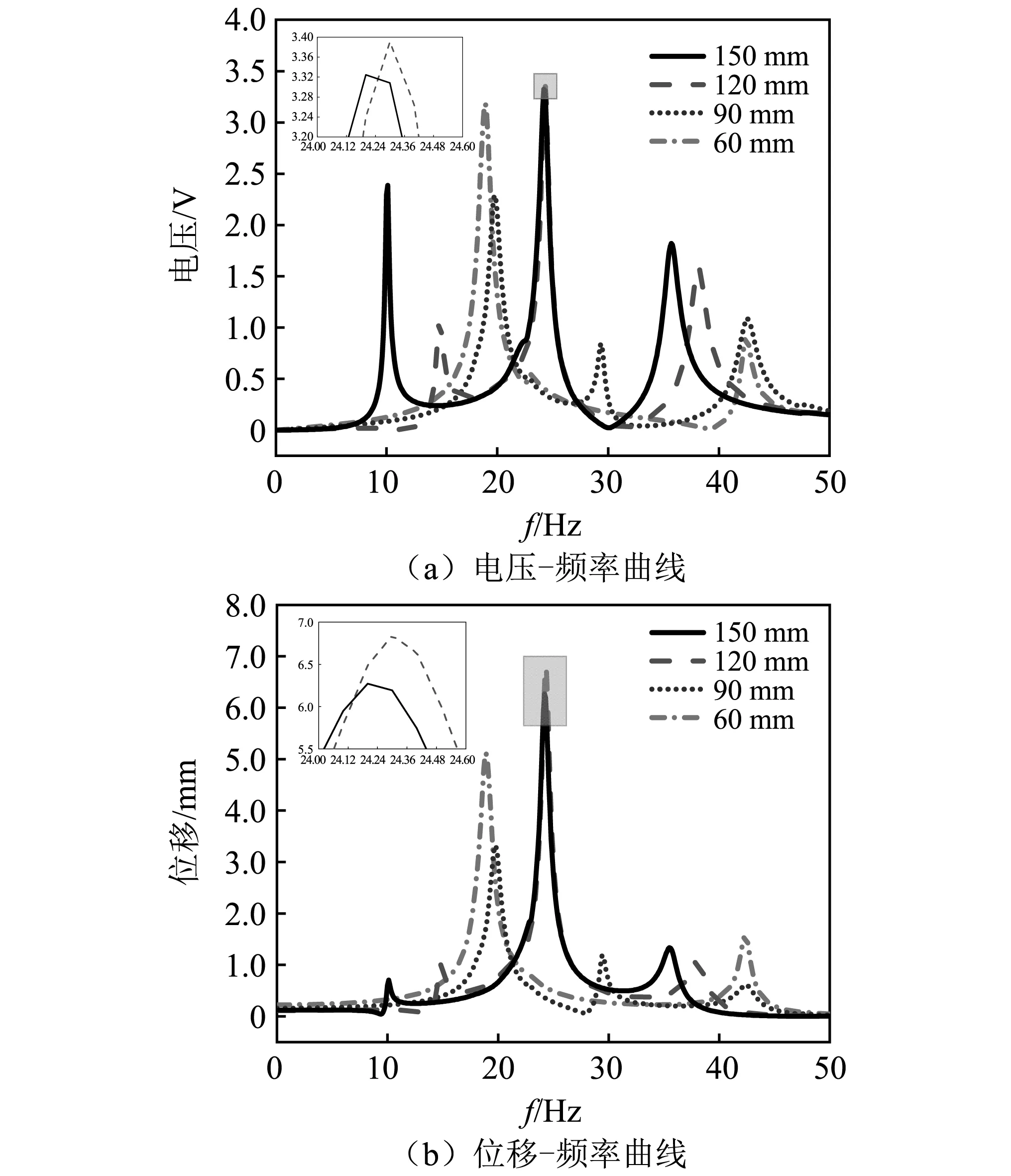
图8 不同第二段梁长度下Z型梁结构电压-频率曲线与自由端位移-频率曲线Fig.8 Voltage and free end displacement frequency curves of Z-shaped beam with different lengths of the second segment beam

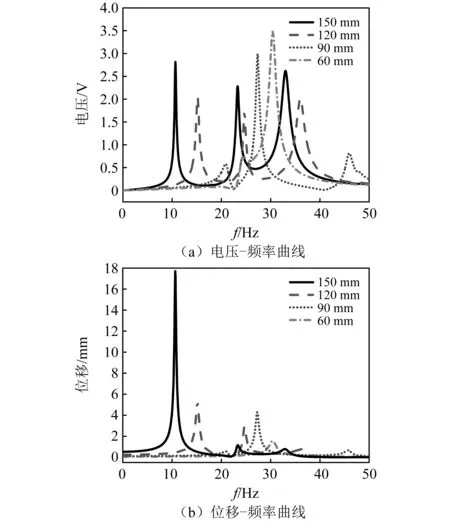
图9 不同第三段梁长度下Z型梁结构电压-频率曲线与自由端位移-频率曲线Fig.9 Voltage and free end displacement frequency curves of Z-shaped beam with different lengths of the third segment beam

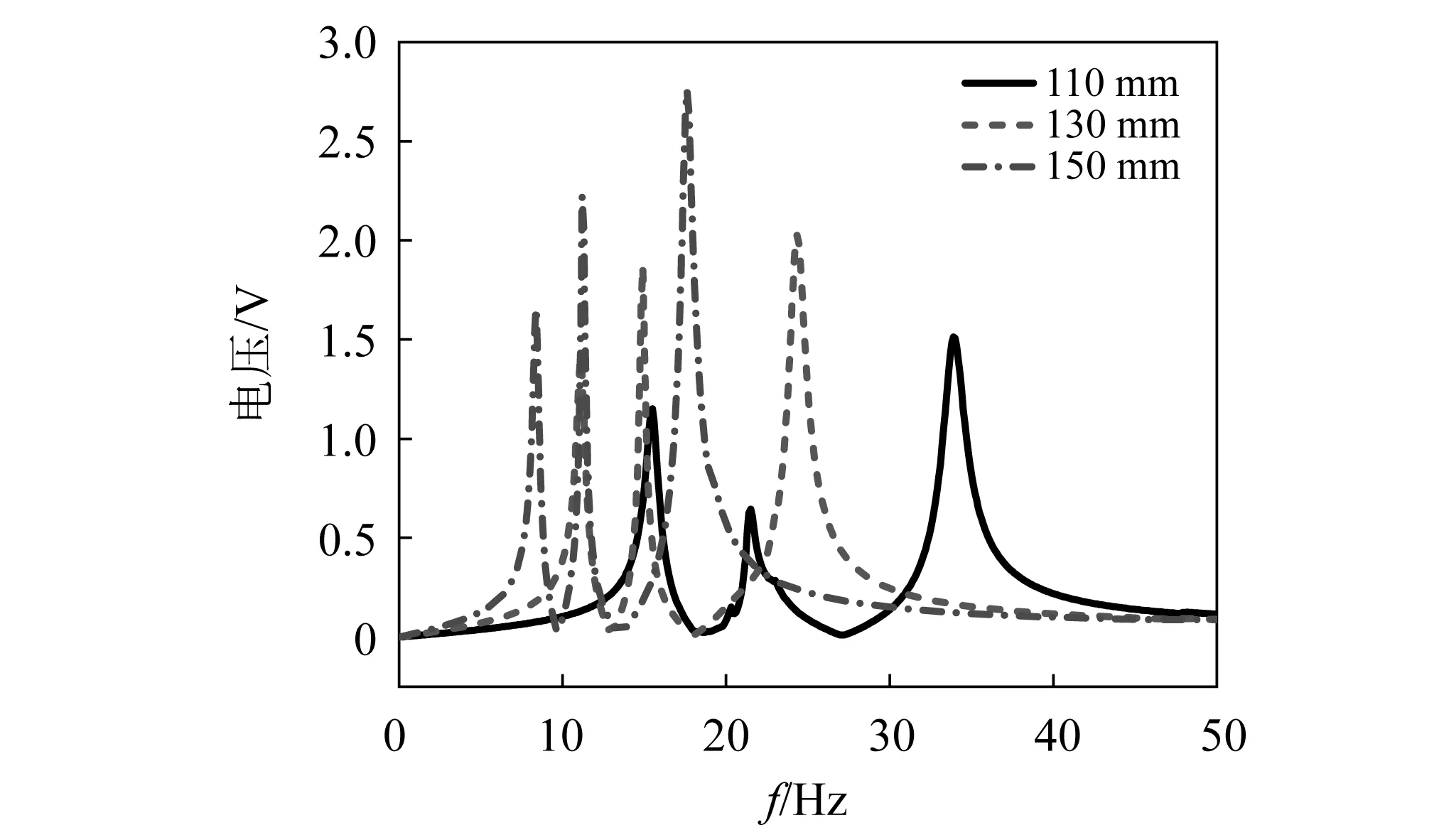
图10 三段梁长度同时变化下的Z型梁结构电压-频率曲线Fig.10 Voltage frequency curve of Z-shaped beam structure with three beam lengths changing at the same time

图11(a)为第二段梁厚度变化下Z型梁结构电压-频率曲线。随第二段梁厚度的增大，第一阶固有频率发生较小偏移，第二阶固有频率明显增大。随着第二段梁厚度的增大，一、二阶电压峰值明显增大，三阶电压峰值减小。位移随梁厚度的变化规律与电压随梁厚度的变化趋势基本一致，但第二阶固有频率附近的自由端位移变小。当第二段梁厚度由0.6 mm增加至0.8 mm时第二阶电压的变化差远大于厚度由0.8 mm增加至1.2 mm时电压的变化差。此外，随着厚度的增加，一、二阶固有频率之间非共振带处的电压值不断增加，有效拓宽了工作频率范围。在1.2 mm厚度的情况下，以0.5 V为有效输出电压，工作频带可达17.4～36.3 Hz。如图12所示为第三段梁厚度变化下Z型梁结构电压-频率曲线与自由端位移-频率曲线，随着厚度的增加，各阶固有频率均降低，此外一阶电压峰值略微降低，二阶电压峰值不断增加，三阶电压峰值变化不大，自由端位移随厚度的变化趋势与电压随厚度的变化趋势一致。通过分析Z型梁的结构尺寸，梁长度对压电能量采集性能起主导作用，影响较为复杂。随着第二段梁厚度的增加，第一、第二阶固有频率之间非共振带处的电压值不断增加，有效拓宽了工作频率范围，由此说明可通过合理优化尺寸结构设计不同多模态、宽频的Z型梁结构能量采集器。

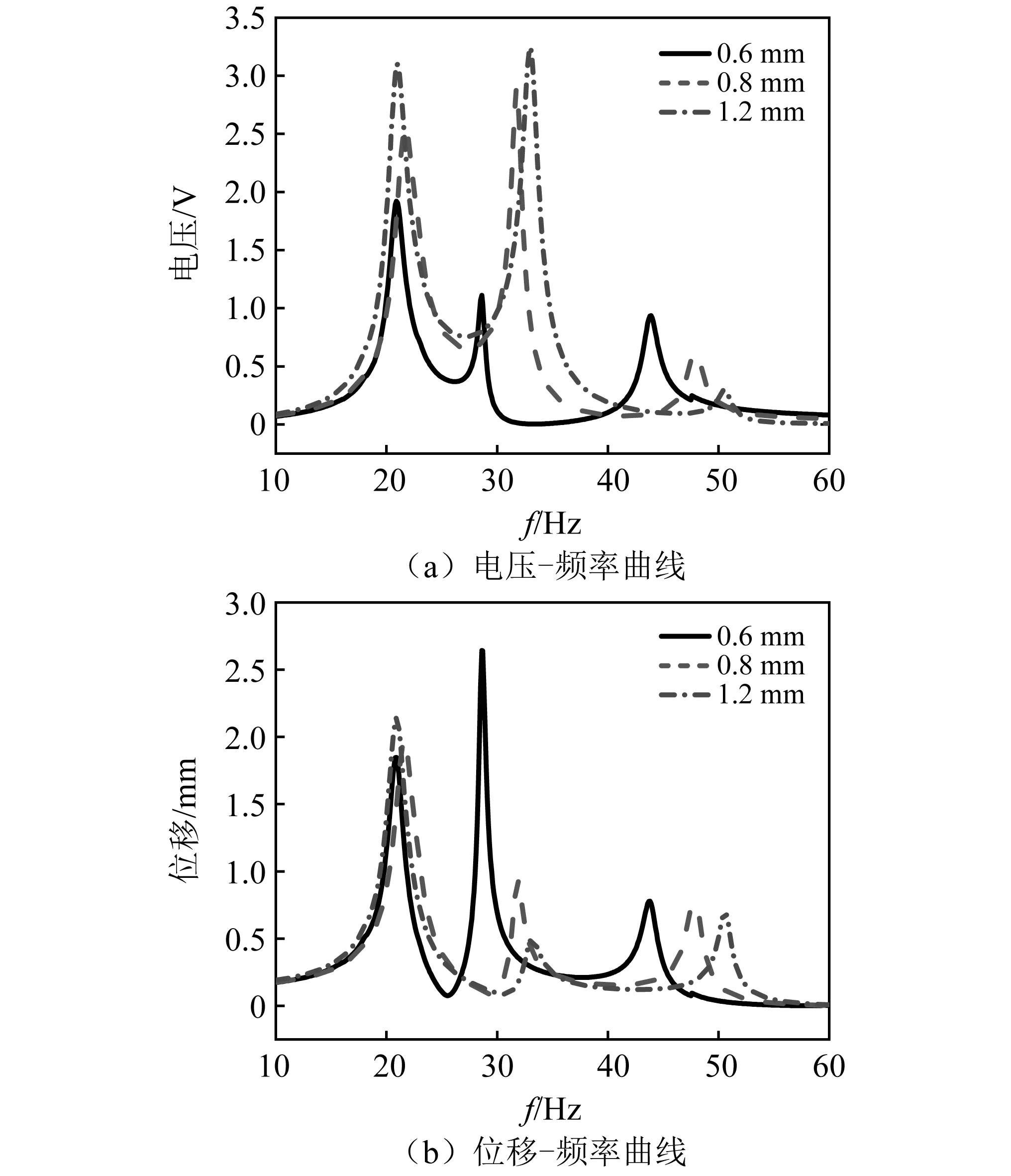
图11 不同第二段梁厚度下Z型梁结构电压-频率曲线与自由端位移-频率曲线Fig.11 Voltage and free end displacement frequency curves of Z-shaped beam with different thickness of the second segment beam

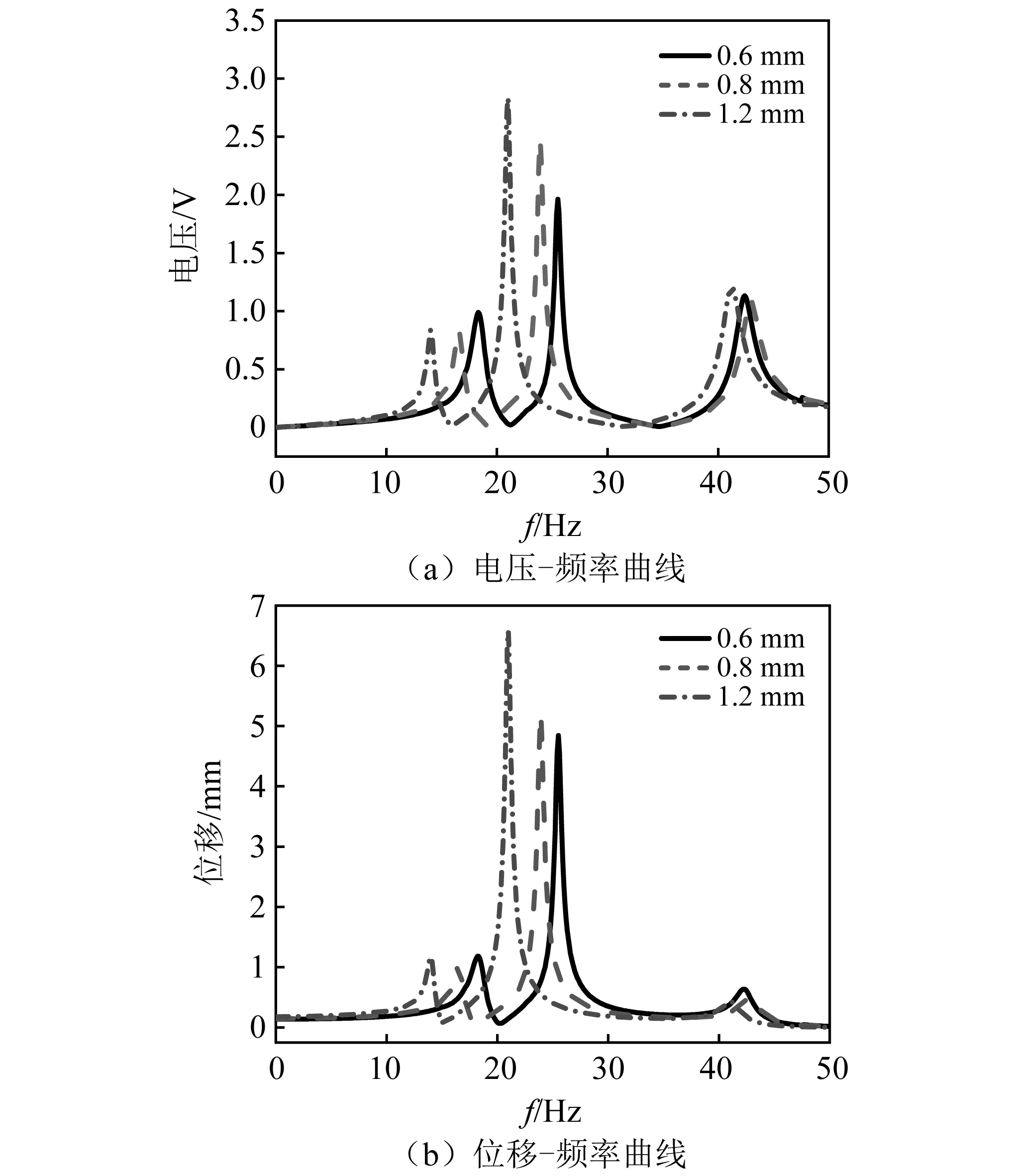
图12 不同第三段梁厚度下Z型梁结构电压-频率曲线与自由端位移-频率曲线Fig.12 Voltage and free end displacement frequency curves of Z-shaped beam with different thickness of the third segment beam

图13为不同激励加速度下Z型梁结构电压-频率曲线与功率-频率曲线。如图13(a)所示，Z型梁结构在不同激励基座加速度作用下的电压响应随加速度的增大而增加。在0.8g的基座加速度下，90°折角Z型梁的一阶电压响应峰值可以达到14 V，同时图13(b)中输出电功率最大可达7.89 mW。在保持0.2g基座加速度的情况下，不同方向激励下Z型梁电压-频率曲线,如图14所示。相较于相近尺寸的传统压电悬臂梁[22]在1g基座加速度下纵向振动产生最大电压约为1.6 V，Z型梁结构对横向激励和纵向激励均有较高的电压响应。

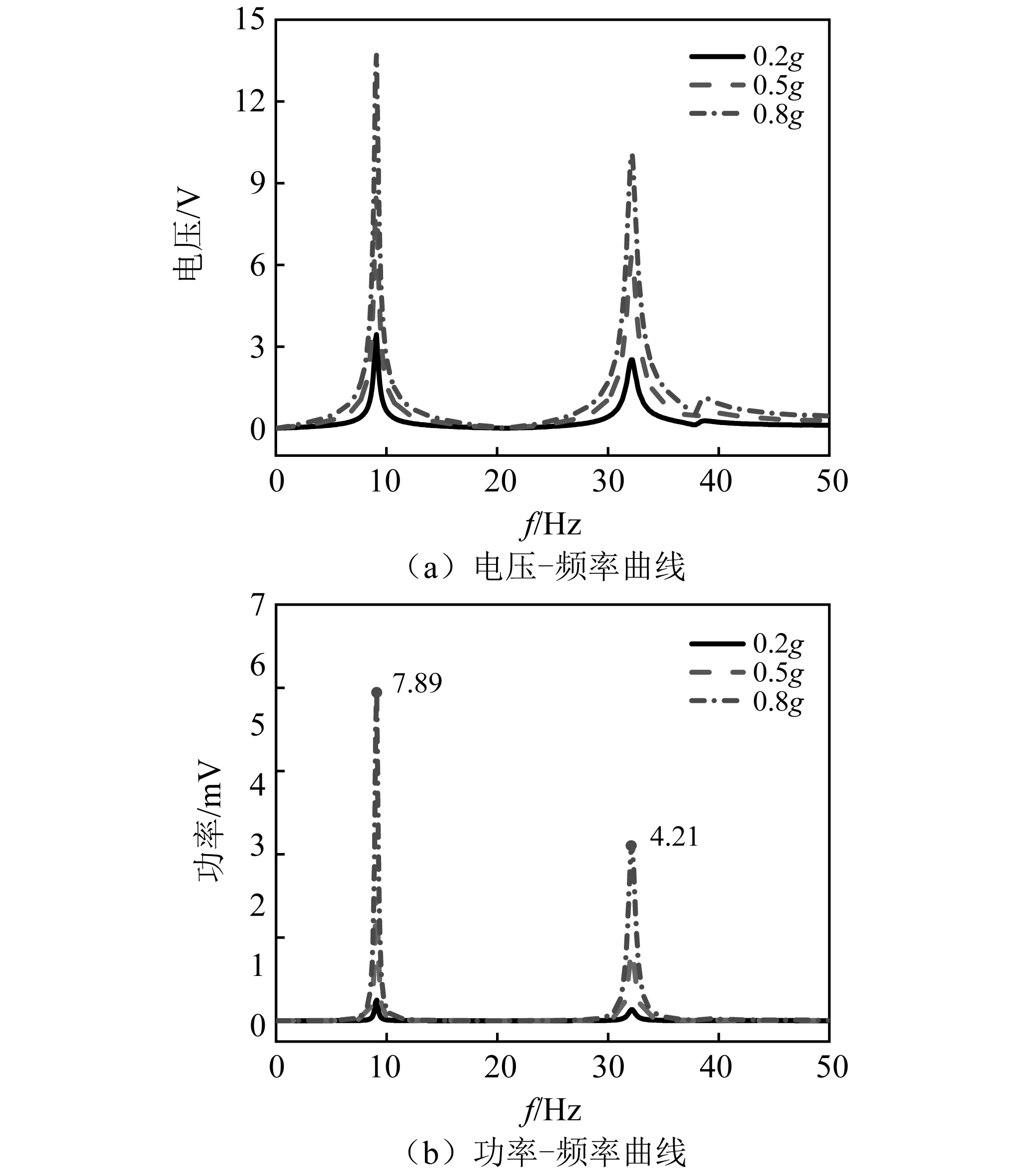
图13 不同激励加速度下Z型梁结构电压-频率曲线与功率-频率曲线Fig.13 Voltage and power frequency curves of Z-shaped beam under different excitation accelerations

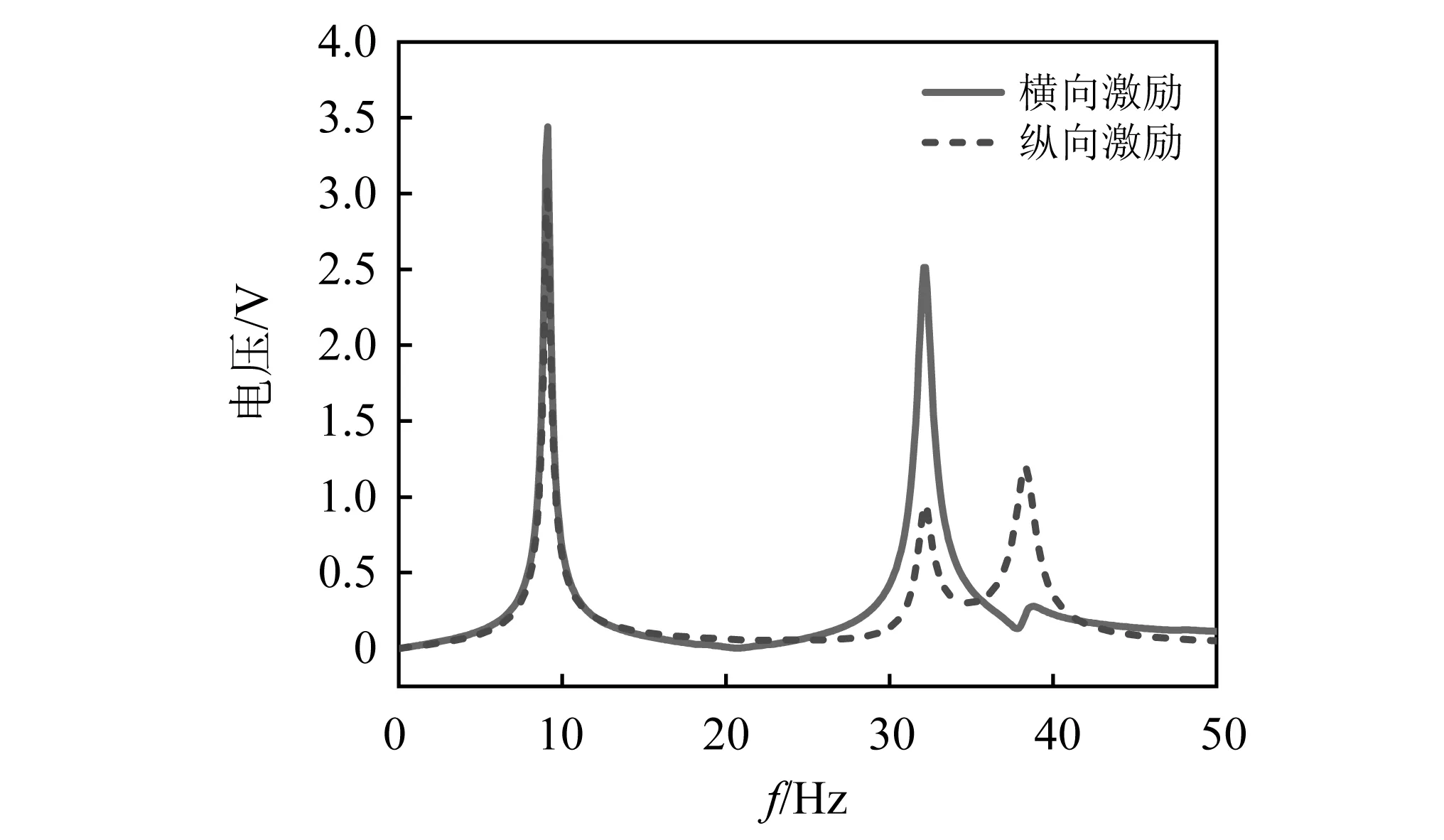
图14 不同激励方向下Z型梁结构电压-频率曲线Fig.14 Voltage frequency curves of Z-shaped beam under different excitation directions

图15为不同外接电阻下Z型梁结构功率-电阻曲线，分别讨论了30°和90°两种结构折角下的能量采集性能。如图15所示，不同固有频率下的能量采集最大功率对应不同的外接电阻。如图15(a)所示，在0.2g的基座加速度下，90° Z型梁结构在第一阶固有频率处的最优电阻解约为12 kΩ，产生的最大功率为0.52 mW；在第二阶固有频率处的最优电阻解约为18 kΩ，产生的最大功率为0.27 mW，而在第三阶固有频率处的功率几乎为零。如图15(b)所示，在0.2g基座加速度下，30° Z型梁结构的前三阶固有频率均存在有效功率，对应的最优电阻分别为8 kΩ，22 kΩ，12 kΩ，产生的最大功率分别为0.05 mW，0.09 mW，0.11 mW。

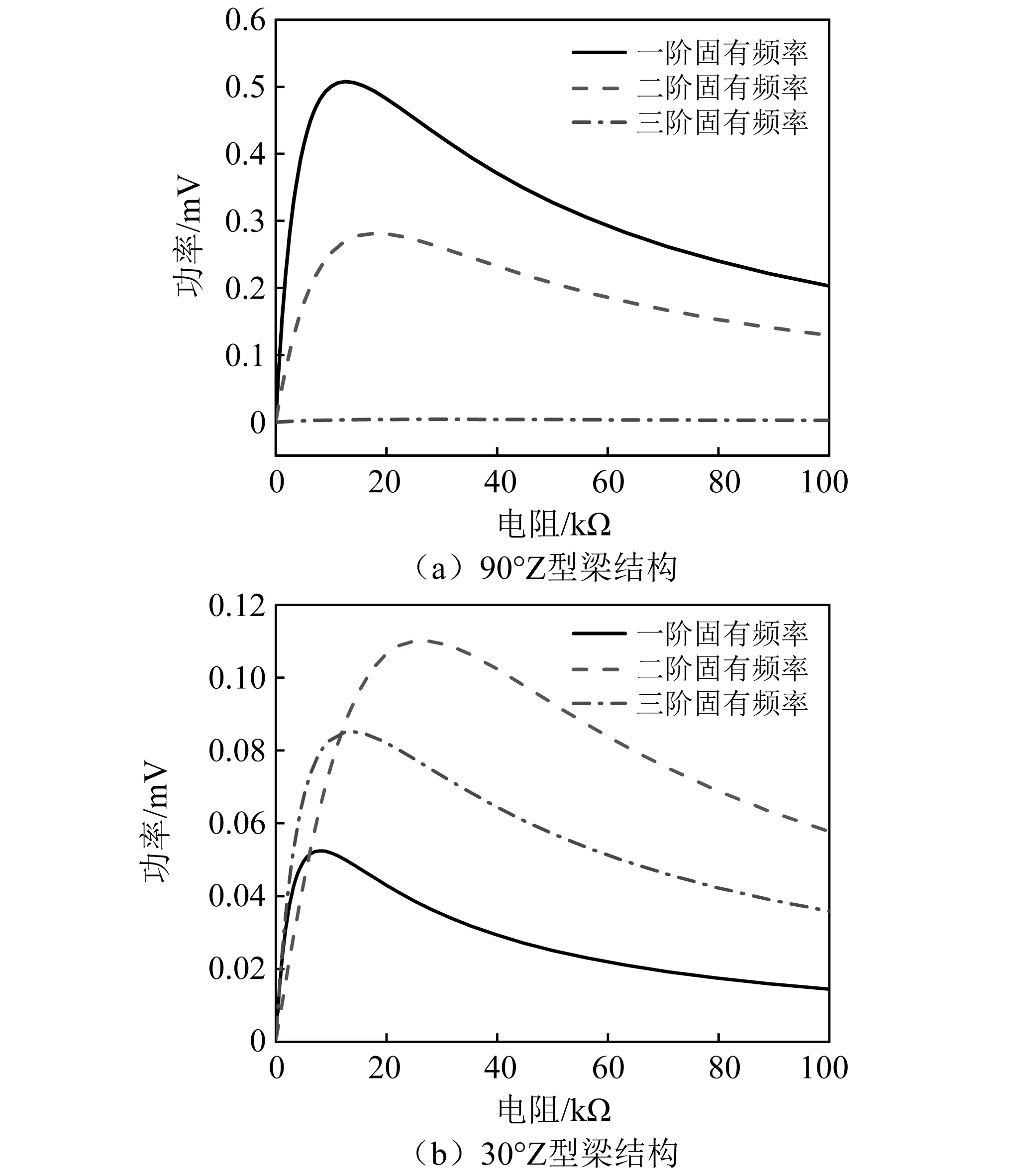
图15 不同外接电阻下Z型梁结构功率-电阻曲线Fig.15 Voltage frequency curves of Z-shaped beam under different excitation directions

4 结 论

本文提出了一种Z型梁结构压电式振动能量采集器，通过理论分析计算了Z型梁折角变化对结构固有频率的影响规律，并采用有限元方法验证了理论分析的准确性和压电能量采集性能，分析结果表明：

(1)该Z型梁结构可实现更多模态共振频率下的有效能量采集。相较于同尺寸结构压电悬臂梁，设计折角0～90°的Z型梁结构，控制频率范围在0～50 Hz，能够实现三个模态共振频率下的稳定电压采集。

(2)该Z型梁结构可实现较为宽频的能量采集。在第二段梁厚度为1.2 mm，保持有效电压采集在0.5 V以上时，工作频带可达17.4～36.3 Hz。

(3)该Z型梁结构可实现不同激励方向的有效能量采集。相较于相近尺寸的传统压电悬臂梁，设计折角为90°的Z型梁结构对横向激励和纵向激励均有较高的电压响应。

(4)该Z型梁结构具有较高电压和功率的能量采集性能。在设计折角为90°、保持0.2g基座加速度作用下时，该结构一阶模态下的最优电阻解约12 kΩ，功率可达0.52 mW。在基座加速度为0.8g时，一阶模态下采集的电压峰值可达14 V，输出电功率可达7.89 mW，同时可保持二阶模态采集的电压峰值在10 V以上。

此外，在后续研究工作中将考虑结构的几何非线性，理论分析几何非线性引起的非线性问题。