整车电磁混合主动悬架故障诊断与容错控制研究

寇发荣， 武江浩, 许家楠， 陈若晨

(西安科技大学 机械工程学院， 西安 710054)

主动悬架能够实现对悬架阻尼和刚度的调节，提升车辆的舒适性与操纵稳定性，成为悬架领域的研究热点[1-3]。但是，对于主动悬架的研究大多数是在各部件完好条件下进行的，主要集中在算法优化、能量回收、特性分析等方面，对其容错控制的研究比较缺乏[4-6]。当悬架作动器发生故障后，不能提供足够的作动力，对车辆的安全性造成威胁[7-9]。

容错控制是指某一悬架作动器发生故障后，通过故障诊断与隔离，判断哪个作动器发生故障，控制器对该故障作动器进行实时力补偿[10-12]。Sun等[13]针对主动悬架作动器故障，提出了一种基于二阶滑模控制的容错控制方法，通过仿真验证了该方法对悬架故障具有鲁棒性，提升了车辆性能。高振刚等[14]在整车模型的基础上，设计了故障诊断观测器实现对作动器在线故障估计，得出容错控制下各作动器的补偿阻尼力。姚行艳[15]针对半主动悬架增益故障，提出了基于自适应模糊控制的汽车半主动悬架容错控制。杨柳青[16]通过鲁棒观测器对悬架故障在线诊断基础上，设计了基于控制率重组的容错控制器，消除了作动器故障影响。但目前对悬架容错控制的研究大多是基于1/4车辆进行的，对整车悬架故障诊断与容错控制的研究较少。

本文基于电磁混合作动器(electro-magnetic linear hybrid actuator，EMLHA)的主动悬架，设计整车电磁混合主动悬架容错控制策略。建立整车7自由度模型，采用LQG控制器作为EMLHA悬架的常规控制器。针对悬架的某一作动器发生故障，提出一种主动容错控制方法。该方法以未知输入观测器获得悬架动挠度残差，通过逻辑模块和稳定模块联合判定哪一作动器发生故障，对其进行实时力补偿，实现容错控制。最后，开展了仿真分析与台架试验，验证了该容错控制的有效性与可行性。

1 EMLHA工作原理与故障分析

电磁直线混合作动器(包括直线电机和电磁阀两部分),如图1所示。该作动器主要包括上吊耳、永磁体、节流口、电磁阀、活塞、液压油等。直线电机部分工作在馈能状态时，车身振动带动直线电机做切割磁感线运动产生电能，可通过储能装置将电能回收。直线电机部分工作在主动状态时，可以通过调节直线电机的输入电流，输出相应的控制力。电磁阀部分工作时，可以通过调节节流口的开度实现阻尼力的调节。

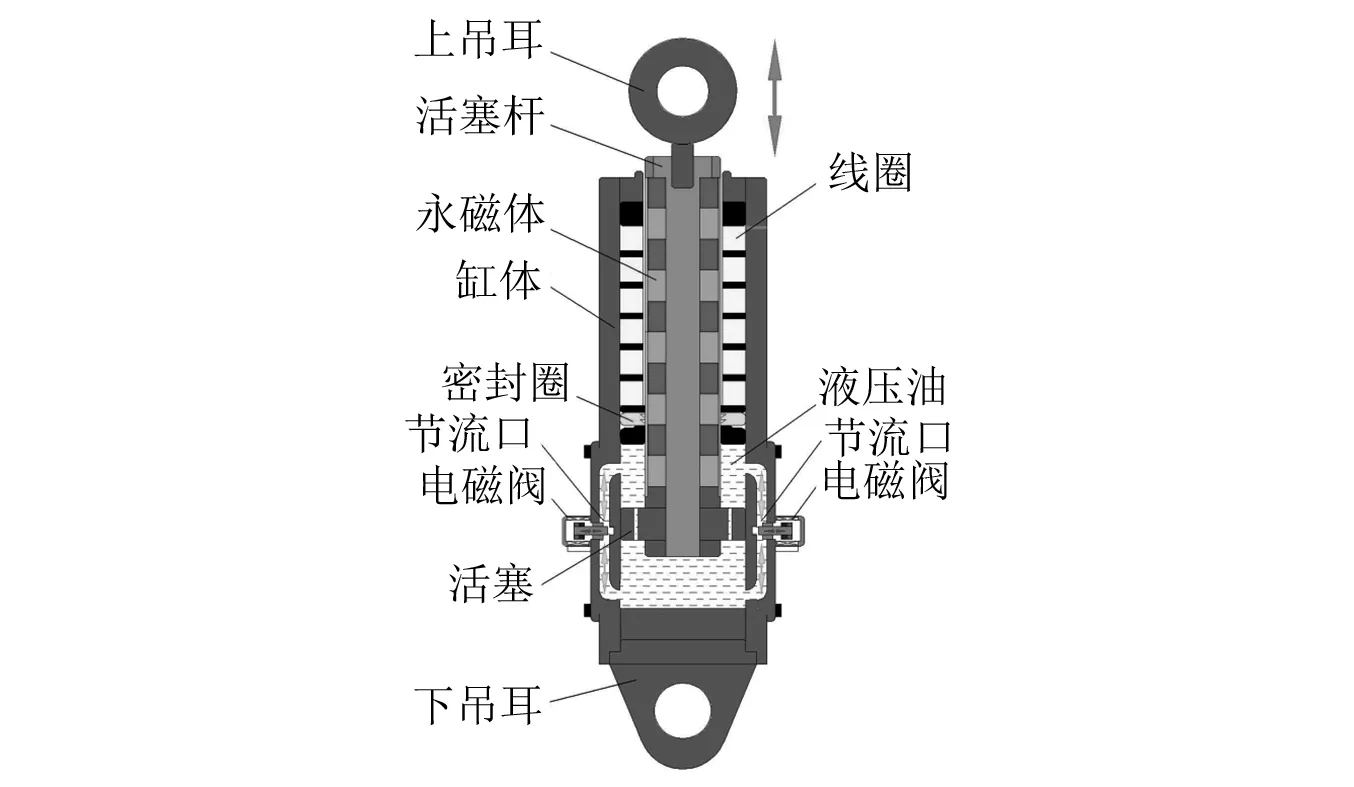
图1 EMLHA结构图Fig.1 Structure diagram of EMLHA

悬架作动器是保障车辆行驶平顺性与操纵稳定性的重要部件。长期的使用过程中，由于零件磨损、油液变质等可能会导致作动器出现故障。结合电磁混合悬架作动器结构，对该作动器常见的故障进行分析：①由于电磁阀的油液泄露或者直线电机漏磁现象引起的增益故障；②由于电磁干扰引起电磁阀阀芯位移偏差，导致的恒偏差故障；③由于液压油高温烧结或者直线电机活塞杆受热膨胀，引起的卡死故障。

2 悬架系统动力学模型

为了能够更加准确的仿真整车的实际振动，建立整车7自由度模型如图2所示。

图2 整车7自由度悬架模型Fig.2 Seven degree of freedom suspension model of vehicle

整车的车身垂向、俯仰、侧倾的运动学方程分别为[17]

(1)

(2)

(3)

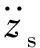
非簧载质量垂向运动方程为

(4)

其中,

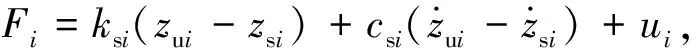
选取该悬架系统的状态变量为X、干扰输入为W、控制输入为U、控制输出为Z，得到整车7自由度悬架状态空间方程为

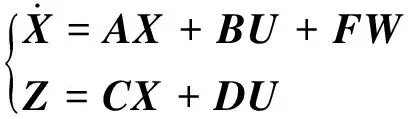
(5)

其中,

W=[zg1zg2zg3zg4]T,

U=[u1u2u3u4]T,

式中：zsui为悬架动挠度，zsui=zsi-zui；A为14×14维矩阵；B为14×4维矩阵；C为7×14维矩阵；D为7×4维矩阵；F为14×4维矩阵。

3 电磁混合主动悬架容错控制

3.1 LQG控制器设计

LQG控制器的的控制目标是提高车辆的操纵稳定性与平顺性。为了更好的降低车辆的车身垂向加速度、俯仰角加速度、侧倾角加速度、悬架动挠度、轮胎动变形，并且使所需控制力最小，降低能耗。定义主动悬架的线性二次型综合性能指标泛函如下[18]

(6)

式中：q1为车身垂向加速度加权系数；q2为车身俯仰角加速度加权系数；q3为车身侧倾角加速度加权系数；q4,q5,q6,q7为悬架动挠度加权系数；q8,q9,q10,q11为轮胎动变形加权系数；q12,q13,q14,q15为可控力加权系数；Q为状态加权矩阵；R为控制加权矩阵。

将线性二次型指标泛函J改为矩阵形式为

(7)

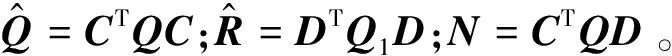
根据最优控制理论得最优控制规律为

U=-KX(t)

(8)

式中,K=R-1(BTP+NT)为反馈增益矩阵,P为修正Ricatti方程的解。

3.2 悬架故障建模

根据对悬架作动器故障的分析，当整车电磁混合主动悬架的第j个作动器发生故障时，建立如下故障模型

ufj=Δjuj+αj

(9)

式中：ufj为有故障时作动器输出；uj为无故障时作动器输出；αj为作动器卡死位置值或恒偏差值；Δj为作动器故障增益系数。当Δj∈(0,1),αj=0时，为增益故障；当Δj=0,αj≠0时，为卡死故障；当Δj=1,αj≠0时，为恒偏差故障。

电磁混合主动悬架系统故障输出Uf

(10)

令

(11)

则

Uf=U+Fa

(12)

在故障状态下，电磁混合主动悬架状态空间方程为

(13)

发生故障时的残差为

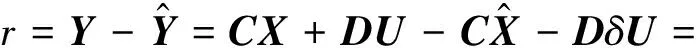
(14)

本文只对悬架发生增益故障进行分析，当某一悬架发生故障后，悬架作动器的输出力简化为

ufj=Δjuj

(15)

悬架的补偿力为

Fj=(1-Δj)uj

(16)

3.3 故障检测与隔离

基于观测器的悬架故障诊断方法，是利用悬架系统的可测信息对无故障状态下的输出进行估计。通过观测器重构后的状态观测变量与可测的实际变量做差值，构成残差序列，从残差序列中把故障检测与隔离。由于路面干扰是随机的，本文采用未知输入观测器对悬架进行状态观测，其全阶未知输入观测器结构[19]为

(17)

(18)

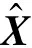
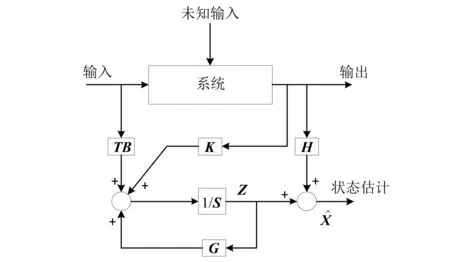
图3 未知输入观测器结构图Fig.3 Structure of UIO

观测器的状态误差向量为

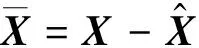
(19)

输出估计残差为

(20)

状态误差向量的控制方程为

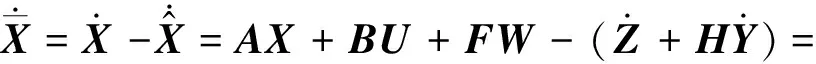
(21)

式中：I为适维矩阵；K=K1+K2。

当式(18)满足条件式(19)时

(22)

根据所得的悬架动挠度残差rsu，对悬架系统进行故障诊断，故障诊断结构图如图4所示。

图4 故障诊断框图Fig.4 Fault diagnosis structure diagram

当有悬架作动器发生故障时，未知输入观测器可以计算得到四个悬架动挠度的残差rsui，将四个悬架动挠度残差值rsui输入到逻辑判断模块，由于故障作动器的悬架动挠度残差大于无故障作动器的悬架动挠度残差，经过逻辑判断模块比较四个悬架动挠度大小后，可判定哪个作动器发生故障，将该故障作动器的悬架动挠度残差输入到稳定模块，稳定模块判定该故障稳定存在后，LQG控制器为故障作动器提供补偿控制力，实现电磁混合悬架系统的容错控制。

3.4 逻辑判断模块设计

本文只考虑一个悬架作动器发生故障的状况，为了在悬架作动器发生故障后能够判断是几号作动器发生的故障，设计了逻辑判断模块进行判断。逻辑判断框图如图5所示。

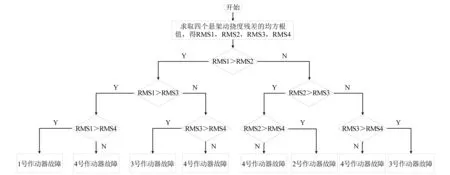
图5 逻辑判断框图Fig.5 Logic judgment block diagram

将四个悬架动挠度残差rsu1,rsu2,rsu3,rsu4输入到逻辑判断模块，并求取其均方根值RMS1,RMS2,RMS3,RMS4,依次比较四个均方根值的大小，均方根值最大的说明该悬架作动器发生故障。

3.5 稳定模块设计

由于路面凸块等会对悬架产生冲击，可能导致悬架瞬时故障。为了避免瞬时故障状态时悬架系统产生误判，对悬架进行过度力补偿，导致悬架系统紊乱，能源浪费，设计了一种稳定模块，提高了悬架对故障判断的可靠性。稳定模块流程如图6所示。

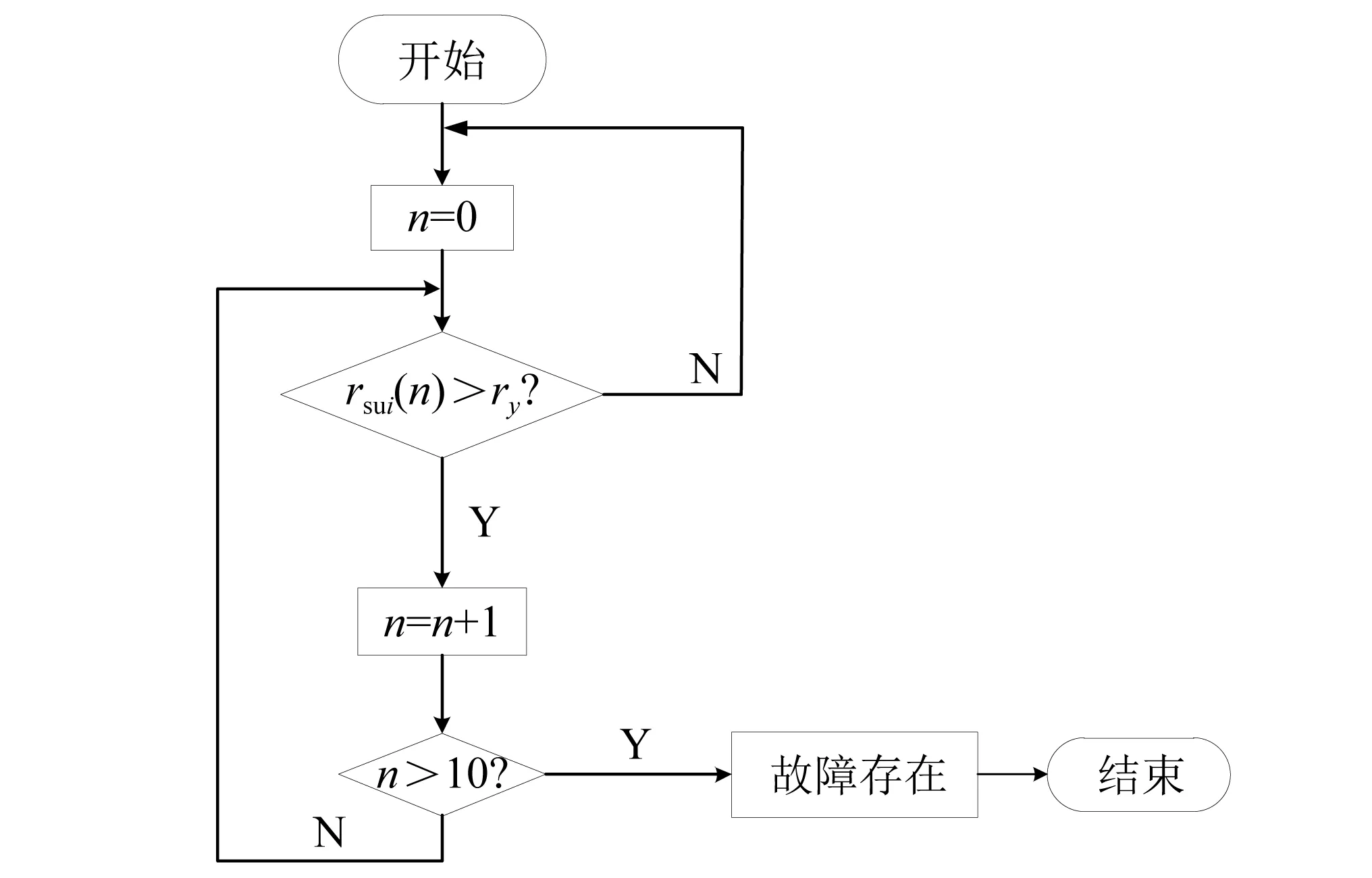
图6 稳定模块流程图Fig.6 Flow chart of stability module

经过逻辑判断模块判定后，将该故障作动器的悬架动挠度残差rsui输入到稳定模块，如果连续10次所得到的残差都大于设定的悬架动挠度残差阈值ry，那么确定该作动器发生故障，通过LQG控制器进行力补偿,若其中一次悬架动挠度残差不超过阈值ry，则重新开始采样，直到满足条件才对作动器进行力补偿。

4 仿真分析

为了验证所设计的整车电磁混合悬架容错控制策略的正确性，在MATLAB/Simulink环境下建立电磁混合悬架的仿真模型，悬架系统的参数如表1所示。

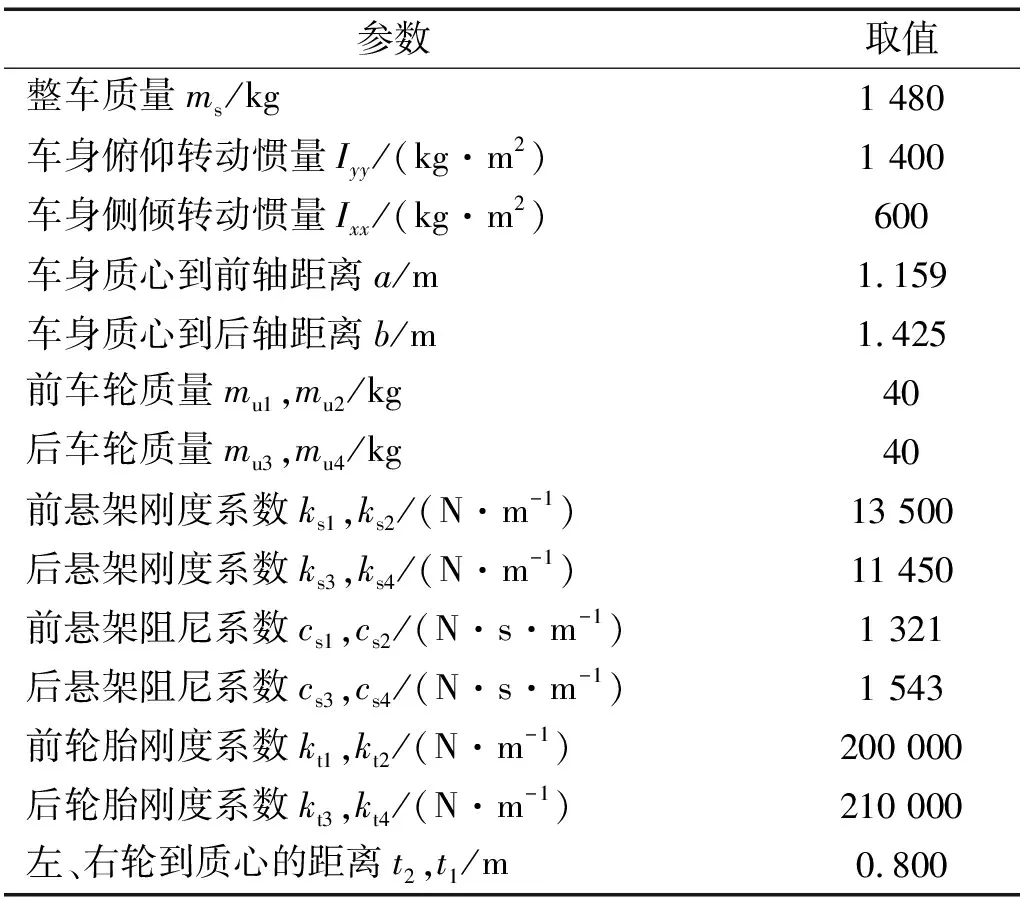
表1 悬架系统参数

4.1 未知输入观测器仿真分析

设定仿真在车速为70 km/h，B级路面下进行，仿真时间为5 s，对悬架状态的实际值以及采用UIO状态估计下的状态估计值进行对比。对比结果如图7所示。四项悬架性能指标均方根值对比，如表2所示。

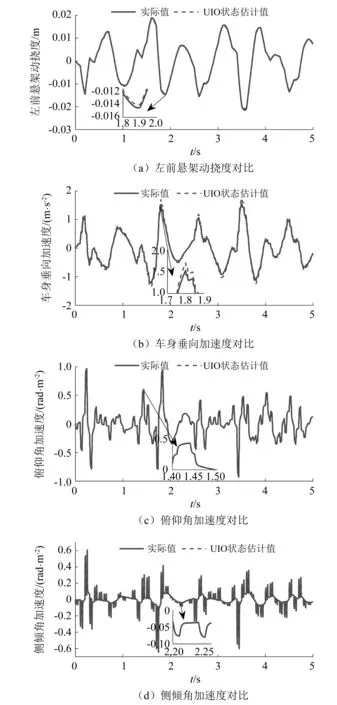
图7 悬架状态估计值对比Fig.7 Comparison of suspension state estimation

表2 悬架性能指标均方根值

根据表2所示，左前悬架动挠度的状态估计误差为2.800%，车身垂向加速度误差为6.109%，俯仰角加速度误差为1.976%，侧倾角加速度误差为2.950%。四项性能指标的状态估计误差均较小，在合理范围内，表明未知输入观测器的状态估计效果较为准确。

4.2 故障诊断仿真分析

为了验证作动器发生故障后，所设计的故障诊断方法能够准确的判断故障来源，在MATLABSimulink环境下建立了整车电磁混合悬架的故障诊断模型,对增益故障情况下进行仿真分析。

设定左前悬架在5 s时发生0.4倍增益故障，仿真在车速为70 km/h，B级路面下进行，仿真时间共10 s。得出各悬架的悬架动挠度残差，通过所设计的故障诊断模块对哪一悬架发生故障进行判断。如图8所示为所设置的左前悬架增益故障，图9为发生故障后各架的悬架动挠度残差。

图8 左前悬架增益故障Fig.8 Left front suspension gain fault

图9 悬架动挠度残差Fig.9 Residual of suspension working space

左前悬架动挠度残差均方根值为9.007×10-3m,右前悬架动挠度残差均方根值为3.687×10-3m，左后悬架动挠度残差均方根值为2.467×10-3m,右后悬架动挠度残差均方根值为3.144×10-3m。故障诊断模块根据四个悬架动挠度的均方根值得出左前悬架动挠度残差的均方根值最大，将该信号输入到稳定模块，连续采样10次的悬架动挠度残差都超过了阈值，判定其发生故障。

4.3 容错控制仿真分析

为了验证所设计容错控制的有效性，分别对LQG控制下的正常状态，发生故障后的故障状态，以及故障进行容错控制后的悬架性能进行对比。悬架的性能对比图如图10所示。对左前悬架在5 s时设置0.4倍增益故障，设定仿真在车速为70 km/h，B级路面下进行，仿真时间共10 s。

图10 悬架性能对比Fig.10 Comparison of suspension performance

由表3可知，在0～10 s内，左前悬架动挠度容错效果(容错控制状态与故障状态相比)为58.717%，车身垂向加速度容错效果为32.498%，俯仰角加速度容错效果为35.850%，侧倾角加速度容错效果为34.560%。根据仿真结果，在所设计的容错控制策略下，整车电磁混合悬架的性能指标得到提升，改善了车辆平顺性与操纵稳定性同时，安全性也得到保障，表明该容错控制策略具有有效性。

表3 不同状态下悬架性能指标均方根值

4.4 频域分析

为了从频域角度分析该容错控制的效果，对三种状态下的左前悬架动挠度、车身垂向加速度、俯仰角加速度、侧倾角加速度进行快速傅里叶变换，得到相应的功率谱密度，如图11所示。

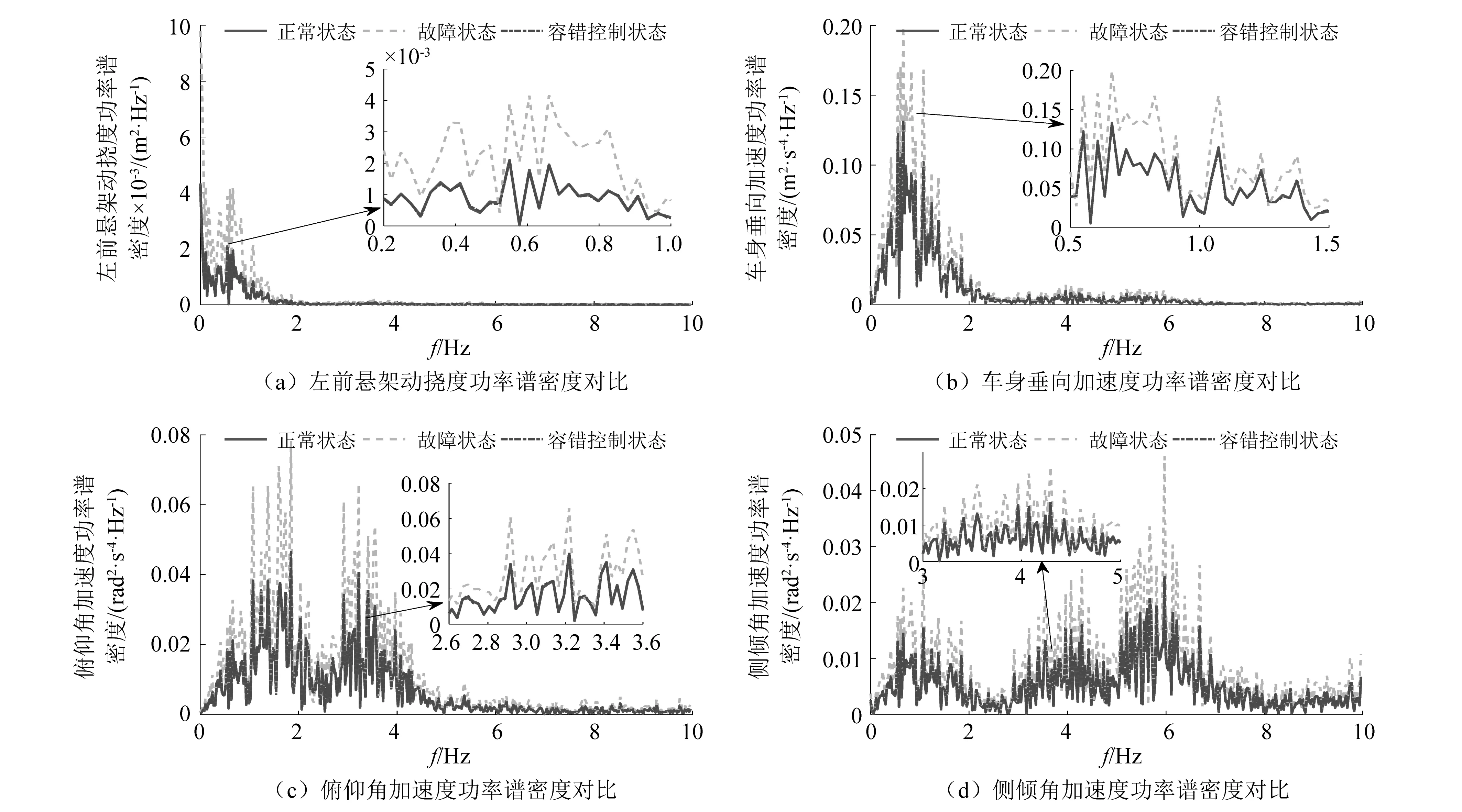
图11 不同状态下悬架性能指标功率谱密度对比Fig.11 Comparison of power spectral density of suspension performance index under different states

由图11可知，在频率为0～10 Hz内，在容错控制状态下整车电磁混合悬架系统的四项性能指标的功率谱密度相比故障状态下大幅降低，并且最终趋向于平稳。在车身共振频率1.0～1.5 Hz以及人体最敏感的频率范围4.0～12.5 Hz内[20]，功率谱密度显著降低，可以减小路面冲击对车身以及人体脏器官的损害。

5 实车试验

为了验证所设计的整车电磁混合悬架容错控制的正确性，对所设计的容错控制进行了整车试验。试验的设备如图12所示，包括试验车、电磁混合悬架、位移传感器、DSPACE、上位机、数据采集仪、驱动模块、加速度传感器等。

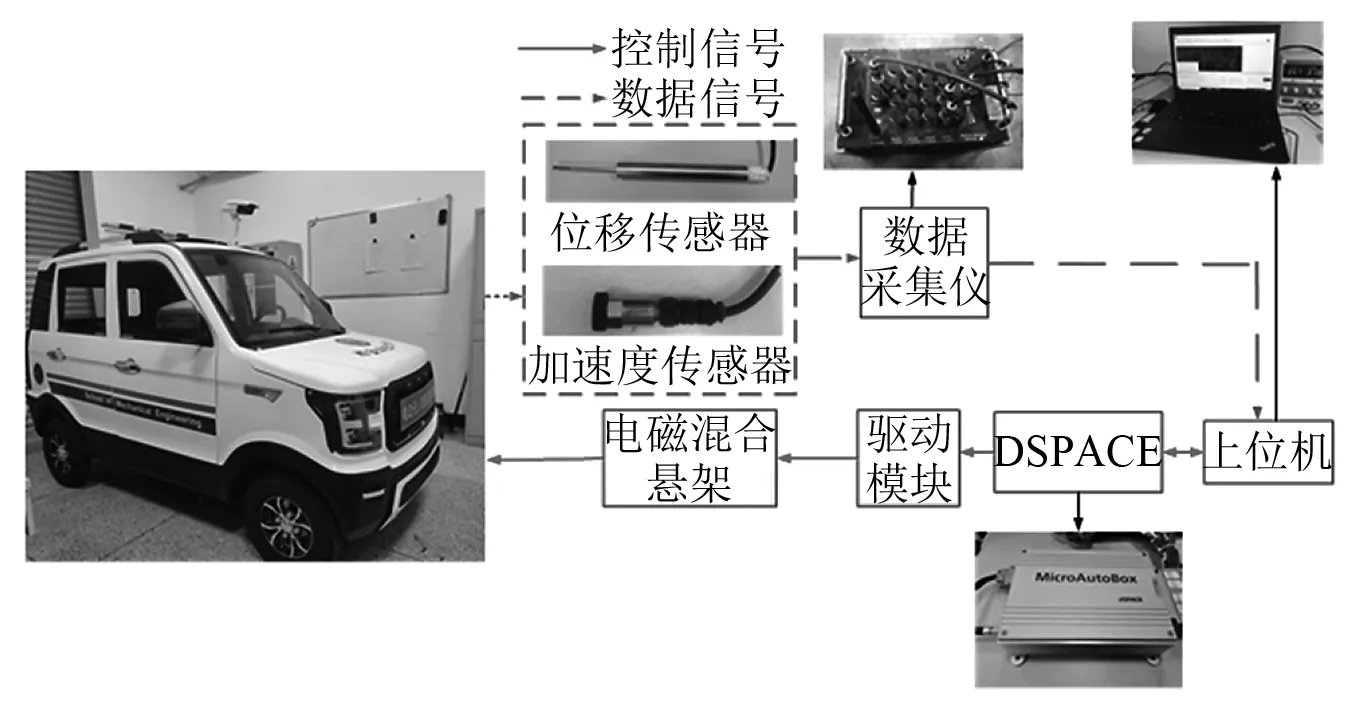
图12 试验系统结构示意图Fig.12 Schematic diagram of test system structure

通过DSPACE对电磁混合悬架的输入电流进行控制，从而调节电磁混合悬架的控制力。初始时刻，控制输入电流为10 A,电磁混合悬架工作在正常状态，在t=6 s时，改变左前悬架输入电流为5 A，悬架所提供的作动力不足，以此模仿电磁混合悬架处于故障状态，进行试验。四个位移传感器将采集的悬架动挠度信号进行对比，判断哪个悬架发生故障，对其进行力补偿，整个试验过程持续12 s。由于试验条件的限制，只对左前悬架动挠度和车身垂向加速度进行对比，试验结果如图13和图14所示。

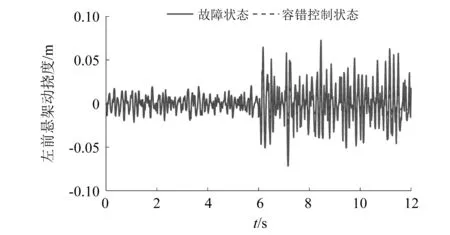
图13 左前悬架动挠度试验对比Fig.13 Test comparison of left-front suspension working space

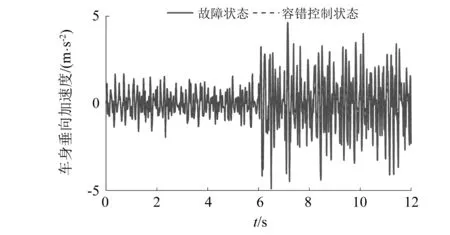
图14 车身垂向加速度试验对比Fig.14 Test comparison of vehicle body vertical acceleration

根据试验结果，在第6秒发生故障后，容错控制使故障悬架性能经过短暂时滞后性能得到提升。在故障状态下，电磁混合悬架左前悬架动挠度均方根值为1.788×10-2m，在容错控制状态下，左前悬架动挠度均方根值为1.006×10-2m，相比故障状态降低了43.736%。在故障状态下，电磁混合悬架车身垂向加速度均方根值为1.230 m/s2，在容错控制状态下，车身垂向加速度均方根值为0.734 m/s2，相比故障状态降低了40.325%。电磁混合悬架在发生故障时，通过容错控制策略实时控制，悬架的安全性与舒适性得到了提高。

6 结 论

(1)针对整车电磁混合主动悬架的某一作动器发生故障，提出了一种故障诊断与容错控制方法。通过未知输入观测器对悬架进行状态估计，根据获取的悬架动挠度残差信息，在逻辑模块与稳定模块的联合判定下，对悬架作动器故障做出判断并对故障悬架进行力补偿。

(2)利用MATLABSimulink软件对所设计的故障诊断与容错控制方法进行仿真分析，结果表明：在容错控制下，左前悬架动挠度容错效果为58.717%，车身垂向加速度容错效果为32.498%，俯仰角加速度容错效果为35.850%，侧倾角加速度容错效果为34.560%。

(3)最后开展了整车电磁混合悬架容错控制实车试验，分析了左前悬架动挠度与车身垂向加速度的改善效果，验证了该方法的可行性。