受饱和约束的车辆转向非线性鲁棒模糊分布控制

孙船斌， 方 琳， 童宝宏,2

(1.安徽工业大学 机械工程学院， 安徽 马鞍山 243032；2.安徽工业大学 低碳与智能车辆研究所， 安徽 马鞍山 243032；3.安徽工业大学 特种重载机器人安徽省重点实验室， 安徽 马鞍山 243032)

驾驶员面临高速行驶的紧急避障，操纵方向盘通常会在短时间达到极限位置，从而使车辆处于急转向过程，在此期间轮胎力学特性由线性状态迅速进入饱和非线性状态，导致车辆转向出现侧滑和侧倾失控的危险极限状态。极限状态下车辆的横摆-侧倾运动是强非线性耦合过程，需要协同考虑横摆-侧倾稳定控制，提高非线性扰动下车辆极限工况的稳定安全性。目前研究多单独针对极限工况下的操纵稳定性或侧翻稳定性，对车辆横摆和侧倾稳定性的综合研究较少。金辉等[1]利用质心侧偏角相轨迹进行极限车速稳定性控制。李绍松等[2]对极限工况下主动前轮转向汽车进行稳定性控制。李道飞等[3]基于最优轮胎力分配对车辆动力学集成控制。

在众多主动控制策略中，鲁棒控制策略对非线性扰动具有很好的控制效果。张家旭等[4]对带参数摄动的车辆底盘的集成鲁棒混合控制研究，将轮胎侧偏刚度非线性视为小扰动。胡延平等[5]针对非线性干扰设计了基于输出反馈的非线性H∞控制，改善线性控制器的控制效果。朱天军等[6]基于线性矩阵不等式的重型车辆防侧翻鲁棒控制算法研究，将转向角作为非线性扰动进行稳定控制。极限状态下车辆的轮胎力和悬架力处于剧烈变化的非线性状态，如何在控制过程实时、准确地反映车辆非线性，是本文鲁棒控制考虑的一个重要问题。

此外，本文研究主动前轮转向(active front steering, AFS)和直接横摆力矩控制(direct yaw-moment control,DYC)的集成控制，综合考虑了前轮转向执行限制和轮胎附着极限引起的输入饱和约束。文献[7]为提高多轮轮毂电机驱动车辆动力学综合控制性能，利用趋近率获取滑模SMC期望控制反馈，将执行分配问题转换为二次规划问题进行求解。李静等[8]研究新的状态反馈的鲁棒L2-L∞/H∞控制方法，在转向约束和悬架力分配的基础上，协调主动前轮转向系统和主动悬架系统的控制输入。MPC控制能够处理多约束问题，但复杂的实时矩阵运算会增加硬件成本，而且硬约束无法实时保证系统最优问题可解，文献[9]利用MPC研究路面附着极限横向轨迹跟踪控制，引入松弛变量来弱化安全约束所施加的硬约束。软约束能提高系统求解可行性，但忽略反馈输入受饱和约束的影响，可能会引起系统性能恶化，这也是本文控制关注的另一个重要问题。

针对上述问题，本文采用AFS+DYC对极限状态车辆横摆侧倾稳定性控制。首先利用Takagi-Sugeno(T-S)方法实时逼近极限工况下动态非线性，建立车辆横摆侧倾模型和改进横摆参考模型。引入输入约束松弛因子提高执行器利用率，同时考虑反馈输入受到饱和约束后对控制系统的影响，将其作为有界扰动进行控制。构建T-S框架下主动前轮输入的动态饱和阈值，采用范数有界的侧翻稳定阈作为侧倾性能约束，协调AFS和DYC集成控制。基于分布补偿结构(parallel distributed compensation,PDC)设计状态反馈模糊控制器PDC-TS，并将车辆横摆-侧倾非线性鲁棒H∞控制转换为线性矩阵不等式LMIs凸优化问题。最后基于Trucksim-MATLAB/Labview进行控制仿真测试和硬件在环验证，对比传统鲁棒控制、无控制工况车辆的极限转向过程，并分析松弛因子对控制过程的影响。

1 车辆Takagi-Sugeno模糊模型

1.1 非线性模型

选取质心较高的中型车辆作为横摆-侧倾控制对象，车辆横摆-侧倾模型如图1所示。车辆转向过程前进速度vx不变，假设车身侧倾中心在转向过程中不变。车辆横摆-侧倾耦合运动模型如式(1)，fd为车身的侧向惯性力矩。极限状态下横摆运动过程中，前后轮侧偏力是侧偏角的非线性函数，忽略两侧转向差异，轮胎侧偏力可以表示为Fyf=Cf(α1)α1,Fyr=Cr(α2)α2，其中Cf(t),Cr(t)为轮胎等效侧偏刚度。侧倾过程的悬架输出力是侧倾角θ和侧倾角速度p的非线性函数，刚度kx(t)、阻尼cx(t)均为时变非线性。文中主要参数如表1所示。

表1 仿真模型主要参数

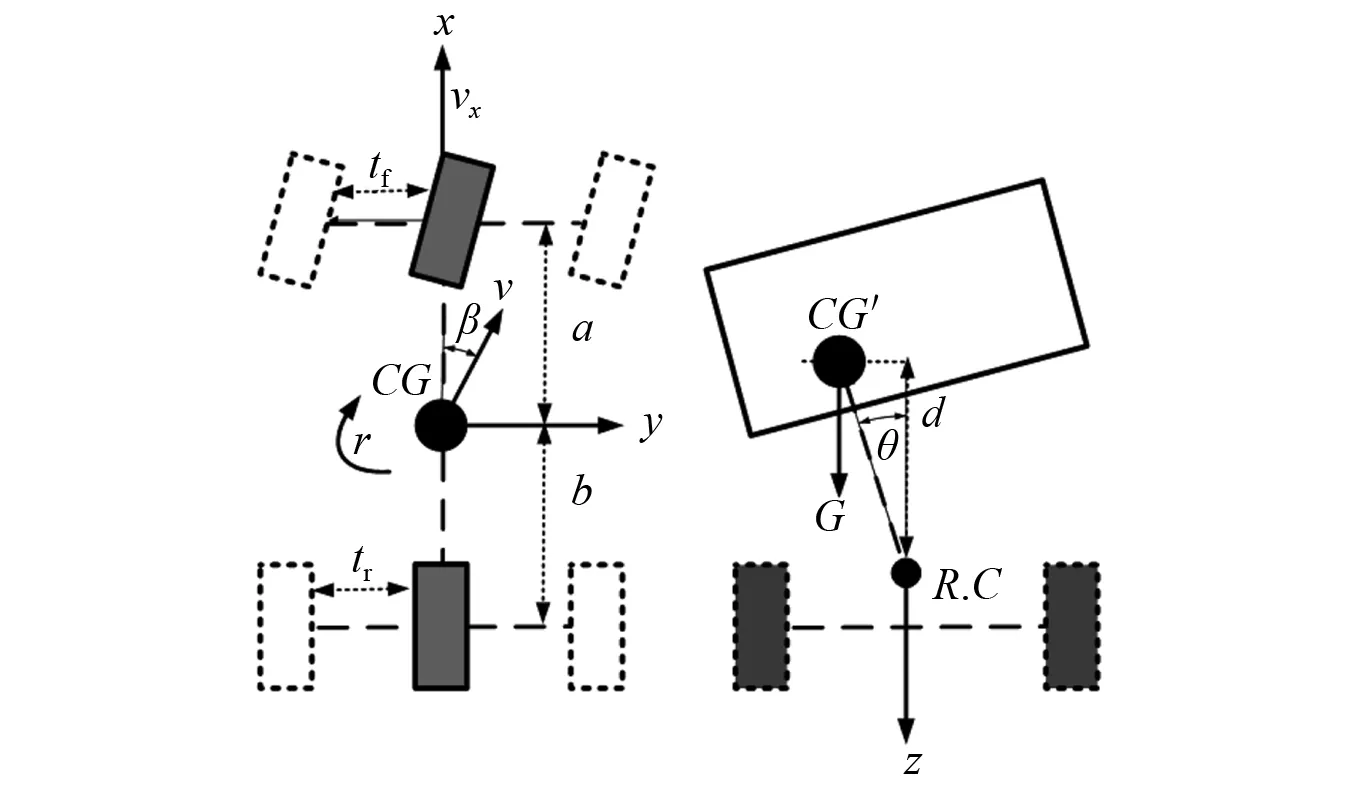
图1 车辆横摆-侧倾模型Fig.1 Yaw-roll model of vehicle

(1)

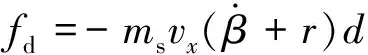
(2)

文中控制输入Uδ为主动前轮转向角预期增量Δδf产生的附加前轮侧偏力。为减轻转向轮胎操纵负担，减少制动对纵向车速的影响，本文直接横摆力矩Mdyc通过制动单侧后轮得到[10]。

1.2 动态参数模糊观测器

在式(1)中，轮胎力和悬架力分别是轮胎侧偏角和侧倾状态的非线性函数。在正常稳定行驶过程中，轮胎和悬架均可看作处于线性区域，极限工况会导致车辆状态往非线性区域变化。需要一个过渡区域，兼顾线性与非线性的平衡，如图2所示。在此非线性工作域内，轮胎侧偏力和悬架输出力均在扇形域内变化。在此扇形域，轮胎侧偏刚度Cf,r、悬架侧倾刚度kx和阻尼系数cx均在一定范围内连续变化。在轮胎力与悬架力的扇形域，可以通过T-S方法逼近非线性车辆模型。

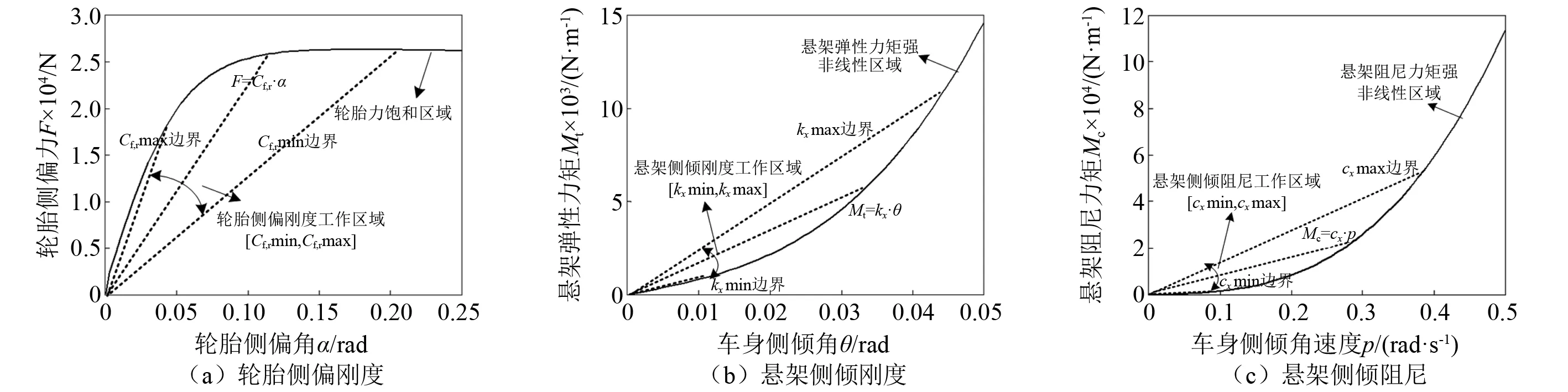
图2 轮胎与悬架的扇形工作域Fig.2 Sector area of tire and suspension

在扇形工作域内，轮胎侧偏刚度随轮胎侧偏角连续变化，悬架侧倾刚度和阻尼则随车身侧倾角、角速度连续变化。前后轮胎侧偏角由式(3)得到

(3)

将前后轮侧偏角、车身侧倾角和角速度作为输入，通过轮胎和悬架模型动态参数的模糊观测器，实时观测车辆前后轮的非线性侧偏刚度、车身侧倾非线性刚度和阻尼。模糊观测器如图3所示，其中轮胎与悬架模型参数随观测输入的变化规律并不一致，归一化处理时区别对待。通过对模糊观测器参数的调整，能够尽可能地逼近真实状态[11-12]。

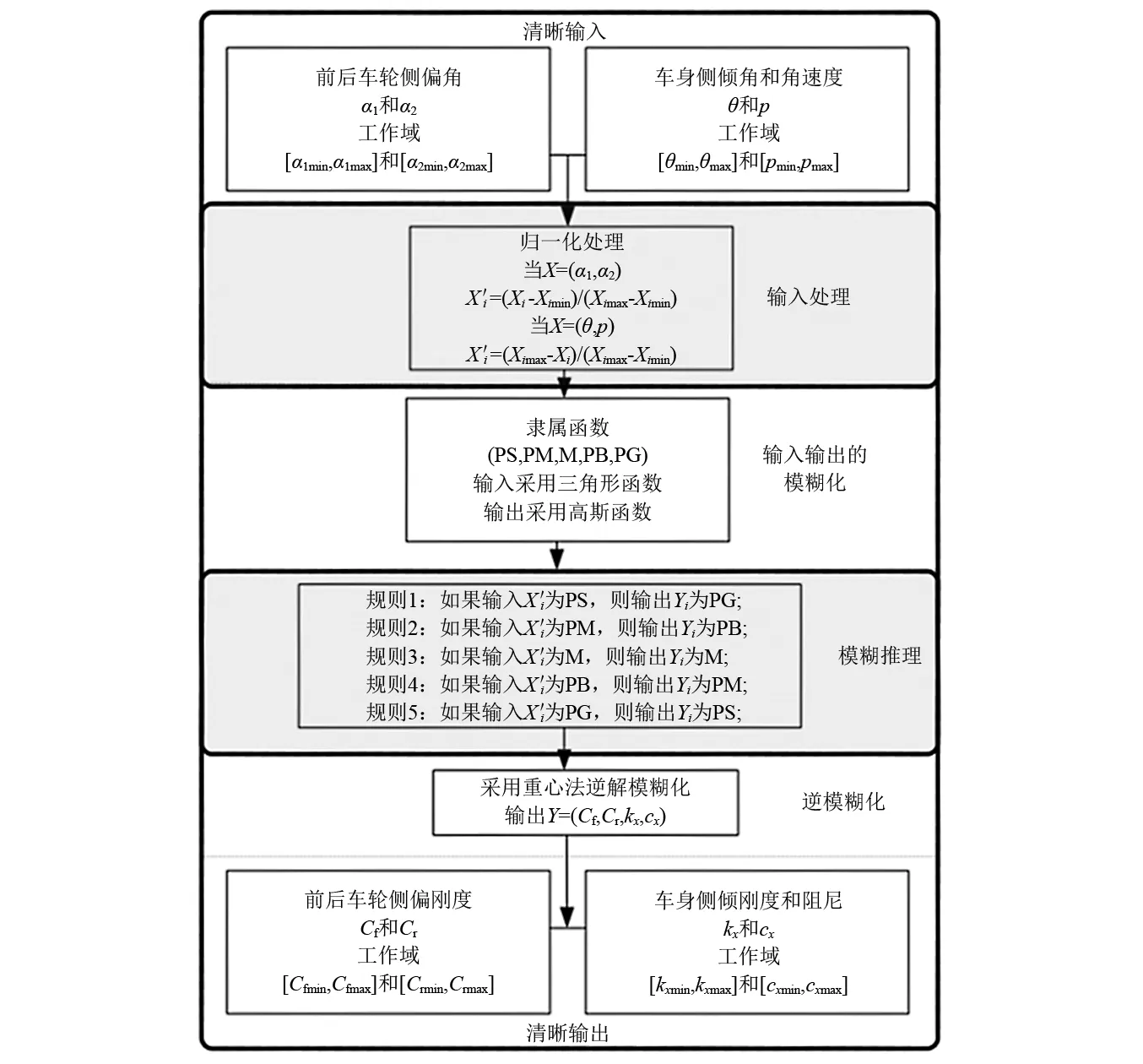
图3 动态参数模糊观测器Fig.3 Fuzzy observer for dynamic parameters

1.3 基于模糊观测的T-S车辆模型

结合图3动态参数模糊观测器，利用观测得到轮胎和悬架的动态模型参数，构建由16个子系统构成的T-S车辆模型如式(4)，将前轮转角δ作为扰动

(4)

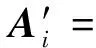
(5)

16个线性子系统的车辆模型规则如下：

IFξ=[CfiCrikxicxi] isMi;

具体规则如表2所示，其中PB和PS分别表示大(max)和小(min)。在具体规则编号i，Mi(n)将ξ(n)(n=1，2，3，4)对应的ξ(n)min和ξ(n)max代替矩阵Ai′和Ni′的Cfi，Cri，kxi，cxi。

表2 T-S模型模糊规则

式(4)中，结合模糊观测得到的轮胎侧偏刚度Cf,Cr和侧倾刚度kx、阻尼cx，实时更新子系统隶属度hi=G1(Gf)×G2(Cr)×G3(kx)×G4(cx)≥0，且

(6)

模糊规则的隶属度函数如下

IFMi(n) is PB

IFMi(n) is PS

(7)

2 基于PDC的鲁棒模糊控制

2.1 改进期望横摆运动

各条模糊规则下，轮胎侧偏刚度是线性的，根据模糊规则构建T-S框架下车辆横摆运动在稳态下横摆角速度rs如式(8)所示

(8)

式(8)反映当前轮胎非线性下的稳态运动，利用动态参数获取隶属度h函数逼近真实运动，同时隐含了轮胎侧移约束，相比于线性轮胎的横摆稳态更接近于实际情况。

联合式(8)和式(9)得到轮胎非线性下的改进理想横摆运动，引入一阶惯性环节ts得到期望横摆角速度rd状态方程如式(9)所示

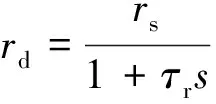
(9)

图4给出了本文方法改进的期望横摆运动，可以看出在Sine with Dwell极限转向输入下，车辆横摆稳态运动已经超出侧滑极限，相较传统方法，T-S方法的横摆参考能够更准确地表现车辆非线性。

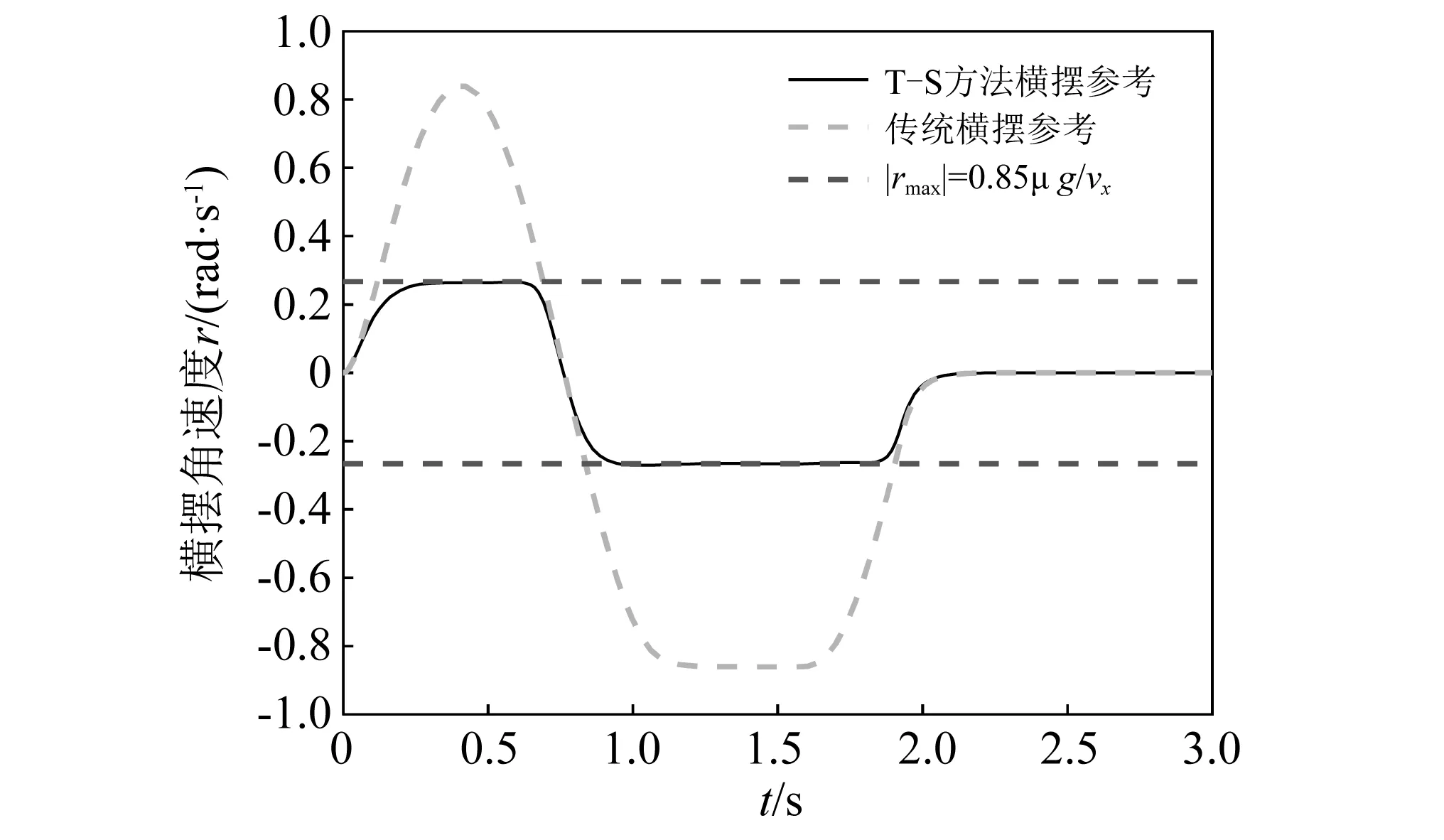
图4 T-S方法期望横摆角速度Fig.4 Desired yaw velocity with T-S method

2.2 T-S框架下动态饱和约束控制模型

结合车辆模糊模型式(4)和期望横摆运动式(9)，将期望横摆运动扩展为系统状态向量，得到T-S框架下16个子系统构成的车辆控制模型式(10)

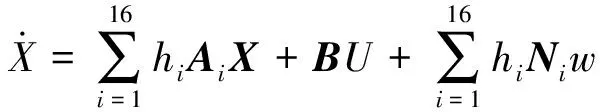
(10)

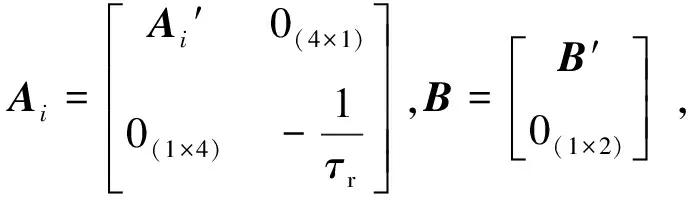
(11)

式(10)中实际控制输入U满足饱和约束

(12)

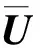
主动前轮转向不仅受到极限执行限制，还受到轮胎侧滑约束。当前轮侧偏刚度处于非线性阶段，较小的主动前轮转角变化容易使轮胎趋于饱和，而前轮处于线性阶段时，较大的前轮转角变化仍然允许。为了适应这种情况，预期的前轮转角增量范围应随轮胎侧偏刚度变化。引入T-S方法设置主动前轮附加力的动态阈值

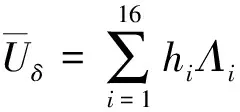
(13)

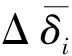
图5给出了本文前轮转向附加侧向力的阈值，根据前轮侧偏刚度的非线性，允许的前轮侧向力阈值也在相应变化。随着车辆进入转向极限状态，动态阈值逐渐减小，限制前轮主动转向产生的侧向力Uδ，而由直接横摆力矩Mdyc作为主要控制输入。这种协同控制过程随着车辆状态变化，相对于传统固定阈值能够更好地改善控制效果。

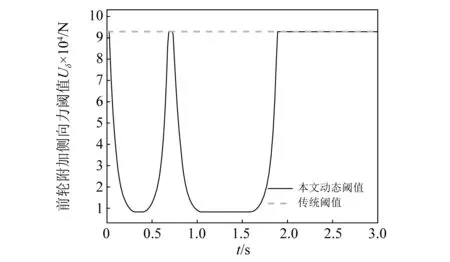
图5 前轮附加侧向力动态阈值Fig.5 Dynamic threshold value of additional lateral force for front wheel

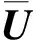
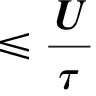
(14)

引用如下不等式[13]用于LMIs推导，‖·‖表示向量或矩阵的2范数

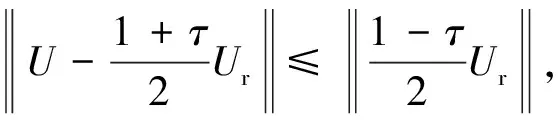
(15)

其中，

(16)

将式(16)引入系统控制式(10)，整理得T-S框架下动态饱和约束控制式(17)

(17)

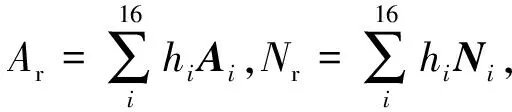
(18)

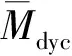
2.3 PDC-TS模糊分布控制

引入分布式补偿控制PDC结构

(19)

式中：Kr为式(17)的状态反馈增益矩阵；Ki为T-S框架下子系统状态反馈增益矩阵，将非线性系统式(17)的控制转化为16个线性子系统反馈增益矩阵的求解，并对子系统隶属度h实时更新。文中假设状态X是已知的，实际可由传感器观测或者估算得到，不作重点讨论。

首先关注紧急转向时车辆横摆稳定性，将横摆运动跟踪误差作为横摆稳定性控制目标

Z1=[βr-rd]T=CX

(20)

此外，极限工况下车辆车身摇摆幅度过大，会降低侧倾稳定性，横向载荷转移率LTR是评价侧倾稳定的常用方法。

Z2=kxθ+cxp=ΦX

(21)

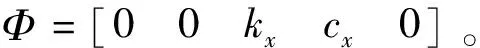
本文通过悬架输出力矩间接得到轮胎两侧载荷转移率，并将悬架系统输出力矩的范数作为侧倾稳定性能约束

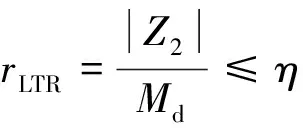
(22)

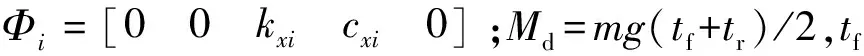
在反馈输入饱和约束式(14)和侧倾性能约束式(22)下，闭环系统式(17)的H∞性能可以通过L2增益表示

(23)

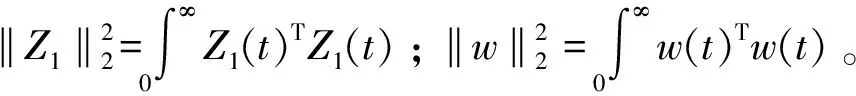
当Ki=YiP，对于零初始条件下的闭环系统式(17)，在方向盘扰动下存在γ>0，0<τ<1，使系统鲁棒控制性能式(23)成立，且满足动态饱和约束式(14)和侧倾稳定约束(22)。其中Yi和P满足矩阵不等式Ψ,Π,Σ，将在下文推导证明。

至此，将鲁棒模糊分布控制器PDC-TS的设计，转化为LMIs最小值问题，引入引理1用于推导。

引理1对于适当维数的任意矩阵(向量)X和Y，存在任意σ>0，以下不等式成立

XTY+YTX≤σXTX+σ-1YTY

(24)

证明推导如下：

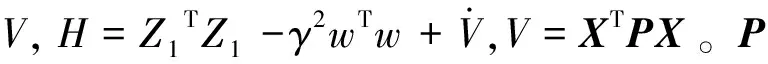
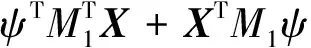
(25)

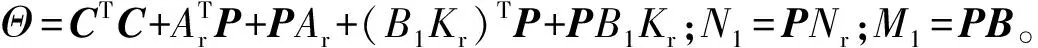
根据引理1式(24)选择常数σ>0，结合不等式(15)，则

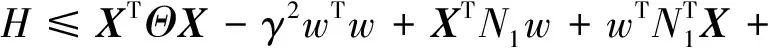
(26)

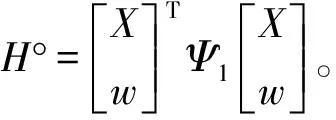
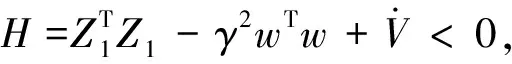
Ψ1=

(27)

将式(27)左乘diag(P-1,I)，右乘它的转置，等价于式(28)

(28)

式中:Q=P-1;Yr=KrQ;Θ°=QArT+ArQ+(B1Yr)T+B1Yr+σ-1BBT。

应用Schur补引理，将非线性不等式(28)转换为线性不等式

(29)

结合式(6)，将系统反馈增益矩阵Kr的求解，转化为子系统反馈增益矩阵Ki。式(29)成立，当不等式(30)满足。

(30)

式中:Θi=QAiT+AiQ+(B1Yi)T+B1Yi+σ-1BBT;Yi=KiQ。

显然地，当‖ΦiX‖≤ηMd满足，侧倾性能约束式(22)成立。根据文献[15]，存在椭圆集XTPX≤ρ，则Φi(P/ρ)-1ΦiT≤η2MdTMd。式(22)等价于

(31)

式中，Φ°i=ΦiQ。

同理，对于动态饱和约束式(14)

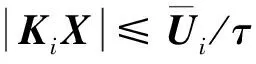
(32)

需要注意的是，当式(32)满足，反馈输入动态饱和约束(14)成立，而式(16)和式(17)则保证实际输入满足饱和约束式(12)。结合XTPX≤ρ，对于控制向量的2个元素

(33)

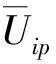
综合式(30)、式(31)和式(33)，将闭环系统式(17)的动态饱和约束非线性鲁棒控制问题，转换为凸优化问题：

Minγsubject to LMIsΨandΠandΣ。

线性不等式LMIs通过MATLAB线下求解，得到16个子系统的状态反馈控制Ui=KiX。结合模糊观测器在线观测车辆的非线性轮胎和悬架参数，实时计算隶属度函数h。结合式(19)获取PDC-TS反馈输入Ur=KrX，并根据约束式(12)得到实际控制输入U。由于子系统控制反馈矩阵并不需要实时计算，在一定程度上降低了控制器硬件性能要求，并提高控制器运行效率。本文鲁棒模糊分布控制器PDC-TS的控制流程，如图6所示。

图6 模糊分布控制PDC-TS控制流程Fig.6 Flow of fuzzy distributed control PDC-TS

3 结果分析

采用Sine with Dwell转向输入使车辆达到极限状态，模拟正常行驶车辆突然避障的实际场景，如图7所示。前进车速恒定为vx=80 km/h，路面摩擦因数μ=0.8，联合Trucksim-MATLAB中进行PDC-TS控制仿真。以质心侧偏角、横摆角速度、车身侧倾角和横向载荷转移率LTR为指标，对比传统鲁棒控制、无控制车辆极限工况稳定性，并分析模糊分布控制PDC-TS松弛因子τ=1和0<τ<1的结果。

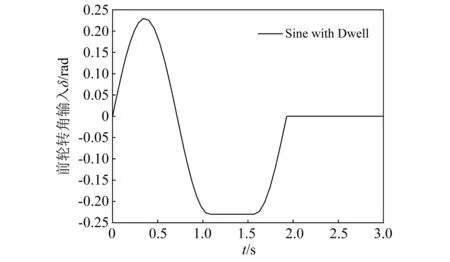
图7 Sine with Dwell 输入的前轮转角Fig.7 Front wheel input of Sine with Dwell

根据式(14)，当τ=1时控制反馈输入受到实际饱和约束，在LMIs中直接忽略包含τ的项，可得到PDC-TS无τ控制的反馈矩阵。传统鲁棒控制模型不考虑轮胎和悬架非线性，根据阈值对状态反馈控制进行饱和处理，不考虑反馈输入的饱和偏差，具体反馈矩阵不再推导。仿真测试结果如图8和图9所示。

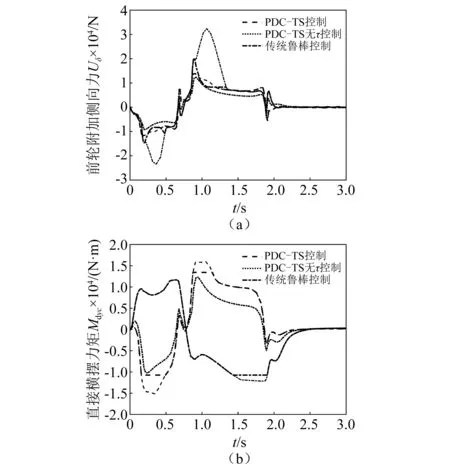
图9 PDC-TS方法的实际输入(粗线)和反馈输入(相同线型细线)Fig.9 Saturation input(thick lines)and feedback input(thin lines in same type)with PDC-TS

根据图8，无控制车辆转向过程的运动状态已经到达极限，质心侧偏角、横摆角速度和车身侧倾角已经发散，必须依靠额外输入控制。对比本文PDC-TS方法和传统鲁棒控制，在极限方向盘扰动下，车辆横摆侧倾状态均能保持稳定。根据分布控制架构，PDC-TS在各个子系统下线下求解反馈增益矩阵，满足控制约束和性能约束，最后得到非线性鲁棒控制的反馈增益矩阵，在极限状态下始终使系统保持较好的稳定性能。

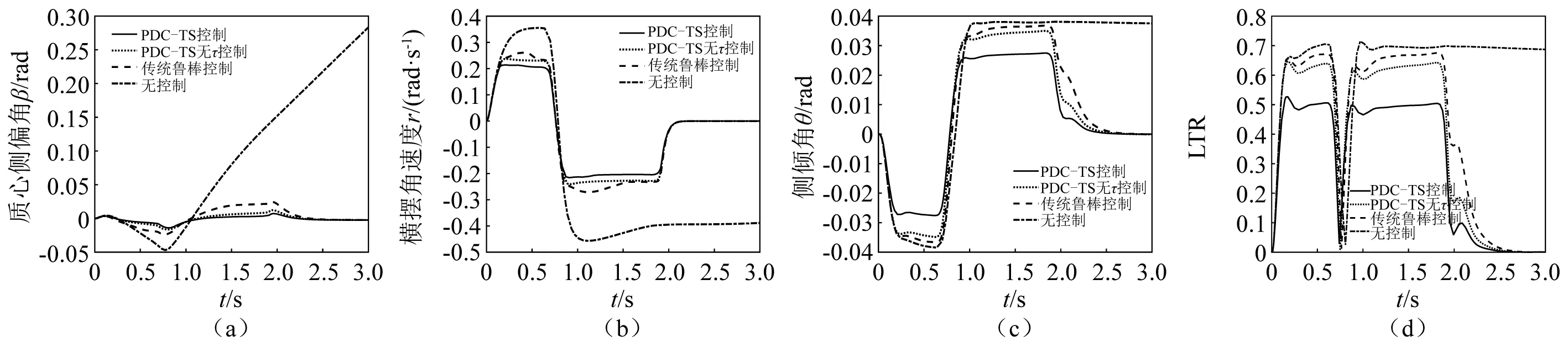
图8 PDC-TS方法横摆侧倾仿真结果Fig.8 Simulation result of yaw-roll with PDC-TS

从图8(a)、图8(b)和图8(c)可以看出，本文方法下质心侧偏角、横摆角速度和车身侧倾角更稳定、幅值更小，收敛速度更快，尤其在转向极限的差异更加明显。结合图4期望横摆运动的比较，通过实时更新线性子系统的隶属度h，本文PDC-TS方法能够更准确地逼近系统非线性。此外，由于对侧倾性能指标的约束，本文PDC-TS方法下的横向载荷转移率LTR处于较小范围内，如图8(d)所示，说明本文方法能有效控制车辆横摆侧倾的综合稳定性能。

图9对比了极限转向过程的控制输入，结合图5动态阈值的比较，由于传统鲁棒控制方法忽略轮胎非线性对预期转角增量的影响，导致主动前轮转向的附加侧向力反馈输入较大，产生较大的预期横摆力矩。从而影响直接横摆力矩反向补偿，导致主动转向和直接横摆力矩控制效果抵消，降低极限状态下控制输入的准确性和有效性。本文PDC-TS方法通过对车辆非线性的准确描述，以及前轮附加侧向力动态阈值对子系统反馈控制的约束，改善了前轮附加侧向力输入。当轮胎进入非线性过程，由于动态阈值的约束，前轮附加侧向力减小，控制不足部分由直接横摆力矩补偿，提高极限状态系统控制的准确性。

此外结合图8和图9，对比PDC-TS松弛因子τ=1和0<τ<1对控制结果的影响，可以看出，τ=1相当于对反馈输入施加硬约束，使反馈输入始终不超出饱和约束，以牺牲横摆侧倾稳定性作为代价。本文控制根据松弛因子0<τ<1，允许反馈输入在一定范围内超出限制，提高执行器利用率，并将饱和偏差作为有界扰动进行控制，显著改善极限状态下车辆的横摆侧倾稳定性。

4 硬件在环试验

为进一步验证本文控制输入的有效性，基于Trucksim-Labview软件建立被控车辆模型，结合NI-PXI实时交互上位机和下位控制器及台架信号，对PDC-TS控制器进行硬件在环仿真测试。下位控制器PDC-TS接收上位机中车辆模型运行状态，求解得到所需的前轮转角和轮胎制动力。

根据转向系统方向盘传动比及制动系统压力传递函数，硬件在环试验台架将下位控制器输入转换为方向盘转角和轮缸制动压力。由于转向系统和制动系统实际存在动态执行过程，试验台架中的执行控制器采用常见的PID算法跟踪，该部分非本文研究内容，故不再赘述。硬件在环试验流程如图10所示，方向盘转角和轮缸制动压力信号分别由转角传感和压力传感器获取。

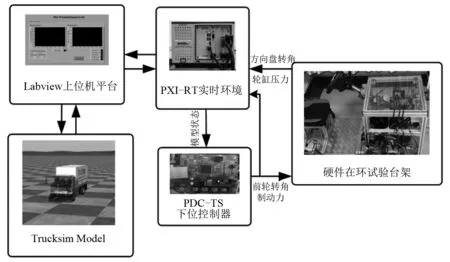
图10 Trucksim-Labview 硬件在环测试流程Fig.10 Trucksim-Labview hardware in loop

结合T-S车辆模型式(10)和动态模糊观测器，AFS+DYC的前轮转角增量和轮胎制动力可表示为

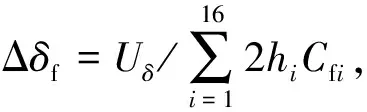
(34)

式中，Fbl和Fbr分别为后轴左、右轮制动力，根据的Mdyc正负号选择制动侧。

硬件在环试验结果如图11所示，传感器采集信号转化后与期望值进行对比。试验过程存在动态特性和观测噪音，除去试验结果的延迟和抖动，主动前轮转角增量输入、左后轮制动力和右后轮制动力的试验结果与期望值基本一致。硬件在环试验结果表明，非线性模糊分布控制PDC-TS下AFS+DYC的集成控制输入是可行的。

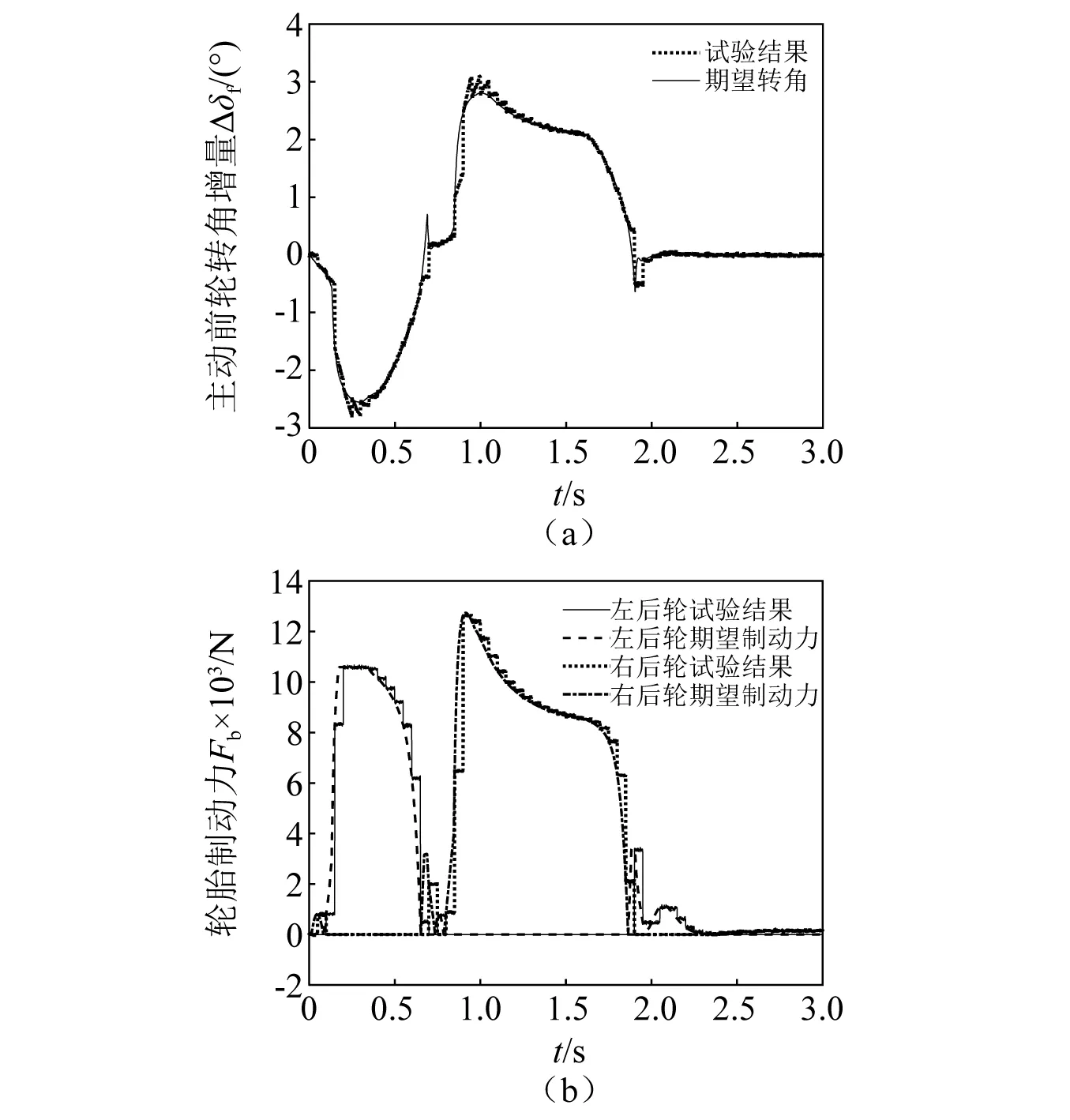
图11 硬件在环试验结果Fig.11 Results of hardware in loop

5 结 论

针对极限状态下车辆转向非线性和执行器饱和问题，本文研究总结如下：

(1)采用Takagi-Sugeon方法建立车辆3自由度横摆侧倾模型，结合模糊观测器实时获取模型动态参数。为准确反映车辆转向稳态过程，在T-S框架下建立改进横摆参考模型，相对于传统横摆参考模型更加准确。

(2)引入松弛因子提高执行器利用率，将反馈输入的饱和影响作为有界扰动进行控制。构建T-S框架下主动前轮输入的动态饱和阈值，能够改善主动转向AFS和直接横摆力矩DYC协调输出。

(3)基于分布控制方法设计状态反馈模糊分布控制器PDC-TS，并将车辆横摆-侧倾H∞性能控制转换为线性矩阵不等式LMIs凸优化问题，最后联合Trucksim-MATLAB/Labview软件进行控制仿真和硬件在环试验验证。结果表明，对于强非线性的车辆横摆侧倾过程，通过实时更新线性子系统隶属度，使本文方法控制更加简洁准确，引入松弛因子充分地利用了执行器工作范围，并在输入饱和约束下保持控制稳定性。