地铁致凸形地貌地表振动局部放大现象实测及机理分析

赵江涛， 牛晓凯， 苏 洁， 王宇哲

(1. 北京市市政工程研究院，北京 100037； 2. 北京交通大学 隧道与地下工程教育部工程研究中心，北京 100044)

近年来，随着我国城市现代化进程的不断发展，以地铁为主的城市轨道交通得到了迅猛发展，并逐渐深入到居民区、文教区、商业区等[1]。然而，地铁在给城市居民出行带来极大便利的同时，随之产生的环境振动污染问题也日益严重，相关投诉也日益增多。研究地铁运行引起的地表振动衰减规律，是周边环境振动评价和隔振、减振设计的基础，其一般规律[2]为：由于地层几何阻尼和材料阻尼的共同作用，地铁运行引起的地表振动总是随着振中距(即振源在地表投影与地表点之间的距离)的增大而单调衰减。真实环境中由于振源特性差异、成层土的不均质性、地形地貌的限制等原因，导致地铁运行引起的地表振动随着振中距的增大而出现局部反弹放大的现象，我们称之为地表振动“局部放大”或存在地表振动“局部放大区”。

目前对于地铁运行引起的地面振动局部放大现象的研究较少。马蒙[3]采用落锤激振试验对地表振源和埋置振源在均匀半空间、成层半空间下的地表振动放大区进行了研究。张啟乐等[4]采用数值计算方法验证了地铁运行情况下地表振动放大区的存在，并认为振动放大区第一次出现在距离隧道约20～30 m的位置。宗刚等[5]通过对上海3处典型的埋置地铁行经场地的地表振动测试，研究认为地表振动的衰减曲线均存在局部放大区，第一局部放大区(主放大区)最为显著，位于1倍埋深的振中距(地表与振源投影点距离)附近。上述研究主要针对地面或地下振源情形下平整地形局部放大现象进行研究，尚未见到针对地铁(地下埋置振源)运行引起的凸形地貌地表振动局部放大区的相关研究。

凸形地貌(即广义的边坡或台阶)主要指突然相对高于邻区或新构造上升形成的地貌。相对于平整地形，凸形地貌会因改变近场入射波的传播路径并存在明显坡面效应而具有其独特的振动特性。目前轨道交通运行对凸形地貌的影响主要集中在铁路行业。卢华喜等[6]曾研究凸起地形宽度、形状、高宽比以及地基土性质对地面铁路环境振动的影响规律；张光明[7]也曾对高速铁路路堤(凸起)段和路堑(凹陷)段地表振动响应特点进行研究。在对法源寺文保区进行大范围地表振动测试的过程中，发现浏阳会馆位置为典型的凸形地貌，测试结果表明该位置存在明显的振动放大现象，因此，本文基于现场实测及相关理论研究首次对地铁致凸形地貌地表振动局部放大现象进行特征及机理分析。

1 法源寺文保区现场测试

法源寺历史文化街区是北京市第二批历史文化保护区之一，也是目前北京旧城内唯一未经开发的文保区。该区域居民长期受到既有地铁4号线的振动影响。既有地铁4号线菜市口-陶然亭站区间位于文保区东侧，南北向布设，该区间采用矿山法施工，其中K6+000～K6+271.7左右线均为马蹄形标准断面，中心间距15 m；K6+271.7～K6+380左线为马蹄形标准断面，右线为停车线扩大断面。

工程平面图见图1，地铁里程K6+270、K6+343位置剖面图见图2、图3。

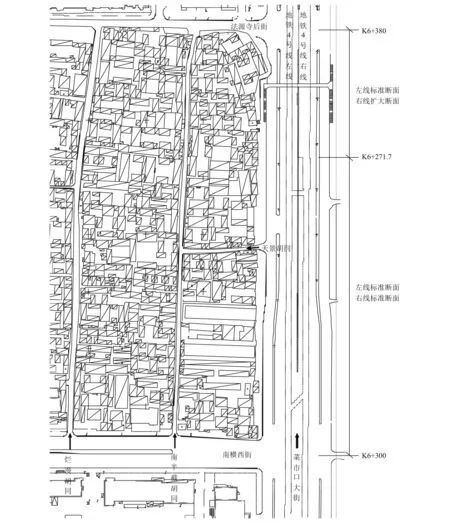
图1 法源寺地区工程平面图Fig.1 Engineering plan of Fayuan Temple

图2 K6+270断面剖面图(m)Fig.2 Sectional drawing of K6+270 (m)

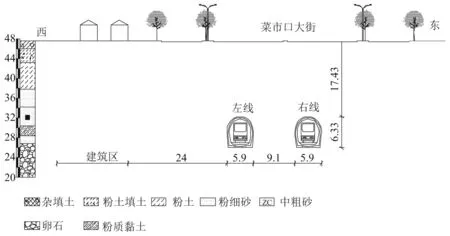
图3 K6+343断面剖面图(m)Fig.3 Sectional drawing of K6+343(m)

由于地铁运行引起周边地表的水平振动一般小于其垂向振动10 dB，在评价环境振动影响时，可以垂向振动为主[8]，因此本次主要对区域内的地表进行铅垂向振动测试。本次采用TCD-16D动态信号测试分析系统+V001型磁电式加速度传感器对该区域进行振动测试，传感器量程±20 m/s2，灵敏度为0.298 V/(m/s2)，频带0.25～200 Hz。为剔除菜市口大街地面交通振动影响，测试时间选择早6点左右，本文相关测试数据均为地铁左线运行引起。测试方法参照规范[9]执行。现场振动测试照片见图4。

图4 现场仪器布置Fig.4 Layout of the field instruments

本次对文保区54 000 m2的区域进行了地表振动测试，限于篇幅，本文只对存在地表振动局部放大的区域进行论述，现场测点布置图见图5。

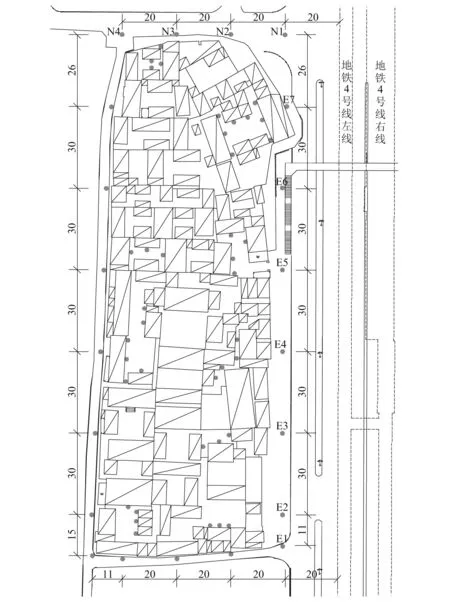
图5 现场测点布置Fig.5 Layout of monitoring points

2 振动放大区位置分析

本部分采用中国国标GB 10070-88《城市区域环境振动标准》[10]中Z振级VLz作为评价指标，对该地区的区域振动特征进行分析，等值线图见图6。

图6 Z振级等值线图Fig.6 Isogram of Z direction vibration degree

由图6可知，距离天景胡同0～130 m的区域，地表振动随着振中距的增大而单调衰减，符合地铁运行引起地表振动的一般规律；但距离天景胡同130～170 m的区域，地表振动随着振中距的增大而先增大后减小，在浏阳会馆位置出现了局部振动反弹增大现象，即出现地表振动“局部放大区”。浏阳会馆位置为典型的凸形地貌，详见图7，凸型地貌地表高出菜市口大街1.2～1.8 m，边缘设重力式挡墙，垂直边坡。

图7 凸形地貌现场照Fig.7 Pictures of the protruding topography

为进一步确定振动放大区的位置，在浏阳会馆位置的凸形地貌上垂直地铁加密布置地表测点，具体测试结果见图8。

图8 浏阳会馆及法源寺后街地表竖向加速度峰值曲线Fig.8 Acceleration amplitude of ground vibration in Liuyang Guild Hall and Fayuan Temple Back Street

由图8可知，浏阳会馆凸形地貌位置地表竖向加速度峰值大于法源寺后街平整地形位置，并在距离地铁左线中线25～50 m位置存在振动放大现象，为典型的地表振动“局部放大区”。由于相关测试数据采集时该位置为地铁左线在运行，故按单线隧道考虑，地表振动“局部放大区”位置约为1.5～3.0倍左线隧道埋设。

3 凸形地貌地表振动放大区形成机理分析

对于平整地形，马蒙、宗刚等曾对地下振源引起的地表振动放大区形成机理进行过较为深入的研究，其研究认为地表振动主放大区主要位于振中距1～1.5倍隧道埋深位置附近，形成机理主要为：地表各点的入射体波传递行程不同，从而导致其衰减程度存在差异，加之各近场体波与面波等的叠加效应，最终导致平整地形地表振动局部放大区的出现。然而，浏阳会馆振动放大区的位置与上述结果并不相同，可见凸形地貌的存在不仅改变了原地表附近体波和面波的叠加结果，还会对传递到凸形地貌内的波起到放大作用。

3.1 凸形地貌振动传播路径分析

对于地下埋置振源，当地铁直线行驶时，列车振动主要以P波形式传播[11]，当某一P波非垂直入射到两地层分界面时，不仅会产生反射P波和折射P波，还会发生切变产生反射SV波和折射SV波，此时反射波向地层深度继续传播，折射波继续向上传播。此时假定凸起地貌为单一均质地层，则入射到凸起地貌内的体波，一方面会在坡脚除产生绕射，根据惠更斯原理，将坡脚看作新的振源点，则一部分振动波会继续向凸起地貌地表传播，另一部分会转化为面波沿坡面传播；另一方面原远离坡脚的入射体波会直接传递到地表，这样界面透射波、坡脚绕射波、地表面波及地层1中的多次反射波便会在地表进行叠加，见图9。某一时间，当凸起地貌某点的各种波形相位相同时，并会出现振动幅值增大、振动增强的情况。

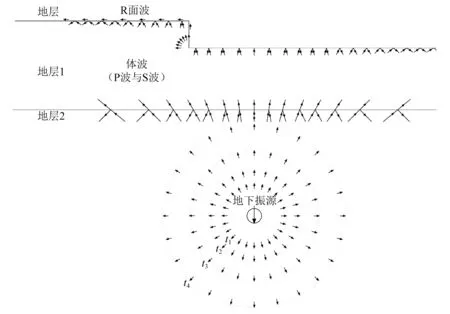
图9 地下振源在凸起地貌中的振动传播路径示意图Fig.9 Diagrammatic sketch of propagation path in the protruding topography induced by subway traffic vibration

3.2 凸形地貌振动放大机理分析

实际的凸起地貌一般并非单一均质地层，而是可以将该凸形地貌高度看作是若干介质层的组合[12]，那么地层波阻抗就会对波形的传递起到至关重要的作用。

当平面简谐P波在界面正入射不产生切变时，则入射P波从介质1入射到两介质的界面时，则只会产生反射P波和进入介质2的折射P波，根据波阵面上的动量守恒可知

(1)

σr+σf=σz

(2)

υr+υf=υz

(3)

式中：σr，σf,σz为质点的入射、反射和折射应力；υr,υf,υzσz为质点的入射、反射和折射速度;ρ1,C1为介质1的密度和P波波速;ρ2,C2为介质1的密度和P波波速。

质点在介质中传播时，存在下述关系

σ=ρCυ

(4)

联立式(1)～式(4)，可得

(5)

(6)

(7)

(8)

由式(5)～式(8)可知：当ρ1C1>ρ2C2时，则有σf<0，υf>0，υf>υr，表明质点的运动方向与入射波相同，P波从介质1进入介质2振动加强。

如前所述，若将凸形地貌看作是若干介质层的组合，当地下振源产生的入射波在凸型地貌中由下向上传递过程中，由于地层波阻抗随地层深度的减小而减小，折射波引起的质点振动速度会大于入射波，因此，波每传递到一层波阻抗较小的介质中，波速便会被放大一次，最终由于凸形地貌中界面群折射波的不断叠加，最终导致凸形地貌地表振动的局部放大。

4 地铁致凸形地貌地表振动局部放大数值验证

4.1 二维计算模型的建立

采用有限元软件进行相应二维数值计算。根据文献[13]中网格尺寸划分及模型范围确定方法，其中隧道结构、凸形地貌及地层单元网格尺寸分别为0.15 m,0.3 m,0.5～2 m，模型土域尺寸为180 m×60 m，凸形地貌标准高度为1.8 m。

模型边界采用二维黏弹性人工边界，边界单元等效刚度参数为

(9)

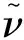
边界等效单元阻尼系数为

(10)

式中：ρ为介质质量密度；cS为土体内S波波速；cP为土体内P波波速。

地铁运行产生的激振力采用实测荷载数定法获得。首先在列车停运时测定某点激励力下钢轨下部竖向加速度响应，确定传递函数；然后测定出列车运行时钢轨下部竖向振动加速度，并根据传递函数推导出复频域的列车动载荷；最后根据地面振动加速度响应对上述动荷载进行修正。现场测定照片详见图10。确定列车动荷载后换算为扣件支反力，计算结果详见图11。

图10 地铁振动荷载现场测试Fig.10 Field test of subway train’ vibration load

图11 扣件支反力时程图Fig.11 The time-history curve of rail fasteners’ counter-force

数值计算过程中，采用传统的Rayleigh阻尼理论计算阻尼矩阵，其中阻尼比取为0.05。动力计算过程中计算时步为0.001 s，截止频率为200 Hz。

模型内地层动力学参数详见表1，衬砌材料参数见表2。二维数值计算模型如图12。

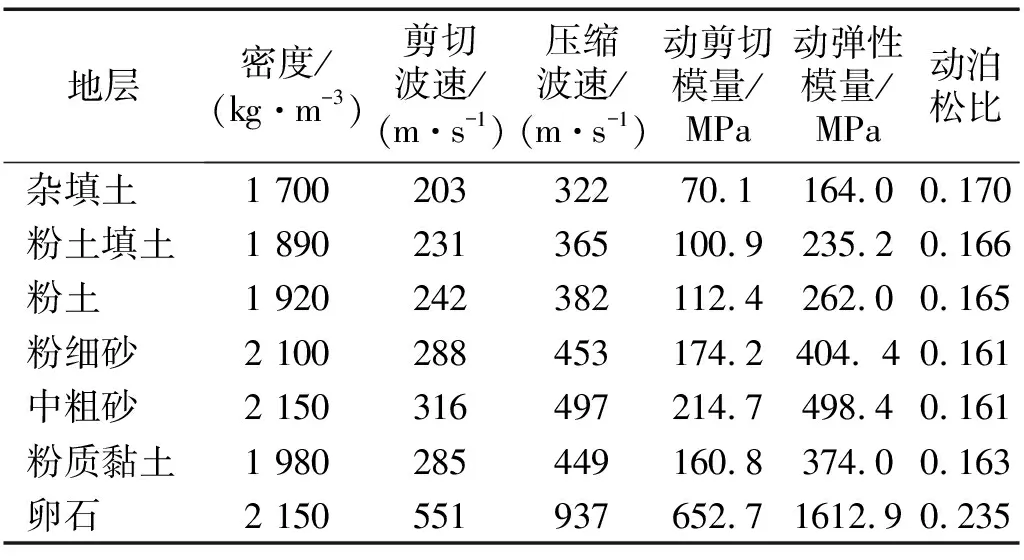
表1 地层动力计算参数Tab.1 Stratum parameters of dynamic analysis

表2 衬砌材料参数Tab.2 Parameters of lining materials

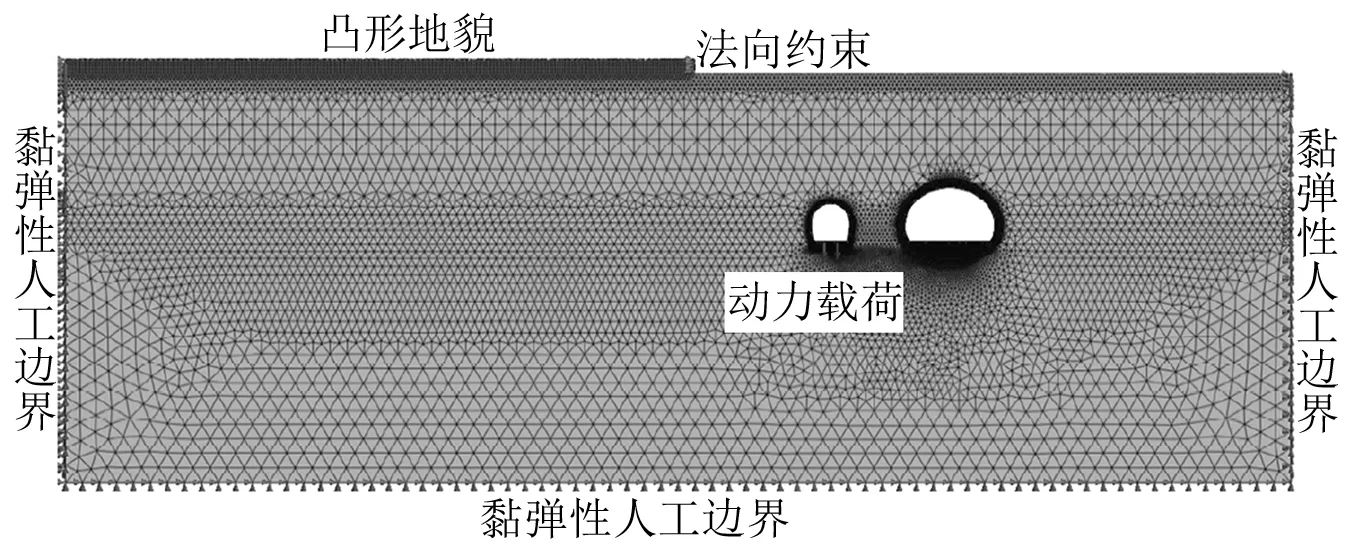
图12 二维有限元模型Fig.12 Two-dimensional finite element model

4.2 计算模型的验证

为了验证二维计算模型的准确性，建立平整地形数值计算模型，利用法源寺后街测点(测点编号为N1、N2、N3、N4)现场实测结果进行比对，图13为现场实测与数值计算结果对比曲线，由图13可知仿真的地表振动加速度峰值与现场实测结果的衰减趋势一致，各测点数值计算结果与实测值基本一致。表明本文建立的二维数值计算模型与实际结果的吻合度较高。

图13 地表竖向加速度峰值曲线Fig.13 Acceleration amplitude of ground vibration

4.3 凸起地貌参数分析

利用二维数值计算模型，针对浏阳会馆凸形地貌进行列车振动影响数值计算。具体工况设置如表3。

表3 计算工况Tab.3 Calculation conditions

由图14可知:

(1)距地貌边缘0～3 m(即距隧道中心17～20 m)数值计算结果与实测值偏差均较大，主要是因为地貌边缘只设置了法向约束边界，而真实地貌边缘为重力式挡墙，两者对地层的约束效应及边缘附近地层参数均相差较大。

(2)距隧道中心20 m以外，地表竖向加速度峰值基本呈现先减后增，最后逐渐减小并逐渐收敛的形状，地表振动存在明显的局部放大现象。

(3)凸形地貌地表振动局部放大效应：工况1>工况2>工况3，表明地层波阻抗由深及表逐渐衰减时，凸形地貌的振动放大效应最为明显，进一步验证了4.2节凸形地貌振动放大机理的准确性。

(4)工况1中凸形地貌地层波阻抗由深及表逐渐衰减，其计算结果与实测值吻合度最高，地表振动放大区的位置主要分布在距离左线隧道中心25～50 m位置，与Z振级等值线图中结果基本吻合。

完成工况4相关计算后，提取凸形地貌距离地貌边缘3 m以外区域地表竖向加速度峰值，详见图15。由图15可知，凸形地貌地表竖向加速度峰值随着地貌高度的增大而增加，达到临界值后，又会随着地貌高度的增大而降低，表明凸形地貌对其地表振动加速度具有一定的振动放大效应，但放大效应并不是无限的。

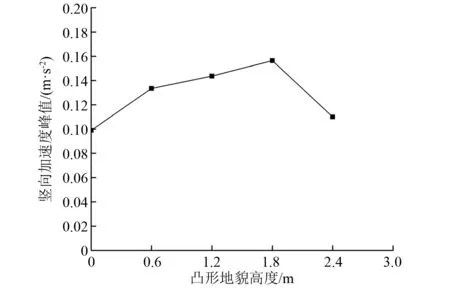
图15 工况4数值计算结果Fig.15 Numerical results of the fourth condition

5 结 论

本文首先完成了地铁运行影响下法源寺文保区的现场振动测试，发现浏阳会馆位置存在明显的地表振动局部放大现象，通过相关分析得出如下结论：

(1)浏阳会馆位置为典型的凸形地貌，其地表振动“局部放大区”出现在振中距1.5～3.0倍左线隧道埋设范围内，这与平整地形主振动放大区的位置(约1～1.5倍隧道埋深)并不相同，表明凸形地貌不仅会改变原地表附近体波和面波的叠加结果，还会对传递到凸形地貌内的波起到放大作用。

(2)基于弹性波场理论，分析了地下埋置振源下凸形地貌地表振动放大区形成机理为：传递到凸形地貌内的振动波一方面会在坡脚产生绕射，形成以坡脚为新的振源点的波场，并部分转化为面波沿坡面传播，这样远离坡脚的界面透射波、坡脚新绕射波、坡面面波及表层土内的多次反射波便会在凸形地貌地表进行叠加；另一方面凸形地貌为若干介质层的组合，其波阻抗一般会随地层深度的减小而减小，传递到凸形地貌的透射波在向上传递的过程中，波速会不断放大，最终导致凸形地貌地表振动的局部放大。

(3)采用二维有限元模型对地铁致凸形地貌地表振动局部放大现象进行了数值验证，结果发现凸形地貌地表竖向加速度峰值在其波阻抗由深及表逐渐衰减时，凸形地貌地表振动局部放大效应最为明显，数值计算结果与实测值基本吻合。研究结果还发现凸形地貌地表竖向加速度峰值随着地貌高度的增大而增加，达到临界值后，又会随着地貌高度的增大而降低，表明凸形地貌的振动放大效应并非会随着高度增加的而无限增大，其只在一定高度范围内存在。