基于欧进萍谱的广义Maxwell耗能结构随机响应简明解法
刘美华, 邹万杰, 葛新广, 李创第
(广西科技大学 土木建筑工程学院, 广西 柳州 545006)
结构控制能迅速地衰减结构的振动反应[1-2],在抵御强地震或风荷载时,安装耗能装置能有效减小主体结构的破坏[3-5]。线性黏弹性阻尼器利用黏弹性材料来吸收振动能量,为更精确地描述黏弹性阻尼器的本构关系,国内外学者提出了各种力学模型,比如Maxwell模型[6-7]、Kelvin模型[8]、一般积分模型[9-10]、广义Maxwell模型[11-12]等。其中Maxwell模型和Kelvin模型是形式单一的力学模型,表现出的是单一的松弛行为、单一松弛时间的响应。而实际工程中,主体结构是多层次性的,并且运动单元也具有多重性,对应于结构中不同的单元,都应有不同的松弛时间。因此,为了反映黏弹性阻尼耗能结构的响应特性,采用多元件组合的广义Maxwell力学模型来分析结构动力响应,更具有合理性。
地震发生在时间、空间、强度方面都具有明显的随机性[13],最早用于模拟随机地震地面运动的模型是白噪声模型,接下来Kanai[14]又提出用平稳过滤白噪声模型来模拟地震地面运动过程,即金井清模型,这一模型在地震工程界得到了广泛应用[15-17]。该模型将地表覆盖土层视为线性单自由度滤波器,但假定基岩地震动为理想白噪声,因此,并不能反映基岩的动力特性,也无法求出地面位移、速度、加速度导数方差的有限值,据此,欧进萍院士[18]提出了平稳过滤有色噪声谱模型,即欧进萍谱,其继承了金井清谱的优点,具有明确的物理意义,同时假定基岩运动为马尔柯夫有色频谱,更能反映基岩的动力特性,也能够求得地面位移、速度以及加速度过程导数方差的有限值,因而更方便结构随机地震响应分析。
用于黏弹性耗能结构的响应分析方法有扩阶复模态法[19-20]、虚拟激励法[21-22]、模态应变能法[23]、强行解耦法[24]等。模态应变能法采用小阻尼假设,当阻尼较大时误差也较大。强行解耦法由于忽略对角线元素,当阻尼较高时,也会引起较大误差。虚拟激励法求解谱矩和方差需要借助数值积分,其计算精度受积分区间和积分步长的影响,而且,当有多个平稳随机激励且互相具有相干性时,其计算量浩大。扩阶复模态法是通过建立状态方程来求解,当阻尼力表达式已知时,是一种精确的求解方法,但是,因扩阶变量个数增多,导致计算效率较低。为此,本文兼顾计算精度和效率,提出了一种扩阶之后简明的结构响应解析分析方法,即将结构运动方程、阻尼器本构方程和滤波方程联立为状态方程,再运用复模态法解耦该联立方程,得到由白噪声激励表示的结构响应统一表达式,最后由平稳随机过程谱矩的定义,得到阻尼器及结构系列响应(含结构位移及结构速度、层间位移及层间速度、阻尼器受力及其变化率)0~2阶谱矩的解析解。
1 结构运动方程
1.1 原结构运动方程
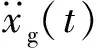
图1 结构计算简图Fig.1 Calculation diagram of the structure
结构运动方程为
(1)
其中,
I=[1, 1, …, 1]T,
x=[x1,x2, …,xn]T,
PQ(t)=[PQ1(t),PQ2(t),…,PQn(t)]T
1.2 广义Maxwell阻尼器本构关系
广义Maxwell模型阻尼器是由一个线性弹簧和一系列Maxwell模型单元并联而成,广义Maxwell模型阻尼器计算简图如图2所示,Maxwell模型阻尼器计算简图如图3所示。
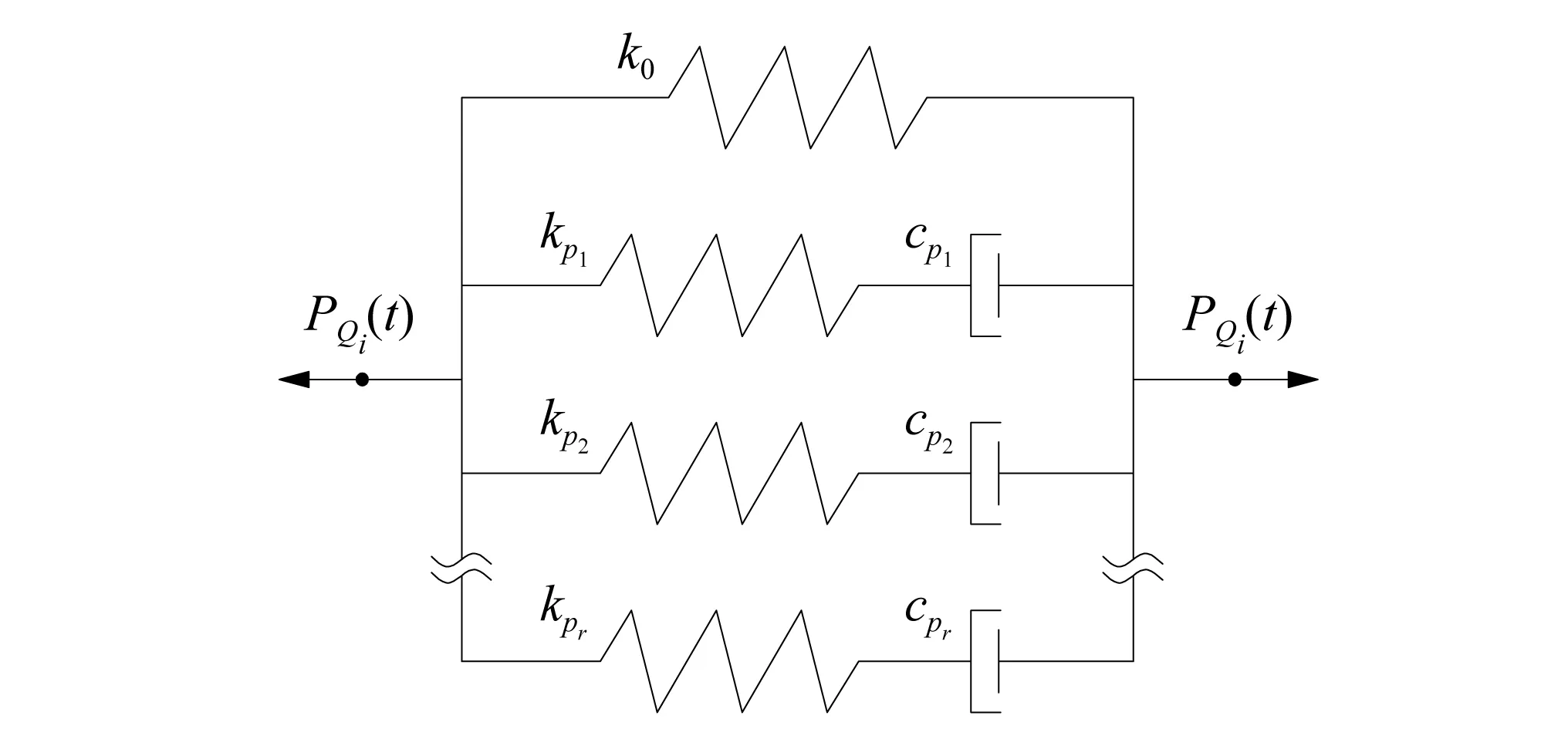
图2 广义Maxwell模型阻尼器Fig.2 Generalized Maxwell model damper
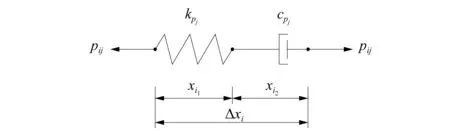
图3 Maxwell模型阻尼器Fig.3 Maxwell model damper
广义Maxwell阻尼器本构关系为
(2)
式中:PQi(t)为第i层阻尼器的总阻尼力;k0为阻尼器平衡刚度;pij为每个Maxwell单元的阻尼力。其中:i=1~n,n为楼层数目;j=1~r,r为广义Maxwell阻尼器中标准Maxwell阻尼器单元的个数。
将式(2)写成矩阵形式,有
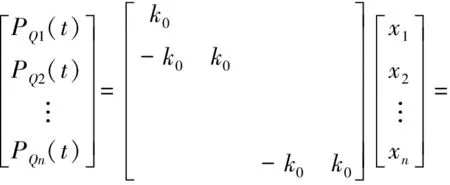
(3)
式中:l为元素均为1的1×r阶向量;pi为r×1阶向量,pi=[pi1,pi2, …,pir]T。
将式(3)简写为
PQ(t)=K1x+D1P
(4)
式中:D1为n×rn阶对角阵,rn指r×n项,D1=diag[l,l, …,l];P为rn×1阶向量,P=[p1,p2, …,pn]T。
各分支Maxwell阻尼器微分关系为
(5)
式中,kpj,cpj分别为第j个标准Maxwell阻尼器单元的刚度和阻尼,j=1~r。
将式(5)写成矩阵形式,有
(6)
式中:A为r×r阶对角阵,A=diag[kp1/cp1,kp2/cp2, …,kpr/cpr];a为r×1阶向量,a=[kp1,kp2, …,kpr]T。
将式(6)简写为
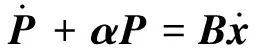
(7)
式中:α为rn×rn阶对角阵,α=diag[A,A, …,A];B为rn×rn阶矩阵。
1.3 重构结构运动方程
欧进萍谱可用滤波方程描述如下
(8a)
(8b)
(8c)
(8d)
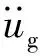
CW(τ)=2πS0δ(τ)
(9)
式中:δ(τ)为Dirac函数。
联立式(1)、式(4)和式(8),重构结构的运动方程
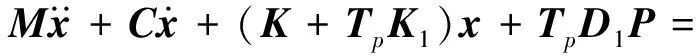
(10)
引入状态变量
(11)
将式(7)、式(8)和式(10)写成状态方程
(12)
其中,
β=[0o10o11o3]T
式中:o1为元素均为0的n×1阶向量;o2为元素均为0的n×n阶矩阵;o3为元素均为0的rn×1阶向量;o4为元素均为0的n×rn阶矩阵;E1为n阶单位矩阵;E2为rn阶单位矩阵。
2 结构响应杜哈梅积分统一表达式
由于式(12)为非经典系统,故用复模态法对其进行解耦。存在右特征向量矩阵U、左特征向量矩阵V和特征值矩阵q使式(12)解耦,特征值矩阵q为对角阵,且满足关系式
(13)
引入复模态变换
y=Uz
(14)
式中,z为广义复模态变量。
式(12)最终可化为如下复模态响应方程:
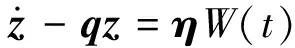
(15)
其中,
(16)
将式(15)写成分量形式,有
(17)
式中:zj,qj和ηj分别为z,q和η的分量;(r+2)n+3为特征向量矩阵的阶数。
式(17)的解为

(18)
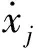
(19)
(20)
式中:uz为右特征向量矩阵U的第z行向量;λz,i为结构动力响应的强度系数,其为λz,i=uz,iηi;j=1~n;z=j+1,n+2+j。
由式(4)、式(11)、式(14)和式(18),第j楼层阻尼力PQj(t)的杜哈梅积分表达式为
(21)
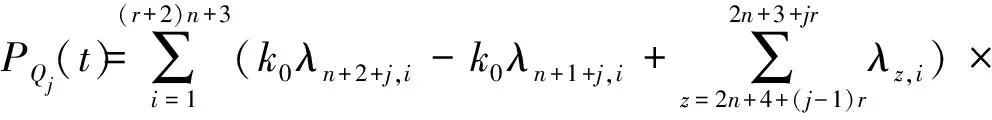
(22)
对式(4)求导,得
(23)
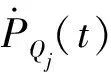
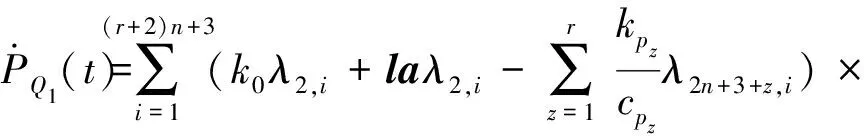
(24a)
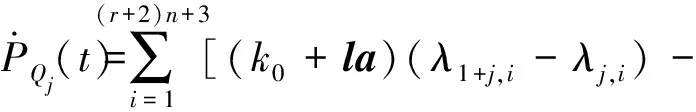
(24b)
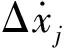
(25a)
Δx1=x1
(25b)
(26a)
(26b)
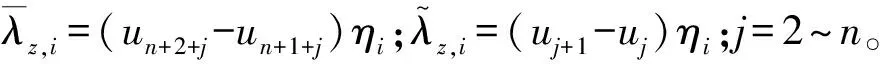
对应于广义Maxwell阻尼器多层耗能减震结构,它们的位移及速度、层间位移及层间速度、阻尼器受力及其变化率响应均具有相似的表达式,所以可将以上参数统一表示为
(27)
Gz,i(t)为结构响应分量,其表达式为

(28)
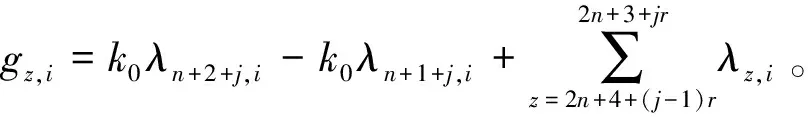
3 结构响应方差与功率谱解析解
由于结构响应分量Gz,i(t)可以作如下相等变换

(29)
则结构响应Gz(t)的平稳协方差函数的表达式为
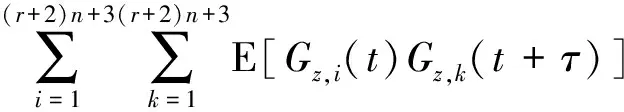
(30)
由式(29)和式(30),得结构响应分量的协方差为
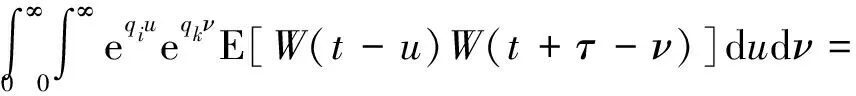
(31)
由于W(t)为具有零均值的平稳白噪声,将式(9)代入式(31),求积可得
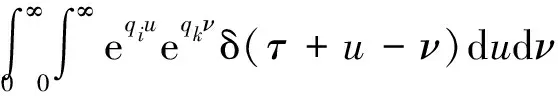
(32)
利用δ(τ)函数的性质,可以将式(32)简化为一重积分
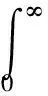
(33)
再对式(33)的积分部分运算,可得
(34)
故由式(30)和式(34),可得在欧进萍谱平稳地震激励下耗能结构响应的协方差为
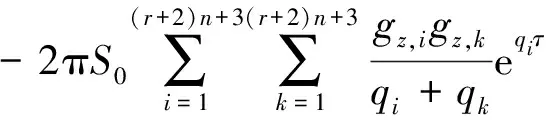
(35)
令
(36)
则结构响应Gz(t)的协方差式(35)可简化为
(37)
在式(37)中,令τ=0,可得结构响应Gz(t)的方差
(38)
由平稳随机过程的功率谱密度函数与协方差函数的Wiener-Khinchin关系[25],结构响应的功率谱可表示为
(39)
将式(37)代入式(39)并对积分部分运算,可得本文方法求得的结构响应功率谱解析解
(40)
由式(20)、式(36)和式(40),得本文方法结构位移x功率谱密度函数
(41)
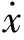
(42)
由式(25)、式(36)和式(40),得本文方法结构层间位移Δx功率谱密度函数
(43)
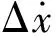
(44)
由式(22)、式(36) 和式(40),得本文方法阻尼力PQ(t)功率谱密度函数
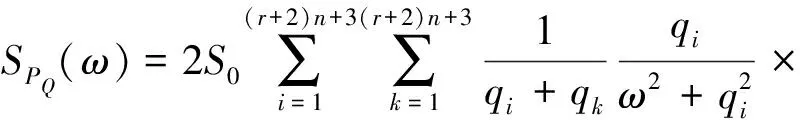
(45)
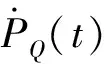
(46)
4 结构响应谱矩解析解
由谱矩的定义,结构响应的j阶谱矩表达式为
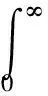
(47)
式(47)中令j=0,得结构位移(绝对位移、层间位移)响应0阶谱矩
(48)
对式(48)积分部分运算可得
(49)
由随机振动理论可知,结构位移响应的0阶谱矩即为随机过程位移方差,式(49)也验证了本文方法的正确性。
结构位移响应2阶谱矩为结构速度响应,可由速度方差表示
(50)
阻尼器阻尼力响应0阶谱矩为
(51)
阻尼器阻尼力响应的2阶谱矩等于阻尼力变化率的方差,即
(52)
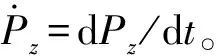
式(47)中令j=1,得结构位移响应1阶谱矩为
(53)
对式(53)积分部分运算可得
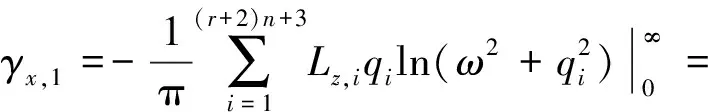
(54)
根据文献[25]可知
(55)
故结构位移响应1阶谱矩γx,1可表示为
(56)
同理,可得阻尼器阻尼力响应1阶谱矩γP,1为
(57)
5 算 例
某十层钢筋混凝土框架结构,第一层至第十层的结构质量为m1~m10=400×103kg,层间刚度为k1~k10=253×106N/m,结构阻尼按Rayleigh阻尼计算,两比例系数分别为a0=0.281 4和a1=0.006 7,结构阻尼比ξ=0.05。每层设置相同的广义Maxwell阻尼器,阻尼器平衡刚度k0=75.90×104N/m,阻尼器两分支Maxwell单元的松弛时间和刚度分别为:μ1=0.08 s,kp1=12.65×105N/m;μ2=0.10 s,kp2=10.63×105N/m。地震烈度为8度,Ⅰ类场地,在欧进萍谱平稳随机地震激励下的各参数取值为:谱强度因子S0=45.24×10-4m2/s3,场地土阻尼比ξg=0.64,卓越频率ωg=25.13 rad/s,基岩的谱参数ωh=8π rad/s。
5.1 功率谱对比
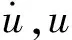
(58)
(59)
式中:u1,un+2分别为右特征向量矩阵U的第1、第n+1行向量。
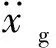
(60)
式中,βi=-(2ξgωgλ1,i+ωg2λn+2,i)。
(61)
欧进萍谱功率谱密度函数的传统表达式为
(62)
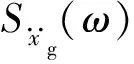
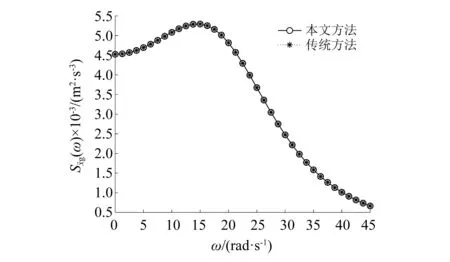
图4 地面加速度功率谱Fig.4 Ground acceleration power spectrum
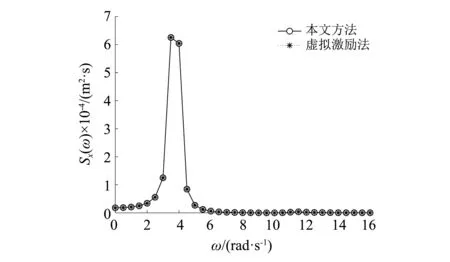
图5 第5层结构位移功率谱Fig.5 Absolute displacement power spectrum of the 5th floor
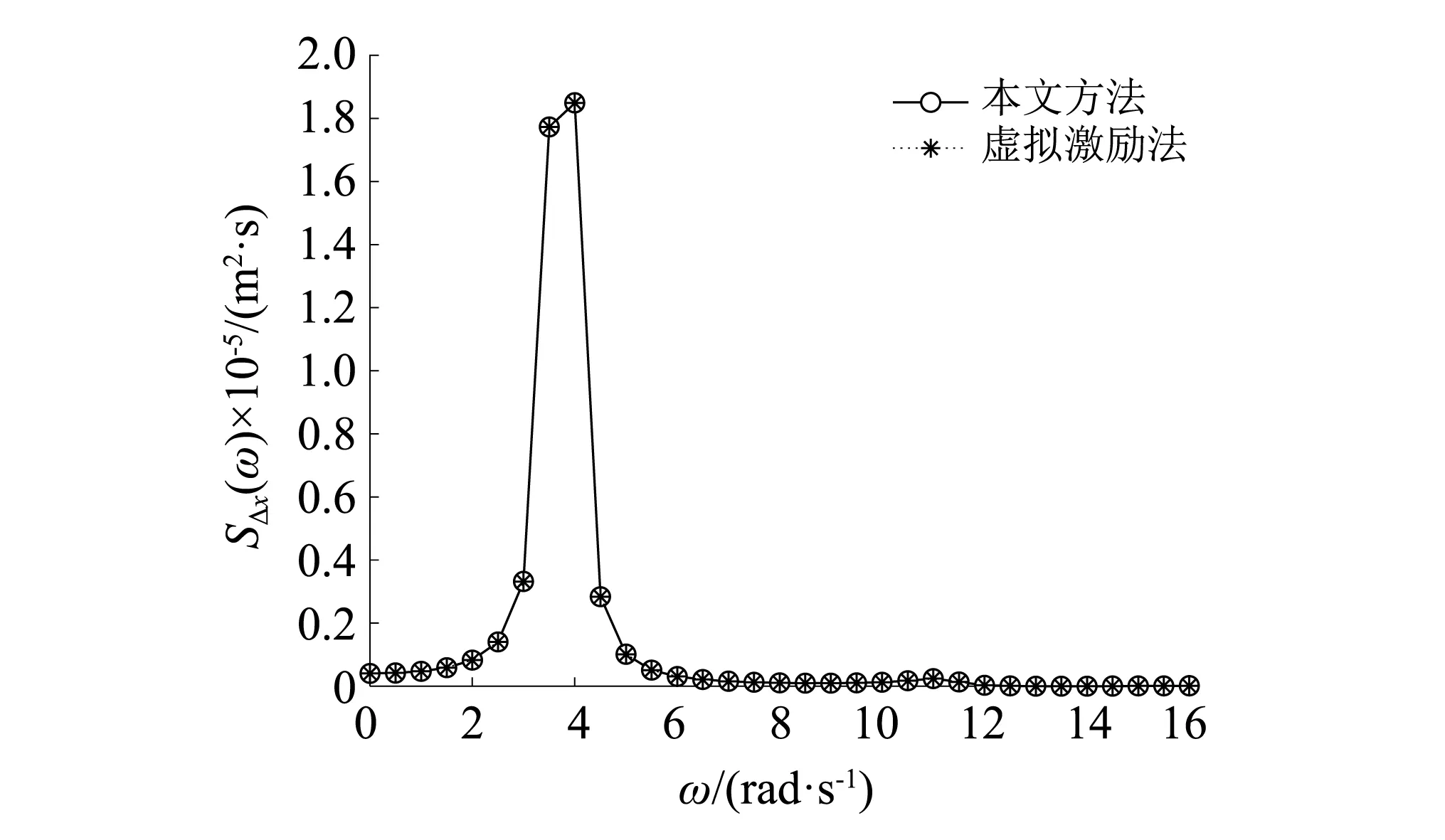
图6 第5层层间位移功率谱Fig.6 Inter-storey displacement power spectrum of the 5th floor
由图4可知,本文激励功率谱图与欧进萍谱传统功率谱图完全吻合,由图5和图6可知,本文方法与虚拟激励法计算得到的结构响应功率谱图形完全吻合,从而验证了本文求得的功率谱密度函数表达式的正确性。而本文将耗能结构在欧进萍谱激励下的结构系列响应功率谱表示为(ω2+qi2)-1的线性组合,表达式更为简洁,更便于后续的积分运算。
5.2 谱矩计算精度和效率对比
为了验证本文谱矩计算方法的正确性和精确性,运用本文方法计算得到的结构响应0~2阶谱矩,与已有虚拟激励法计算得到的谱矩进行对比分析。因为虚拟激励法计算谱矩需要进行数值积分,其计算精度和计算效率与积分区间以及积分步长密切相关,因此,有必要选取不同的积分区间和积分步长进行更全面地对比。为了研究频域积分步长Δω对虚拟激励法谱矩精度的影响,将虚拟激励法积分步长分别取为0.25 rad/s,0.10 rad/s,0.001 rad/s,积分区间统一取为[0,250]。图7~图9为本文方法和虚拟激励法分别取3种不同积分步长计算结构各层位移谱矩γx的对比,图10~图12为本文方法和虚拟激励法分别取3种不同积分步长计算结构各层层间位移谱矩γΔx的对比。
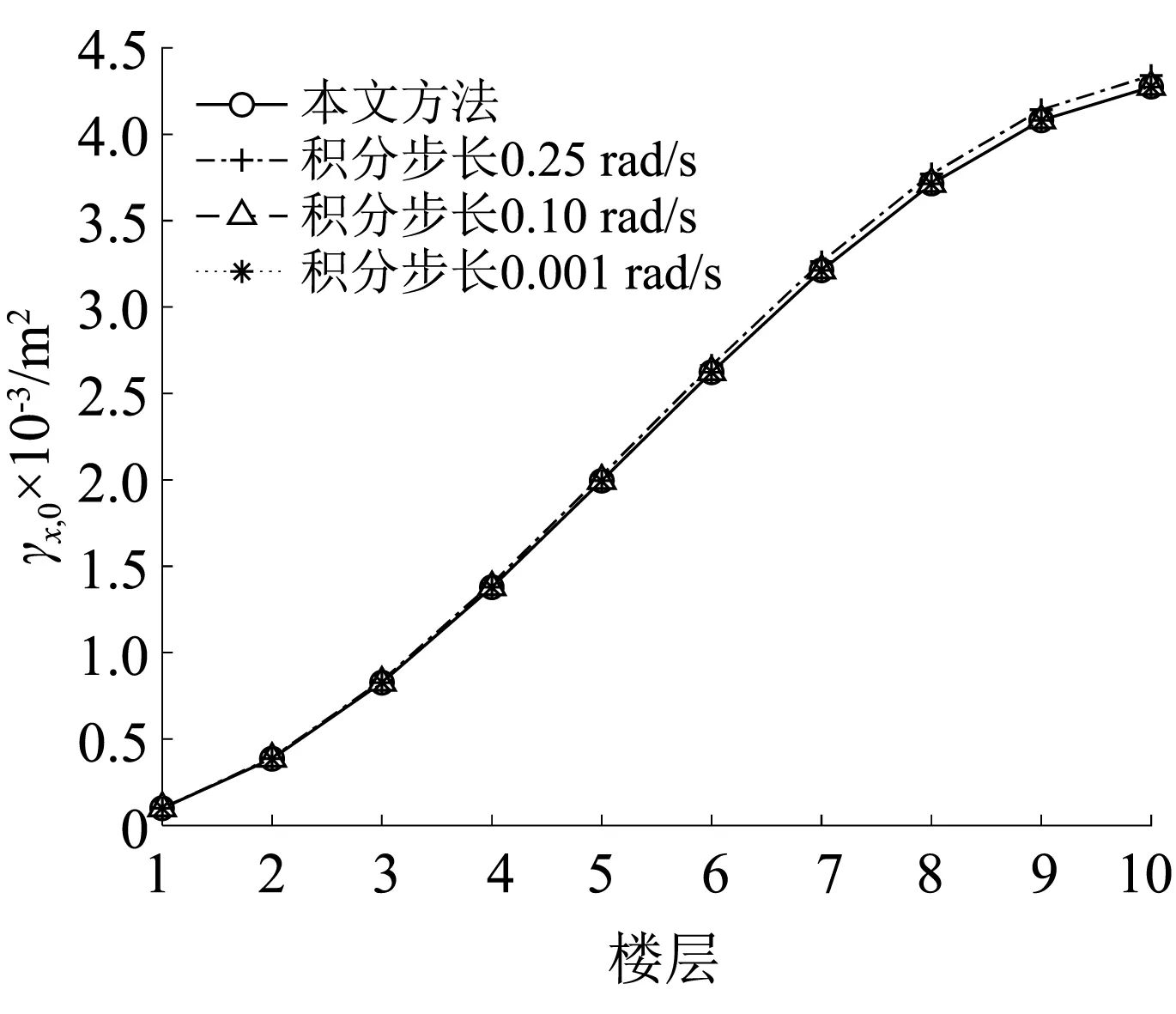
图7 位移0阶谱矩Fig.7 0-order spectral moments ofabsolute displacements
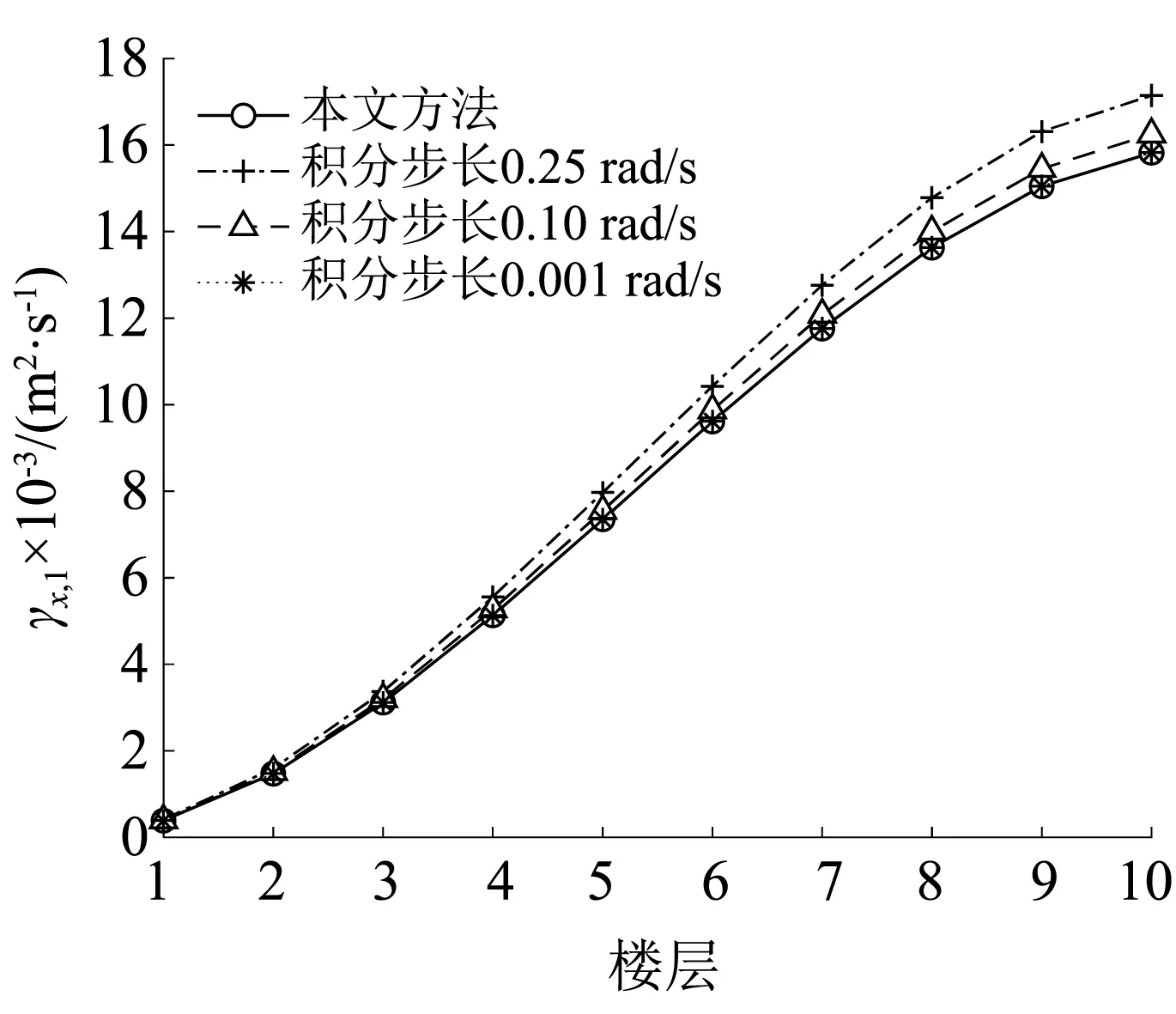
图8 位移1阶谱矩Fig.8 1st-order spectral moments of absolute displacements
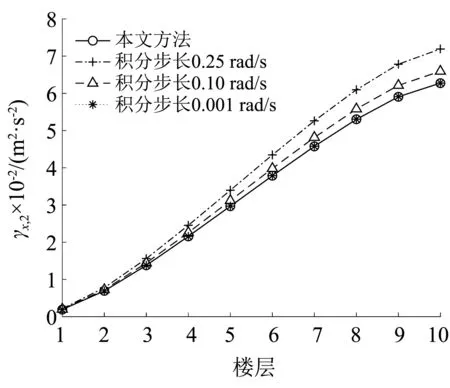
图9 位移2阶谱矩Fig.9 2nd-order spectral moments of absolute displacements
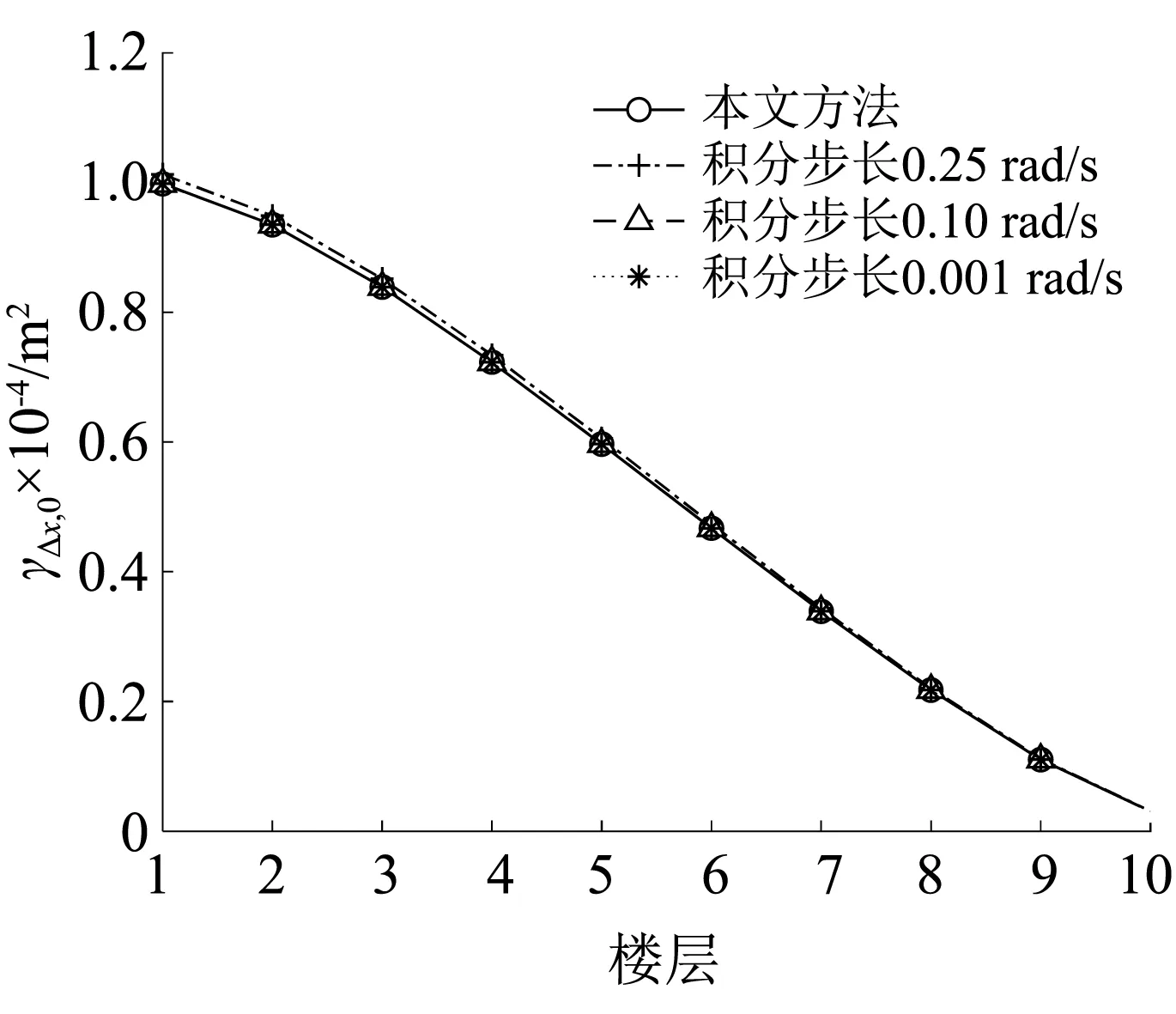
图10 层间位移0阶谱矩Fig.10 0-order spectral moments of inter-storey displacements
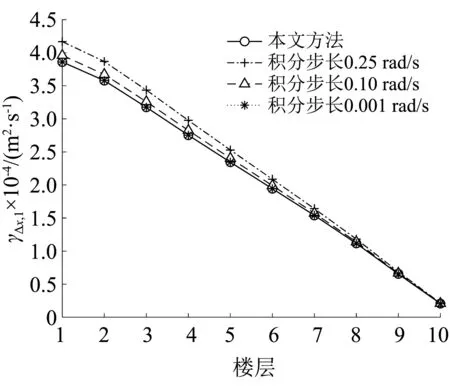
图11 层间位移1阶谱矩Fig.11 1st-order spectral moments of inter-storey displacements

图12 层间位移2阶谱矩Fig.12 2nd-order spectral moments of inter-storey displacements
由图7~图12可知,在积分区间固定的情况下,随着虚拟激励法频域积分步长Δω的减小,虚拟激励法计算得到的结构位移和结构层间位移的0~2阶谱矩值就越逼近本文方法得到的谱矩值,验证了本文谱矩计算方法的正确性和精确性。
为了研究积分区间对虚拟激励法谱矩精度的影响,以计算结构层间位移的0~2阶谱矩为例来进行研究。将虚拟激励法积分区间分别取为[0, 35],[0, 40],[0, 50],积分步长分两种情况取值:①Δω=0.001 rad/s;②Δω=0.000 1 rad/s。图13~图15是第①种情况虚拟激励法分别取3种不同积分区间的谱矩值与本文方法谱矩值之差的绝对值;图16~图18是第②种情况虚拟激励法分别取3种不同积分区间的谱矩值与本文方法谱矩值之差的绝对值,其纵坐标反映的是虚拟激励法谱矩值偏离本文方法谱矩值的大小。
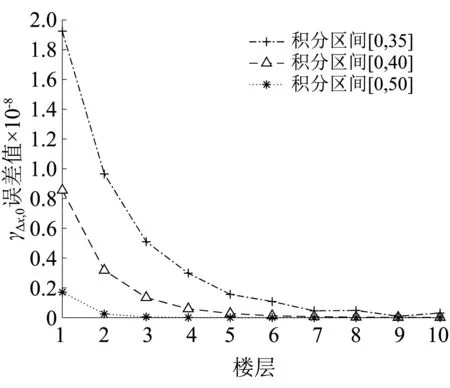
图13 层间位移0阶谱矩误差对比(Δω=0.001 rad/s)Fig.13 Accuracy of 0-order spectral moments(Δω=0.001 rad/s)
虚拟激励法是功率谱分析的精确方法,其功率谱谱矩计算需要进行数值积分,计算精度取决于积分步长和积分区间。当积分上限取值相同时,积分步长取值越小,计算结果精确度越高,第②种情况积分步长是第①种情况积分步长的0.1倍,所以第②种情况谱矩计算精度比第①种情况谱矩计算精度更高。由第①种情况图14和图15可知,部分楼层的层间位移1阶和2阶谱矩值并没有随着积分区间的增大而更逼近本文方法谱矩值,由第②种情况图16~图18可知,结构层间位移0~2阶谱矩值均随着积分区间的增大而更逼近本文方法谱矩值,由此可知,随着频域积分步长Δω的减小和整个积分区间的增大,两种方法计算得到的0~2阶谱矩值误差越小,虚拟激励法得到的谱矩值就更逼近本文方法谱矩值,进一步验证了本文谱矩解为精确解,同时也说明虚拟激励法要想达到更高的精度,须将积分步长取得足够小。
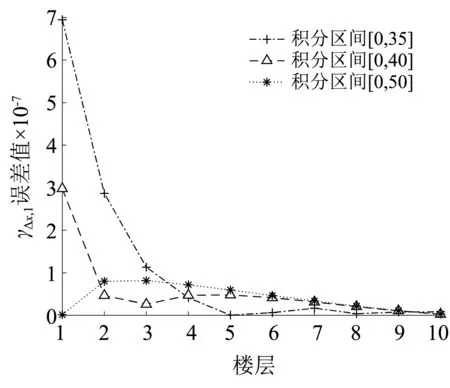
图14 层间位移1阶谱矩误差对比(Δω=0.001 rad/s)Fig.14 Accuracy of 1st-order spectral moments(Δω=0.001 rad/s)
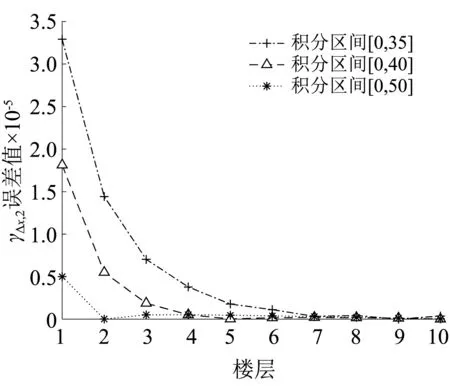
图15 层间位移2阶谱矩误差对比(Δω=0.001 rad/s)Fig.15 Accuracy of 2nd-order spectral moments(Δω=0.001 rad/s)
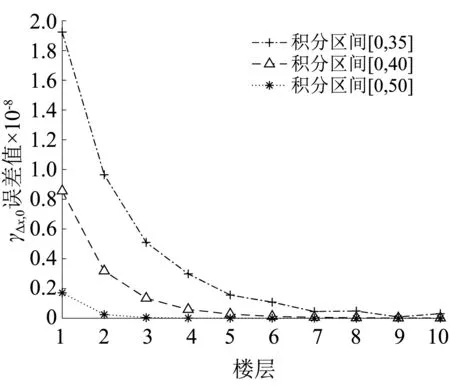
图16 层间位移0阶谱矩误差对比(Δω=0.000 1 rad/s)Fig.16 Accuracy of 0-order spectral moments(Δω=0.000 1 rad/s)
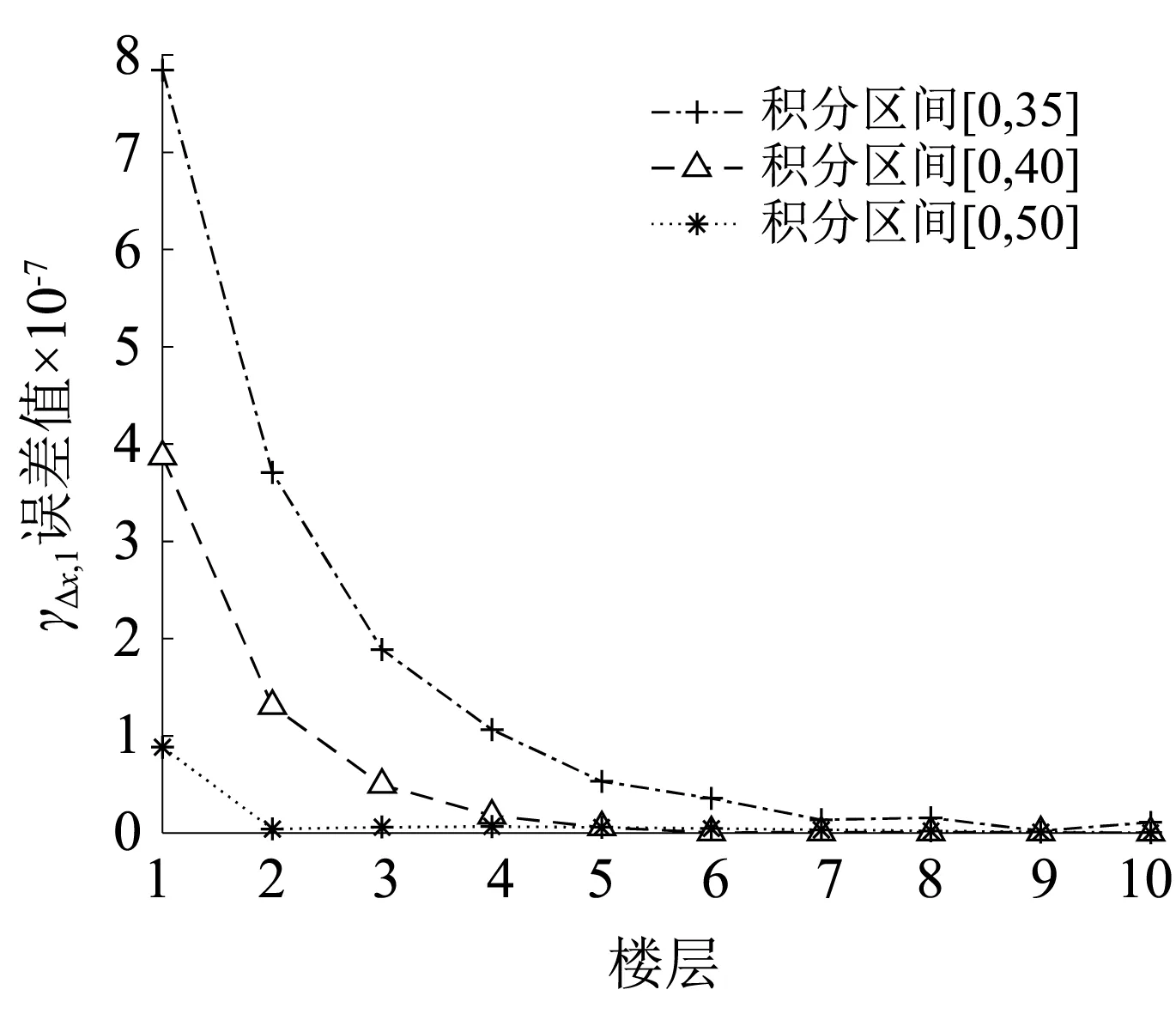
图17 层间位移1阶谱矩误差对比(Δω=0.000 1 rad/s)Fig.17 Accuracy of 1st-order spectral moments(Δω=0.000 1 rad/s)
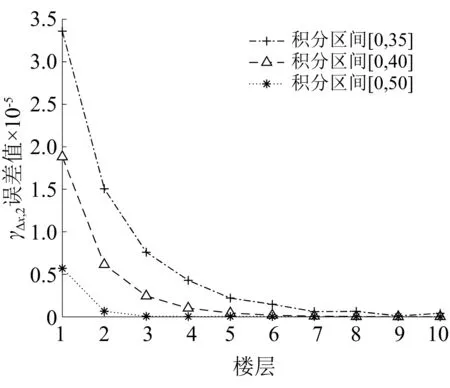
图18 层间位移2阶谱矩误差对比(Δω=0.000 1 rad/s)Fig.18 Accuracy of 2nd-order spectral moments(Δω=0.000 1 rad/s)
基于同一CPU耗时对比,分别用两种方法计算结构位移和结构层间位移的0~2阶谱矩(一共计算10层楼),本文方法耗时0.503 s,虚拟激励法耗时727.178 s,其中,虚拟激励法的ω∈[0, 250],Δω=0.000 1 rad/s。可见,本文方法计算效率有大幅度地提高。
6 结 论
本文对设置广义Maxwell阻尼器的耗能结构基于欧进萍谱随机激励下的响应进行分析,提出了一种简明解析解法,并给出一算例,验证所提方法的正确性和高效性。
(1)利用欧进萍谱滤波方程,重构结构运动方程,并用复模态法解耦,使基于欧进萍谱的激励转化为白噪声激励来表示,进而获得耗能结构功率谱以及结构系列响应谱矩的简明解析解,解的形式为系统特征值的线性组合。
(2)将本文得到的激励功率谱与欧进萍谱传统表达式进行对比,将本文得到的结构响应功率谱与虚拟激励法得到的功率谱进行对比,两者图形均完全吻合,验证了本文方法的正确性。本文所得谱矩解和方差解为无积分运算的解析解,与虚拟激励法相比较,计算精度和计算效率都有显著提高,尤其对复杂工程体系优势更明显。
(3)本文方法适用于具有滤波方程的平稳随机地震响应分析,并可以推广到非平稳随机地震响应分析。
(4)所获得的耗能结构响应的0~2阶谱矩解析解,可为随机地震激励下结构动力可靠度分析奠定基础。
附录A:广义Maxwell阻尼耗能结构的虚拟激励法
(A.1)
引入如下复模态变换
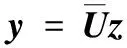
(A.2)
将式(12)改写为
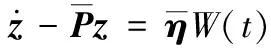
(A.3)
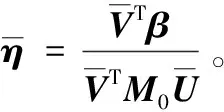
式(A.3)可写成分量形式
(A.4)
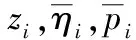
构造一虚拟激励
(A.5)
得结构响应zi(ω)的频域解为
(A.6)
式中:“*”为取复共轭;SW(ω)为白噪声的谱强度。
将式(A.2)和式(A.6)联立,可得第j层结构相对于地面的位移为
(A.7)
(1)结构各层位移功率谱及谱矩
结构各层位移功率谱表达式为
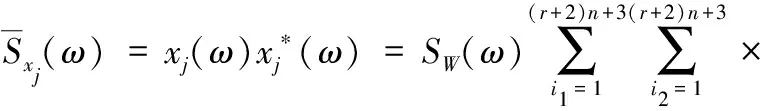
(A.8)
结构各层位移的k阶谱矩表达式为
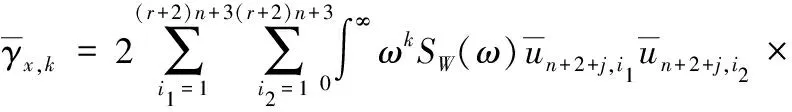
(A.9)
(2)结构各层层间位移功率谱及谱矩
由式(A.7)可知,结构第j层的层间位移为
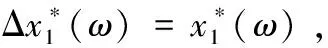
(A.10)
由式(A.10),结构各层层间位移的功率谱表达式为
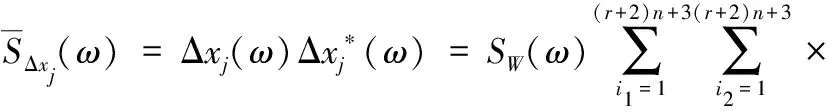
(A.11)
结构各层层间位移的k阶谱矩表达式为
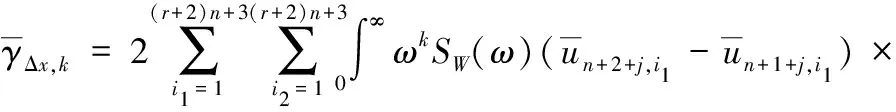
(A.12)

