负刚度吸振器对有限长弹性梁的抑振效果研究

刘海平， 黄志锋， 边新孝

(北京科技大学 机械工程学院，北京 100083)

梁式结构属于工程实际中一种典型结构，如钢轨、输油管道、桥梁、航天器上的展开臂等，由于结构刚度低，阻尼小，振动控制难度大，利用动力吸振器对梁结构的振动进行控制具有重大意义。近年，学者针对动力吸振器对梁结构的振动控制开展过许多研究。Jacquot[1]通过在无阻尼悬臂梁上附加集中参数阻尼器和动力吸振器，研究分布参数系统的最优随机振动抑制问题。Thompson等[2]针对钢轨的横向与垂向振动峰值频段设计了一种由阻尼层与双层质量块构成的动力吸振器。Bae等[3]提出一种改进的调谐质量阻尼器的概念，并针对调谐质量阻尼器对悬臂梁振动响应的控制进行研究。戚健儒等[4]设计短、长两种钢轨试验模型，采用力锤锤击激励方式，对比测试了吸振器安装前后钢轨振动量级及钢轨振动衰减率的变化。张新亚等[5]为了实现对简支箱梁多阶模态参与振动响应的控制，基于调谐质量阻尼器(tuned mass damper,TMD)定点理论及多自由度系统等价质量识别法，得到箱梁结构附加TMD的最优参数。马信欣等[6]将行人激励简化为移动简谐加载，建立人群-人行桥-TMD振动系统，用Simulink对此简支梁桥进行定质量TMD与变质量TMD的减振分析。周笛等[7]基于反共振原理，设计了一种可调频式的管道动力吸振器，将其安装在管路共振位移最大处，可以实现不同频率下管道减振。孙倩等[8]建立包含复合吸振器的弹性车体-轨道耦合垂向动力学模型，该方案可同时实现对车体刚体振动和弹性振动的有效抑制。

随着对振动控制系统的深入研究，学者发现，在动力吸振器中引入负刚度元件能够极大降低共振峰值，同时有效抑振频带更宽。因此，近年针对负刚度动力吸振器的研究获得持续关注。

彭海波等[9]提出一种含有负刚度弹簧元件的新型动力吸振器，通过固定点理论对该类吸振器的最优参数展开研究。王孝然等[10]提出一种含有负刚度弹簧元件的三要素型动力吸振器模型，利用固定点理论和最小化幅频曲线的最大值得到系统的最优参数。Huang等[11]提出一种具有负刚度的动力吸振器来抑制轴系纵向振动的传递；同年，Huang等[12]又采用负刚度动力吸振器控制刚性基础的力传递。郝岩等[13]将黏弹性材料模型中的Maxwell模型引入到吸振系统，形成一种含负刚度元件的Maxwell模型动力吸振器，根据H∞优化准则得到最优参数。Liu等[14]为了降低有碴轨道钢轨部分的振动传递和辐射噪声，研制了一种负刚度钢轨动力吸振器。Zhou等[15]研究动力吸振器与负刚度的两种构型，并根据固定点理论和稳定性最大化准则两种优化方法进行了参数优化。陈杰等[16]提出新型的被动振动控制结构，即含有惯容器和负刚度弹簧元件的动力吸振器振动控制结构，通过理论分析和最优设计证明其可以有效抑制梁的横向振动。

以上针对动力吸振器的研究和优化设计，均是以系统的单点响应或单点传递率作为控制量和评价指标。显然，此类评价方法限于动态信息有限而无法全面评价动力吸振器的振动控制效果。功率流方法综合力和速度响应的大小及相位关系，给出振动传输的一个绝对度量，是研究复杂系统振动的有效工具。

宛敏红等[17]针对附加动力吸振器的简支矩形薄板，利用结构导纳理论，推导出集中简谐力偶作用下系统各环节的功率流表达式。徐振邦等[18]通过子结构导纳综合法建立柔性主系统和有底座吸振器耦合的动力学模型，以系统中的净功率流和振幅为考核指标，探讨底座参数对减振效果的影响。Yang等[19]研究了二自由度系统的振动功率流特性，用解析近似和数值积分方法获得振动系统的时均功率流以及系统的动能，利用功率吸收比和非线性振子的动能，定量地评价非线性吸振器相对于现有非线性振子的有效性。Zhou等[20]通过功率流方法确定时间平均功率流输入和传输的动能，用功率流密度向量表示复合材料板内部的振动传播路径。

综上，现有针对负刚度动力吸振器的研究主要以集中参数模型为主，通过优化设计讨论其振动控制效果。实际中，受工程结构边界条件和动态弹性特征的影响，负刚度动力吸振器的有效性将发生改变。此外，针对此类系统采用单点的响应特征或传递特性无法全面了解其振动控制效果。在此基础上，考虑采用功率流法研究两类负刚度动力吸振器对弹性简支梁动态响应的控制效果。首先，利用所建理论模型，以弹性简支梁的第1阶模态作为振动控制对象，利用固定点理论和最大值最小化理论获得负刚度动力吸振器的最优设计参数。然后，采用功率流理论对安装不同类型动力吸振器弹性简支梁的振动控制效果进行评价。最后，通过对比研究，明确关键设计参数。相关研究为负刚度动力吸振器的工程应用提供一定理论参考。

1 安装负刚度吸振器弹性梁模型

弹性梁为等截面简支梁，弹性模量E，密度ρ0，截面惯性矩I，在距离坐标原点l/4处作用一干扰力P0sin(ωt)，在弹性梁中点布置负刚度动力吸振器。弹性梁水平方向坐标为x，垂直方向坐标为u，坐标原点位于弹性梁左端点，u(x,t)为梁挠度。

此处，重点考虑负刚度动力吸振器安装方式对弹性简支梁动态响应的控制效果，具体模型如图1所示。可见:图1(a)为在传统线性动力吸振器中引入接地负刚度元件；图1(b)为吸振子一端通过弹簧与弹性简支梁连接，另一端则通过并联阻尼元件和负刚度元件与大地相连。

当取消图1中动力吸振器模型的负刚度元件时，负刚度动力吸振器模型退化为传统线性动力吸振器模型,如图2所示。综合图1和图2所建四种模型，论文重点考虑安装不同形式负刚度动力吸振器对有限长弹性简支梁动态响应控制效果的影响。其中:模型3和模型4为传统线性动力吸振器，区别在于阻尼元件安装位置不同；模型1和模型2则分别对应前述两类传统线性动力吸振器的基础上引入负刚度元件。上述四种模型重点从理论角度，研究阻尼元件安装位置和负刚度元件对传统线性动力吸振器振动抑制效果的影响。

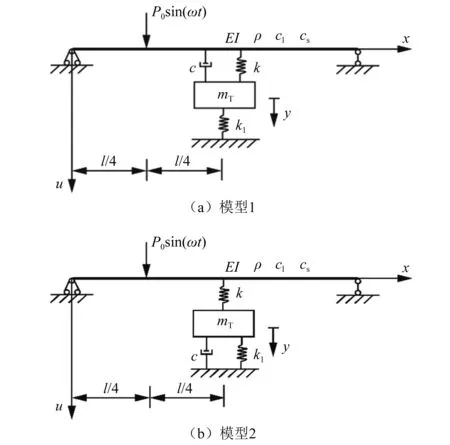
图1 安装负刚度动力吸振器的弹性简支梁模型Fig.1 Elastic simply supported beam models with negative stiffness dynamic vibration absorber

图2 安装传统线性动力吸振器的弹性简支梁模型Fig.2 Elastic simply supported beam models with conventional linear dynamic vibration absorbers

需要说明，上述四种模型均为线性系统，采用随机激励和正弦激励对耦合系统的传递特征影响不大。故，通过采用正弦激励可以得到一些普适性结论。

2 动力学建模

根据图1(a)所示模型，建立系统运动微分方程

(1)

式中：弹性梁的设计参数包括，ρ为单位长度质量，ρ=ρ0bh，b和h分别为宽度和高度，u(x,t)为垂向挠度，δ为Dirac函数，p(x,t)为干扰力；考虑梁的阻尼机理，定义c1为黏性外阻尼系数，cs为应变速度内阻尼系数,其中，c1=aρ，cs=γE，a，γ为比例系数;动力吸振器的设计参数包括，c为阻尼系数，k为正刚度系数，k1为负刚度系数。

采用分离变量法，简支梁的位移表达式

(2)

式中：振型函数可以写成φi(x)=sin(iπx/l)，i=1,2,…，不随时间变化;qi(t)为随时间变化的振幅。

对式(1)两边同时乘以φi(x)，在(0,l)上积，利用振型正交性得到

(3)

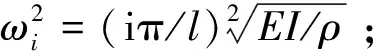
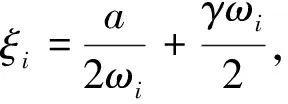
(4)

引入参数

式(3)可以写成

(5)

对式(5)进行拉式变换，设Qi=H1iejωt，Y=H12ejωt，s=jω，可以得到

(6)

引入参数

(7)

可以解得

(8)

引入参数

λ=ω/ωi,ν=ω2/ωi,β=f/Ki

通过式(8)可以得到模型1第i阶模态对应的幅频响应

(9)

式中：F1=αν2+ν2-λ2;G1=2λν;N1=(A2αμν2+1+α)ν2+(-4ξiξν-αν2-A2μν2+λ2-ν2)λ2;M1=2A2αξμν3λ+2αξiν2λ-2A2ξμνλ3+2ξνλ+2ξiν2λ-2ξiλ3-2ξνλ3。

引入振幅放大因子，可以得到

(10)

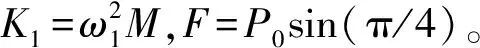
根据图1(b)所示模型建立系统运动微分方程

(11)

采用针对模型1的求解方法，对式(11)进行拉式变换，设Qi=H2iejωt，Y=H22ejωt，s=jω，可以写出模型2第i阶模态对应的幅频响应

(12)

式中：F2=αν2+ν2-λ2;G2=2λν;N2=(4ξiξν+αν2+1+ν2-λ2)λ2+(-A2αμν2-α+A2μλ2-1)ν2;M2=-2αξiν2λ-2A2ξμν3λ-2ξλν-2ξiν2λ+2ξiλ3+2ξνλ3。

引入振幅放大因子，可以得到

(13)

3 功率流

为了评价负刚度动力吸振器对弹性简支梁动态响应的控制效果，从了解系统内部振动能量分布情况出发，采用功率流方法，综合考虑振源输入系统的总功率流、注入主振系的净功率流和动力吸振器消耗的功率流的变化特征，揭示其吸振机理和振动控制效果。

根据功率流的定义，当结构在某点受一简谐激振力P0=|P0|sin(ωt)时，该点的速度响应为V0=|V0|sin(ωt+φ)，则在一个周期内该点的时间平均功率流为

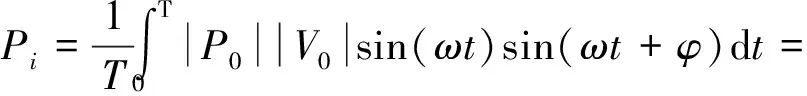
(14)

式中:Yi和Zi分别为结构的点导纳和点阻抗;上标“*”为复共轭。

对于未附加动力吸振器的主振系，输入系统的总功率可以表示为

(15)

对于附加动力吸振器的系统，在激振力作用下，振源输入系统的总功率流为

(16)

式中:i=1，2，…，n为节点数，上标“*T”为复共轭转置。

动力吸振器消耗的功率流为

(17)

式中，PA为动力吸振器在其安装位置引起的吸振力。

根据机械能守恒，可以得到注入主振系的净功率流为

W1,2=W1-W2

(18)

4 计算结果分析

本文重点研究负刚度动力吸振器不同安装方式对弹性简支梁动态响应的控制效果。为了便于分析，选择弹性梁的设计参数如表1所示。

表1 简支梁的设计参数

根据模态叠加理论，弹性结构频响特性主要受前几阶模态影响较大，故为了简化分析过程，此处以弹性梁的第1阶模态作为振动控制对象。其中，第1阶模态对应的模态质量、模态刚度和模态固有频率由式(5)得出。在此基础上，利用固定点理论[21-23]可以求出4个模型中不同形式动力吸振器的最优设计参数表达式如表2所示。系统质量比取值μ=0.05，一般质量比的取值范围为1%～5%。进而，可以得到不同模型对应的最优设计参数如表3所示。

表2 不同动力吸振器模型最优设计参数表达式

表3 不同模型设计参数(质量比μ=0.05)

4.1 频响曲线

利用所建模型及最优设计参数给出安装不同形式动力吸振器弹性简支梁L/4处加载点的幅频响应放大系数曲线,如图3所示。

图3 不同模型对应弹性梁放大系数曲线Fig.3 The elastic beam amplification factor curves for different models

由图3可见，第1阶模态固有频率处，通过引入负刚度元件，在显著降低谐振峰值的同时有效抑振频带更宽。其中，模型2对应负刚度动力吸振器的抑振效果最好。在弹性简支梁第3阶模态固有频率处，四种动力吸振器均可实现不同程度的减振效果，且模型1的减振效果显著。此外，受动力吸振器安装位置影响(位于第2阶模态振型的节点处)，对应弹性梁幅频响应放大系数曲线第2个谐振峰不受影响。

4.2 功率流曲线

采用功率流方法，安装不同形式动力吸振器弹性简支梁的总功率流如图4所示。可见，受动力吸振器影响第1阶模态频率附近共振峰得到衰减；相比传统线性动力吸振器，考虑负刚度元件的影响对应系统总功率流曲线共振峰值被进一步衰减。

图4 不同模型对应弹性梁总功率流曲线Fig.4 The elastic beam total power flow curves for different models

同样地，图5给出不同安装形式动力吸振器消耗的功率流。由图显见，在传统线性动力吸振器中插入负刚度元件可以显著增加其功率消耗能力。

图5 不同模型对应动力吸振器消耗功率流曲线Fig.5 The dynamic vibration absorber power flow consumption curves for different models

从功率流的角度，选择净功率流作为评价不同形式动力吸振器对弹性简支梁幅频响应振动控制效果的指标，计算结果如图6所示。可见，在弹性简支梁的第1阶模态固有频率处四种动力吸振器均可实现不同程度的减振效果，且模型1和模型2的减振效果显著。产生该现象的原因在于动力吸振器中引入了负刚度元件[24]。在弹性简支梁第1和第2阶模态固有频率之间的较宽频带内，负刚度动力吸振器的减振效果明显优于线性动力吸振器。在弹性简支梁第3阶模态固有频率对应谐振峰处，四种动力吸振器均可实现不同程度的减振效果，且模型1的减振效果最显著。

图6 不同模型对应弹性梁净功率流曲线Fig.6 The elastic beam net power flow curves for different models

4.3 时域响应

实际中，系统所受环境激励呈现多频宽带特征，为了研究负刚度动力吸振器对弹性简支梁动态响应的振动抑制效果，在时间域展开讨论。假设弹性简支梁所受外激励F=∑sin(ωit)，ωi=8 rad/s，ωi=35 rad/s，ωi=78 rad/s，ωi=138 rad/s，ωi=216 rad/s，ωi=312 rad/s。

弹性简支梁L/4处加载点的位移为

(19)

引入参数

Ust=φ1(L/4)Hst，Ust为弹性简支梁L/4处加载点的静态位移。

对弹性简支梁L/4处加载点的位移进行无量纲处理，得到

(20)

图7给出多频力激励条件下，安装不同形式动力吸振器弹性简支梁L/4处加载点的位移时程响应曲线。由图可见，安装负刚度动力吸振器弹性简支梁的振动控制效果明显优于安装线性动力吸振器弹性简支梁。而且，模型2的振动控制效果最优。

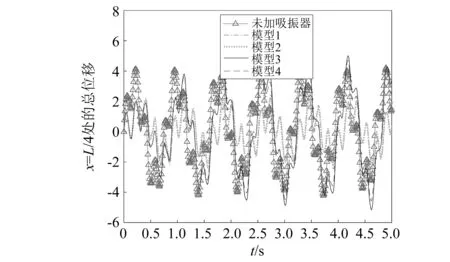
图7 不同模型对应弹性梁位移时程曲线Fig.7 The elastic beam displacement and time seriescurves for different models

5 影响因素分析

根据前述内容的分析，模型2对应负刚度动力吸振器对弹性简支梁第1阶模态振动响应的控制效果最好。因此，本章重点针对该类负刚度动力吸振器的设计参数进行影响分析，具体包括：弹性简支梁长度L，质量比μ，刚度比α、阻尼比ξ及外部激励加载位置。

5.1 弹性简支梁长度L的影响

图8给出弹性简支梁长度变化对负刚度动力吸振器振动抑制效果的影响。由图可见，随着弹性梁长度增加，结构刚度降低故第1阶模态固有频率向低频移动，且第1阶模态固有频率处消耗的功率峰值增大对应有效抑振频带变窄。可见，负刚度动力吸振器在第1阶模态固有频率处的减振效果仍然显著。此外，弹性简支梁长度越小，振动控制效果越好。

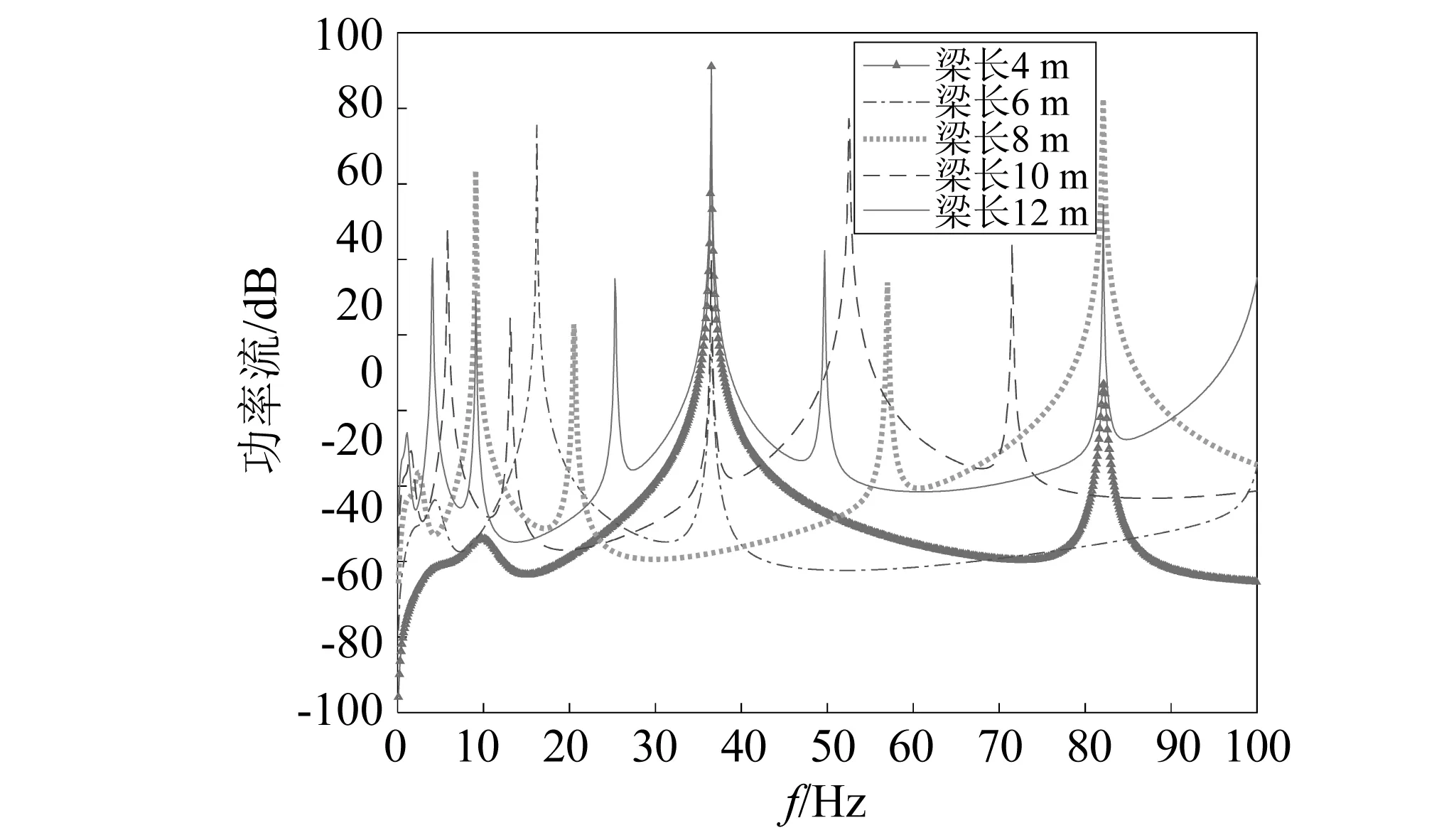
图8 弹性简支梁长度对功率流的影响Fig.8 The influence of elastic simply supported beam length on power flow

5.2 质量比μ的影响

负刚度动力吸振器质量比变化对其振动控制效果的影响如图9所示。从图中可以看出，随着质量比增大，减振效果变好。但是，考虑工程实际，负刚度动力吸振器附加质量增加范围有限。

图9 质量比对功率流的影响Fig.9 The influence of mass ratio on power flow

5.3 刚度比α的影响

图10给出刚度比变化对负刚度动力吸振器振动控制效果的影响。可见，在第1阶模态固有频率处，最优刚度比在(-0.7,-0.6)内；在(-0.6,0)内，随着刚度比的增加，在第1阶模态固有频率处的功率峰值增大，且有效抑振频带变窄。此外，在第3阶模态固有频率处，刚度比在(-1,-0.7)内，随着刚度比增加，减振效果变好；在(-0.7,0)内，随着刚度比增加，第3阶模态固有频率处的功率峰值增大。

图10 刚度比对功率流的影响Fig.10 The influence of stiffness ratio on power flow

5.4 阻尼比ξ的影响

图11给出不同阻尼比对应安装负刚度动力吸振器弹性简支梁的功率流曲线。对比可见，在第1阶模态固有频率处，最优阻尼比在(0.2,0.4)内；在(0.3,1)内，随着阻尼比增加，对应弹性简支梁第1阶模态固有频率处功率峰值变大，有效抑振频带变窄。在第3阶模态固有频率处，随着阻尼比增加，减振效果变好；但是，在工程上，阻尼比不是越大越好，针对负刚度动力吸振器的阻尼比需要考虑实际应用条件。

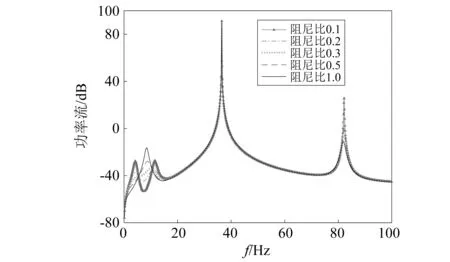
图11 阻尼比对功率流的影响Fig.11 The influence of damping ratio on power flow

5.5 激励位置的影响

图12给出不同外激励加载位置变化对安装动力吸振器弹性简支梁功率流的影响。由图可见，随着激励位置从L/8递增到L/2，在第1阶模态固有频率处的功率峰值变大；在第2阶模态固有频率处，激励位置在L/4处的功率最大，在L/2处无功率峰值；随着激励位置从3L/8递减变化到L/8，在第3阶模态固有频率处的减振效果变差，在L/2处的功率最大。

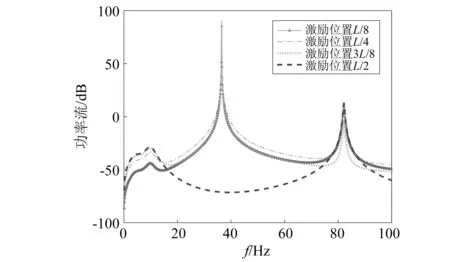
图12 加载位置对功率流的影响Fig.12 The influence of loading location on power flow

需要注意，当外激励加载位置和动力吸振器安装位置相同且位于简支梁模态振型的波腹时，则振动控制效果最好。

6 结 论

为了研究负刚度动力吸振器不同安装方式对弹性简支梁动态响应的影响，本文分别提出四种不同类型动力吸振器与弹性简支梁的组合模型。在此基础上，以弹性梁的第1阶模态作为振动控制对象，利用固定点理论获得安装不同形式动力吸振器简支弹性梁模型的最优设计参数。利用功率流作为动力吸振器振动抑制效果的评价指标。根据计算结果，可得到以下结论：

(1)针对目标模态频率附近，负刚度动力吸振器对弹性简支梁的振动抑制效果显著优于线性动力吸振器；且，模型2对应的负刚度动力吸振器振动控制效果最好。

(2)以弹性梁的第1阶模态作为振动控制对象获得动力吸振器的最优设计参数，受其弹性特征影响对第1阶模态响应的振动控制效果较好。

(3)将安装典型负刚度动力吸振器弹性简支梁(模型2)功率流作为评价指标，针对主要设计参数进行影响分析发现均存在最优值。