在PLZN环境下基于组内优势关系的TODIM-PROMETHEE决策方法

朱蒙蒙， 毛军军,2， 徐 威

(1.安徽大学 数学科学学院，合肥230601；2.安徽大学 计算机智能与信号处理教育部重点实验室，合肥230039)

0 引 言

MCGDM(多准则群决策方法)是指一群决策人(个人或者群体)，按照各自的偏好，在共同的准则下，对不同的备选方案进行评价，以寻求群体满意的目标。TODIM方法是一种著名的基于前景理论[1-2]的MCGDM方法。它考虑了人在风险和不确定环境下的心理行为。由Brans和Vincke[3]提出的PROMETHEE方法也是一种常用的MCGDM方法，方法基于对标准备选方案的两两比较。PROMETHEE II法是PROMETHEE方法的一种，具有排序完整性的优点。许多学者对两种方法都有不同方向的扩展以及应用[4]。传统的TODIM方法与PROMETHEEⅡ都有其自身的局限性，为克服这种不足，有学者提出了传统方法融合的决策方法[5]。这种新的决策方法不仅使得两种传统方法发挥了各自的优点，同时还能将各自的不足很好的互补。

Z-number是Zadeh[6]开发以克服传统语言型模糊数无法表达决策信息可靠性这个缺点的。Z-number的第一个组成部分是模糊约束，通过不确定的语言变量来描述。目前，Z-number及其扩展通常使用单个语言项、多个语言项和区间语言项来描述模糊约束，但它们的描述不适用于群体决策信息。PLZN(概率语言型Z-number)是对传统语言型Z-number的改进，充分考虑了各项语言集出现的概率，比起Z-number，PLZN环境更加适合群体决策。

然而，考虑专家(决策人)的专业知识与专业背景不同，不同的专家提供的信息可靠度也是不同的。如何有效地将专家可信度的差异融入决策中是深入研究的重点。另外，准则的权重直接依靠专家的主观赋值，不够客观稳定，更合理的权重赋予方式也是值得多加考虑的。为了解决以上的问题，选择先对同一准则下同一专家评价可信度的组内进行融合，充分考虑组内优势关系以及组内的差距；其次，在考虑组间差距的同时对不同组的信息进行合成。在此基础上利用使组间偏差达到最大的方法得到的权重，不仅考虑了方案之间的差距，也考虑了不同专家组之间的差距。

1 预备知识

定义1[6](Z-number)Z-number是一对与实值不确定随机变量X相关的有序模糊数(A,B)，其中A是对X可以取到的值的模糊限制，B是对A的可靠性度量。通常情况下，A与B通过自然语言描述，例如(非常好，有可能)。

定义2[7](LTS)令S={si|i=0,1,2,…,2g,g∈N+}是一个语言术语集(LTS)，其中si表示语言变量的一个可能值，并且满足条件：

S是有序的：α>β⟺sα>sβ

存在否定运算符：neg(sα)=s2g-α。

定义3[8](PLTS)令S={si|i=0,1,2,…,2g,g∈N+}是一个LTS，那么PLTS被定义为

L(p)={hi(pi)|hi∈S,pi≥0,

其中hi(pi)代表语言变量hi和其对应的概率pi，#L(p) 是L(p)中语言变量的个数。

定义4[9](LSF)令S={si|i=0,1,2,…,2g,g∈N+}是一个LTS，其中si∈S是一个语言变量，定义LSF是将si映射到θi的函数f即：

f:si→θi(i=0,1,2,…,2g)

其中θi∈[0,1]。显然，f是一个对于下标i严格单调递增的函数。

定义5[5](PLZN)在论域X中，L(p)={ho(p0),h1(p1),…,h2m(p2m)}是一个离散且有序的PLTS并且L={l0,l1,…,l2n}是一个离散且有序的LTS，其中hi,li是语言集，pi是概率，m,n∈N+。X的PLZN定义为

Z={(x,Az(x),Bz(x))|x∈X}

其中Az(x)是L(p)的一个子集，是对X可以取到的值的一个模糊限制，Bz(x)是L中的一个元素，是对Az(x)的可靠性度量。对于一个特定的变量α，其PLZN被表示为：zα=(Az(α),Bz(α))。

2 组内优势关系与组内偏离度

定义6 (影响因子、附加因子、敏感因子)

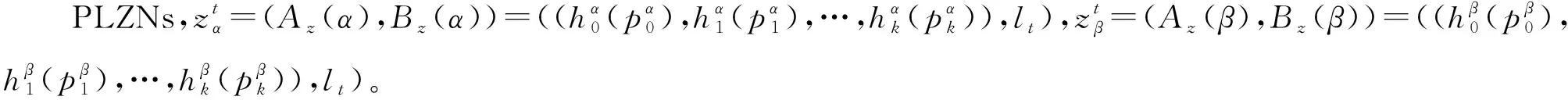
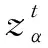
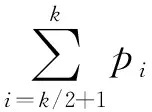
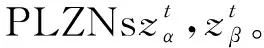
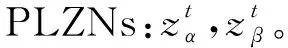
其中，k∈2m,t∈2n，其中，f(*)是LSF。

定义9(综合偏离度)对于准则cj下方案α与方案β的综合偏离度定义为

其中，g(*)是LSF。

定义10(综合优势度)对于准则cj下方案α与方案β的综合优势度定义为

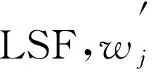
3 一种新的TODIM-PROMETHEE Ⅱ决策流程

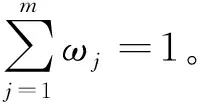
Step1 收集决策者的评价并将其转化为PLZNs。

Step2 根据组内优势关系、组内偏离度计算综合偏离度。

Step3 计算权重向量。

考虑利用一种扩展的最大偏差方法来计算权向量。与其他的权重确定方法相比，扩展的最大偏差法[10-11]利用各准则下各备选方案的整体偏差来确定准则权重，充分考虑了各评价信息之间的内在关系。具体的过程如下：

(1)

其中DVj(zij,zkj)是zij,zkj两个PLZNs之间的综合偏离度。

构造Lagrange函数以求解权重ωj，

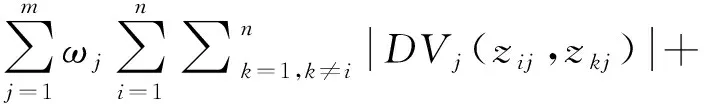
(2)

其中λ为lagrange乘子，通过对F(ωj,λ)求偏导得到以下等式：

(3)

通过计算式(3)，得到准则的最优权重如下：

(4)

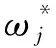
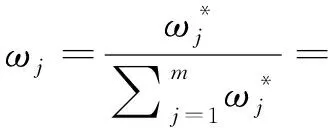
(5)

Step4 确定所有准则的标准权重。

根据式(6)计算准则的标准权重：

(6)

其中ωr=max (ωj|j=1,2,…,m)。

Step5 计算某准则下综合优势度。

对于准则cj下方案ai与方案ak的综合优势度为

(7)

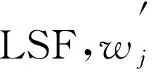
Step6 计算在所有准则下的总体优势度。

在Step5的基础上，总体优势度可通过式(8)求得：

(i,k=1,2,…,n;i≠k)

(8)

Step7 获得流出Φ+(ai)、流入Φ-(ai)以及净流Φ(ai)。

流出、流入与净流分别通过式(9)、式(10)、式(11)计算：

(9)

(10)

Φ(ai)=Φ+(ai)-Φ-(ai)

(11)

其中i=1,2,…,n。

Step8 对评价目标进行排序。

根据判决规则，Φ(ai)越大说明方案ai越优。

4 实例分析与应用

4.1 计算过程与结果

根据上述决策步骤，得到综合偏离度。再根据式(1)—式(5)，采用最大偏差法确定的归一化后的最优权重如图1所示。

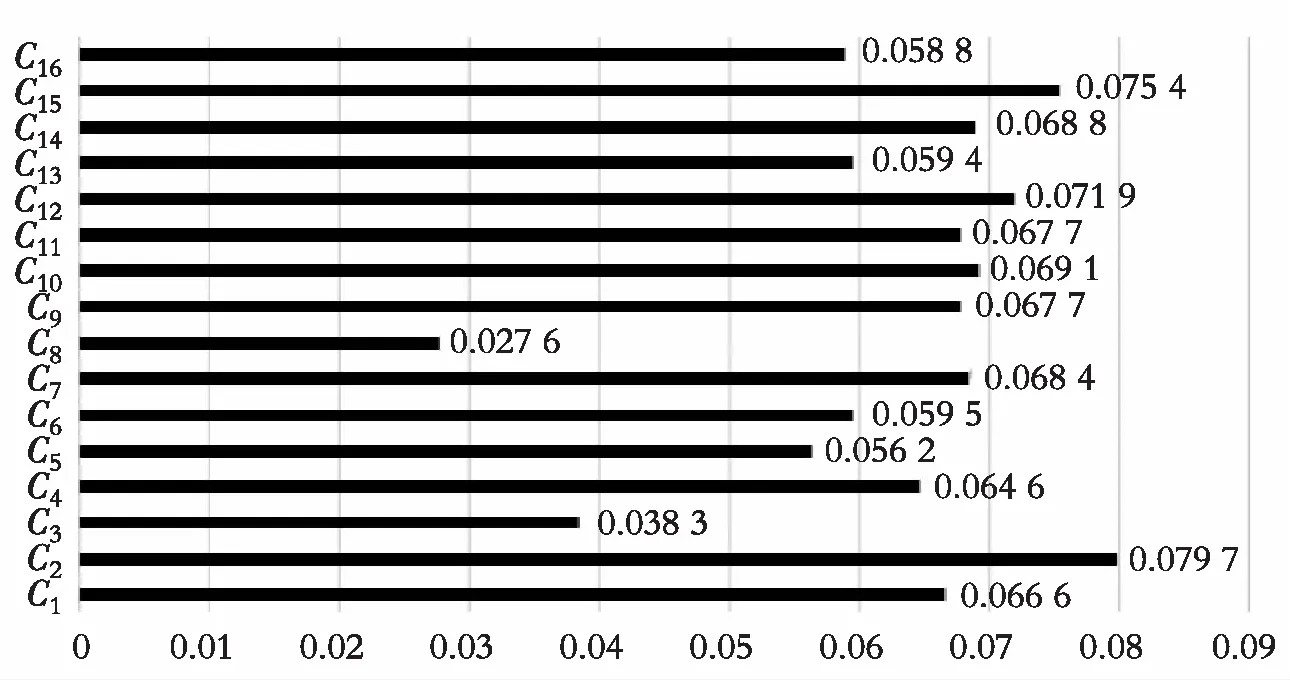
图1 16个准则的权重比较Fig. 1 The weight comparison among sixteen criteria

通过式(6)确定所有准则的标准权重，如表1：

表1 各个准则的标准权重Table 1 The standard weight of each criterion

根据式(8)计算得到所有准则下的总体优势度，结果如下：

根据式(9)-式(11)计算得到流出Φ+(ai)、流入Φ-(ai)以及净流Φ(ai)，结果如表2所示：

表2 流出、流入与净流Table 2 Outflows， inflows and netflows

根据净流大小，获得最终方案排序为a1≻a6≻a5≻a3≻a2≻a4，因此慈利县应当作为优先治理地区。

4.2 比较分析

对比原参考文献的结果，差异来源主要在于优先定义的同一组专家评价内的优势关系。先验的优先顺序很大程度上影响了最终的结果。在定义的的组内优势关系中，敏感因子也对最终结果起着一定程度的影响，使得新定义的组内优势关系有着很强的可变性和适应能力。对于不同的敏感因子，结果差异如表3所示。

表3 不同敏感因子对应结果对比Table 3 Comparison of the results of different sensitive factors

由表3可知：方案1随着劣性评价(ε2)占比的增加，排名向后移动；方案2随着优性评价(ε1)占比的增加，排名向前移动；方案3随着劣性评价(ε2)占比的增加，排名向前移动。

5 结束语

在PLZN环境下，对优势度计算进行了改进，提出了一种新的优势关系，区别于同一方案内不同评价可信度先融合的决策步骤，先对同一评价可信度的组内信息进行融合，得到组内偏离度，再根据专家评价的可信度对不同等级的专家评价进行融合得到综合优势度。再基于TODIM与PROMETHEEⅡ两种决策方法互补结合的决策方法，最终得到方案的排序。在这里，由于综合优势度是基于先验的优势关系与偏离度，从而最终的决策结果与先验信息有密不可分的关系。如何得到更加准确的先验信息有待深入研究。