基于事件触发的二阶多智能体时滞一致性
韩 琦, 王 霞, 王 慧, 袁艺云, 曹 瑞, 翁腾飞
(1.重庆科技学院 智能技术与工程学院, 重庆401331; 2.重庆师范大学 数学科学学院,重庆 401331;3.重庆科技学院 电气工程学院,重庆 401331)
0 引 言
近些年来,随着多智能体的协同控制在各个领域得到应用,多智能体系统的协同控制受到了众多研究者的广泛关注[1-3]。其中研究得最多的就是一致性问题,利用多智能体的一致性可以应用到编队控制、智能电网经济调度[4]等问题。在多智能体的系统控制中,研究者多数是采用分布式控制协议,与集中式协议相比,分布式控制中单个个体设计简单,且个别的智能体的失效不会影响全局,最重要的是分布式控制拥有协作好、灵活性高、信息交流少、应用性强等优势[5]。
到目前为止,多智能体一致性问题已经得到众多学者的深入的研究,文献[6]结合分布式事件触发机制考虑了一种带有容错性质的自适应一般线性多智能体系统。但是在很多研究中都会发现,网络中的信息流通常不是即时的,会存在时间的延迟。时滞一致性意味着跟随者的状态与领导者的相应状态有一段时间延迟。在以往的研究中,针对时滞问题,有很多研究者主要集中在对时滞下系统的收敛性[7]和一致性[8]加以讨论。且在存在时滞的系统中,不同孤立群集中的智能体在不同时刻的状态都落后于它们的共同领导者,从而避免了在容量受限网络上运行的多智能体系统的拥塞。为了确保系统时滞一致,并在一定程度解决信息流拥塞问题。
基于以上的启发,考虑事件触发机制作为信息传输策略。因为事件触发机制避免了控制器的连续更新问题,不仅减少了网络中的数据量,而且延长了网络组件的使用寿命。现如今事件触发在很多领域得到利用,在文献[9]中研究了一种关于事件触发的双边非线性的二阶多智能体系统,该系统可利用事件触发达到竞争下多智能体分组的一致,增加了事件触发的范围。文献[10]考虑了关于事件触发中具有干扰的主动控制的多智能系统,并且该系统实现了一致性。综合时滞和事件触发这两方面,讨论具有事件触发的二阶领导-跟随多智能体时滞一致性问题。
主要贡献可归纳为如下方面:
(1) 考虑具有领导者的二阶非线性多智能体系统,通过设计一种关于时滞一致性的事件触发控制器,相比文献[11],有效结合事件触发机制,减少了不必要的计算,降低了成本。
(2) 针对触发控制协议,给出了相应的触发条件,和利用图论、矩阵理论和Lyapunov稳定性方法,给出了保证多智能体系统达到时滞一致的充分条件。最后利用微分方程理论和范数不等式理论,得到了本文设计的事件触发协议是可以避免Zeno 行为。
1 预备知识
1.1 图论理论
用带有N个节点的有向图G={V,Ε,W}表示由N个多智能体构成的多智能体系统。定义i,j=1,2,…,N,那么其中V={v1,v2,…vi,…vN}表示为节点集,vi表示第i个多智能体;E={eji=(vi,vj),vi≠vj,且vi∈V,vj∈V}⊆V×V代表边缘的集合,相应的(vi,vj)表示节点vi可以接受来自vj的信息,而且如果图G被称为强连通图,则对于任意两个节点都存在有向路径来达到连通。W=(wij)N×N表示节点与节点之间的邻接矩阵。如果(vi,vj)∈E,∀vi,vj∈V,则wij>0,否则wij=0。图G中的Laplace矩阵L=[lij]∈Rn×n满足下列定义
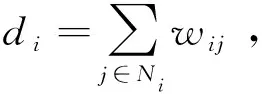
1.2 符号标注
IN表示n维单位矩阵;IN=[1,1,…,1]T∈Rn;‖·‖表示欧氏空间的欧氏距离;矩阵的范数为‖A‖=sup{‖Ax‖:‖x‖=1};⊗表示克罗内克积;对于对称矩阵Y,Y>0(Y<0),表示矩阵Y∈Rn×n是正定矩阵(负定矩阵),λmax(Y)表示矩阵Y的最大特征值,λmin(Y)表示最小特征值。
1.3 问题描述
研究一个领导者和N个跟随者构成的二阶非线性多智能体系统,其中领导者的系统形式描述如下:
(1)
跟随者的系统形式:
(2)
其中,xi(t)∈n,vi(t)∈n,ui(t)∈n(i=0,1,2,…,N)分别表示智能体i在时间t时的位移,速度和控制输入,并且f(t,xi(t),vi(t))∈n是第i个智能体的非线性函数。
定义1在式(1)和式(2)中,智能体的系统达到二阶领导-跟随时滞一致,当且仅当对于任何初始状态,满足
其中,τ是正常数。
假设1存在非负常数ξ1和ξ2,使得f(t,xi(t),vi(t))满足利普希次条件
‖f(t,x,v)-f(t,y,z)‖≤ξ1‖x-y‖+
ξ2‖v-z‖∀x,y,v,z∈n,t∈[0,∞)
假设2领导者和N个智能体之间至少存在一个有向的生成树,且该网络拓扑图是一个连通图。
引理1[21]线性矩阵不等式:
其中,Q(x)=QT(x),R(x)=RT(x),上述不等式成立时,可以转化为其中一个下面的等价条件:
(1)Q(x)>0,R(x)-ST(x)Q-1(x)S(x)>0;
(2)R(x)>0,Q(x)-S(x)R-1(x)ST(x)>0。
引理2[22]如果矩阵H∈N×N是非奇异矩阵,并且H的非对角元素是非正数,则下面叙述的结论互相等价:
(1)H是一个非奇异的M-矩阵;
(2)H的所有特征值是在平面的右半平面,意味着J(H)>0;
(3) 存在一个正定的对角矩阵P=diag{p1,p2,…,pN}>0,使得有PH+HTP>0成立。
基于事件触发控制定义(2)的控制协议如下
(3)
其中,σ>0是控制增益,τ是正常数。
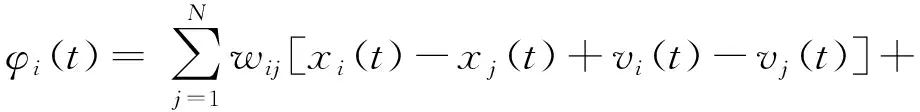
定义触发误差为
一致性误差分别是
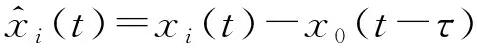
选择触发函数
(4)
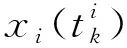
接下来结合一致性误差、事件触发误差和事件触发的控制改写系统式(1)和式(2)如下:
(5)
令
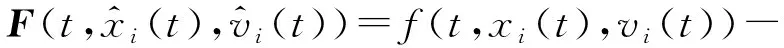

2 主要结论
这部分运用矩阵理论来证明事件触发下的领导跟随者的时滞一致问题,并排除Zeno行为。
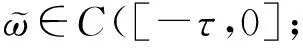
则多智能体系统式(1)和式(2)可以实现领导跟随的滞后一致性。
证明设定V函数如下:
其中,Q=P(L+B)+(L+B)TP。
V(t)对t求导有
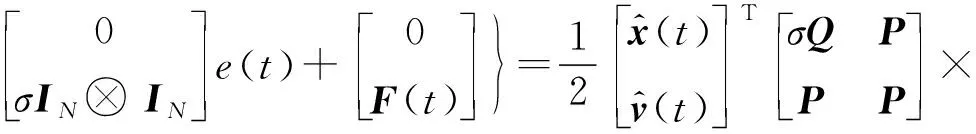
(6)
对于式(6)的最后一项有
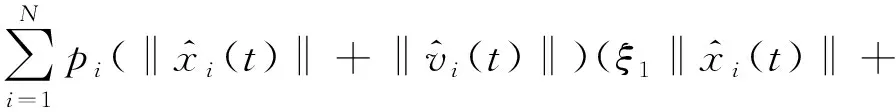
(7)
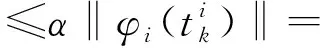
α‖φi(t)+ei(t)‖≤
α‖φi(t)‖+α‖ei(t)‖
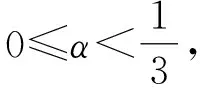
bi(xi(t)-x0(t-τ)+vi(t)-v0(t-τ))‖ =
则对于式(6)的第二项有下列式子
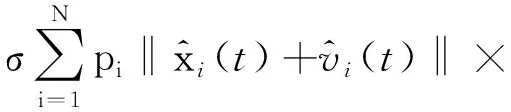
(8)
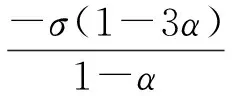
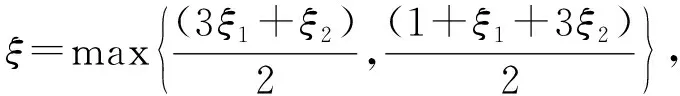
(9)
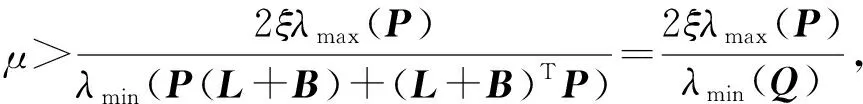
-μ(P(L+B)+(L+B)TP)⊗IN>2ξ(P⊗IN)
即-μ(P(L+B)+(L+B)TP)>2ξP。
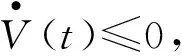
定理2领导跟随多智能体系统式(1)和式(2)利用事件触发函数式(4)和控制式(3)达到时滞一致是可以排除Zeno行为的。
证明
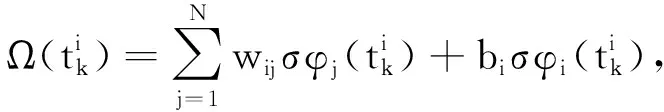
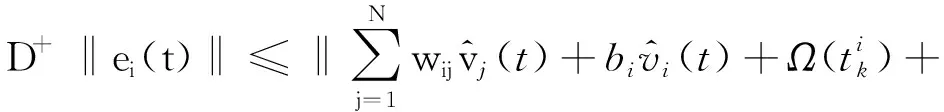
所以,

取ξ=max{ξ1‖L+B‖,(ξ2+1)‖L+B‖},则
(10)
又在式(9)中令,有Ξ>0,可得
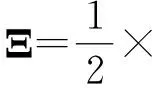
故
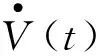
-λmin(Ξ)ηT(t)η(t)。
令
有V(t)=η(t)Ψη(t)。
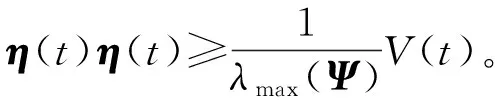
故有
(11)
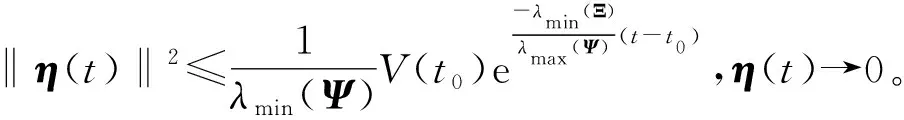
故由式(10)有
即
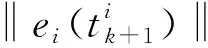
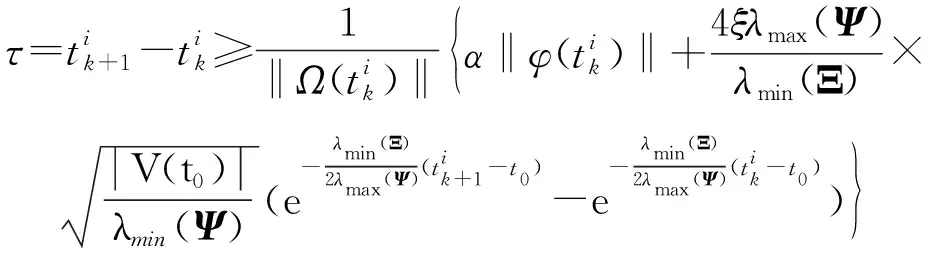
3 实验仿真
考虑4个跟随者和一个领导者的非线性的二阶系统,其中0表示领导者,相应的跟随者网络拓扑如图1所示。
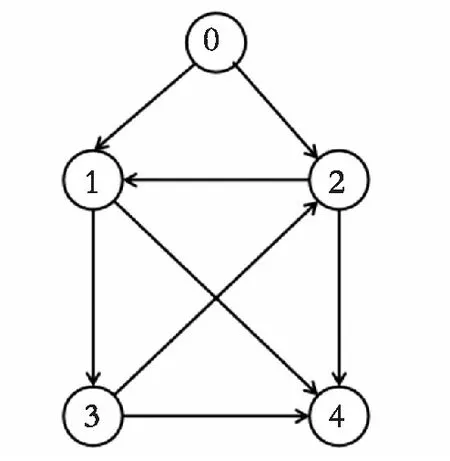
图1 跟随者与领导者结构拓扑图Fig. 1 Communication topology of leader-follower system
其中,Laplace矩阵表示为


从图2和图3可以看出,4个跟随者是可以和领导者达成滞同步一致的。而从图4可以得到,每个智能体的误差曲线,最后都会趋于0,说明跟随者会和领导者趋于一致。图5表明了智能体的控制变化趋势,最后也是每个智能体都是当时间趋于无穷时控制趋于0,充分说明了智能体的时滞一致性。图6是每个跟随者的触发间隔,从图中可以明显看出该触发事件是没有Zeno行为的。图2—图6都有效说明理论的正确性。
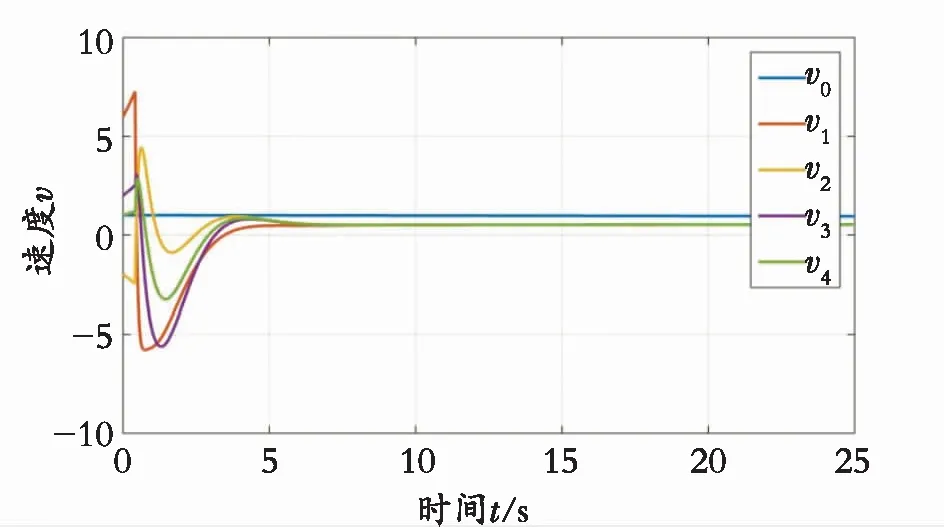
图2 智能体速度变化轨迹图Fig. 2 The velocity trajectory of agent
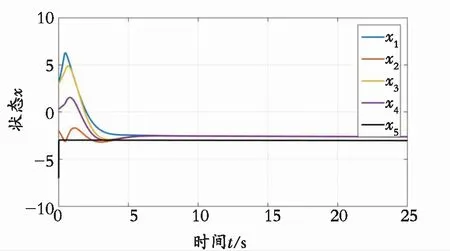
图3 智能体的状态轨迹图Fig. 3 The state trajectory of agent
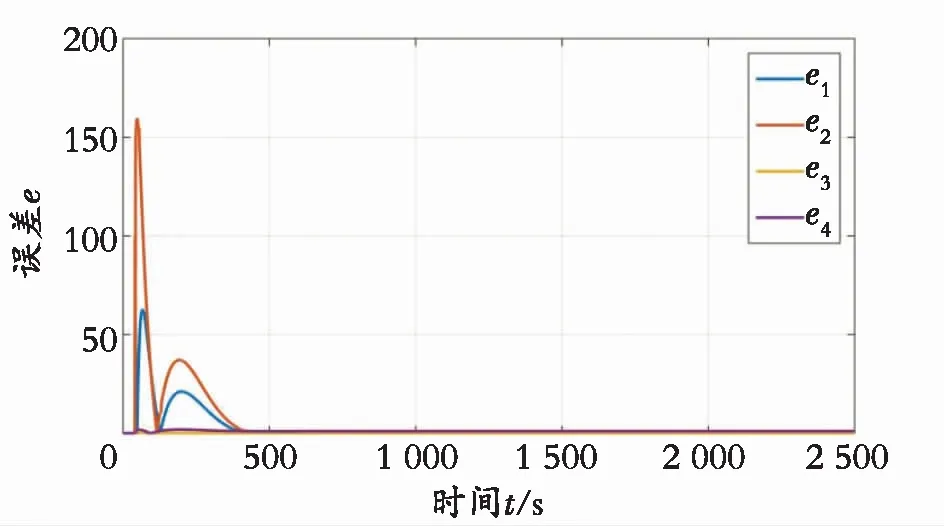
图4 跟随者的误差趋势变化Fig. 4 Error trend of followers
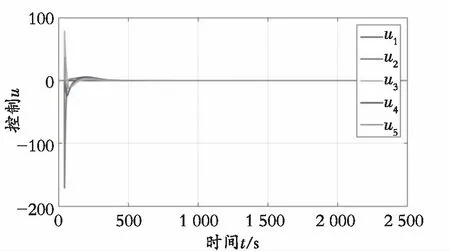
图5 智能体的控制输入变化趋势Fig. 5 Control input trend of agent
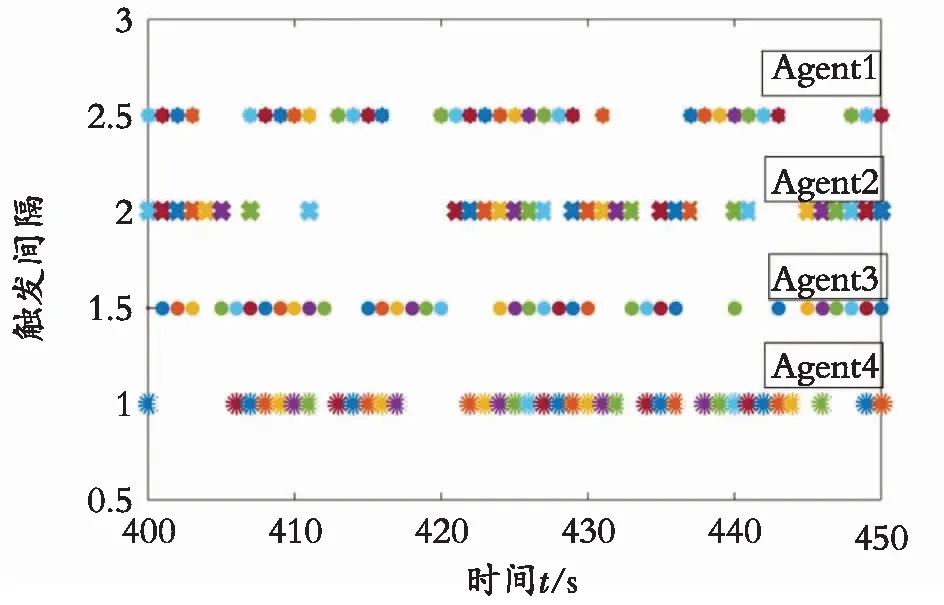
图6 跟随者触发间隔图Fig. 6 Follower trigger interval graph
4 结束语
主要研究智能体的非线性动力学系统,考虑具有时滞效应的二阶领导——跟随多智能体的系统的时滞一致性。首先,结合事件触发机制给出一个基于局部信息的分布式控制协议;然后在这个协议下,运用Lyapunov稳定性理论,图论等相关知识导出该系统实现滞后一致性的充分条件;最后,数值模拟验证理论结果的正确性。
—— 瓮福集团PPA项目成为搅动市场的“鲶鱼”

