基于含测量误差半参数模型的糖尿病数据研究
孙 兴, 黄振生
(南京理工大学 理学院,南京 210094)
0 引 言
在医疗领域,糖尿病是备受关注的慢性病之一,也是全球严重的公共卫生安全问题之一,它除了会给患者带来痛苦之外,还会给家庭和社会带来巨大的经济负担和压力。根据国际糖尿病联盟(IDF)2017的调研结果显示,全球共有约4.25亿糖尿病患者,其中中国糖尿病患者占比超25%[1]。研究糖尿病与体质测量数据之间的关系,可以更好地了解和预防糖尿病,因此具有较为重要的意义。研究的糖尿病数据集包含442个观测样本,其中响应变量是糖尿病患者的定量测量数据,协变量分别为年龄(Age)、性别(Sex)、体质指数(BMI)、平均血压(BP)和6种血清指标测量数据,分别以符号TC、LDL、HDL、TCH、LTG和GLU表示。
部分变系数单指标模型(PVCSIMs)是一类重要的半参数模型,它不仅保留了非参数模型的特点,还能避免“维数灾祸”问题,因此是统计分析的重要工具,尤其在处理高维数据时十分有优势,模型的结构如下:
Y=θT(U)Z+g(βTX)+ε
(1)
可以看出,该模型具有一般性,它不仅兼有变系数模型和单指标模型的特点,还包含了许多其他重要的半参数模型作为特例:对于变系数部分,函数θ(·)表示的是Z和U的相互作用,如果假设θ(·)是常数向量,那么模型就可以看作是部分线性单指标模型,若进一步令系数函数向量θ(·)的维数q等于1,那么就可以得到单指标模型。对于单指标部分,若令联系函数g(βTX)≡βTX,那么模型就变成了部分线性变系数模型,进一步取参数β的维数p为1,模型就退化成了变系数模型。
近年来,关于模型式(1)的研究成果已经十分丰富。为了研究化学污染物水平与每天因呼吸系统疾病住院的总人数的关系,以及温度和相对湿度对入院人数的影响,Wong等[2]首次提出PVCSIMs,他们结合二元局部线性方法、平均方法和一步回拟技术(One-step Back-fitting Technique)得到函数和参数的有效估计。基于他们的研究,Huang和Zhang[3]进一步利用广义似然法(GLR)解决了模型中变系数部分的检验问题。Li和Zhang[4]通过将系数函数和联系函数样条化,提出了模型的惩罚样条估计方法,该方法可以同时得到未知参数和函数的估计值。Wang和Xue[5]的研究指出,Wong等[2]用二元局部线性光滑进行估计可能会导致估计量不相合,因此,提出一种较为稳定的逐步估计法对模型进行估计,其基本思想是:假设参数已知,将模型转换成变系数模型,并利用Nadaraya-Watson核估计方法和局部线性回归方法逐步得到系数函数和联系函数的初步估计,然后根据这些初始估计量计算未知参数的估计值,文章还讨论了估计量的渐近性质,并且建立了逐点置信区间和置信域。Huang[6]通过经验似然方法研究了单指标参数的极大似然估计,并且利用截面经验似然方法构造了各参数分量的置信区间。Huang[7]等结合SCAD(Smoothly Clipped Absolute Deviation)惩罚和逐步估计法研究了指标参数β的变量选择问题,在一定的正则化条件下,还构建了估计量的大样本性质。最近,受到图像数据分析的启发,Li等[8]讨论了函数型数据下PVCSIMs的估计问题,利用局部线性方法逐步迭代得到了系数函数、联系函数、指标参数以及方差函数的估计值,并且证明提出的方法相较于Wong等[2]和Wang和Xue[5]中的方法更加稳定。
虽然半参数模型可以用来解决大部分回归拟合问题,然而在实际应用中,由于操作人员的失误和测量工具不精确等问题,收集到数据中往往带有测量误差,因此进一步研究半参数误差模型是很有必要的。扭曲测量误差(Distorted Measurement Error)作为误差的常见形式,是近年来学者们研究的热点问题。Sentürk 和 Müller[9]提出协变量调整回归(Covariate-adjusted Regression, CAR)模型,即假设响应变量和协变量都含有扭曲测量误差,通过将线性误差模型转换成变系数模型,并结合分箱法给出了对未知参数的估计。Cui等[10]提出一种非参数误差回归模型的一般估计方法,该方法通过核估计得到误差函数的估计量并以此计算受污染变量的校正值,然后根据校正后的变量对目标参数进行估计。Delaigle[11]等进一步讨论了在不同假设条件下非参数误差回归模型的估计问题,在弱化对未知变量或扭曲函数的假设后,提出了更一般的估计方法,并且建立了相应估计量的渐近性质。此外,Qian和Huang[12]研究了含扭曲测量误差的部分非线性变系数模型的统计推断问题。Dai和Huang[13]将协变量含扭曲测量误差的情形推广到部分非线性变系数模型。
对于糖尿病数据集,根据数据本身的特点,利用单指标部分含扭曲测量误差的PVCSIMs模型进行拟合。该模型具有复杂的结构,可以灵活地拟合变量之间的关系。进一步考虑了测量误差的存在,使得模型更加符合实际情形,可以更好地挖掘变量之间潜在的联系。模型的估计方法主要参考Cui等[10]和Huang[6]中的思想。
1 模型建立
含有扭曲测量误差的部分变系数单指标模型具有如下形式:
(2)
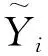
(1) ‖β0‖=1,其中‖·‖表示Euclid模;
(2)E|ψ(U)|=1,E|φr(U)|=1;
(3) 模型误差ε的方差是有限的。
其中,r=1,2…,p。假设条件(1)保证了单指标参数的唯一性,假设条件(2)保证了误差函数的可识别性,假设条件(3)保证了估计量的渐近性质。
接下来,介绍模型(2)的估计方法。首先估计误差函数,根据Cui等[10]和Delaigle等[11]中提出的方法,结合假设条件(2)可以得到:
因此可以用N-W核估计方法可以得到误差函数的估计式分别为
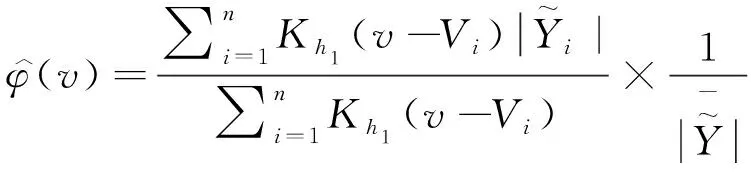
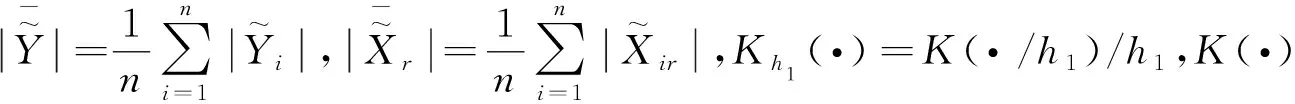
根据校正后的变量,可以得到模型(1)的一个近似形式
(3)
模型(3)的估计过程主要参考文献[6]中的思想和方法,简要表述过程如下:
令B={β∈Rp:‖β‖=1},可以推出β0∈B。由于假设条件(1)的存在,目标函数
β∈B,在β0处的一阶导数不存在,因此考虑使用Zhu和Xue[14]中的“去一分量”法得到β0的有效估计。不妨假设β的第r个分量βr>0,定义
β(r)=(β1,β2,…,βr-1,βr+1,…βp)T
则有
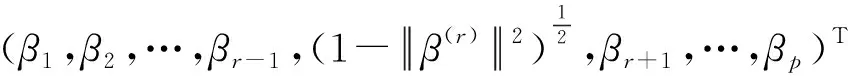
接着,可以计算出β关于β(r)的Jacobian矩阵为
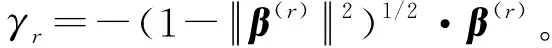
不难推出,{ηi(β(r)),i=1,2,…,n}是相互独立的且E(ηi(β(r)))=0。因此β(r)的经验对数似然比函数可以定义为
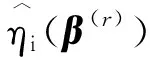
(4)
接下来,只要求解函数的初始估计值即可。对于函数的初始估计,考虑利用局部线性光滑方法分步求解系数函数和联系函数,具体的估计步骤如下:首先假设参数β0已知,对模型(3)的两边求条件期望,经过简单的计算可以得到:
其中
且有
参考Einmahl和Mason[15]的方法,应用N-W核估计求解两个二元函数的估计表达式。选择核函数K1(t,u)=K(t)·K(u)和带宽h2(n)→0,ωj(·,·)(j=1,2)的估计量分别为
接着,令a=(a1,…,aq)T和b=(b1,…,bq)T,在u的邻域内有
通过最小化加权平方和
可以得到系数函数θ(·)及其一阶导数θ′(·)的初始估计量为
其中κ(u)=diag(Kh2(U1-u),Kh2(U2-u),…,Kh2(Un-n))以及
然后,带入系数函数估计量到式(3)中,通过局部线性方法,类似地,可以得到联系函数g(·)及其一阶导数g′(·)的初始估计方程估计分别为
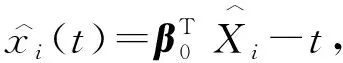
以及
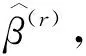
2 模型拟合
糖尿病数据集共包含442个样本观测值和11个变量,数据集来自Efron等[16]。Zhang等[17]利用含测量误差的部分线性单指标模型研究了该数据集,并且证明变量Sex和6种血清的化验数据与变量BMI可能存在非线性关系,受到该实验结果的启发,考虑用部分变系数单指标模型重新分析该数据集,观察变量Sex和6种血清的化验数据变量的系数是否受到BMI的影响。此外,考虑到病人的BMI可能与他的年龄和血压存在关系,因此假设变量Age和BP受到BMI的污染,具体的变量意义见表1。实验前,对各个变量进行了标准化处理。

表1 糖尿病数据集变量及其含义Table 1 The variables and meanings of diabetes data set
在非参数回归方法中,带宽对估计精度较大,因此使用合适的带宽选择方法十分重要。由于对于误差函数的估计方法比较简单,因此可以采用基于经验的拇指规则(Rule of Thumb)来选择带宽。选取h1=n-1/3SE(V),其中
而对于系数函数向量θ(·)和联系函数g(·)的估计比较复杂,因此使用交叉验证法(Cross-validation)选择最优带宽hcv,并令h2=hcv,h3=hcv(nlogn)-1/20。
根据第2节的模型估计方法,本次实验的具体算法流程如下:
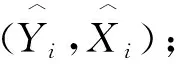
Step2 选择符合假设(1)的初始参数βini;
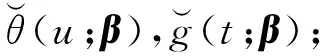
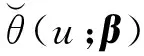
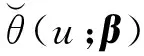
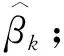
使用模型(2)对糖尿病数据集进行拟合,变量选择如表1所示。首先得到的是误差函数ψ(·)和φr(·)(r=1,2)的估计曲线,见图1和图2,其中图2(a)和图2(b)分别代表函数φ1(·)和φ2(·)的估计曲线。从估计曲线的趋势可以看出,各条估计曲线都不是水平的,这说明变量(Y,X1,X2)与混淆因子V存在非线性的关系,这验证了之前的实验假设:糖尿病患者定量测量数据,Age和BP受到了混淆因子BMI的污染。
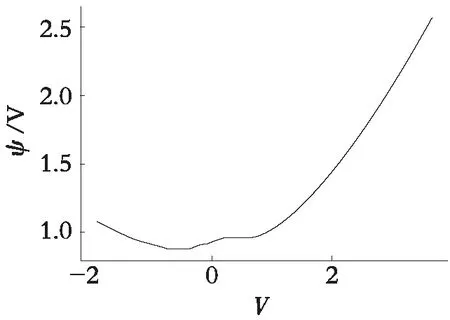
图1 ψ(·)的估计值Fig. 1 The estimation of ψ(·)
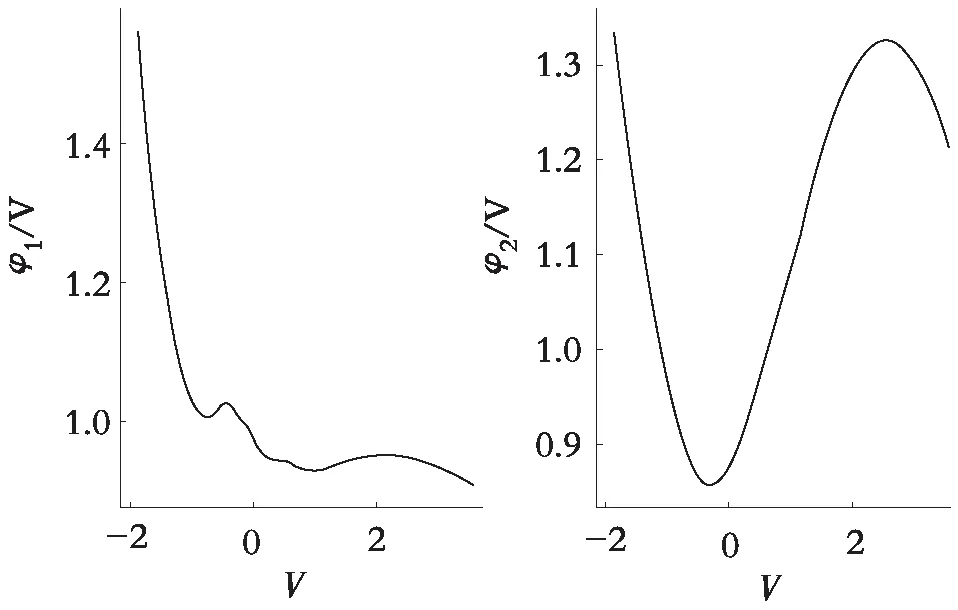
(a)φ1(·) (b)φ2(·)
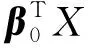
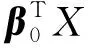
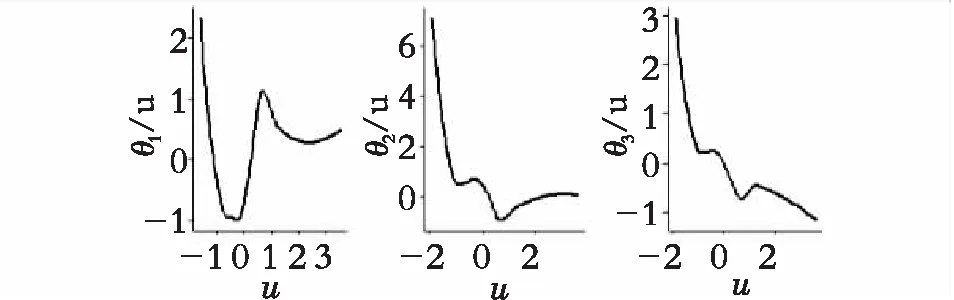
(a)Z1 (b)Z2 (c)Z3
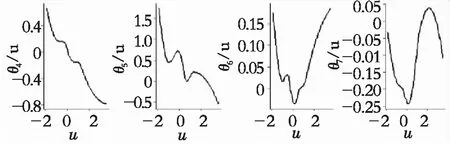
(d)Z4 (e)Z5 (f)Z6 (g)Z7
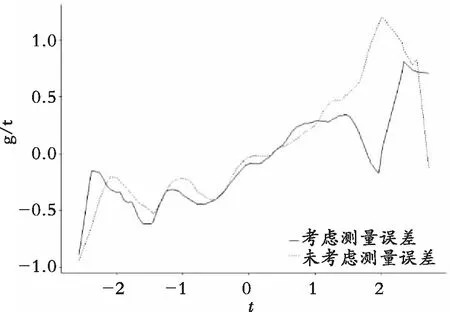
图4 联系函数g(·)的估计曲线Fig. 4 The estimation curve of contact function g(·)
3 结束语
对于高维数据分析,相较于传统的参数模型和非参数模型,半参数模型不仅可以较好地拟合数据,还可以避免“维数灾祸”问题,因此广泛地应用医药和经济等领域。此外,在实际应用中,由于外界因素的干扰,很难避免测量误差的产生,如果忽略误差的影响,就有可能导致模型拟合产生偏差,因此研究带有测量误差的模型应用问题是比较重要的。这里,针对糖尿病数据集,应用部分变系数单指标模型进行拟合,并假设变量Y和X受到混淆因子BMI的乘积污染。观察实验结果发现,6种血清测量数据和变量Sex的系数会随着BMI的变化而变化,并且对比带有测量误差和不含测量误差两种情形的结果发现,糖尿病人定量测量值、Age和BP均受到BMI的污染。这些结果说明选择单指标部分带有测量误差的部分变系数单指标模型对该数据集进行拟合是合理的,并且相较于不含测量误差的半参数模型,可以更好地挖掘数据中的信息。

