刚性折纸机构的运动学分析及其可折叠条件
张玉辉, 张 帆, 崔国华
(上海工程技术大学 机械与汽车工程学院,上海 201620)
0 引 言
折纸在生活中随处可见,它可以采用一系列较为复杂的过程将一个二维平面制成一个美丽的三维模型。1989 年,第一届折纸科学国际会议在意大利费拉拉城召开。1994 年,第二届折纸科学国际会议吸引了越来越多的研究学者参与,对于折纸的数理问题研究也越来越清晰,至此,一门新学科——折纸几何学诞生了,折纸数理也逐渐发展成为现代几何学的一个重要分支[1-4]。在以数理问题讨论的前提下,折纸总被理想化为无厚度。
随着近年来航空和建筑结构的发展,折纸进入了一些机构学专家的视线,并给予了他们新的灵感和启发。参考折叠机构,把折纸中的折痕类比为转动副[5],从而发展出了一系列的折纸机构。折纸机构具有折叠后占用空间小、便于携带运输、质量轻、展开后可以稳定保持等优点,这些优点正是吸引许多工程师关注的关键所在。常见的实例就是帐篷,它就具有典型的上述优点,所以也成为探险爱好者的必备。此外还有雨伞、英国牛津大学发明的折叠购物袋等[6]。更高层次的如能量吸收装置、太阳翼[7-8]、折纸医用支架[9]、生物医学中的微型折纸机器人[10-12]等。根据折叠过程中折痕之间的单元面是否发生形变,折纸机构又可分为柔性折纸机构和刚性折纸机构[13]。柔性折纸机构在折叠过程中单元面为柔性结构,可以发生变形,最常见的有雨伞、帐篷等。刚性折纸机构多了一种限制条件,即一系列的折叠运动是其单元面围绕预定折痕旋转,而它的单元面为刚性结构,不会发生扭曲变形。所以刚性折纸机构的单元面是一个分段线性的可展开平面,在机构学中可以用刚性平板和转动副分别代替单元面和折痕,折痕相交处顶点可以视为球面链接[14],这样就形成了一个机械结构。在工程项目中,这样的机械结构作用很大,例如在航空航天领域,构建一个空间的外表面密封结构,基于纯几何机制,不依赖于材料的弹性,可以重复使用且稳定。
目前,刚性折纸机构研究成果主要在刚性折叠和自由度分析等方面,霍夫曼(Huffman)[15]使用球面三角法分析了折纸机构二面角的关系;Balkcom等[16]推导了折痕转角的关系表达式;Belcastro[17]使用矩阵方法对论文进行建模,并讨论了刚性折纸的必要条件;Wu和You[18]利用四元数方法和双四元数方法,Nojima等[19]利用数值算法分析单顶点和多顶点折纸的刚性可折叠性;Chen等[20]采用D-H参数法在基于水雷结构的厚板化研究中分析了自由度;Cai等[21]使用雅可比矩阵分析了折纸机构的自由度;Chen等[22-24]使用非线性算法分析其运动特性并计算了机构的自由度;Yu等[25]利用螺旋理论分析单顶点和多顶点折纸机构的自由度;Tachi[26]提出了一种几何方法获得一维自由折叠的刚性折叠结构。以上研究均有效地推动了折纸机构理论的进步,但是由于折纸机构的多样性,许多分析方法都具有局限性,仅针对某些特定的构型,特别是在求解折痕转角关系的时候,采用的计算方法过于复杂,或得到的关系表达式较复杂,不够简明直观,有的没有考虑冗余解的问题,这些都限制了对于较为复杂折纸机构的理论研究。
总结上述这些问题,对刚性折纸机构折叠分析展开研究,核心是找到刚性约束,因为能折叠不代表一定能够刚性折叠。以三角形折纸机构为例,其中心三角形的3边,是连接3个单顶点折痕机构的公共转轴,若能刚性折叠,则作为公共转轴连接相邻顶点的两端必须协调一致,否则就会出现扭曲折叠。本论文从单顶点四折痕机构的运动学分析出发,找出单顶点折纸机构各折痕转角之间的关系,进而拓展到由单顶点四折痕机构组合而成的多边形折纸机构,找出其运动学关系,并围绕刚性折纸机构的公共折痕展开分析,推导出刚性折叠的判断依据。相对以往,简化了求解折痕转角关系的复杂计算过程,并进一步得到更加简明直观的转角关系表达式,对于不同的多边形折纸机构不需要再进行单独的运动学分析,扩大了适用范围,简化了较多繁琐且重复计算的步骤。
1 单顶点四折痕机构运动学分析
单顶点四折痕折纸机构是较为基础的折纸模型,对于复杂的多边形折纸机构运动学关系和折叠条件的研究都有重要的指导意义。图1所示为单顶点四折痕折纸机构折叠前后的状态,图中的α为相邻折痕间对应的扇形角,ψ为折叠时相邻扇面的二面角。对于单顶点四折痕折纸机构,假设了两种峰谷布置方式如图2所示。
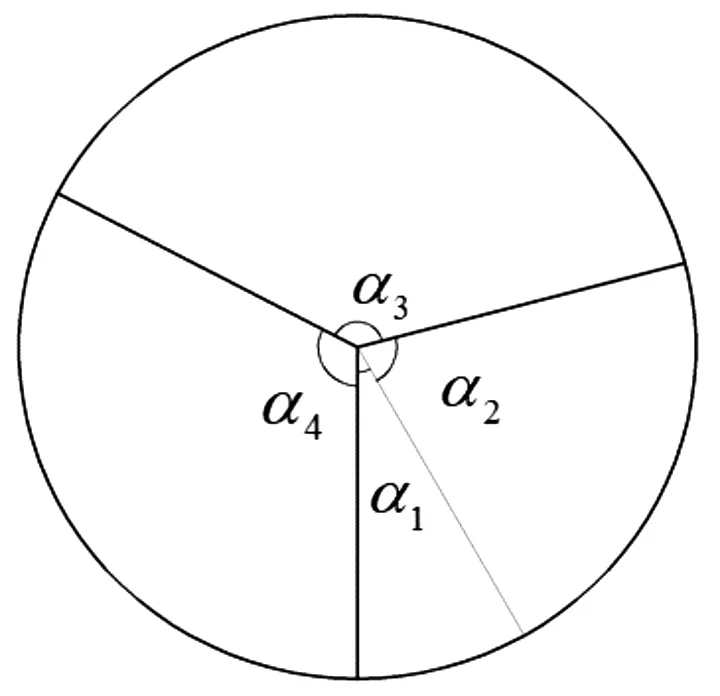
(a) 展开状态
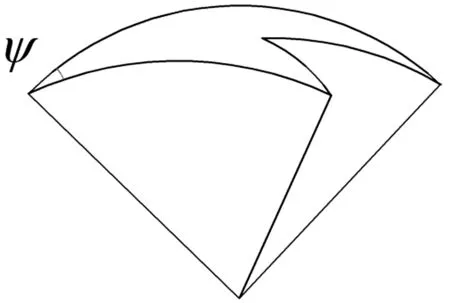
(b) 折叠状态
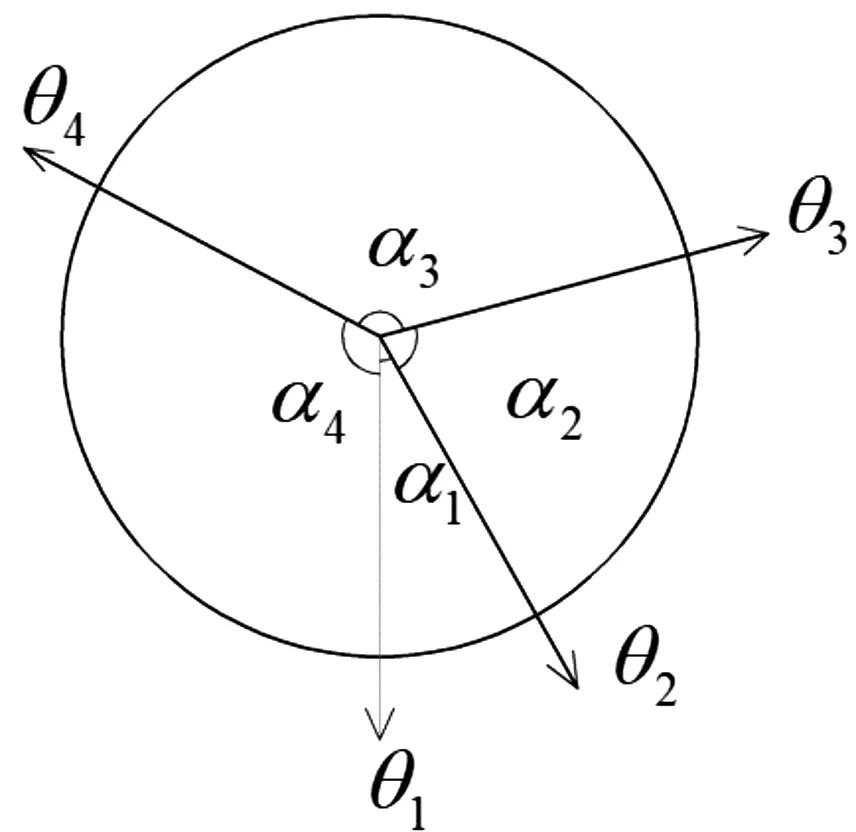
(a) Ⅰ型峰谷布置方式
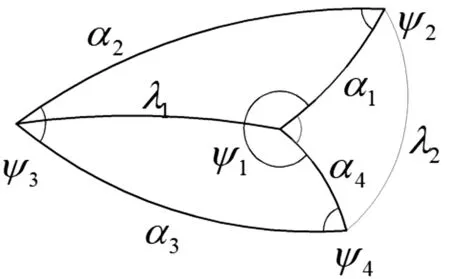
(b) Ⅰ型球面多边形
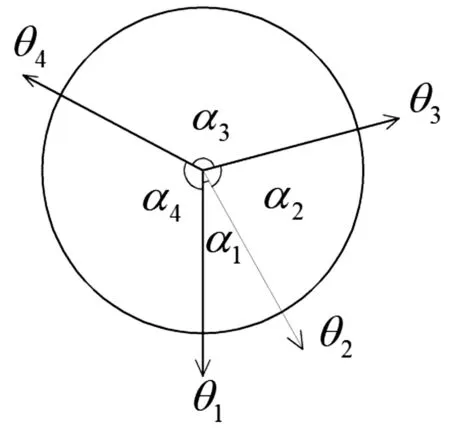
(c) Ⅱ型峰谷布置方式
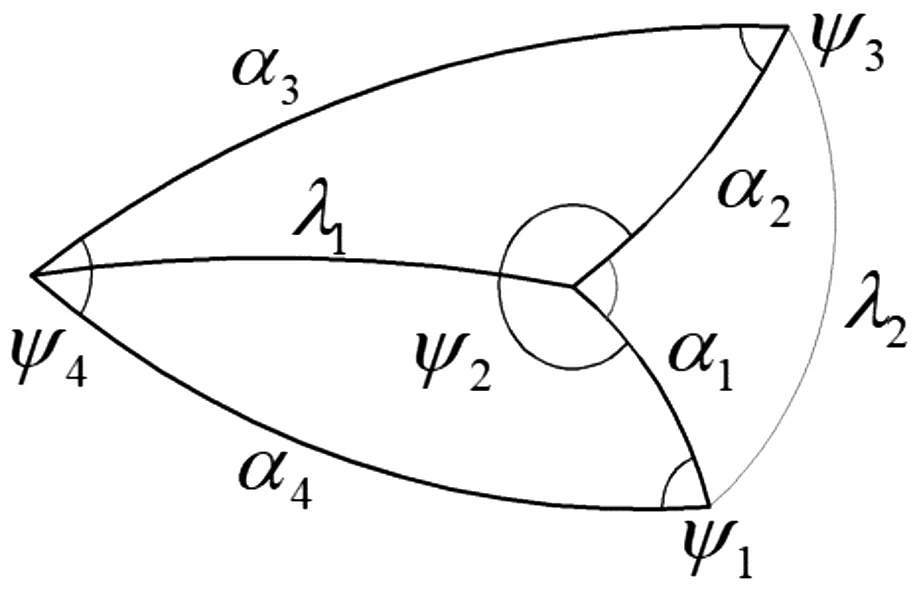
(d) Ⅱ型球面多边形
如图2(a)所示的Ⅰ型峰谷布置方式,θ1为谷折痕,经过折叠如图1(b)选取俯视图,可以得到图 2(b),同理,由图2(c)所示的Ⅱ型峰谷布置方式,θ2为谷折痕,可以得到图2(d);二面角ψ与折痕转角θ是互补的,对于峰折痕有ψ=π-θ,对于谷折痕有ψ=θ-π。
对于图2(b),令λ1为连接该多边形φ1和φ3角的球面上的弧,λ2为连接该多边形的ψ2和ψ4角的球面上的弧,将其分为4个球面三角形, 然后,依据球面三角学知识,如式(1)和式(2)所示:
cosλ1=cosα1cosα2+sinα1sinα2cosψ2
(1)
cosλ1=cosα3cosα4+sinα3sinα4cosψ4
(2)
对于单顶点四折痕折纸机构,根据川崎定理,可知扇形角关系如式(3)所示:
α3=π-α1,α4=π-α2
(3)
式(1)和(2)相减:
0=sinα1sinα2(cosψ2-cosψ4)
因为0<α1<π , 0<α2<π,所以cosψ2-cosψ4=0,而0≤ψ2≤π , 0≤ψ4≤π,得到:
ψ2=ψ4
(4)
同理:
cosλ2=cosα1cosα4+sinα1sinα4cos(2π-ψ1)
cosλ2=cosα2cosα3+sinα2sinα3cosψ3
得到:
2π-ψ1=ψ3
(5)
由式(4)和式(5)可以得到图2(a)折痕转角θ的关系如式(6)所示:
θ1=-θ3,θ2=θ4
(6)
同样,对于图2(d),令λ1为连接该多边形的ψ2和ψ4角的球面上的弧,λ2为连接该多边形的ψ1和ψ3角的球面上的弧,将其分为4个球面三角形,可得:
ψ1=ψ3,2π-ψ2=ψ4
图2(c)折痕转角θ的关系如式(7)所示:
θ1=θ3,θ2=-θ4
(7)
再根据Robert Lang推导得到的角度关系式,对于图2(b),有
结合式(1),式(4)和式(5),可得:
(8)
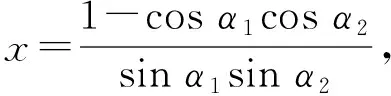
利用半角公式,如式(9)所示:
(9)
由二面角与折痕转角的关系,结合式(6),有
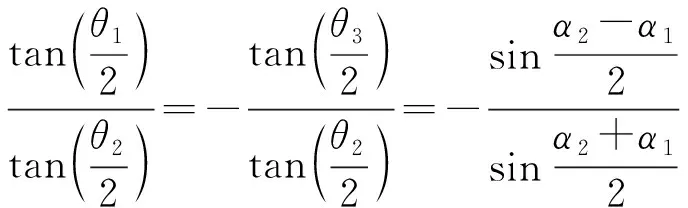
(10)
式(6)和式(10)表达了图2(a)单顶点四折痕机构的运动学关系。
同样对于图2(d),有
利用半角公式可得式(11):
(11)
由二面角与折痕转角的关系,结合式(7),有
(12)
式(7)和式(12)表达了图2(c)单顶点四折痕机构的运动学关系。
2 三角形折纸机构
由上面对单顶点四折痕机构的分析,可以进一步拓展到三角形折纸机构,如图3所示。
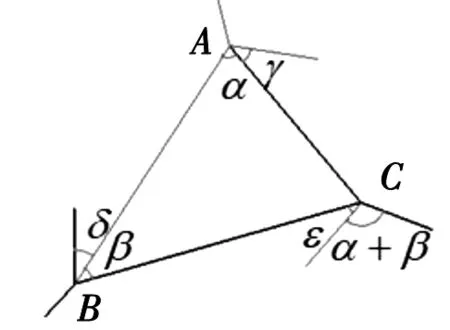
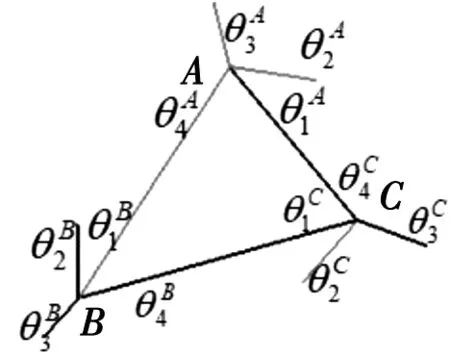
(a) 扇面角 (b) 折痕转角
2.1 运动学分析
对于三角形折纸机构,可以将其看作由3个单顶点四折痕机构组合而成,其顶点分别为A,B,C,它们都满足单顶点四折痕机构的运动学分析。
对于A顶点的四折痕机构,最小扇形角为γ,可以类比图2(a)的类型,如式(13)所示:
(13)
对于B顶点的四折痕机构,最小扇形角为δ,可以类比图2(a)的类型,如式(14)所示:
(14)
由刚性约束和单顶点四折痕机构的运动学关系,得到如式(15)所示:
(15)
结合式(13)和式(14),可得式(16):
(16)
总结三角形折纸机构的运动学关系如式(17)所示:
(17)
2.2 刚性可折叠条件
由前面的分析,对于A,B顶点的四折痕机构得到关系如式(18)和式(19)所示:
(18)
(19)
对于C顶点的四折痕机构,最小扇形角为ε,可以类比图2(c)的类型,如式(20)所示:
(20)
若要实现刚性折叠,则要满足刚性约束条件,如式(21)所示:
(21)
即有
(22)
当式(22)成立,则说明该三角形折纸机构可以实现刚性折叠。
对于图4折纸机构,A,B,C顶点的四折痕机构,根据式(10)和式(12),有
当kA>1,kB>1,kC<1时,给α,β,γ和δ分配任意值,根据刚性约束条件,如式(23)所示:
(23)
总是可以找到最小角ε满足上述条件,即图4第一类三角形折纸机构可以刚性折叠。
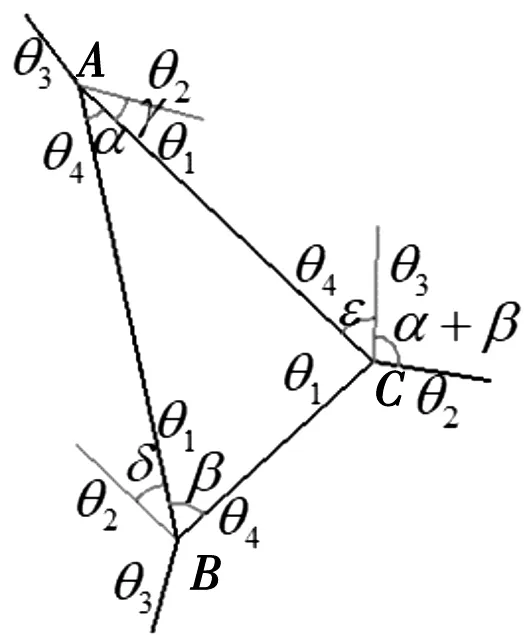
图4 第一类三角形折纸机构Fig. 4 The first type of triangular origami mechanism
对于图5折纸机构,A,B,C顶点的四折痕机构,根据式(10)和式(12),有
当kA>1,kB<-1,kC<-1时,根据刚性约束条件,如式(24)所示:
(24)
等式无法成立,即图5第二类三角形折纸机构不可以刚性折叠。
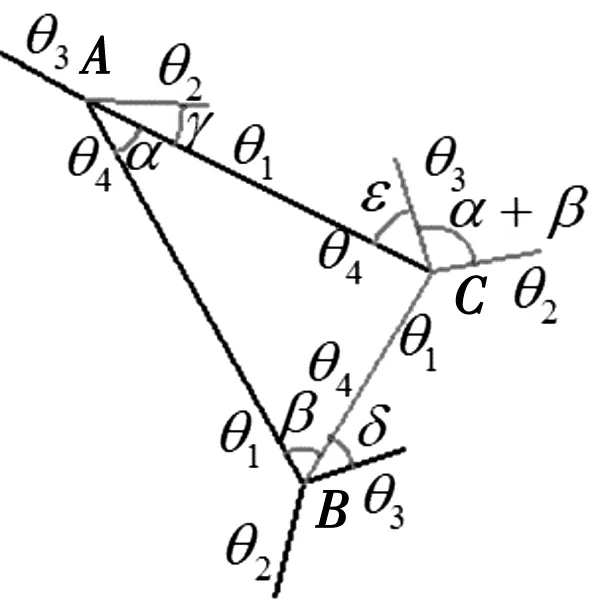
图5 第二类三角形折纸机构Fig. 5 The second type of triangular origami mechanism
3 四边形折纸机构的分析
3.1 运动学分析
如图6所示的四边形折纸机构,按照前面三角形折纸机构的分析思路,可以将其看作由4个单顶点四折痕机构组合而成,其顶点分别为A,B,C,D,它们都满足单顶点四折痕机构的运动学分析。
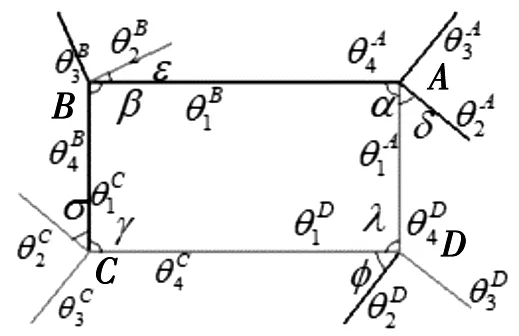
图6 四边形折纸机构Fig. 6 Quadrilateral paper folding mechanism
对于A顶点的四折痕机构,最小扇形角为δ,可以类比图2(a)的类型,关系如式(25)所示:
(25)
对于B顶点的四折痕机构,最小扇形角为ε,可以类比图2(c)的类型,关系如式(26)所示:
(26)
对于C顶点的四折痕机构,最小扇形角为σ,可以类比图2(a)的类型,关系如式(27)所示:
(27)
由刚性约束和单顶点四折痕机构的运动学特性,可以推出折痕转角关系如式(28)所示:
(28)
再结合式(25),(26)和(27),有
(29)
通过式(28)和(29),得到了四边形折纸机构的折痕运动学关系。
3.2 刚性可折叠条件
由前面的分析,对于A,B,C,D顶点的四折痕机构可以得到关系如式(30)所示:
(30)
同理,若要实现刚性折叠,则要满足刚性条件,如式(31)所示:
(31)
也即
(32)
所以满足式(32)即可实现刚性折叠。
4 结 论
主要研究了折纸机构的运动学关系并对刚性折叠条件进行了推导,以单顶点四折痕折纸机构为基础,对两种不同峰谷分配方案的运动学关系进行了具体分析推理,进一步拓展到多边形折纸机构。对于多边形折纸机构,其中心的多边形可以视为公共转轴,若作为公共转轴,两端转动角度能够保持一致,则判断可实现刚性折叠,否则就不能刚性折叠,所以关键是分析刚性折纸机构的运动特性。因此,可将多边形折纸机构拆分为若干个单顶点四折痕折纸机构,运用球面几何学、三角函数等数理方法进行分析,其中以三角形折纸机构和四边形折纸机构为例分析了折痕转角的运动学关系和刚性折叠的成立约束条件,通过对较为简单基础的折纸模型的特性分析,结合刚性约束这一条件,拓展到更为复杂的多边形折纸机构,简化以往对不同折纸机构需要单独进行分析研究的复杂过程,扩大了适用范围,避免了较多重复的计算推导,对于研究判断更为复杂的多边形折纸机构能否刚性折叠提供了通用化的判断依据。

