中频直流点焊机恒流控制方法研究与仿真

李玉鑫， 王 宾

(安徽理工大学 电气与信息工程学院,安徽 淮南 232000)

0 引 言

电阻点焊是利用大电流通过处在电极压力作用下的被焊工件，在短时间内产生大量的焦耳热，使焊件之间的接触点熔化后形成焊点，从而将它们焊接起来。电阻点焊具备的优点是：生产效益高、成本低、易于实现自动化，如今被广泛应用于材料、医疗、电气设备、机械制造等场合。PI控制作为一种经典的控制方法，因其具有良好的控制性能，被广泛应用于工业控制的诸多场合。而对于点焊机系统而言，负载电阻随时间非线性变化、变压器线圈之间存在耦合，这些因素导致无法对系统建立精确的数学模型。因此，仅采用PI控制满足不了实际焊接的需求。

近些年，人工智能技术的发展较为迅速，大量的智能算法不断涌现，模糊控制就是其中之一，它的典型特征是可以灵活地应用于没有精确数学模型的系统中。文献[1]设计了模糊积分控制算法对点焊机的输出电流进行控制，引入积分环节在很大程度上减小了焊接电流的稳态误差，改善了系统的动态性能。文献[2]提出了基于模糊神经网络的PID算法，利用模糊神经网络对PID 3个参数进行在线整定，提高了系统的鲁棒性。文献[3]通过设计系统的硬件电路和软件算法，准确产生PWM信号，实现了对焊接电流的恒峰值控制，确保焊接电流的对称性。文献[4]为了减小逆变器开关管的功率损耗，对全桥ZVZCS逆变主电路进行仿真，实现了超前桥臂的ZVS和滞后桥臂的ZCS。文献[5]从减小变压器一次侧电流尖峰和磁饱和的角度，提出了超前磁滞控制，使焊接电流在最大值和最小值之间变动，并且控制磁通也在一定的范围内，从而避免了一次侧电流尖峰的产生。但是上述方法中，没有考虑焊接过程中负载电阻变化的情况，并且操作复杂，电路设计成本高。

为了提高焊接电流的稳定性，设计了模糊控制与PI控制二者相结合的控制算法。当负载电阻变化时，模糊控制器可以对PI参数实时进行在线整定，从而实现系统的恒电流输出。与PI控制相比，模糊PI控制的输出电流超调小、调节速度快、系统鲁棒性好。

1 系统结构组成与设计

1.1 系统结构

中频直流点焊机系统的结构如图1所示，它包括了由三相桥式整流电路、滤波电路、全桥逆变电路、中频变压器、次级单相全波整流电路以及负载电路组成的主电路和32位TMS320F28335 DSP数字控制器、PWM驱动电路、外部输入电路以及电流采样电路构成的控制电路。其中，DSP的输入信号是焊接电流的采样值和设定值，二者的偏差经过一系列的运算处理后，输出使逆变器工作的驱动信号。

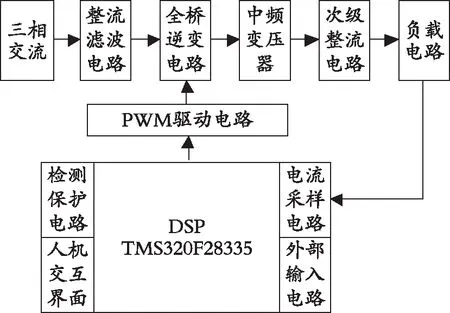
图1 中频直流点焊机系统结构框图Fig. 1 System structure block diagram of medium frequency DC spot welding machine

逆变电路是主电路设计的核心，逆变器的结构通常有以下3种：单端双管正激式、半桥式和全桥式。单端双管正激式的结构比较简单，不会出现因为电路不对称而带来的变压器偏磁现象，这样就有效地避免了一次侧电流尖峰的产生，但是它对变压器铁芯的利用率不高，只有半桥和全桥的一半。半桥逆变器和全桥逆变器在结构上的区别在于，前者由两个开关管构成，只有一个桥臂。因此，在直流侧电压相同的前提下，其输出电压幅值只有全桥的一半，大多用在几千瓦以下的小功率场合。另外，全桥逆变器的一个显著优点是，它能工作在双向激励的模式下，在很大程度上减小了中频变压器的体积，从而缩小了点焊机的体积。通过以上比较，选用全桥逆变器作为点焊机系统的逆变电源，如图2所示。其中，全桥逆变器由4个IGBT开关管V1～V4和各自反并联续流二极管VD1～VD4构成，其功能是将直流电压Ud逆变成频率为1kHz的交流方波信号，之后经变压器T降压和VD5、VD6整流，给负载电阻R提供直流电。

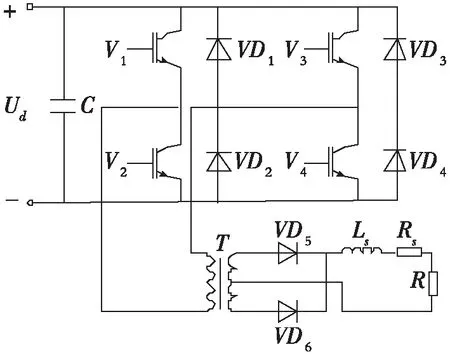
图2 逆变主电路Fig. 2 Inverter main circuit

为了减小逆变器开关器件的功率损耗，PWM波的生成方式采用移相法，如图3所示。4路PWM波的占空比都为0.5，在导通时间上，V1和V2相差半个周期，V3和V4相差半个周期，而上桥臂的两个开关管V1和V3的相位相差θ角，θ也就是模糊PI控制器的输出。另外，为了避免同一桥臂的开关管同时导通而导致电路短路，烧坏器件，必须要设置一定的死区时间β。

1.2 负载电阻曲线

焊接开始前，电极以预定的压力压在工件的对侧，如图4所示，负载电阻可表示为

R=Rr+R2+R3+R4+R5

(1)

其中，R1、R5分别是上下电极的电阻，R2、R4是电极与工件的接触电阻，R3是上下工件的电阻之和。

航空服务人员需要做好服务，就要将旅客视为家人进行服务，去倾听旅客的诉求。在倾听的过程当中，需要时刻保持自身姿势，并且伴随微笑和认同地点头。只有这样，才可以让旅客感受到服务人员在用心地倾听。只有服务人员了解旅客的真实想法后，才更好地理解对方，并降低矛盾出现的概率，让服务工作顺利地开展下去。当对旅客需求进行了解后，服务人员需要站在旅客的角度来处理问题，用关怀来去感动旅客，尽可能地满足旅客，让他们有个舒心的旅程。

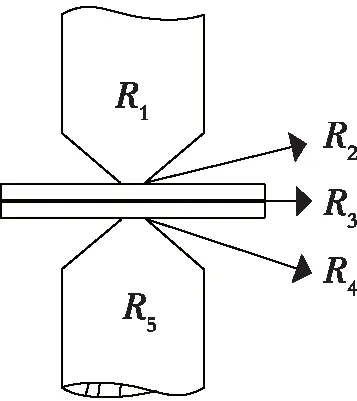
图4 电阻点焊示意图Fig. 4 Schematic diagram of resistance spot welding

在焊接过程中，负载电阻是随时间非线性变化的，其变化趋势与焊接工件的材料有关。为了更直观地观察负载电阻的变化情况，选用高温合金材料进行焊接实验，经过多次试验，拟合出图5所示的电阻曲线。可以看出，焊接开始时，负载电阻很大；一段时间后，随着焊接温度的升高，负载电阻迅速减小；同时焊核体积也在不断增大，限制了动态电阻的变化，使得R最终趋于稳定。

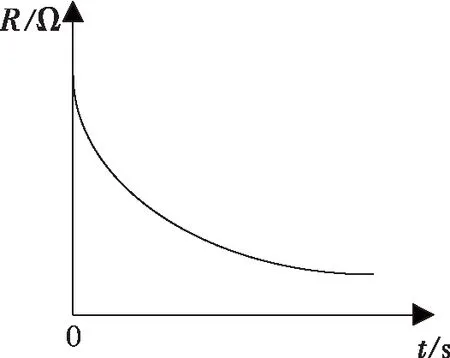
图5 高温合金的电阻变化曲线Fig. 5 Resistance curve of superalloy

1.3 模糊PI控制器的设计

对于点焊机系统而言，焊接电流是反映焊接质量的重要指标之一。由于一维的模糊控制器的输入仅仅是电流的偏差，很难反映焊接电流的动态特性品质，而三维的模糊控制器的运算过程太过于复杂，实际中用得较少。因此，结合对系统的实际控制需求，设计中采用两输入两输出的模糊控制器，其输入是焊接电流设定值I*与实际输出电流I的差值Ie以及差值的微分dIe/dt，输出是比例系数和积分系数的整定值△kp和△ki，原理图如图6所示，则修正后的PI控制器参数可用式(2)表示。在焊接过程中，当负载电阻改变时，用修正后的参数对焊接电流进行控制，从而确保输出电流能稳定在给定值附近，这样在很大程度上提高了焊接质量。

Kp=P0+Δkp
Ki=I0+Δki

(2)

其中，P0、I0是PI控制器的初始比例系数和积分系数；Δkp、Δki是比例系数和积分系数的修正值。

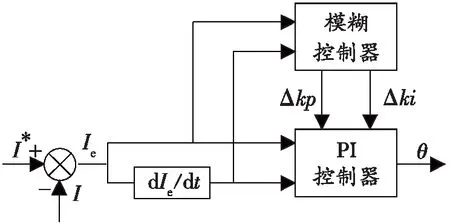
图6 PI控制器参数的整定原理图Fig. 6 Schematic diagram of parameter setting of PI controller

式(2)中，P0和I0的确定至关重要，它们相当于控制焊接电流的大信号，对整个系统的影响较大，而△kp和△ki只相当于小信号，小信号通过对大信号进行一定范围内的调整，使系统达到更好的性能。

1.3.1P0和I0的确定

在Matlab中搭建点焊机系统基于常规PI控制的电流闭环模型，设置给定电流为最大电流(10 kA)的70%(7 kA)。第一步，在纯比例控制的情况下，确定比例系数P。从0开始逐渐加大P,直到焊接电流出现振荡；再将此时的P值反向减小，直至振荡消失，设定P0为当前值的65%。确定积分系数I的方法与上述方法类似，区别在于，I不是从0开始增加，而是先设定一个较大的I，在输出电流不振荡的情况下，逐渐减小I；一旦系统振荡，则将此时的I值反向加大,直到振荡消失，设置I0为当前值的1.6倍。通过不断调节，最终确定P0=0.6，I0=7。

1.3.2 模糊控制器的设计

图7中，E、EC表示电流误差和误差变化率的模糊量，Kp、Ki是比例系数和积分系数修正值的模糊量，Ke、Kec分别是E、EC的量化因子，Gp、Gi分别是△kp、△ki的比例因子。

图7 二维模糊控制器Fig. 7 Two dimensional fuzzy controller

在实际焊接过程中，由于焊接电流的偏差Ie和偏差变化率dIe/dt会随着负载电阻的变化而变化。此时，为了使E和EC的模糊论域保持不变，可以通过调节量化因子Ke和Kec，即可以将变化后的Ie和dIe/dt映射到开始设置的模糊论域中。因此，E和EC的模糊论域选择没有具体的要求，这里都设置为[-3,3]。同理，Kp、Ki经清晰化以后，通过调节比例因子Gp、Gi，就可以得到物理论域中比例系数和积分系数的修正量，这里选取Kp、Ki的模糊论域均为[-6,6]。

假设模糊控制器输入量的实际变化范围是[a,b]，其对应的模糊论域为[-N,N]；输出量的物理论域是[c,d]，其对应的模糊论域是[-M,M]。

则该输入量的量化因子可表示为

(3)

输出量的比例因子表达式为

(4)

根据式(3)可求得量化因子初值Ke=6/420=0.014、Kec=6/21=0.286，根据式(4)可求得比例因子初值Gp=0.108/12=0.005、Gi=1.26/12=0.105。仿真时还需要对这些参数不断修改，以确定最优参数。

为了使任意时刻输入的Ie和dIe/dt都能被模糊化，在覆盖E和EC的模糊论域[-3,3]上用7个模糊子集：负大(NB)、负中(NM)、负小(NS)、零(Z)、正小(PS)、正中(PM)、正大(PB)来表示。根据系统的特点并结合隶属函数的性质，输入量和输出量的模糊论域左边界、中间、右边界的模糊子集隶属函数，分别选取zmf型、trimf型和smf型，隶属函数分布曲线如图8所示。

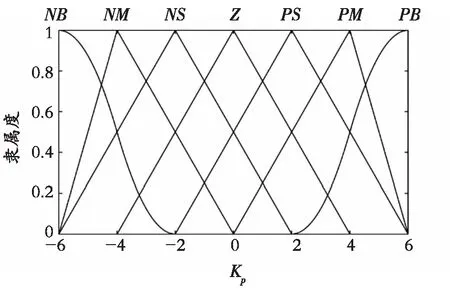
(b) Kp的隶属函数分布

模糊逻辑推理的结果是输出量的模糊集合，需要把它等效成一个清晰值并经过比例变换后，才能得到控制PWM移相角的实际量，这里采用centroid清晰化方法。

归纳总结对点焊机系统的实际操作经验，寻找Kp、Ki与E、EC之间的模糊关系，进而建立合适的模糊控制规则表，是设计模糊控制器的核心。在建立控制规则时，应该以Kp、Ki对系统的调节作用和消除E、EC的主次性为原则：当误差E较大时，此时应以消除误差为主，因此，取较大的Kp，快速减小误差。但是Kp的取值不能太大，这样会导致焊接电流产生超调和振荡。当E和EC适中时，此时应适当减小Kp，并取适当的Ki，同时兼顾E和EC的变化。当E较小时，为了尽可能减小焊接电流的稳态误差，在电流稳定的前提下，此时要适当增加Ki。基于以上的控制规律并结合实际输出电流的波形特点，总结出了Kp和Ki的模糊控制规则，分别如表1和表2所示。

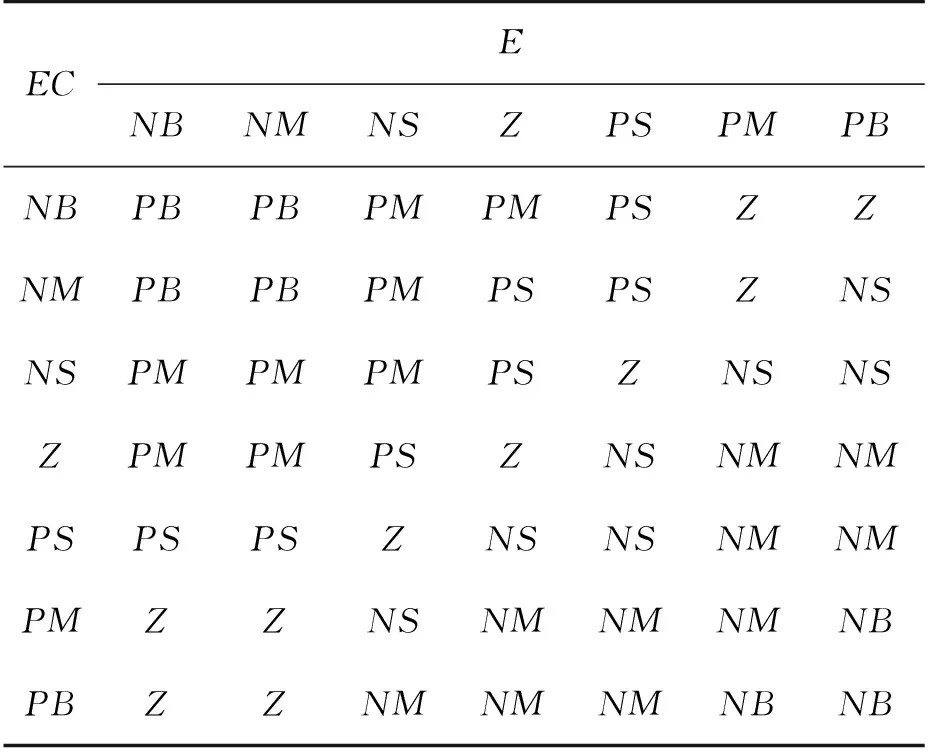
表1 Kp的控制规则表Table 1 Control rules of Kp

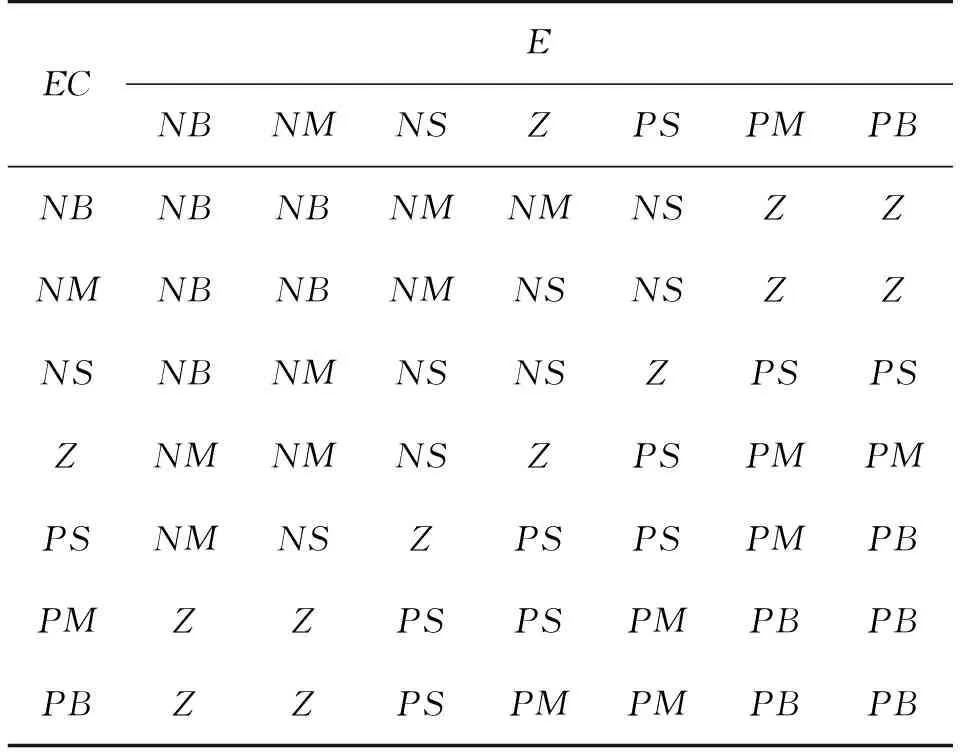
表2 Ki的控制规则表Table 2 Control rules of Ki

2 系统仿真与结果分析

为了验证所得结论的正确性，利用仿真软件Matlab/Simulink搭建了中频直流点焊机系统的仿真模型，电路的参数设置见表3所示。

2.1 搭建仿真模型

图9是基于模糊自适应PI控制的系统仿真模型，其中，上半部分是主电路，下半部分是控制电路。仿真时间设为0.2 s。在焊接过程中，为了模拟负载电阻变化对焊接电流的影响，在0.1 s时，通过Breaker模块接入电阻R1，使其与R并联，即可以使负载电阻减小。

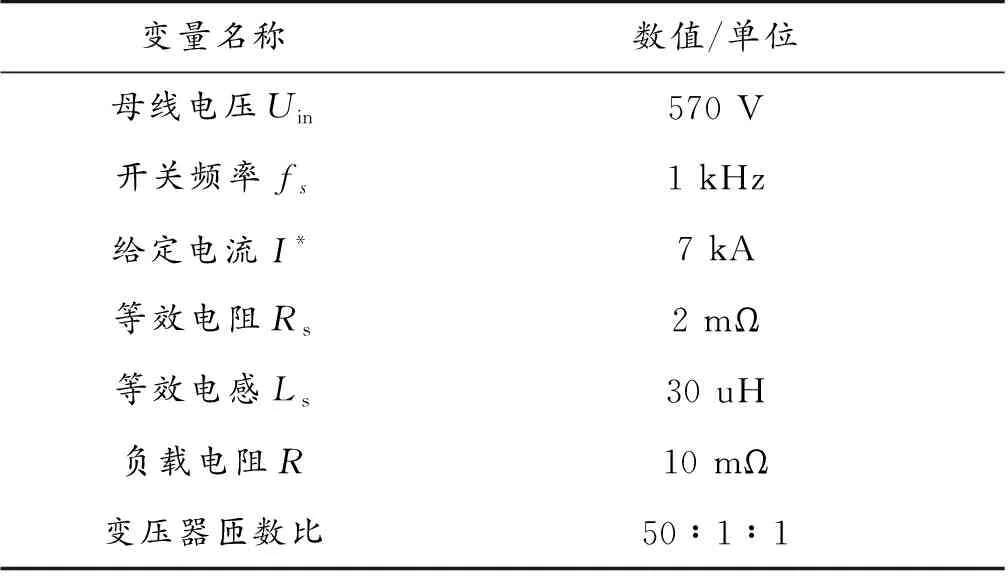
表3 仿真参数Table 3 Simulation parameters

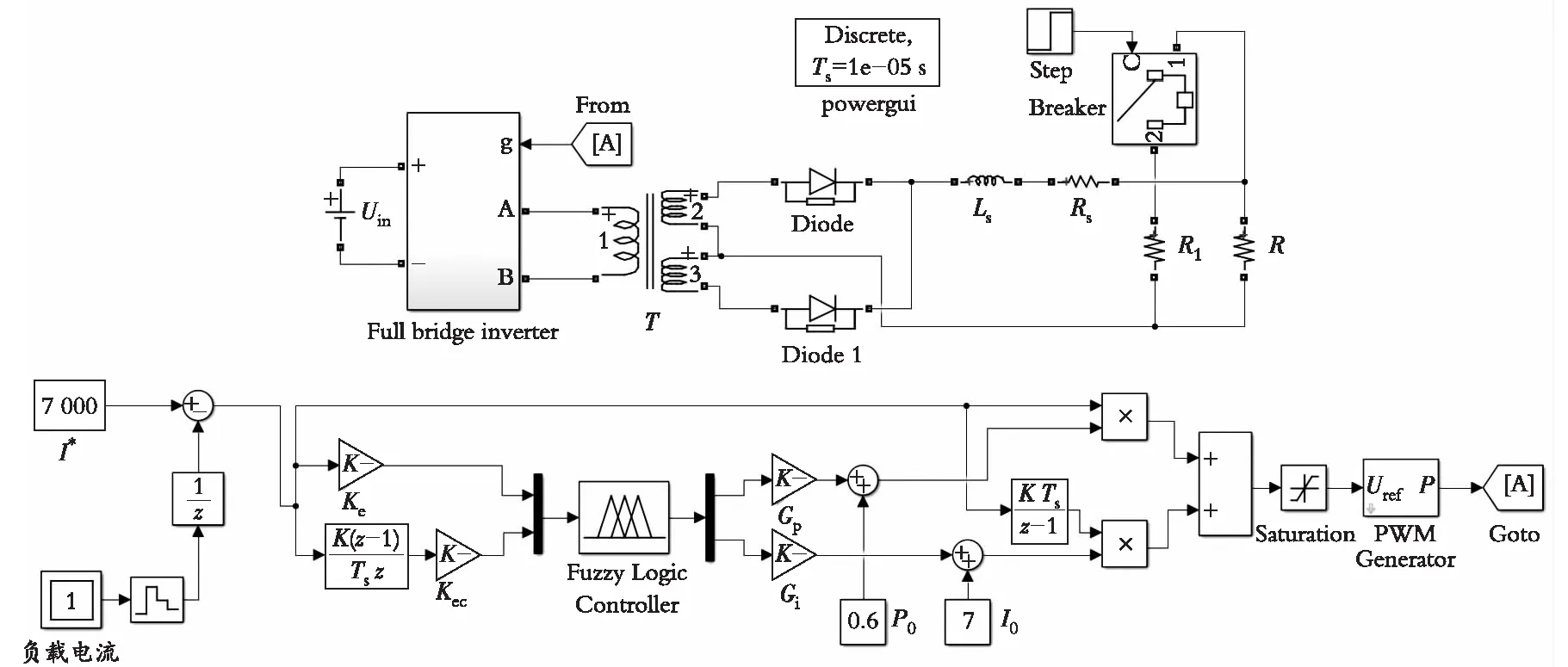
图9 系统仿真模型Fig. 9 System simulation model

2.2 结果分析

设置给定的焊接电流为7 kA，图10是焊接电流在上升阶段的波形。可以看出，在稳态之前，PI控制的电流波形发生了振荡和超调，最大超调量约400 A，上升速度较模糊PI控制缓慢，波形在0.06 s时才稳定。而模糊PI控制的电流波形很平滑，几乎没有超调，0.025 s就达到稳态，系统的响应速度得到了明显提升。

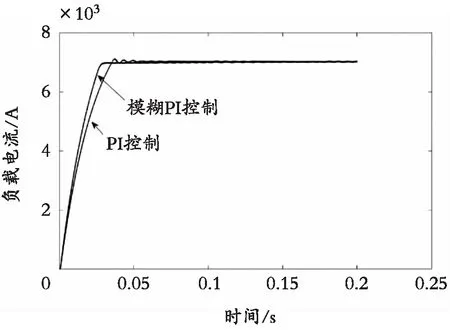
图10 负载电流上升阶段波形Fig. 10 Waveform of load current rising stage

在0.1 s时，负载电阻发生突减。图11是负载电阻变化时，两种控制方法下的焊接电流波形。可以看出，在开始的一段时间内，PI控制的负载电流在6 800 A～7 200 A波动，之后波动范围逐渐减小。而模糊PI控制的电流始终没有发生振荡，只是在电阻突变后的5 ms内，电流略微增加，但是很快就调节至电流给定，提高了系统的鲁棒性。

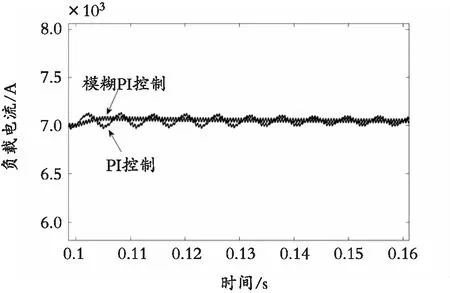
图11 负载电阻变化时负载电流波形Fig. 11 Load current waveform when load resistance changes

3 结束语

针对电阻点焊过程的非线性、强耦合等特点，设计了一种基于模糊PI的中频直流点焊机恒流控制方法。利用模糊控制器对PI控制器的比例系数和积分系数进行在线修正，从而使系统获得比常规PI控制时更好的动态性能。为了验证结论的正确性,对两种控制方法作用下的系统进行Simulink建模仿真。仿真结果表明，模糊PI控制相对于常规PI控制而言，在电流上升阶段，其输出电流超调小、波形平稳、调节速度快；当负载电阻变化时，其输出电流波动小、恢复到给定的时间短、抗扰动能力强。