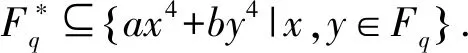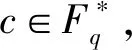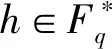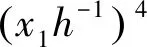有限域上四次对角方程ax4+by4=c解的存在性

黄宝盛, 吴荣军, 谭千蓉, 朱光艳

(1. 四川大学数学学院， 成都 610064； 2. 西南民族大学数学学院， 成都 610041；3. 攀枝花学院数学与计算机学院， 攀枝花 617000； 4. 湖北民族大学教育学院， 恩施 445000)

1 引 言

有限域上方程解的存在性以及解的个数[1-16]一直是数学家们十分关心的问题.关于这一问题的第一个重要的结果是Lagrange[4]给出的: 有限域Fp(p为素数)上的n(n≥0)次单变量多项式至多只有n个根.这结论在一般的有限域Fq(q为素数方幂)上也成立[5].如下问题直接推动了有限域理论的发展.

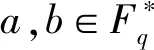
axd+byd=c

在有限域Fq上是否恒有解？

当a=b=1,d=2时,答案是肯定的.这就是有限域中熟知的结论[11]:Fq中的元素都可以写成两个元素的平方和;当a=b=1时,对一般的d,Small[10]给出了问题的肯定回答并确定了q的下界.设d为正整数,Fq为q元有限域,记δ=gcd(d,q-1).若q>(δ-1)4,则Fq中任意元素均可写成该域上的两个d次方幂之和.

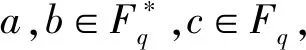
2 预备知识

在本节中，我们定义一些记号并给出几个引理.

定义2.1设p为素数,k为正整数.令q=pk.记Fq为q元有限域.对任意Fq的子集A,我们定义A在Fq上的概率测度为μq(A)=|A|/q,其中|A|为集合A中元素的个数.

定义2.2设A⊂Fq,记1A为集合A的特征函数,对任意的x∈Fq,定义

定义2.3设f1,f2是定义在Fq上的两个复值函数,定义它们的内积为

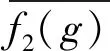
|〈f1,f2〉|≤‖f1‖·‖f2‖.

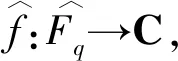
类似地，对任意的a∈Fq，我们可以给出Fourier反演公式如下：

引理2.7[1]设d为正整数,q为素数方幂, 若δ=gcd(d,q-1), 则

{xδ|x∈Fq}={xd|x∈Fq}.

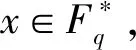
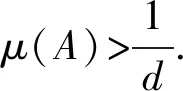
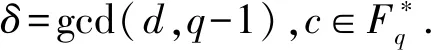
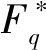
那么对任意i∈1,…,q-1有Tχ1(gi)为方程

的根, 其中s由如下条件唯一确定:

q=s2+4t2,q≡1(mod 4)

并且如果p≡1(mod 4),那么gcd(s,p)=1.

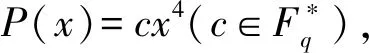
μ(Aq)μ(Bq)|≤κ(q).

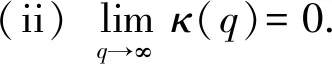
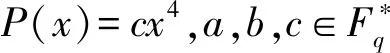
证明 为简便起见,记A=Aq,B=Bq,μ(A)=μq(A).对任意的g,h∈Fq，由定义2.1和2.2可得

1A∩B(g)=1A(g)1B(g),

1A+g(h)=1A(h-g).

因而

由Fourier反演公式可得

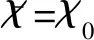
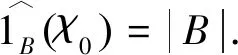
μ(A)μ(B)+

进而有

μ(Aq)μ(Bq)|=

接下来我们对

的上界进行估计.不妨记该上界为κ(q).由三角不等式,我们有

(1)

因

q2〈1A,1A〉=q2μ(A)，

由Cauchy-Schwarz不等式有

(q4μ(A)μ(B))1/2≤

(2)

把式(2)代入式(1)可得

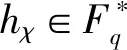
χ(P(g))=χ1(hχP(g))=χ1(hχcg4).

对g∈Fq求和,由引理2.9我们有

于是,当q≡5(mod 8)时,对任意Fq上的加法特征χ,指数和∑g∈Fqχ(P(g))为方程

x4+2qx2+8qsx+9q2-4qs2=0

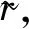
(3)

(4)

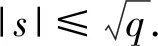
2r2q2+8rq2+9q2=(2r2+8r+9)q2

(5)

可以解得，当r>2.55254时,2r2+8r+9

因而我们可以取

这样我们就完成了引理的证明.

(i) 当b=0时,

(ii) 当b≠0 时,

τ(j)=|{1≤i≤s∣(ai)n=(αj)n}|,

3 主要定理的证明

情形1p=2.我们有

gcd(4,q-1)=gcd(4,2k-1)=1.

其中 |ε|=1,θ(b)≥0,τ(j)≤2.简单放缩有

令N>0,解得q≥342.因而,当q=32t,t≥4 时,恒有q>342，即该方程在Fq上有解.经检验,当q=81和729时,该方程在Fq上也有解.综上,当q=32t,t≥2 时方程ax4+by4=c在Fq上恒有解.

情形3p≥5.若q≡3(mod 4), 则有gcd (4,q-1)=2.与情形2的讨论类似知方程ax4+by4=c在Fq上也有解.若q≡1(mod 4),我们分q≡1(mod 8)与q≡5(mod 8)两种情况讨论.

令算术函数

(6)

即断言成立.

若q≡1(mod 8),同理可得q>2335时不等式(6)成立.下面我们分别定义

由引理2.10和2.11可知

S-μ(Aq)μ(Bq)≥-κ(q)

成立.因此

(S-μ(Aq)μ(Bq))+

-κ(q)+κ(q)=0.

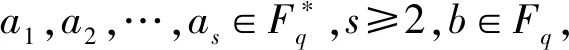
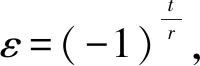
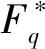
综上,我们证明了当q≡1(mod 8)且q>2335以及q≡5(mod 8)且q>139时,Fq⊆{ax4+by4|x,y∈Fq}.其他情形可借助Magma直接验证知若q≠5,9,13,17,25,29,方程ax4+by4=c在Fq上恒有解.至此,我们完整地给出了定理的证明.