周期多孔结构的Steklov弹性特征值问题的多尺度渐近分析

谭理琴， 马 强， 胡 兵

(四川大学数学学院， 成都 610064)

1 引 言

多孔材料在现代工程中应用非常广泛.多孔材料微观结构的自由振动行为的预测在数学上可以归结为一个求解弹性特征值方程的初边值问题.该问题通常只能进行数值计算. 对于这类高度非均匀材料，传统的数值方法需要产生精细的计算网格才能准确捕捉结构的微观特征，计算量大. 为有效减少计算规模，国内外学者们采用多尺度方法来对结构的微观构型与宏观性能之间的关系展开研究[1-3]. 1964年，Marchenko和Khruslov[4]首次提出了多尺度渐近展开法，并针对各类数学物理问题建立了多尺度渐近表达式[5]. 之后，Hou和Wu提出了多尺度有限元方法[6]，并展开了实际计算. 崔和曹[7, 8]引入了复合材料物理力学行为的二阶双尺度(Second-Order Two-Scale, SOTS)渐近展开方法[6-8]，可以更准确捕捉结构的局部微观振荡行为.

本文采用二阶双尺度渐近展开方法研究周期多孔结构中的Steklov弹性特征值问题. 以往的研究主要讨论了周期性椭圆特征值问题的均匀化方法[9，10]，如Vanninathan[11]给出了在周期孔洞区域上Dirichlet和Steklov以及Neumann三种孔洞边界条件下的特征值问题，其中的结果都未曾考虑到对特征函数与特征值进行二阶双尺度分析. 我们以往的工作[12]表明二阶双尺度渐近展开式对于有效给出结构特征值与特征函数的近似解是必不可少的.本文讨论Stkelov弹性特征值问题的二阶双尺度渐近分析方法，给出结构特征值与特征函数二阶展开式，并建立有限元计算方法，最后通过数值算例验证了多尺度模型有效性.

2 多孔结构Steklov特征值问题

考虑图1所示的周期孔洞区域Ωε(图1(a))和单胞区域Q*(图1(b)). 将孔洞填满, 我们可得到一个单连通有界区域Ω⊂RN，其中N表示维度(N=2,3)，边界∂Ω满足Lipschitz条件. 孔洞定义为ωε，Ωε可表示为Ωε=Ω-ωε. Ωε对应的参考单胞为Q*=Q-ω，其中Q=[0,1]N，ω⊂Q为有界开集. 这样, Ωε由单胞Q*以周期ε沿坐标轴排开而形成，即

(a) 位移变形图(a) Deformation graph

(a) Ωε

其中I是指标集，表示为

I={z∈Zn|ε(Q*+z)⊂Ωε}.

可以看到，ε为结构宏观尺度与微观尺度的比值.同样得到

此外，假定ω的边界为S且不与外边界∂Q相交，得到

∂Q*=∂Q∪S,

基于以上设置，考虑如下周期孔洞区域上的Steklov弹性特征值问题：

(1)

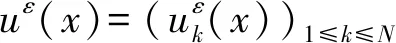
ξ=(ξi∈RN,0≤ρ0<ρε(x)≤M，

这里β1,β2和M是正常数. 由结构的周期性, 这些材料系数可表示为

其中cijkl(y),ρ(y)是关于y的周期函数.∂Ω由齐次Dirichlet(Γ1)和Neumann(Γ2)构成，且有∂Ω=Γ1∪Γ2,Γ1∩Γ2=∅.

上述特征值问题对应的变分形式为: 求(λε,uε)，使得

a(uε,v)Ωε=λε(ρε;uε,v)Sε,∀v∈V(Ωε)

(2)

其中

V(Ωε)为Sobolev空间

V(Ωε)={v|v∈(H1(Ωε))N,v=0， on Γ1},

并在此空间中定义范数

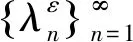
3 二阶双尺度分析

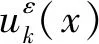
(4)

(5)

由方程组可以定义一阶校正项表达式

(7)

其中

Nα1(y)=(Nα1km(y))1≤k,m≤N∈W(Q*),

W(Q*)={vij∈(H1(Q*))N×N|vij(y)=vij(y+1),

Nα1km(y)满足单胞问题

(9)

(10)

这里|·|表示区域测度. 进一步，我们得到均匀化Steklov弹性特征值问题为

(11)

至此我们完成了均匀化过程以预测Steklov弹性特征值问题的宏观行为.

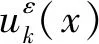
α2=1,2,...,N

(12)

其中

Nα1α2(y)=(Nα1α2km(y))1≤k,m≤N∈W(Q*).

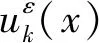
(14)

(15)

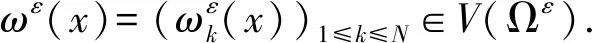
(16)

(18)

由于ωε(x)的变分形式可写成

a(ωε,v)Ωε=ελ0(ρε;u0,v)Sε

(19)

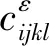
ελ0(ρε;u0,uε)Sε=λε(ρε;uε,ωε)Sε

(20)

该方程被称作“校正方程”. 将ωε(x)和uε(x),λε的展开式代入校正方程，比较方程两端ε各幂次系数得到

O(ε0):λ0(ρε;u0,u0)Sε=λ0(ρε;u0,u0)Sε，

O(ε1):λ0(ρε;u0,u1)Sε=λ0(ρε;u0,u1+ω1)Sε+

λ1(ρε;u0,u0)Sε，

O(ε2):λ0(ρε;u0,u2)Sε=λ0(ρε;u0,u2+ω2)Sε+

λ0(ρε;u1,ω1)Sε+λ1(ρε;u0,u1+ω1)Sε+

λ2(ρε;u0,u0)Sε.

(21)

这样我们有如下结果：

定理3.1令λε为满足问题的特征值.则存在与ε无关的常数C，使得

(23)

证明 首先,有

当ε足够小时，由均匀化理论有

uε(x)→u0(x),ωε(x)→u0(x).

因而ε(ρε;uε,ωε)Sε有上界. 再由Cauchy-Schwarz不等式即可得到式(23). 证毕.

定理3.2令λε为满足问题的特征值.则存在与ε无关的常数C，使得

|ε-1λε-λε,1|≤

ε3/2‖ωε-u0‖L2(ρε;Sε)+

(24)

|ε-1λε-λε,2|≤

|ε-1λε-λε,1|+ε5/2‖ωε-u0‖L2(ρε;Sε)+

(25)

证明 首先引入函数zε∈V(Ωε)为如下问题的唯一解：

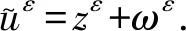
‖zε‖L2(ρε;Sε)≤C‖ε-1λεωε-λ0u0‖L2(ρε;Sε).

于是

‖zε+ωε-u0‖L2(ρε;Sε)≤

C‖ωε-u0‖L2(ρε;Sε).

因此，

ε-1λε-λε,1=

对于上面的等式右边前两项，我们分别有如下估计

Cε3/2‖ωε-u0‖L2(ρε;Sε)

(26)

对于第三项，我们有

ε3/2‖ωε-u0‖L2(ρε;Sε)]

(27)

联合不等式(26)和(27)即得估计式(24).同理也可得到式(25), 证毕.

根据估计式(23)～(25)，对特征值的误差估计转化为估计ωε与其SOTS展开式之间在L2(ρε;Sε)范数下的误差.ωε的双尺度展开是有效的，并且能够证明在范数‖·‖V(Ω)下严格收敛到u0. 假设有如下正则性：

Nα1,Nα1α2∈W(Q*)∩L2(ρ;S),

u0∈(H2(Ωε))N∩L2(ρε;Sε)，

ωε∈(H1(Ωε))N∩L2(ρε;Sε)，

我们可以得到如下估计：

最后得到如下误差估计

|ε-1λε-λ0|≤Cε,

|ε-1λε-λε,1|≤Cε2,

|ε-1λε-λε,2|≤Cε2.

4 有限元算法

基于上述二阶双尺度渐近展开模型，我们来建立关于Steklov弹性特征值问题的有限元算法.

(ii) 在单胞区域Q*上利用如下变分形式计算一阶单胞函数Nα1km(y):

(28)

(iv) 通过下面单胞区域上的变分形式解得二阶单胞函数Nα1α2km(y):

(29)

(v) 基于如下变分公式使用子空间迭代法在Ω中求解均匀化Steklov弹性特征值问题：

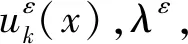
5 数值算例

对于图2所示的二维周期孔洞材料，我们考虑无量纲计算，其中非孔洞区域由单一均匀材料构成，材料杨氏模量为E=2.0e6，泊松比为ν=0.3，密度为ρ=1.0，图3给出了单胞区域Q*. 在外边界∂Ω上令uε=0，我们针对该结构内部孔洞的平面应变Steklov特征值问题进行渐近多尺度计算.

图2 ε=1/8时宏观区域ΩεFig.2 The macroscopic domain Ωε with ε=1/8

图3 单胞区域Q*Fig.3 The composite cell domain Q*

先将单胞区域、均匀化区域与周期复合区域进行三角剖分，表1显示了ε=1/8和ε=1/16时的网格信息. 在本算例中, 针对单胞问题我们采用分片线性元，均匀化问题采用分片二次元.对于原多孔区域的Steklov问题, 为减小计算开销我们也采用分片线性元. 可以看到， 当ε减小时，宏观细网格规模增大，网格尺寸减小，宏观细网格有限元计算量增加.使用双尺度有限元方法后，单胞网格和均匀化网格的单元数与结点数均保持不变，计算时间固定，当区域周期ε=1/16时，单胞个数增多，双尺度有限元法更具计算优势.

表1 网格信息Tab.1 Mesh information

在单胞区域中计算得到Nα1km(y)，进一步由材料均匀化公式计算得到均匀化密度ρ0=2.67以及均匀化本构矩阵为

设置收敛容许误差为10-10， 采用子空间迭代法计算ε=1/8与ε=1/16时模型的前6个特征值. 表2与表3列出了特征值的各阶近似解以及相对误差. 可以看到，当特征阶数增加时，我们所使用的二阶双尺度有限元方法得到的各阶近似解的相对误差也会变大. 虽然均匀化特征值和一阶校正的结果之间相差并不大，但与细网格下的特征值之间差距较大而经过二阶校正后所得到的结果

表3 ε=1/16时前6个特征值和相对误差Tab.3 The first six eigenvalues and relative errors with ε=1/16

明显好于一阶. 当ε变小的时候，所有细网格下的特征值与各阶逼近解之间的相对误差也减小.

数值算例显示，通过对各特征值近似解进行定量比较，我们可以验证二阶双尺度模型的收敛性. 由于各阶特征函数的不唯一性，这里我们只进行了简单的定性比较，也可以对求得的各阶特征函数近似解进行最小二乘逼近从而得到它们的定量比较.我们相信, 通过额外的计算二阶单胞函数，二阶近似解会具有更高的精度.

6 结 论

本文发展了周期孔洞结构的Steklov弹性特征值问题的二阶双尺度渐近分析方法，给出了特征值与对应的特征函数的SOTS渐近展开表达式，对特征值进行了误差估计，构造了相应的有限元计算方法. 数值算例结果验证了二阶双尺度分析有限元方法解决周期多孔结构模型Steklov弹性特征值问题的有效性. 我们可以得到如下结论：

(i) 均匀化解只能反映出原问题解的宏观行为，因而有必要通过一阶和二阶校正解来反映材料的微观特性，而得到的二阶逼近解显然比一阶逼近解更能捕捉到材料的局部振荡行为，所以将二阶双尺度渐近展开到二阶是合理且必要的；

(ii) 数值算例考虑了前6个特征值，当特征值变大时，使用的二阶双尺度有限元算法得到的各阶逼近解的相对误差也都变大，因而研究特征值的渐近性态对寻找适当的高阶逼近解具有重要意义；

(iii) 二阶双尺度有限元算法对于单胞问题和均匀化问题的网格划分相对来说较为粗糙，且计算时间所占内存固定，使得当ε越趋向于0时宏观区域的网格尺寸变小，计算量与内存占量变大，因此二阶双尺度方法更具计算优势.