降噪分层映射算法在多维聚类分析中的优化研究

刘 云, 张 轶, 郑文凤

(昆明理工大学信息工程与自动化学院, 昆明 650500)

1 引 言

聚类分析基于数据元素的邻近度进行类分离,根据集群内部的特征同质性将数据划分为多个子集.多维数据因其存在大量元素影响数据特征的表示,使得聚类算法的预测性能随特征复杂性的增加而降低.最新的研究表明,在多维聚类算法中引入不同的神经网络模型代替传统的初始化方案,可以分析深层特征之间的关联关系提高学习能力,提取输入数据的最佳特征属性来实现无监督的聚类任务[1,2].

Guo等[3]提出一种自编码自组织特征映射AESOM (Autoencoder-Self Organizing Mapping)算法,通过将两种非线性的降维技术集成到混合无监督的深度学习架构中,从数据中提取高度相关的低维特征,算法可以检测并减少数据噪声和缺陷的负面影响.Aly等[4]提出深度卷积自组织特征映射DCSOM (Deep Convolutional Self-Organizing Map)算法,将多个卷积自组织特征映射SOM (Self-Organizing Feature Map)层级联以创建深度网络结构,对最终卷积SOM层产生的特征空间进行计算获得有效的特征表示,但在算法中未实施适当的停止标准可能会增加计算成本.文献[5]提出平滑自组织图S-SOM(Smoothed Self-Organizing Map)算法,基于输入向量与其最接近的码本向量之间的互补指数距离提取有效特征,减少嘈杂数据中异常特征的影响提高聚类性能,但并未考虑权重对指数距离的影响.

为了从多维数据的非线性深层结构中选取有效的特征属性进行无监督聚类分析[6],本文提出一种降噪分层映射DHM (Denoised Hierarchical Mapping)算法.首先,基于降噪自动编码器DAE (Denoising Autoencoder)的非循环神经网络结构结合权重和偏置参数得到激活函数,通过激活函数的训练实现特征重构获取特征空间[7].其次,采用自组织特征映射神经网替换DEA的输出层,依据训练得到的特征空间来调整SOM,通过计算最小加权平方欧式距离来寻找获胜神经元.最后,迭代学习训练整体调节DHM算法的权重系数和偏置参数,实现有效的无监督聚类方案.仿真结果表明,对比同类算法,DHM算法在聚类准确性和鲁棒性方面有所改善.

2 降噪分层映射(DHM)模型

聚类分析的性能取决于选取数据特征的有效性,研究重点是采用有效的方法分析数据对象之间的离散性或相异性信息,选取输入数据属性表示的最佳特征用于数据分类.

2.1 DHM算法模型

良好的特征表示方法不会受到多维数据损坏和干扰的影响,引入DAE作为特征提取模块可以从混杂的输入数据中重建原始的特征表示,选取最佳特征.DAE的原理是采用部分破坏原始输入特征的方法,通过从具有噪声和波动的数据输入中重建有效的输入来强制自动编码器的隐藏层捕获输入数据的最佳特征,得到更高质量和鲁棒性的特征表示.消除噪声不是DHM模型的目标,而是通过引入损坏的过程实现特征重构,使特征提取更接近输入数据空间中存在的稳定结构和不变特征,学习更有效的特征表示[8].

无监督学习过程有助于调整深度学习方法中的神经网络参数,对多维特征空间的分布进行优化.基于上述研究,提出将输入数据空间的特征提取神经网(DAE)和输出空间的无监督学习算法(SOM)在结构上进行组合为降噪分层映射模型,如图1所示.

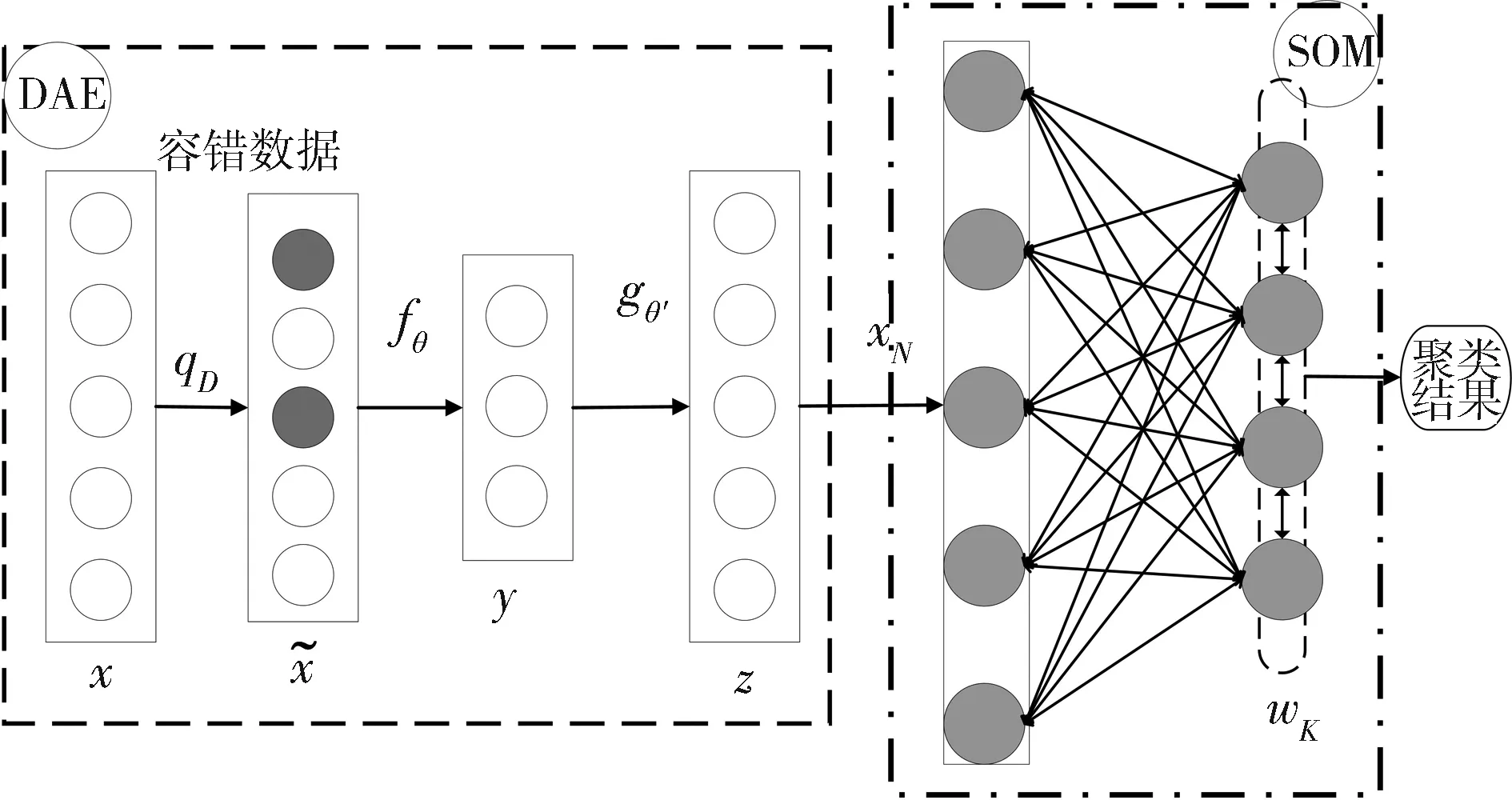
图1 DHM算法模型Fig.1 Structure of DHM

在图1中，第一阶段,容错数据通过特征选择模型的训练,基于DAE的特征选择模型通过在训练神经网络的过程中引入随机破坏行为,获取输入数据的分布特征和相关性特征,消除容错数据中破坏数据的噪声使特征选择更接近输入数据空间中的稳定结构和不变特征；第二阶段,无监督聚类模型接受特征选择神经网络的隐藏层输出,捕获并投影从特征选择中提取的特征之间的关系,并将它们同时映射到二维平面上,达到基于拓扑的聚类分析[9].

通过有效地结合降噪自动编码器和自组织映射神经网络,可以在神经网络图中显示输入特征的非线性组合的影响,并基于最有效特征来实现无监督聚类方案[3].

2.2 特征选择模型

特征选择模型DAE可用于从采样子集中选取有效的关联特征重构数据集,如图1所示[10].输入的容错数据定义如下.

(1)

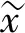
(2)

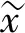
(3)

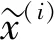
2.3 无监督聚类模型

聚类模型采用自组织特征映射(SOM)构成两层前馈神经网络如图1第二部分所示[12].左为输入层,由输入结点构成,若输入向量有N个维度则输入端共有N个神经元.右为竞争层,由K个输出神经元构成,形成一个等间距的二维神经元矩阵,每个神经元对应一个最佳匹配获胜神经元,代表了一类具有相似特征的数据点集群.所有输入神经元到输出神经元都有权值连接,竞争层的每个神经元同它周围的其他神经元侧向连接.

SOM的输入数据构成一个包含N维欧几里得向量x的序列{x(t)},其中一个整数t表示序列中的一个步骤.{mi(t)}为另一个表示连续计算的n维实向量序列的近似模型.i是与mi相关的网格节点的空间索引,原始SOM算法假定以下过程收敛并生成模型所需的有序值.

mi(t+1)=mi(t)+hci(t)[X(t)-mi(t)]

(4)

其中,hci(t)是邻域函数,下标c是网络中特定节点(获胜者)的索引,即模型mi(t)与x(t)具有最小欧几里得距离.

(5)

输入数据根据式(5)选择网络中的最佳匹配节点,根据式(4)和式(5)修改了获胜节点以及网络中其空间邻域处的模型.更新后的模型将更好地与输入匹配.在不同节点上的修改率取决于领域函数hci(t)的数学形式.

hci(t)=α(t)exp[-sqdist(c,i)/2δ2(t)]

(6)

其中,α(t)是t的单调递减的标量函数.(c,i)是网络中节点c和i之间几何距离的平方,δ(t)为另一个t的单调递减函数.为了获得足够的统计准确性,每个模型都必须更新.特别地,δ不能为零,否则将失去其排序能力.

每一个输入数据经过神经网络训练后都要对获胜神经元及其周围节点的权值进行调整以更加匹配输入权值.稳定后的网络得到与输入数据对应的特征映射空间,实现自动聚类.

3 降噪分层映射(DHM)算法

DHM模型在统一的体系结构中结合了输入数据空间的特征选择神经网路模型和输出空间自组织特征映射的聚类模型,如图2所示.

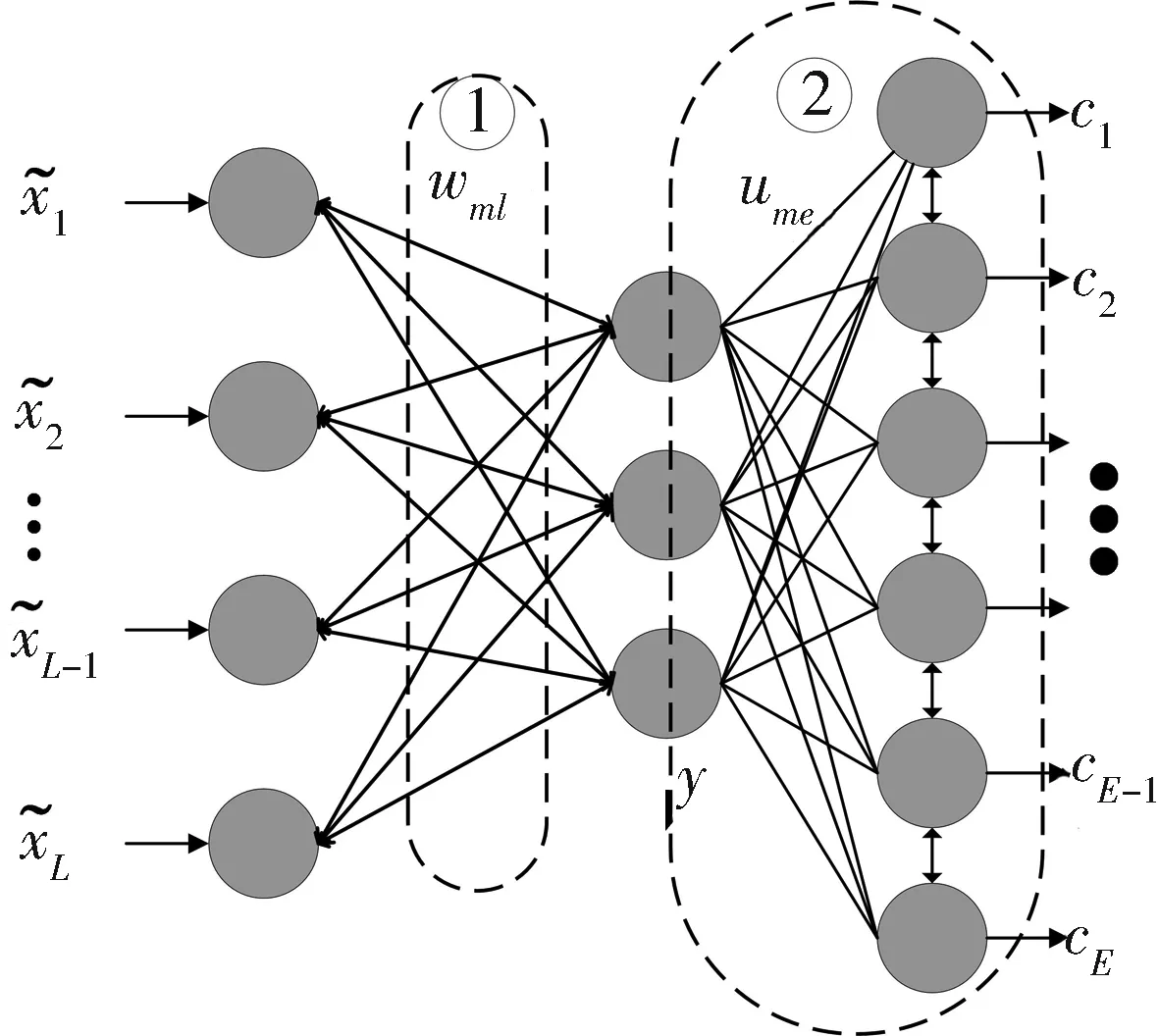
图2 DHM算法网络结构Fig.2 DHM algorithm network structure

在图2中，算法的学习过程分为两个阶段,第一阶段,构建DAE神经网络训练得到有效的输入特征空间[13]；在第二阶段,DAE的隐藏层编码应用于SOM的输入,SOM使用这些分布式特征进行参数调整,实现无监督聚类目标.

3.1 DHM算法学习

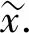
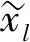
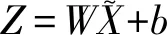
(7)

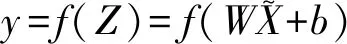
(8)

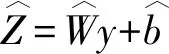
(9)

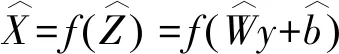
(10)

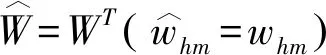
(11)

这是用于实值输入的平方误差函数,对于二进制或X∈[0,1]L情况,输入交叉熵损失函数代替.更新网络参数采用梯度下降方法,以最大程度地减少重构误差,步骤如下.

(12)

(13)

(14)

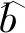
3.1.2 第二阶段学习 如图2所示,考虑到拓扑上的低维有序神经元,E为SOM神经网络的竞争层神经元总数.每个神经元e与SOM的可调参数码本矢量ue相互关联,可以看作点ume属于每个单独隐藏层ym的分布表示,码本矢量可以排列成矩阵UM×E.

在第二阶段,训练算法运用梯度下降在建模任务中寻求最小值,将成本函数[14]定义为

(15)

其中,hde是邻域函数,它的宽度和形状控制表面的弹性神经元.K引入一个加权平均过程表示每个码本矢量和给定隐藏层间的距离.权重系数的作用是加强一些规则的限制,成本函数可以相应表示为

(16)

(17)

其中,hce为神经元在晶格上的几何坐标,对于有限的输入样本集,成本函数是连续的,用于最小化成本函数的梯度下降步骤定义为

W(next)=W-η∇WK(W,b,U)

(18)

b(next)=b-η∇bK(W,b,U)

(19)

U(next)=U-θ∇UK(W,b,U)

(20)

其中,θ和η是标量学习率因子,学习率η调整权重,偏差应该传递比学习率θ低的值来调整映射.因此,在第二阶段开始时,η和θ必须至少相差一个数量级以缓和训练失衡.

3.2 DHM算法实现

算法在第一阶段学习产生非线性空间,在第二阶段期间使用不同的优化目标进一步完善特征选择.因为无法评估用于无监督学习的表示空间学习阶段之间的比例平衡无法精确调整.为了解决两阶段交错训练的问题,首先由式(12)～(14)调整DEA的参数并表示特征空间.再根据上一阶段固定和不变的表示空间式(20)来调整SOM,然后进行所有模型参数的组合并行微调.最后由式(18)～(20)对模型进行训练,从而生成一个更加有效的特征选择模型,避免了表示空间的广泛失真,有利于神经映射.

更新DHM参数的过程的每个特定步骤如下,第一阶段的迭代参数表示为

1≤i≤M,1≤j≤L

(21)

1≤i≤M

(22)

(23)

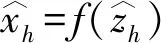
(24)

1≤i≤M,1≤j≤L

(25)

1≤i≤M

(26)

1≤i≤M,1≤e≤E

(27)

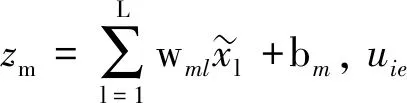
(28)

(29)

最后,如果单峰邻域函数的半径足够窄,几乎可以涵盖最接近的领域,那么先前检测到的最佳匹配神经元将与SOM的获胜者神经元重合.

(30)

只要适用邻域大小条件两个表达式可以互换使用.基于以上分析,迭代算法解决无监督学习问题的伪代码如算法1所示.

在此方法的每个步骤中,所有变量均根据其相应公式进行更新,此过程迭代进行,直到变量收敛为止.

3.3 DHM算法分析及评价

为了验证所提出的算法,内部和外部评估标准共同构成了算法评价体系[15].外部聚类标准包含标准化互信息,聚类纯度.标准化互信息要求定义一些额外的数量a,sp代表集群类别中第p组的样本数,st代表现有分类第t类的样本数.sp,t表示同时出现在第p分区和第t类别的样本数.

NMI=

(31)

NMI的值域为[0,1],较低的值表示较高的不确定性.纯度是聚类分析中广泛使用的外部度量.

(32)

聚类性能的内部度量包含均方量化误差和DB度量[14].量化误差通过以下各项来确定网络对输入和表示的适应性.

(33)

DB度量表示最接近簇之间的成对相似度平均值的估计值.

(34)

其中,CDi是集群i的离散度.MDij是集群i和j的码本向量值在[0,+∞]范围内,较高的离散度和相似群集之间的距离较大得到较高的DB值,反应了群集和神经映射的欠佳.

(35)

(36)

其中,Si是集群i的样本数；ui是相同集群的质心.当r=2且q=1时,MDij是质心和CDi之间的欧氏距离.

4 仿真分析

4.1 仿真环境和方法

为了验证算法的多维聚类性能,选用UCI Machine Learning Repositor中多维数据集手写数字的光学识别Optdigits[16]评估DHM算法解决实际问题的能力.表1为仿真数据集信息,仿真环境为:python 3.7;Win10 64位操作系统;2.6 GHz CPU；8 G内存.

表1 数据集信息Tab.1 Data set information

为了验证所提出的算法,实验基于Optdigits数据集,交替固定隐藏层神经元数量和噪声类型与参数,观察相对变量变化下的聚类性能.

4.2 外部聚类性能影响分析

为了研究算法外部聚类性能,在Optidigits数据集中评估DHM算法与AESOM,DCSOM和S-SOM算法在固定噪声参数研究隐藏层神经元数量变化对外部聚类性能的影响,以及固定隐藏层神经元数量研究不同噪声参数类型变化下的外部聚类评价指标结果.仿真均取20次重复实验的平均值,结果如图3和图4所示.

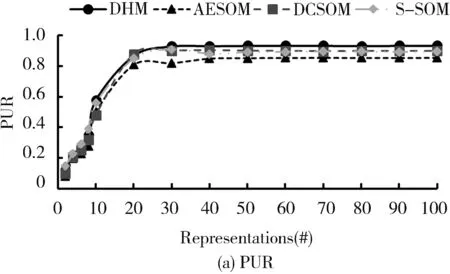
图3 算法外部聚类指标对比，高斯噪声的标准偏差保持恒定且等于0.5Fig.3 Algorithm external clustering index comparison, with Gaussian noise’s standard deviation kept constant and equal to 0.5

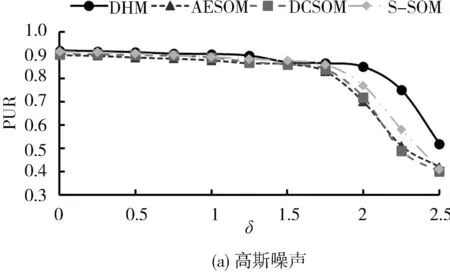
图4 具有32个隐藏层神经元的算法外部聚类指标对比Fig.4 Comparison of external clustering indicators of algorithms with 32 hidden neurons

从图3可以观察到,固定高斯噪声的标准偏差为0.5的情况下,4种算法的整体趋势随着隐藏层神经元数量的提高拥有更高的聚类精度.同对比算法相比DHM算法在外部聚类评价指标PUR和NMI上性能差异较小,但当隐藏层表示为10#～20#时,DMH和S-SOM算法的外部聚类性能提升同AESOM和DCSOM算法相比较为明显,但随着隐藏层神经元数量的增加,DHM算法具有更高的聚类精度.

从图4a和4b可以观察到,当神经元数量固定为32的情况下,随着高斯噪声标准偏差的增大,4种算法的外部聚类性能.

当噪声失真在0～1.5δ时,4种算法的PUR和NMI性能指标没有显著差异.但当高斯噪声在1.5δ～2.5δ时,同对比算法相比DHM算法在噪声外部聚类评价指标PUR和NMI上性能更为优异,且随着噪声失真的变大,DHM算法能够应对更严重的噪声失真提供更高的聚类精度.另一方面,从图4c和4d可以观察到,当掩蔽噪声的破坏百分比在0%～80%情况下,4种算法的PUR和NMI指标性能差异较小,显示了4种算法均有较强的抗噪性能.但当掩蔽噪声破坏百分比达到90%～100%时,DHM算法同对比算法相比显示出了更高的聚类精度.

交替固定参数仿真结果表明,DHM算法在SOM模型中引入降噪组件实现特征重构,插入经过调参的隐藏层神经元对聚类分析提供了更优异的性能,同对比算法相比在交替固定隐藏层表示和噪声参数情况下均能表现出更高的聚类精度和抗噪鲁棒性.

4.3 内部聚类性能影响分析

为了研究算法的内部聚类性能,在Optidigits数据集中评估DHM算法与AESOM,DCSOM和S-SOM算法的内部聚类评价指标结果.仿真均取20次重复实验的平均值,结果如图5和图6所示.

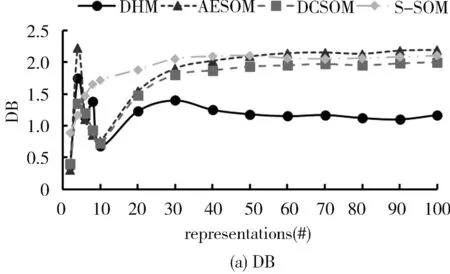
图5 算法内部聚类指标对比，高斯噪声的标准偏差保持恒定且等于0.5Fig.5 Algorithm internal clustering index comparison, with Gaussian noise’s standard deviation kept constant and equal to 0.5

从图5可以观察到,固定高斯噪声的标准偏差为0.5的情况下,相较对比算法DHM算法在内部聚类评价指标DB和QE上性能更为优异.随着隐藏层表示的增大,四种算法的内部聚类指标总体趋势为在0#～40#的隐藏层表示阶段变化上升,在40#～100#阶段逐渐达到平稳,S-SOM算法的DB和QE性能均较快达到平稳,分析是由于权重对指数距离的影响使得集群分离性和紧凑型较差更小的DB和QE值显示出DHM算法更好的集群分离性和紧凑性.

从图6a和6b可以观察到,当神经元数量为32个的情况下,在高斯噪声失真的整个变化过程中,不论是DB指标还是QE指标,DHM同对比算法相比均表现出更小值,显示出算法更好的集群分离性.从图6c和6d可以观察到,当神经元数量为32个的情况下,随着掩蔽噪声破坏百分比的增加,在0%～80%阶段4种算法的DB和QE指标均呈现缓慢的平稳降低状态,在80%～100%下出现波动变化后快速降低的情况.DHM算法在掩蔽噪声变化的整个过程中,均有更低的DB和QE值,DHM算法明显改善了集群组织的可分离性,具有更好的内部聚类性能.

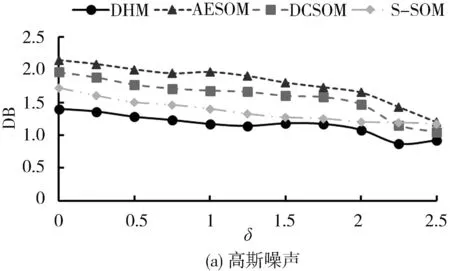
图6 具有32个隐藏层神经元的算法内部聚类指标对比Fig.6 Comparison of internal clustering indicators of algorithms with 32 hidden neurons

结合两次仿真实验,DHM算法的输入特征空间的隐藏层表示更加紧凑,保留了原始数据关联特征实现良好的集群可分离性,具有更高的聚类准确性和神经网络拟合性.在基准数据集线圈和耶鲁人脸数据库的仿真实验也同样验证了DHM算法的聚类准确性和有效性[17].

5 结 论

采用深度神经网络学习训练,可以选取有效的特征属性表征数据间的关联信息进行无监督聚类分析,本文研究提出一种降噪分层映射算法(DHM).首先,基于降噪自动编码器的神经网络从原始数据中学习训练得到激活函数特征空间实现特征重构.其次,特征空间用于训练自组织特征映射神经网,通过计算最小加权平方欧式距离来寻找最佳匹配获胜神经元.最后,结合已调组件进行共同训练,优化权重系数和偏置参数,实现有效的多维聚类分析.仿真结果同对比算法相比,DHM算法在聚类精确性和有效性方面均有提升.下一步,面对更为复杂的数据结构和分析需求,将研究更有效深度学习方法.